垂直隔板开孔率对液体晃荡影响的试验
2022-03-29薛米安彭天成朱爱蒙郑金海苑晓丽
薛米安,彭天成,朱爱蒙,郑金海,苑晓丽
(1.河海大学海岸灾害及防护教育部重点实验室,江苏 南京 210098;2.河海大学港口海岸与近海工程学院,江苏 南京 210098; 3.河海大学理学院,江苏 南京 210098)
液体晃荡水动力学是船舶与海洋工程学科领域的重要研究方向,是液货船舶、航空航天和陆上储液结构优化设计和安全运行的关键性控制因素。长时间剧烈的液体晃荡不但会引起大型液舱结构疲劳损伤,还会导致载液舱船舶重心不稳而发生液货运输船倾覆事故。因此研究如何抑制储液结构内的液体晃荡,减小其内部液体晃荡波高及冲击压强,具有十分重要的意义。在液舱内安装隔板是一种有效抑制液体晃荡的方法[1-2]。Armenio等[3]通过数值模拟研究了垂直隔板对液舱晃荡的衰减效果,发现在液舱底部中间位置安装垂直隔板能有效抑制液体晃荡;Liu等[4]通过数值模拟研究了在二维和三维矩形液舱中安装垂直隔板对晃荡的影响;Akyildiz[5]通过改变垂直隔板的高度与初始水深比,研究了隔板高度对减晃效果的影响;Chu等[6]通过物理模型试验和大涡模拟模型研究了液舱底部装有多个垂直隔板的减晃效果;Qin等[7]通过数值模拟研究了垂直隔板的高度和水平隔板的长度对减晃效果的影响;Ünal等[8]研究了T形隔板的减晃效果,当T形隔板的高度大于80%水深时,隔板抑制冲击压强和晃荡波高的效果很显著;朱小松等[9]通过数值模拟对比了垂直隔板和T形隔板的减晃效果,结果表明垂直隔板和T形隔板在隔板高度为水深60%~80%时具有很好的减晃效果,对于T形隔板,上部宽度越宽减晃效果越好;Yu等[10-11]通过物理模型试验研究了低载液率下格栅型隔板的减晃效果;Xue等[12]利用自主开发的数值水池模型NEWTANK模拟研究了环形隔板对液体晃荡的抑制效果并揭示了隔板的减晃机制。
研究发现因涡致减阻机制,开孔隔板的减晃效果优于无孔隔板。Gao等[13]研究了开孔隔板的高度、数量、位置、多孔效应参数等对液体晃荡的影响;Nasar等[14]研究了多孔隔板的减晃效果,并考虑了15.0%、20.2%和25.2% 3种不同孔隙率对隔板减晃效果的影响。金恒等[15]建立了带水平开孔隔板晃荡的势流理论分析模型,研究了开孔隔板淹没深度和开孔率对液舱共振频率和晃荡波高的影响规律。Xue等[16]通过物理模型试验和数值模拟研究了方形开孔隔板的减晃效果,并对比分析了开孔位置对隔板减晃效果的影响。Younes等[17]试验研究了不同开孔数量的垂直隔板对于压强及自由液面的影响;Molin等[18]试验验研究了不同频率和振幅下开孔隔板对液体晃荡的影响,并采用线性势流理论建立了较为准确的数值模型;Cassolato等[19]研究了带不同倾斜角度的开孔隔板对液舱水动力学特性的影响,并开发模型用于预测晃荡过程的能量损耗。涂娇阳等[20]采用VOF追踪自由液面方法和动网格技术建立三维矩形液舱晃荡数值模型探究了条形孔对晃荡压力的影响。刘谋斌等[21]对带有隔板的棱形液舱进行了SPH模拟,发现适当改变箱体结构也可以有效抑制晃荡现象。Xue等[22]研究了包括开孔隔板在内的不同结构垂直隔板对晃荡压强分布的影响规律,研究发现垂直隔板开孔后能够更有效地抑制液体晃荡。
为进一步研究无孔隔板和开孔隔板对减小液体晃荡效果的差异,明确开孔率大小对液体晃荡特性的影响规律,本文通过改变隔板的开孔半径来改变开孔隔板开孔率的大小,探索不同开孔率隔板对液体晃荡波高和压强大小的衰减作用。
1 试验装置
1.1 运动平台与试验模型
图1为试验采用的六自由度运动模拟平台,平台可以进行单自由度或任意自由度的耦合运动,台面尺寸为1.5 m×1.5 m,能够负载9.8 kN。通过采用高频运动幅度衰减补偿技术,该平台的运动频率最大可达10 Hz。通过在控制软件中输入平台的运动幅度、频率等参数,可以实现运动平台的六自由度简谐运动或随机运动。

图1 试验平台 Fig.1 Experimental platform
试验液舱模型由液舱和隔板两部分组成,隔板垂直固定在液舱底部中间位置,矩形液舱由有机玻璃制作,内部尺寸为长600 mm、宽300 mm、高650 mm。液舱固定在运动平台上的中间位置,液舱模型舱壁的厚度为10 mm,可以假定为刚性结构。试验研究的垂直隔板分别为无孔隔板及开孔率ε=0.1的开孔隔板,隔板均为有机玻璃制作,厚6 mm、宽300 mm、高206 mm。开孔隔板的开孔数目为28,开孔半径8.4 mm。无孔隔板及开孔隔板模型尺寸如图2所示。开孔隔板的开孔率ε定义如下:
(1)
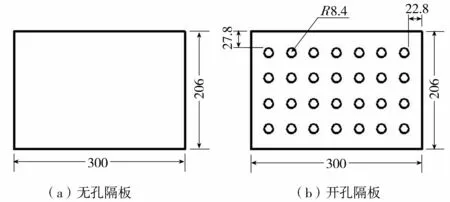
图2 隔板尺寸(单位:mm) Fig.2 Sizes of baffles(unit:mm)
式中:n为隔板的开孔数量;s为隔板的面积;r为开孔半径。
本研究主要聚焦矩形液舱内有限水深条件下安装隔板对液体晃荡的抑制效果,因此液舱内水深h取258 mm。在液舱两侧距离壁面20 mm处分别安装了1支波高仪,以测量波高随着晃荡过程的时程曲线;在矩形液舱长度方向左侧舱壁中心线上安装了5支微型数字压力传感器,压力传感器离液舱底部的距离分别为30 mm、70 mm、110 mm、150 mm和190 mm,5支压力传感器自下而上依次命名为P1、P2、P3、P4和P5,如图3所示。每次试验前均对试验平台、波高仪、压力传感器等进行率定,以确保试验结果的准确性。
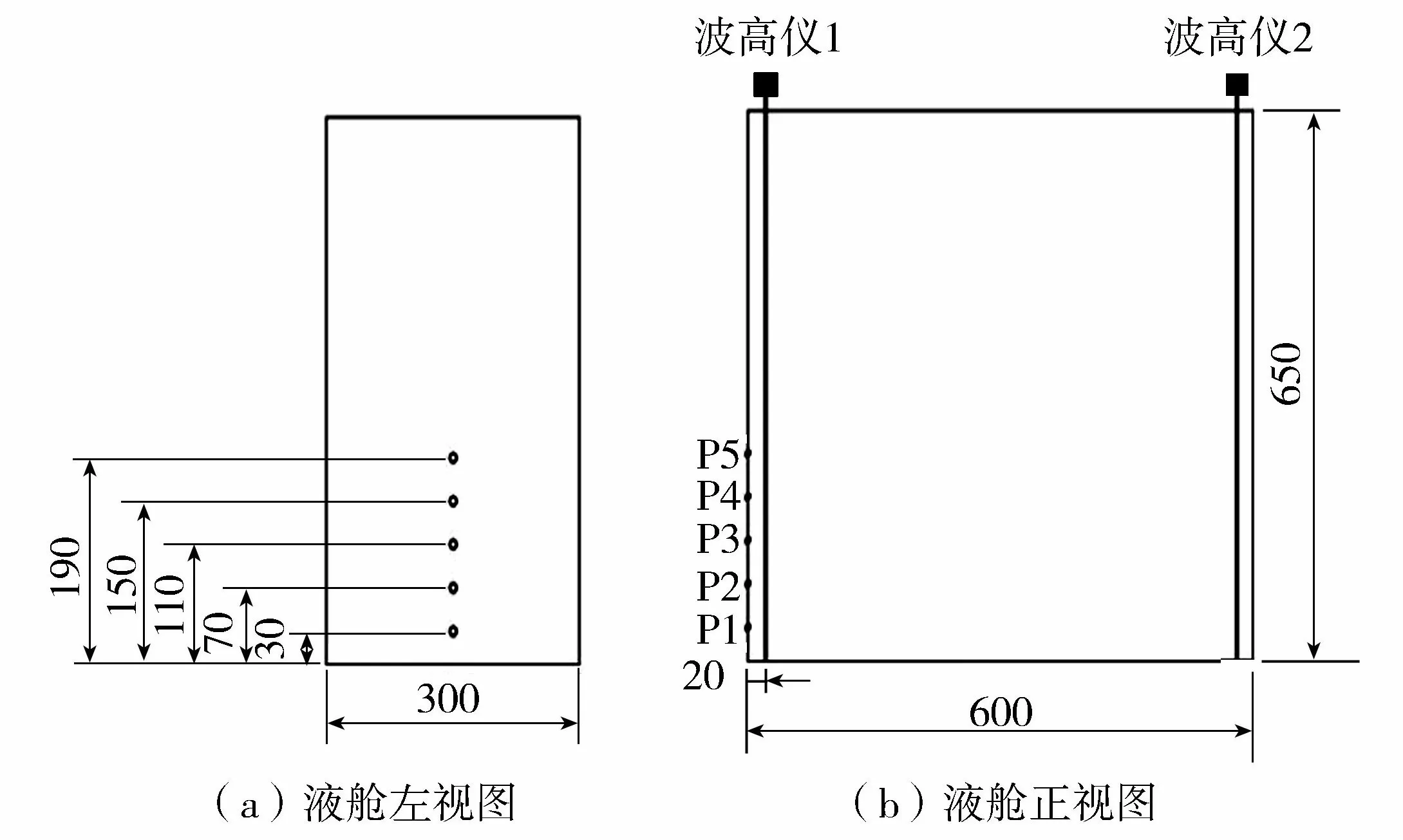
图3 波高仪及压力测点位置示意图(单位:mm)Fig.3 Layout of measure points of wave probes and pressure sensors (unit: mm)
1.2 试验描述
试验中平台按正弦函数运动,以驱动液舱内液体产生受迫晃荡。运动位移函数为
x=Asin(2πft)
(2)
式中:A为平动幅值,取2 mm;f为外激励频率;t为运动时间。
安装不同隔板后的液舱固有频率用fn表示,给液舱施加一个初始扰动,液舱内液体将发生自由晃荡运动,然后对液舱内液体晃荡波高时程曲线进行快速傅里叶变换(FFT),可以得到安装无孔隔板后的液舱固有频率为f0=0.80 Hz,安装开孔隔板的液舱固有频率为f1=0.96 Hz。安装无孔隔板后的液舱系统固有频率可以由下式计算

(3)
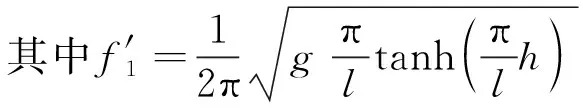
(4)
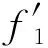
2 两种隔板的减晃效果分析
2.1 对最大晃荡波高的影响
图4(a)为安装无孔隔板和开孔隔板的液舱在水平运动下,液舱内液体最大晃荡波高(2支波高仪测得最大晃荡波高的平均值)对外激励频率的响应曲线(图中Hmax为最大晃荡波高)。由于无孔隔板和开孔隔板对应的液舱固有频率不同,液舱内液体最大晃荡波高所对应的外激励频率f也不同。最大晃荡波高先随着外激励频率的增大而增大,在f=f0处,无孔隔板的最大晃荡波高(指安装隔板后液舱内的最大晃荡波高)突然增大并达到最大值,其值约为同频率下开孔隔板最大晃荡波高的3倍。随着外激励频率的逐渐增大,无孔隔板的最大晃荡波高逐渐减小,开孔隔板的最大晃荡波高持续增大,在外激励频率f=f1处达到最大值,此时无孔隔板的最大晃荡波高小于开孔隔板的最大晃荡波高,随后开孔隔板的最大晃荡波高随着外激励频率的增大而逐渐减小。由最大晃荡波高的频率响应曲线可以看出,开孔隔板的最大晃荡波高变化曲线与无孔隔板的最大晃荡波高变化曲线相比变化幅度较小,且开孔隔板在其固有频率下的最大晃荡波高值小于无孔隔板在其固有频率下的最大晃荡波高值。

图4 不同隔板最大晃荡波高和最大冲击压强对外激励频率的响应曲线Fig.4 Frequency response curve of maximum sloshing wave height and maximum impact pressure under different kinds of baffles
图5和图6分别为无孔隔板和开孔隔板在固有频率激励下液舱内液体晃荡时前30 s的波高时程曲线和Morlet小波能谱图(图5中η为液舱内液体晃荡波高; 图6能谱强度为无量纲值,与时程曲线对应时刻的幅值相关)。由图5(a)的波高时程曲线可以看出,无孔隔板的晃荡波高随着时间的增长呈逐渐增大的趋势,在8 s左右出现了明显的高频次波,且随着时间的增长,高频次波的幅值也在不断增大。结合FFT分析和Morlet小波能谱(图6(a))可以看出,无孔隔板在f=f0时,晃荡波的频率成分除了外激励频率外还存在其倍频,且其主要由外激励频率f0及2f0组成。根据Morlet小波能谱,2f0在5 s左右开始出现,且随着时间的增长,波幅值也逐渐增大,对应了波高时程曲线中出现的高频次波。从图5(b)可以看出,安装开孔隔板后,晃荡波高在较短的时间内达到一定值后趋于稳定,达到稳态。由FFT分析和Morlet小波能谱(图6(b))可以看出,安装开孔隔板后,当f=f1时,液舱内液体晃荡波频率成分主要是外激励频率f1。从隔板对自由液面晃荡波高抑制效果来看,开孔隔板抑制晃荡波高的效果要优于无孔隔板。
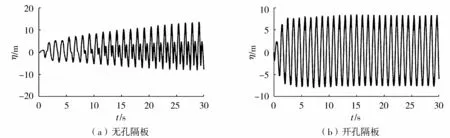
图5 固有频率激励下不同隔板的晃荡波高时程曲线Fig.5 Time history of sloshing wave height under resonant frequencies with different baffles

图6 固有频率激励下不同隔板晃荡波高对应的Morlet小波能谱Fig.6 Morlet wavelet energy spectrum of sloshing wave height with different baffles under resonant frequencies
2.2 对晃荡冲击压强的影响
为了进一步对比分析无孔隔板与开孔隔板的减晃作用,研究了不同位置处压力传感器测得的前30 s最大冲击压强Pmax对外激励频率的响应关系,结果如图4(b) ~(f)所示。与最大晃荡波高频率响应曲线相同,不同位置处,最大冲击压强均是先随着外激励频率的增大而增大,当外激励频率为固有频率时,最大冲击压强达到最大值,随后随着频率的增大而逐渐减小。在P1、P2、P4这3个位置处,开孔隔板固有频率下的最大冲击压强大于无孔隔板固有频率下的最大冲击压强,而在P3、P5两个位置处,无孔隔板固有频率下的最大冲击压强大于开孔隔板固有频率下的最大冲击压强。可以得出隔板抑制晃荡波对液舱壁的冲击压强效果除了与隔板的种类有关外,还与压力测点的相对位置有关;结合隔板抑制液舱内液体晃荡波高的效果来看,开孔隔板比无孔隔板在抑制液舱晃荡上有较为明显的优势。
3 开孔率对晃荡特性的影响
3.1 开孔率对隔板减晃效果的影响
为了研究开孔隔板的开孔率对液舱晃荡的减晃效果,控制隔板开孔数保持不变,通过调整隔板的开孔半径,来改变隔板的开孔率。改变后的开孔率ε分别为0.2、0.3和0.4,即对应的开孔半径为11.85 mm、14.50 mm和16.67 mm,如图7所示。给液舱施加初始扰动,采集晃荡波高随时间的变化值,经过FFT分析,得到对应开孔率隔板在258 mm水深下的固有频率分别为f2=1.02、f3=1.03、f4=1.05。

图7 不同开孔率隔板的尺寸(单位:mm)Fig.7 Sizes of baffles with different perforation rates(unit: mm)
图8为不同隔板开孔率下最大晃荡波高和不同位置处晃荡最大冲击压强对外激励频率的响应曲线。不论是最大晃荡波高还是晃荡时的最大冲击压强对外激励频率的响应曲线,不同开孔率隔板呈现出相同的变化趋势,即最大晃荡波高和最大冲击压强均随着外激励频率的增大逐渐增大,当外激励频率为固有频率时最大晃荡波高和最大冲击压强达到最大值,之后随着外激励频率的增大而逐渐减小。在开孔率ε为0.1~0.4范围内,随着开孔半径即开孔率的增大,最大晃荡波高和晃荡最大冲击压强也逐渐增大。此外,由图8可知,随着开孔率的增大,与最大晃荡波高或最大冲击压强相对应的响应频率也逐渐增大,表明液舱系统的固有频率与隔板开孔率密切相关。

图8 不同开孔率隔板最大晃荡波高和最大冲击压强对外激励频率的响应曲线Fig.8 Frequency response curve of maximum sloshing wave height and maximum impact pressure under external excitation with baffles of different perforation rates
3.2 开孔率对晃荡波高时程曲线的影响
图9和图10分别为0.8倍、1.0倍、1.2倍固有频率激励下,安装不同开孔率隔板后晃荡波高时程曲线和相应的Morlet小波能谱图。由图9(a)~(d)和图10(a)~(d)可以看出,外激励频率为0.8倍固有频率时,晃荡波的频率成分除了外激励频率,还存在固有频率,且随着开孔率的逐渐增大,固有频率激励下所对应的晃荡波高幅度也逐渐增大。从Morlet小波能谱图可以看出,波能在前5 s处达到最大,而后波能慢慢减小并趋于稳定。此外,随着隔板开孔率的增大,波能逐渐出现周期性变化,当开孔率为0.4时,波能的聚集出现了明显的周期性变化,与波高时程曲线中出现的波形的周期性变化相对应。
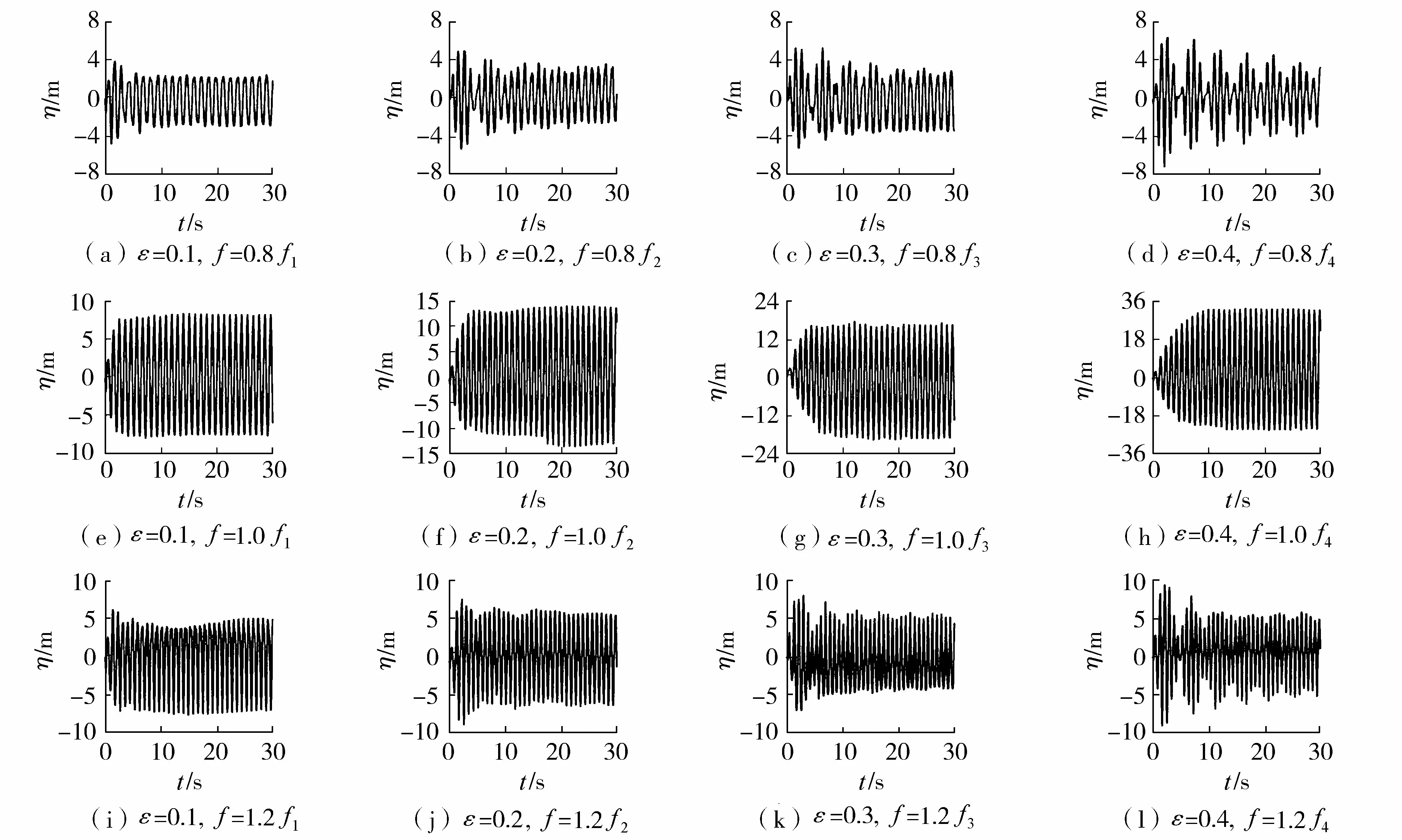
图9 不同固有频率激励下不同开孔率隔板所对应的晃荡波高时程曲线Fig.9 Time history of wave height under different natural frequencies with baffles of different perforation rates
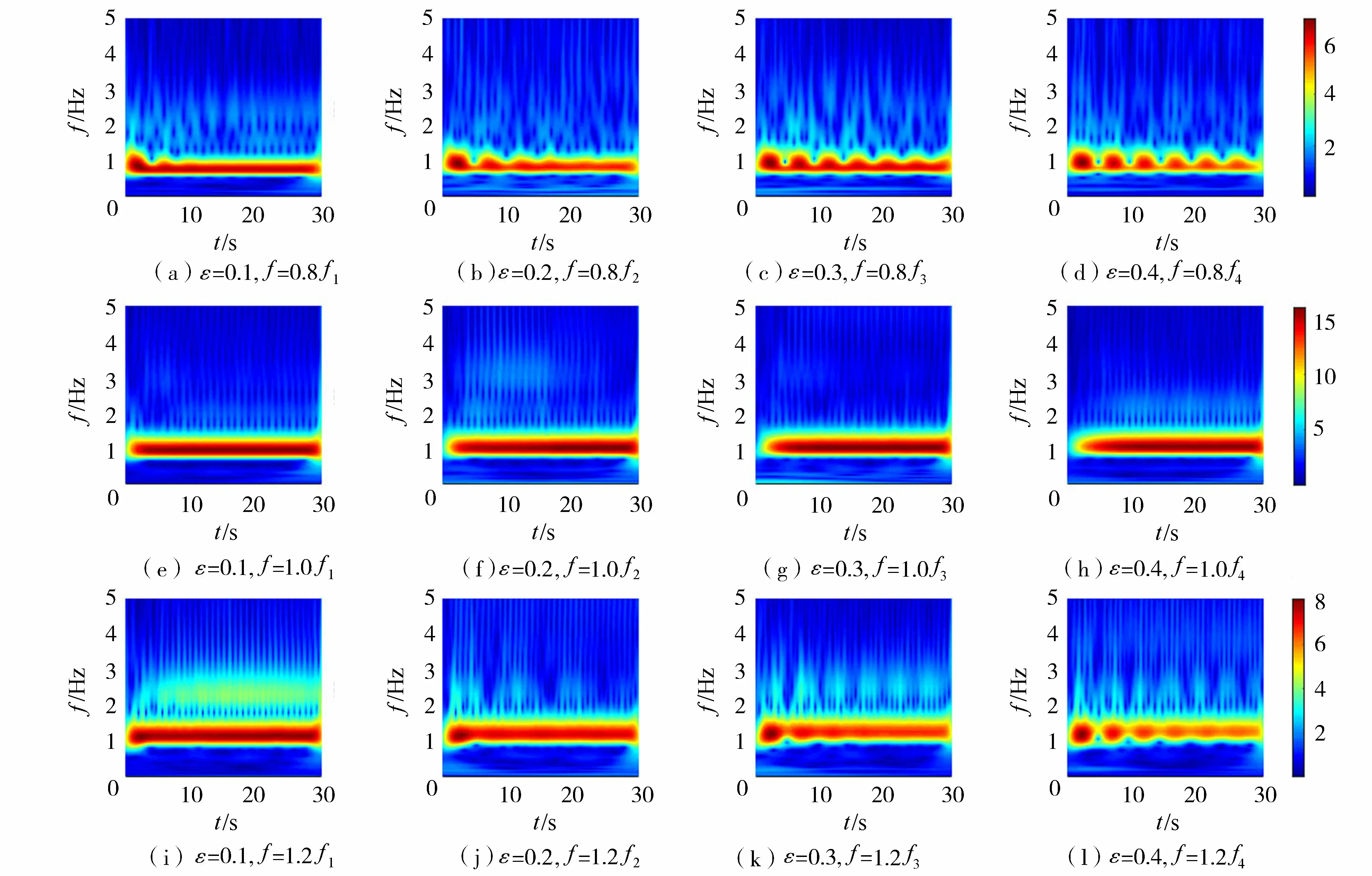
图10 不同固有频率激励下不同开孔率隔板晃荡波高的Morlet小波能谱Fig.10 Morlet wavelet energy spectrum curves of sloshing wave height under different natural frequencies with baffles of different perforation rates
由图9(e)~(h)和图10(e)~(h)可以看出,当外激励频率为固有频率时,不同开孔率隔板的波高时程曲线相似,波高先是随着时间的逐渐增加而增大,增长至一定值后趋于稳定,达到稳态,然而随着开孔率的增大,波高达到稳态所需要的时间也不断增加。由FFT分析和Morlet小波能谱可知,外激励频率为固有频率时,安装不同开孔率隔板后晃荡波的频率组成成分主要为外激励频率,且随着隔板开孔率的增加,相应的幅值也不断增大。从Morlet小波能谱中也可以看出,随着隔板开孔率的增大,波能达到最大值所需要的时间也逐渐增加,这与波高时程曲线相对应。
由图9(i)~(l)和图10(i)~(l)可以看出,当隔板开孔率为0.1时,晃荡波的频率成分除了有外激励频率还有其倍频。由Morlet小波能谱知,在5 s左右开始出现能量的叠加,对应小波能谱图,此处出现的频率为2.0f,在波高时程曲线图中也可以看出在5 s左右出现了双峰现象。从图10(j)~(l))可以看出,随着隔板开孔率的增加,外激励频率倍频的影响逐渐减弱,而固有频率的影响逐渐增强,在图10(l)的小波能谱中可以看到明显的固有频率存在。此外,波能在前5 s达到最大,随后慢慢减小并趋于稳定。随着隔板开孔率的增大,波能在不同频域上的分布和传递逐渐呈现周期性变化,当开孔率为0.4时,波能的聚集出现了明显的周期性变化,与波高时程曲线中出现的波形的周期性变化相对应。
4 结 论
a.开孔隔板抑制最大晃荡波高的效果明显优于无孔隔板,无孔隔板和开孔隔板抑制液舱壁面受到的冲击压强的效果与压力测点的位置相关。
b.在开孔率为0.1~0.4的范围内,最大晃荡波高和最大冲击压强随着开孔率的增大而增大,即开孔率越小的隔板抑制晃荡产生的最大晃荡波高和最大冲击压强的效果越好。
c.外激励频率为固有频率时,安装不同开孔率隔板后所对应的晃荡波的频率主要成分为外激励频率,即其对应的固有频率。晃荡波高先是随着时间的增加而增大,增大到一定值后趋于稳定,达到稳态。随着开孔率的增大,晃荡波高达到稳态所需要的时间也逐渐增加。
d.外激励频率为0.8倍固有频率或1.2倍固有频率时,开孔率为0.1的开孔隔板所对应晃荡波的频率成分除了外激励频率,还有其倍频。随着开孔率的增大,外激励频率的倍频逐渐消失,固有频率逐渐出现,幅度也逐渐增大,波能及波高时程曲线也出现更为明显的周期性现象。
