基于纳维-斯托克斯动力学理论的高速电梯轿厢气压数值分析*

苏万斌 江叶峰 陈启锐 易灿灿

1嘉兴市特种设备检验检测院 嘉兴 314000 2武汉科技大学 武汉 430081

0 引言

随着城市化、工业化进程的不断发展，城市中高层建筑数量不断增多，人口更加密集，为了能更加有效地提高空间利用效率，高层、超高层建筑在现代生活中越来越普遍[1]。截至2020年底，全国在用电梯总数已突破800万台，同比增长12.72%。高层建筑的不断涌现对电梯提出了高扬程的客观需求，高速电梯的市场需求日益扩大，预计到2022年，我国高速电梯需求量将达到5.13万台[2，3]，但目前国内关于高速电梯的检验仍然采用普通电梯的标准，高速电梯相应的技术规范和检测手段并不成熟，开展与高速电梯相关的检测和评估技术研究对我国电梯行业的发展具有重要影响[4]。

电梯速度的不断提升之也带动了人们对电梯品质的不断追求，但由于高速电梯的柔性结构，相对于普通电梯，高速电梯不仅在运行速度上面有所提高，更会在电梯高速的运行过程中表现出更复杂的动态特性，如更为复杂的时变耦合特性，更显著的水平振动特性，受外部因素引起的激励更加敏感，电梯的寿命相比普通电梯更短[5]。电梯井道是一个封闭的长方体腔体，它由井道底部地板、井道四壁面以及井道顶天花板围组而成，中央空腔即是电梯轿厢和对重架运行的空间。一般情况下，电梯井道除井道顶配有通向机房用于穿过悬挂钢丝绳、电缆等的开孔外，不再有其他的开孔。这对于轿厢运行速度并不大的中低速电梯而言，井道中空气流动速度并不会产生不良的影响。但是对于高速电梯，特别是电梯速度超过4.0 m/s时，产生的活塞效应明显，气流速度和流线将在轿厢周围发生急剧的变化。气流的扰动严重还会使轿厢产生随机的晃动，同时会伴随着气流声音，这使轿厢内的乘客心理上产生恐惧不安。轿厢迎风面造成的气体阻力还会导致电梯驱动系统的动力的增加，降低电梯系统的效率[6]。电梯轿厢的特殊性致使其很难实现完全密封，轿厢在井道内高速运行的同时受井道气压改变、通风口的气体交换等因素，轿厢内的气压也会随之变化，导致乘坐超高速电梯的乘客基本都会存在不同程度的耳鸣现象，其中成年人居多，儿童则效果稍轻，这不仅给乘客的舒适感造成很大影响，而且长时间乘坐高速电梯甚至会使乘客耳膜破裂并引发各种心血管疾病。高速电梯轿厢气压的平衡是非常重要的[7]。

查阅相关文献，张利春等[8]对高速电梯轿厢内气压调节提出了一种新模型，但目前仍缺少实验验证；郭天水等[9]在分析了高速电梯的振动对电梯的寿命影响，但没有针对轿厢内的气压分析。刘志仁等[10]对电梯井道空气流动做了二维分析，较好地解释了井道内气流的运动变化，但是二维分析存在局限，不能很好地在实际三维空间内体现。由于目前对高速电梯运行环境气压的研究多是以电梯井道为主，对电梯轿厢内的气压检测寥寥无几，部分研究存在局限和不足。本文比较了3种轿厢排气孔分布，采用流体模拟和三维仿真的方法对高速电梯运行时的轿厢内气流的运动过程进行分析，利用改进的纳维-斯托克斯理论方程，结合湍流模型中的大涡模型，用盒式滤波器把大涡模型分成大小涡运动分别求解，最后应用到理想气体方程中，得出高速电梯轿厢内部气压变化的k-ε方程，并通过实测数据，比较得到轿厢内气压的变化规律，为平衡轿厢内的气压提供一种新的检测方法，减轻乘客耳鸣现象，提升电梯乘坐舒适度。

1 轿厢通气孔分布

目前，高层建筑设计往往采用剪力端的核心简结构设计施工电梯井道，这样的设计要求井道壁承受相当大的载荷，井道壁的开口要尽量小。在电梯安装时，为了保证电梯运行时在噪声、振动等方面达到良好效果而要求在井道壁开凿通风孔，往往受到很大限制。为了加工方便，高速电梯轿厢通风孔的形状多设计为矩形或椭圆环形，目前针对通风孔在轿厢侧壁周围的布局一般有3种方式：水平布局、垂直布局与环形布局，3种布局方式均采用等间距布局方式，其结构示意图如图1所示。

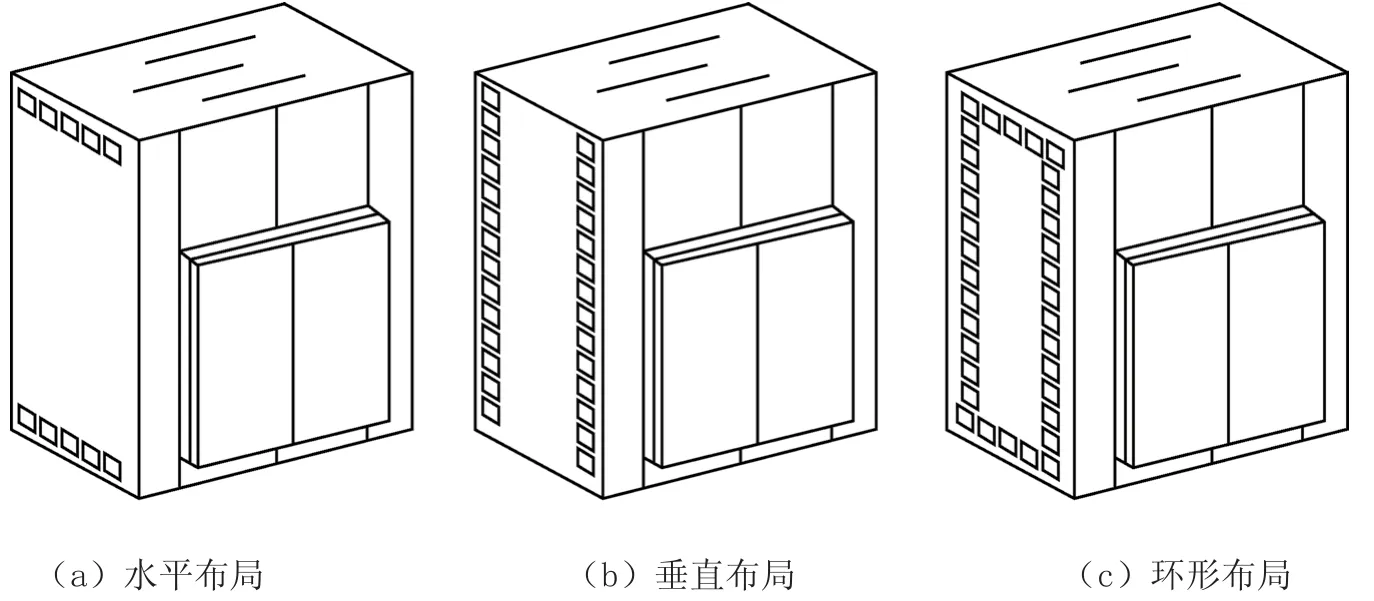
图 1 排气孔布局方式

其中，水平布局的通风孔对轿厢内顶部与底部气压变化的影响较大，适用于轿厢外气压变化不大、运行速度不高于4 m/s的高速电梯；垂直布局的通风孔对轿厢内前侧与后侧气压变化的影响较大，适用于轿厢外气压变化适中、运行速度不高于6 m/s的高速电梯；而环形布局则对轿厢内气压变化起到均匀影响的作用，适用于轿厢外气体产生激烈紊流、运行速度高于6 m/s的超高速电梯。

2 轿厢气压理论分析

2.1 轿厢气压流体运动基本方程

本文研究的是高速电梯运行过程中的轿厢内气压变化，轿厢内的气体属于流体力学中的粘性牛顿流体，故需要引入流体运动基本方程。流体运动基本定律可以用纳维-斯托克斯（Navier-Stokes）即N-S方程来描述，N-S方程主要由连续方程、动量方程和能量方程3部分组成，具体表达式分别为

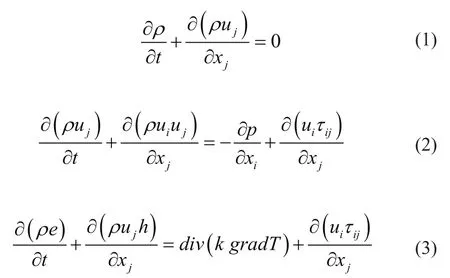
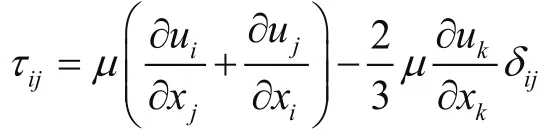
假设气体不可压缩，气流温度不变，则式（1）～（3）可简化为2个方程，其表达式为

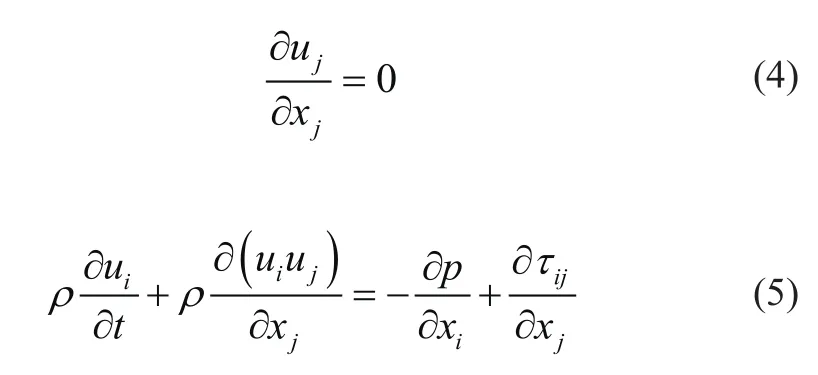
高速电梯运行过程中轿厢内气体流动非常复杂，会产生湍流现象，故需采用湍流模型进行仿真。

对于湍流问题的模拟，目前主要有3种方法：直接数值模拟、雷诺时均方程模拟和大涡模拟。直接数值模拟直接计算数值，适用于简单几何边界问题的模拟。雷诺时均方程引入了雷诺应力方向偏导数，同时将雷诺应力与湍流粘性系数μi建立联系，但在平均运动雷诺应力是未知的，需要建立湍流模型，会引入其他的未知数。大涡模拟结合了直接数值模拟和雷诺时均方程模拟的特点，通过滤波器将涡运动分为可以直接建立模拟求解的大涡运动以及建立压格子应力模型综合求解的小涡运动。对高速电梯轿厢气压湍流模型，采用盒式滤波器大涡模拟的方法最佳，其方程为

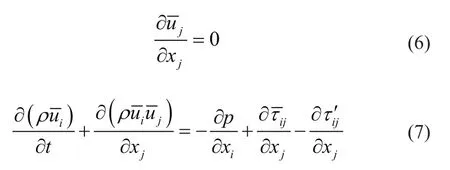
式中：ijτ′为亚格子应力，通过亚格子应力模型得到，最常用的亚格子应力模型为涡粘模型，其表达式为

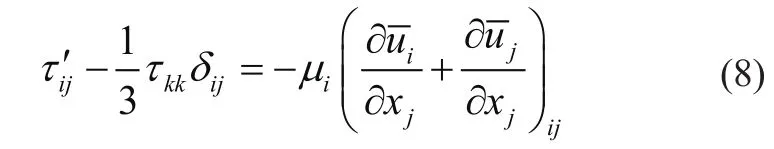
式中：μi为压格子湍流粘性系数，需要通过亚格子模型（如Smagorinsky-Lilly模型）求得。

2.2 高速电梯轿厢气压变化方程

理想气体状态方程

pV＝nRT

式中：p为气体压力，V为气体体积，n为气体物质的量，R为气体常数，T为气体热力学温度。

结合式(6)、式(7)，得出高速电梯轿厢气压变化的k-ε方程为

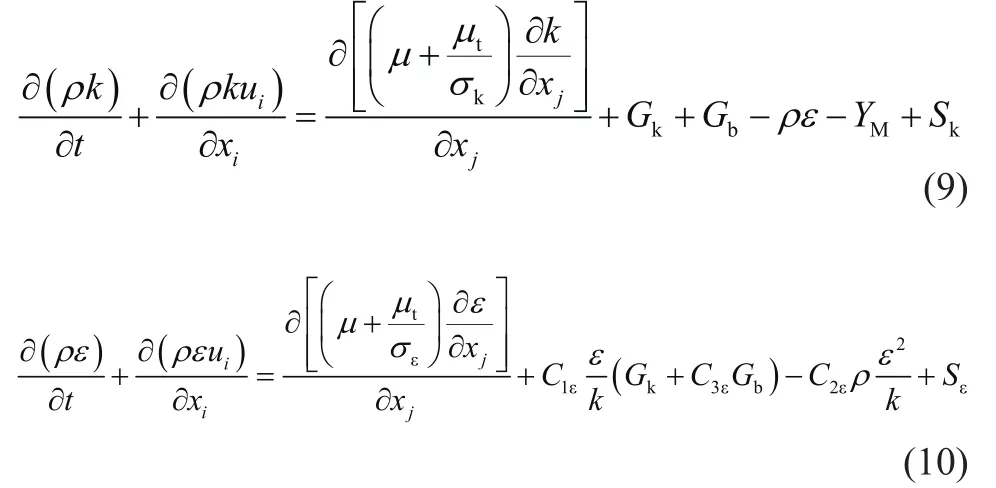
式中：ρ为轿厢内空气密度；xj为气体沿x、y、z方向的流速；μ为轿厢内空气动力粘度；μt为轿厢内空气粘性系数；Gk为气体速度梯度的平均数对应的湍动能；Gb为空气浮力对湍动能影响的变化值，对于轿厢气压变化其变化忽略不计；YM为可压缩流体的影响值，对于轿厢内气体为不可压缩其值为 0；C1ε、C2ε、C3ε、σk、σε、Sk、Sε为常数，其值分别取1.5、1.9，0，1.0，1.3，0；k为湍动能；ε为湍动能耗散率，其计算式为

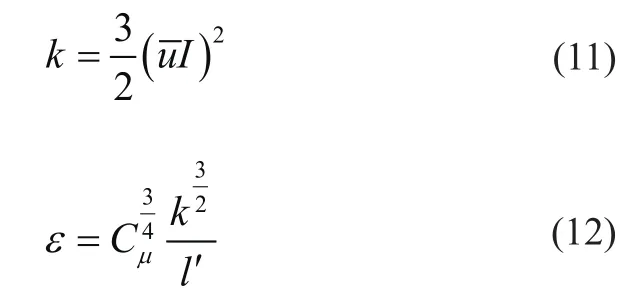
式中：为湍流平均速度；I为湍流强度，可取0.3%～0.8%；为常数，取0.1；l′为湍流的长度，根据实际情况而定。

3 建立高速梯物理模型

3.1 建立模型

图2为轿厢、井道物理模型及其简化图。电梯井道在结构上是细长型的，井道的长度（即深度）远大于井道的横截面积尺寸，轿厢的尺寸近似为长方体结构。为了便于表达图形和计算结果，本文部分示意图将只显示影响分析结果的图形局部位置。

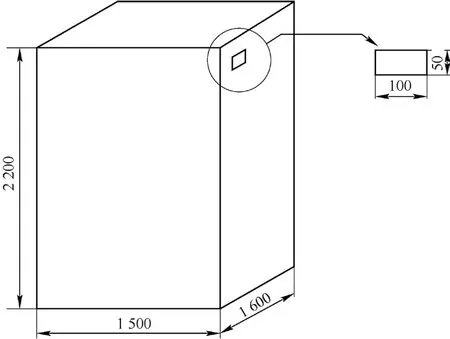
图 2 轿厢简易模型

简化的轿厢规格为1 500 mm×1 600 mm×2 200 mm，轿厢壁厚为2 mm的不锈钢，通风口的尺寸相比于轿厢应越小越好，这里选用100×50 mm的通风口。如图3所示，本次仿真共开12个通风口，通风口环形分布在轿厢的侧面。

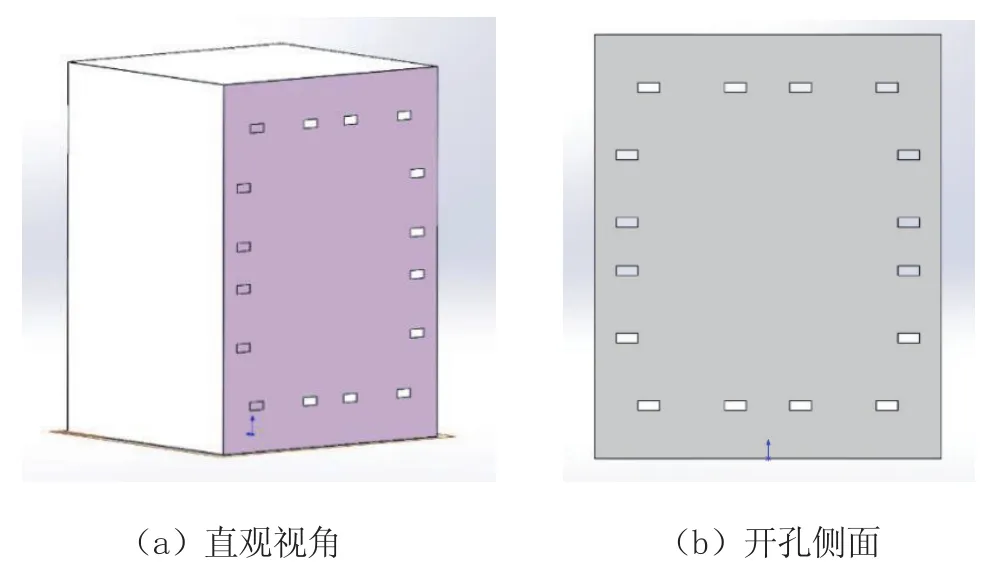
图 3 通气孔的分布

根据某高速电梯轿厢和井道之间的距离布置，轿厢门一侧距离井道200 mm，其余3个面皆为500 mm，如图4所示，井道深度按照接近实际的基础上减少网格数量的原则进行设定。于轿厢门的2个面设置若干通风口，且通风口的尺寸相同。

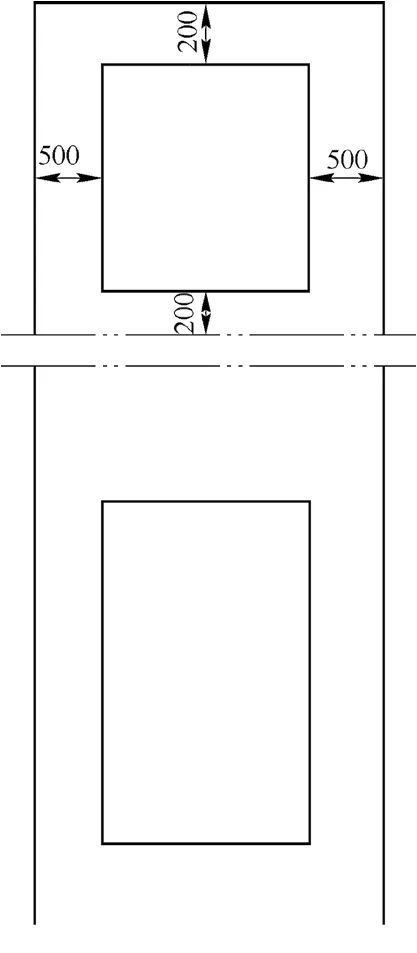
图 4 简化的电梯-井道尺寸

本文主要研究电梯在运行时，轿厢内的气压变化。为了方便仿真，需要做以下假设：

1）假设轿厢是一个规则的长方体，它在电梯井道做匀速运动。电梯轿厢的速度为6 m/s，一般情况下，当速度超过6 m/s以上时，轿厢的顶部、底部一般会增加整流罩，因导流罩的外形会对气流运动造成不同的影响，故此次仿真不设置导流罩。

2）假设该电梯为单部电梯，即没有与本电梯并排设置的电梯，或除了通风口外，此电梯井道与相邻电梯井道之间完全隔离。

3）本次实验中忽略井道上的通风口，轿厢上相邻

3.2 动网格设置

在Fluent中，当运动条件定义在边界条件上时提供了3种动网格运动的方法来更新变形区域内的体网格。即基于弹性变形的网格调整、动态的网格分层、局部网格重构。由于井道气动特性，仿真项目中需要采用动网格方法来模拟，一般井道长度大于轿厢运动距离，对网格质量提出更高要求。如果忽略边界效应会导致出现网格负体积的错误而终止模拟，且对于长距离的井道整个行程的动网格迭代次数过多、计算代价过大。在本文中为了避免出错，定义的网格类型为非结构性三角形网格，这类非结构性网格只能使用弹性变形的网格调整和局部网格重构的动网格生成技术，网格更细化，仿真更稳定，但相应的周期会略微增长。

3.3 网格划分

按照高速电梯在电梯井道中运行的简化模型和假设，用流体动力学分析软件Fluent的前处理工具建立井道模型，并用Gambit进行网格划分。考虑到电梯井道和轿厢模型各流动参数沿周向分布有流动不均匀现象，为了避免出现负体积错误，计算区域取为从气流入口到气流出口的整个流场，不采用单通道流域的方式。对于复杂的流道，计算中网格采用电梯轿厢非结构化网格，将模型进行网格划分，如图5所示。

图 5 简化的电梯网格

按照动网格的原理，网格会不断重构以适应轿厢移动，因此不用网格加密处理。用前处理工具 Gambit 划分网格，由于动网格技术的需要，采用电梯轿厢非结构化网格。完成网格划分后，总节点数为3 519，总网格数6 815，节点间距为0.2 m，经测试，网格质量、数量的满足计算要求。

3.4 设置边界条件

在Gambit中可以先预设置流体入口面、出口面、流体壁面以及轿厢实体壁面等边界条件，然后在Fluent中导入网格文件后设置替他边界条件和参数：

1）参考的环境压力：101 kPa即一个标准大气压；

2）流体入口边界条件：压力入口压力大小与环境压力一致；

3）流体出口边界条件：压力出口压力大小与环境压力一致；

4）轿厢顶和底的边界类型：移动刚体；

5）轿厢侧壁边界类型：变形刚体；

6）设置流体属性：理想气体；

7）其他设置：均采用默认仿真数据类型。

3.5 编译UDF程序

本次仿真中，需要定义电梯轿厢在电梯井道中的运行速度和方向。这些在Fluent接给出设置的界面。因此编写、编译并导入UDF程序只能根据Fluent用户自定义函数（UDF）接口。在本例中额定速度设置为6.0 m/s，电梯在距离井道顶500 mm的位置电梯向下运行并忽略加速、减速过程，按以上逻辑和参数编写UDF程序，在Fluent中进行编译并导入到数据文件中。

4 仿真分析及实验验证

4.1 初始化设置

初始化主要有检查网格、环境设置、动网格参数和动网格区域设置、定义轿厢运行的UDF程序的编译和导入、求解方程设置等过程。在求解时，设置时间步长为0.015 s，运行2 000步，迭代次数为20，仿真总共进行30 s，20个时间步长保存一次计算结果文件和Fluent数据文件，便于以后分析。

4.2 仿真结果和分析

本文中采用Cfdpost可视化工具进行后处理，并获得相关图例。本次仿真将井道按照离轿厢门由近到远，分为3个部分，分别为轿厢在井道前部（运行500时间步）、井道中部（运行1 000时间步）、井道尾部（运行1 500时间步）。并按照图6所示将轿厢按轿厢0.25宽度、0.5宽度、0.75宽度提取3个参考面。

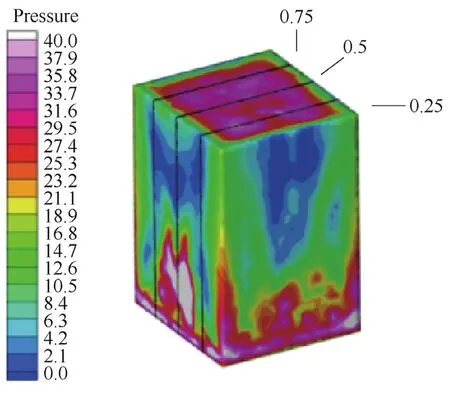
图 6 轿厢的三个参考面

仿真按照井道的3个部分对轿厢内的3个参考面单独做气压分析并列表，如图7所示。（图7中的气压值均以一个标准大气压值为标准，正值为高于一个标准大气压，负值为低于一个标准大气压）。

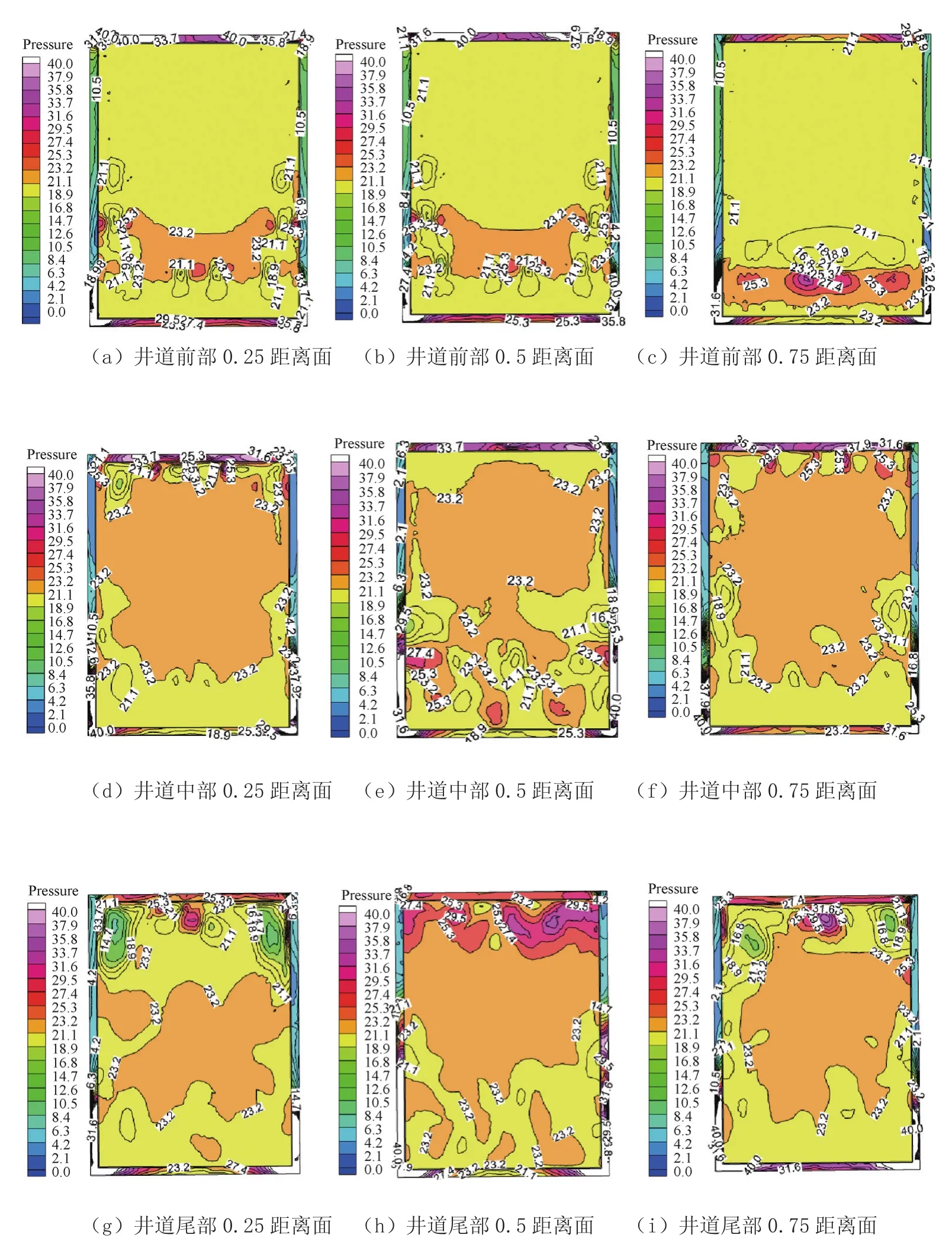
图 7 轿厢内气压云图

根据图7的仿真作业结果显示，在通气孔为环形布局，轿厢以6 m/s速度匀速向下移动的条件下，对轿厢内气体分布和压力进行分析（由于边缘效应，轿厢边缘处的数据对仿真结果的影响较大，不予考虑），可以看到在轿厢运动开始直至500时间步时，由于运动开始时速度从0突变至6 m/s。轿厢内的气体逐渐适应轿厢的速度，轿厢下部气压略微高于平均水平，但轿厢内气体分布基本均匀。当轿厢移动至1 000时间步时，高度的变化使得轿厢内气压总体呈上升趋势，小部分区域气压更大，当轿厢运动至1 500时间步后，轿厢内的气压继续增大，轿厢的上部开始出现高气压区域，其气压值明显高于轿厢的中部和下部。在轿厢的3个距离的参考面中，0.5距离参考面的气压变化更明显，仿真结果更具有代表性。

现选取3个参考面中相对于轿厢内上部的某一固定区域，对该区域从轿厢开始移动到轿厢运动结束时的气压生成连续变化曲线，如图8所示。

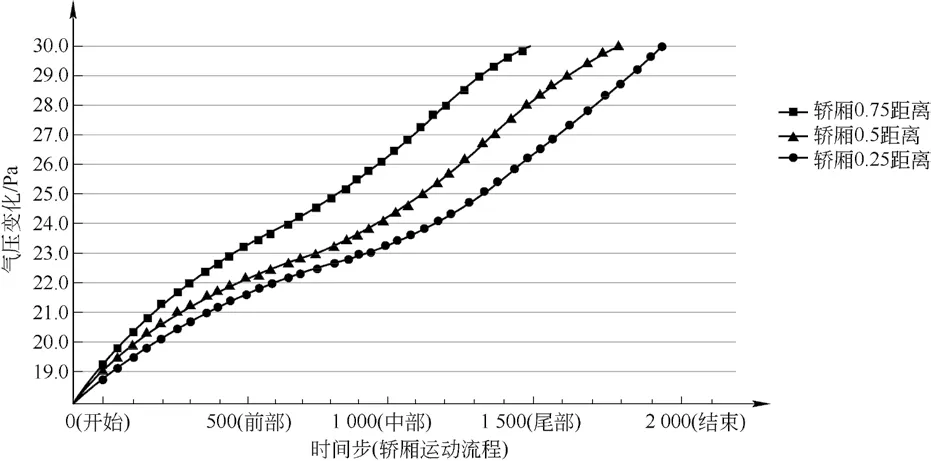
图 8 轿厢的3个参考面

电梯在匀速下行的过程中，轿厢内的气压值由小逐渐增大，且轿厢内越远离轿厢门的位置气压越大。在轿厢内偏上的位置变化更大，正好是乘客正常站立时头部所处的位置。结合理论分析，这正是乘客在轿厢中时常产生耳鸣现象的原因，由于气压变大较大的位置处于轿厢的上部，故身高较矮的儿童的耳鸣现象相对于成年人来说更加轻微。

4.3 实际测试分析

现对某高速电梯轿厢内实测气压进行实时测试，速度设定为4 m/s，上行和下行过程均测试一次。实验用到标智GM510数字压力表手持差压计与衡欣az88163号温湿度气压检测仪。

将实验测得的气压变化率描绘成曲线如图9所示，图中包括实验测量曲线、仿真模拟曲线以及残差曲线（由两者的实际值与拟合值之间的差），可以发现气压变化率逐渐增大的趋势，且由于实际测量时轿厢运行开始和结束处存在加速减速情况，变化率较大，中间过程趋于平稳，基本符合上述规律。

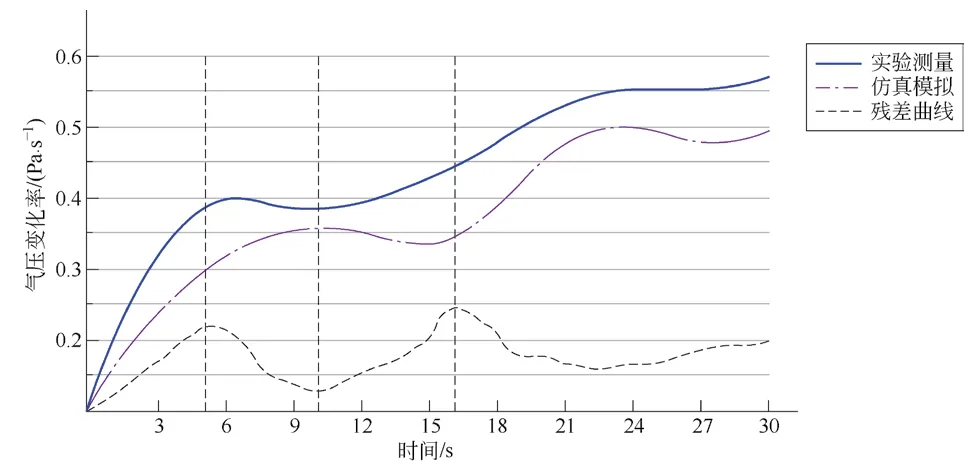
图 9 电梯变化率曲线

5 结语

本文以计算流体仿真方法对高速电梯运行时轿厢内部的气压进行了分析，并对仿真中电梯井道和轿厢内的流体运动边界设置及网格划分进行了更加符合实际操作场景的假设。

1）仿真结果显示，高速电梯运行时，轿厢内气压值处于均匀分布，其变化趋势呈线性，轿厢下行时气压增大，上行时气压减小。通过实际气压检测的实验,证实了文本方法的正确性。

2）在对轿厢内部结构进行划分后，可以明显看到轿厢内越远离靠近轿厢门的位置气压变化越快，轿厢中间且靠上部分区域的气压值达到当时整个轿厢内部气压的最大值，较大的气压变化会使乘客产生耳鸣现象，成年人更为严重，长时间乘坐无气压调节装置的电梯会引发各种疾病，出现安全隐患，如果合理的调节气压的平衡，能有效改善这一现象。