高铁隧道电气作业双臂系统稳定性数字化研究

郑雪楷 刘 放 杨 言 魏文清

西南交通大学机械工程学院 成都 610031

0 引言

随着社会的快速发展，大型工程项目不断实施，工程机械设备的需求也在日益增长。机械臂作业工程车是目前一类频繁使用的工程车辆[1]。

由于外载荷过重、环境复杂导致支腿伸缩受限和操作不够规范往往会引起车体失稳造成倾覆事故[2]。保证作业系统具有足够的稳定性，是机械臂作业工程车设计中最基本的要求之一。目前对起重机、高空作业车等机械臂作业工程车的抗倾覆稳定性的研究是针对最危险位姿。徐照新等[3]针对地铁高空作业车几个极限位置进行抗倾覆稳定性校核。张荣庚[4]也针对轨道式擦窗机几个极限位置进行抗倾覆稳定性校核。

对于机械臂作业工程车，由于工况的不同，车体支腿的伸缩量在某些时候无法达到最大，此时存在使车体发生倾覆危险的区域，而一些非工作需要的危险区域可以通过轨迹的规划进行避免[5]，这样可以在设计和生产制造上节约成本。通过建立数字化的抗倾覆稳定性计算公式，可以对机械臂式作业系统进行实时位姿的校核，快速有效的判断下一位姿是否会发生倾覆危险，由此可以有效地避免这些倾覆危险区域。

本文以高铁隧道电气作业双臂系统为研究对象，基于力矩法，建立抗倾覆稳定性的参数力矩方程。选取3种工况轨迹，运用Matlab计算各时刻的力矩大小，得到动态稳定力矩变化曲线。然后根据多体动力学理论，运用Simpack对高铁隧道电气作业双臂系统进行动力学分析，得到动态质心位移变化曲线。通过对比稳定力矩变化曲线和质心位移变化曲线，验证高铁隧道电气作业双臂系统抗倾覆稳定性数字化计算方法的正确性。

1 数字化坐标系的确定

1.1 高铁隧道电气作业双臂系统

高铁隧道电气作业双臂系统是一种由双机械臂组成的进行隧道接触网安装的作业系统，该系统包含工作臂机械臂和人工平台机械臂。工作臂机械臂采用了自动化控制，适用于装夹、安装等各种工况要求；人工平台机械臂用于装载工人配合工作臂机械臂进行施工。

由于高铁隧道电气作业双臂系统的流动性较大，对其校核抗倾覆稳定性时，根据结构特征，工作条件和对抗倾覆稳定性的要求进行校核，图1所示为双臂工作范围。

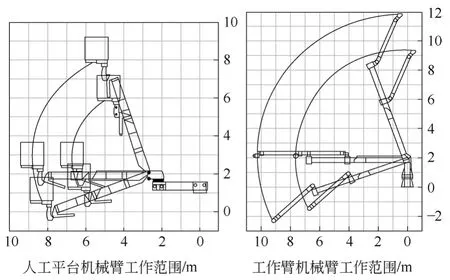
图1 双臂工作范围示意图

1.2 数字化坐标系的建立

机械臂操作的定义是指通过某种机构使零件和工具在空间运动。这就需要表达零件、工具以及机构本身的位置和姿态。为了定义和运用表达位置和姿态的数学量，必须定义坐标系并给出表示规则。通过坐标系描述位置和姿态用以表达所需的力和力矩。

如图2所示，以高铁隧道电气作业双臂系统的倾覆线上的一个支腿建立世界坐标系{W}，其次分别以车体重心、人工平台机械臂和工作臂机械臂的底座转动中心建立相对坐标系{C}、{R}和{G}。

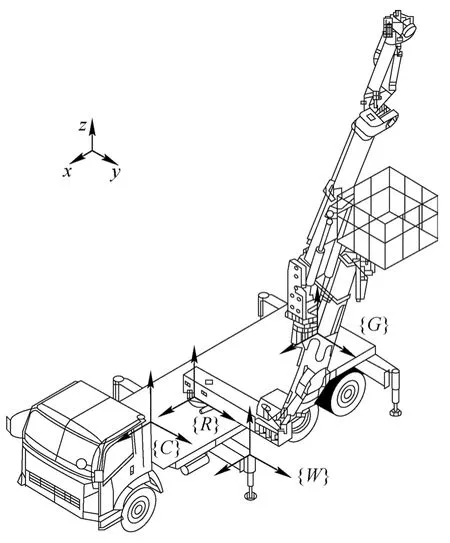
图2 双臂系统的数字化坐标系

2 抗倾覆稳定性分析

2.1 抗倾覆稳定性校核的基本原则

高铁隧道电气作业双臂系统抗倾覆稳定性是指高铁隧道电气作业双臂系统在自重和外载荷作用下抵抗倾覆侧翻的能力，此双臂系统属于起重机系列，故按照起重机的校核原则进行校核计算[6]。

当前，国内外对起重机抗倾覆稳定性的分析校核主要有力矩法、稳定系数法和按临界倾覆载荷标定额定起重量3种方法。由于我国GB/T 3811—2008《起重机设计规范》中所运用的是力矩法[7，8]，故采用此方法对高铁隧道电气作业双臂系统抗倾覆稳定性进行校核。在最不利的载荷组合条件下，计算各项载荷对双臂系统支承平面上的倾覆线的力矩，凡对双臂系统起稳定作用的力矩为正，起倾覆作用的力矩为负。各项力矩的代数和大于或等于零，则认为高铁隧道电气作业双臂系统是稳定的。抗倾覆稳定性校核的力矩表达通式为

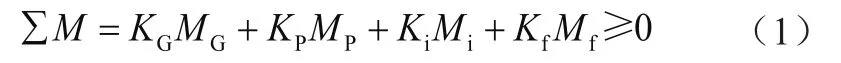
式中：MG、MP、Mi和Mf分别为起重机自重、起身载荷、水平惯性力和风力对倾覆线的力矩，KG、KP、Ki和Kf分别为上述4类载荷的载荷系数。

高铁隧道电气作业双臂系统的工作地点为隧道，整个过程都进行低速或定置工作，故工况选为无风静载。载荷系数分别为：KG=1，KP=1.25+0.1（Gb/PQ），Ki=0，Kf=0。其中，Gb为臂架自重对臂端和臂架铰点按静力等效原则折算到臂端的质量，PQ为起升载荷。

经过简化，臂架自重换算简图如图3所示，Gb＇按照式（2）进行计算

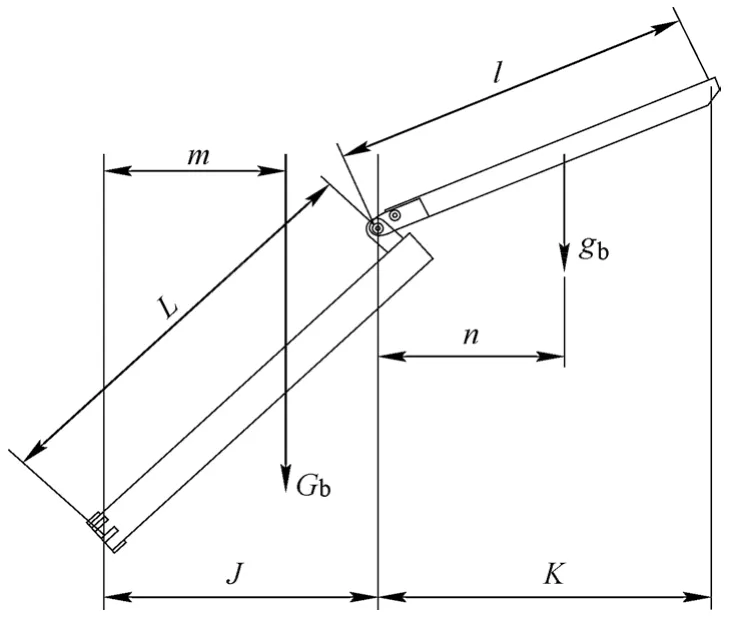
图3 臂架自重换算简图

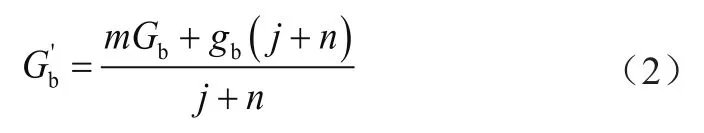
式中：Gb为主臂自重，gb为副臂自重，m为主臂重心到主臂下铰点的水平距离，n为副臂重心到副臂下铰点的水平距离，j为主臂长度L的水平投影，k为副臂长度l的水平投影。

2.2 危险倾覆边的确定

危险倾覆边是指车体绕其翻转并发生倾翻的轴线。危险倾覆边与高铁隧道电气作业双臂系统的构造、布局、臂架位置及验算工况有关。高铁隧道电气作业双臂系统使用支腿作业时，倾覆线为支腿中心的连线如图4所示。

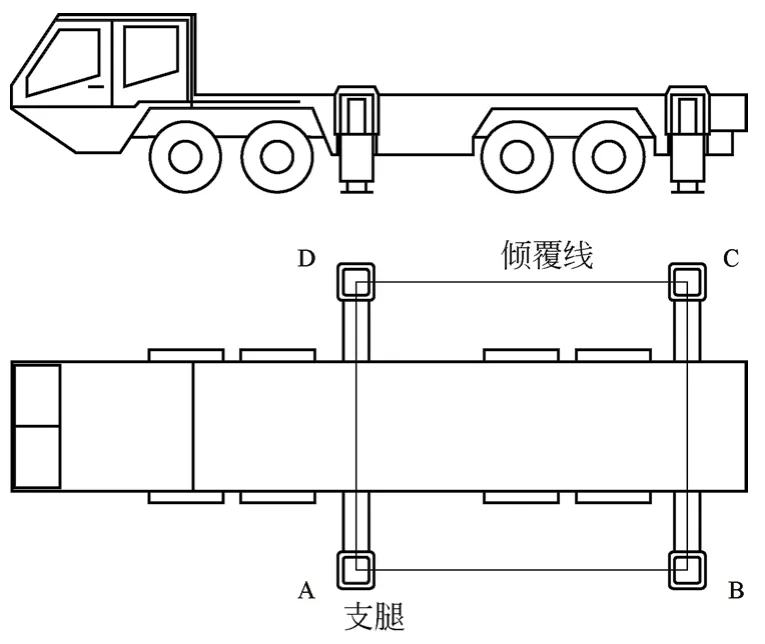
图4 汽车式起重机倾覆线示意图

2.3 抗倾覆稳定性数字化计算

通过上述所选机种类别及计算工况。基于力矩法，对高铁隧道电气作业双臂系统进行抗倾覆稳定性计算[9]。高铁隧道电气作业双臂系统的自由度及外载荷说明为：人工平台臂机械臂能够进行3个回转、2个伸缩及1个变幅的运动，人工平台始终受到1.5 t垂直向下的外载荷；工作臂机械臂能够进行2个回转、1个伸缩及2个变幅的运动，工作臂机械臂的头部始终受到0.7 t垂直向下的外载荷。同时由于受到地形和工况的影响，4个支腿的伸缩量也在实时的发生变化，并不一定保证在任何工作状况下伸缩量可以达到最长状态。

通过上述工况的选取，将载荷系数带入式（1）经化解得

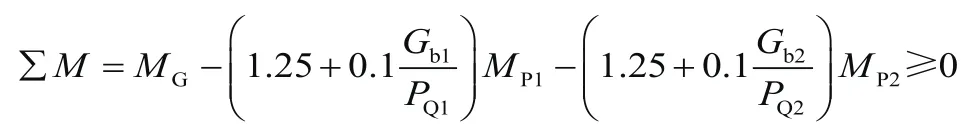
对高铁隧道电气作业双臂系统的一般状态进行参数化表示，根据图4可判断，当双臂位姿同时处于两侧即AB或CD边为倾覆危险工况。由于AB和CD的情况相似，现选取AB倾覆线进行校核。由于公式复杂，限于篇幅不再赘述，以含参项进行说明。

经过参数化后，起重机自重对倾覆线的力矩为：MG(θ1，θ2，θ3，β1，β2，β3，β4，β5，a1，a2，b1，lr1，lr2)；人工平台机械臂的臂架自重换算为：Gb1(θ1，a1，a2)；工作臂机械臂的臂架自重换算为：Gb2(θ2，a2，b1)；人工平台机械臂的外载荷对倾覆线的力矩为：Mp1(θ1，β1，β2，β3，a1，a2，lr1，lr2)；工作臂机械臂的外载荷对倾覆线的力矩为：Mp2(θ2，θ3，β4，β5，b1，lr1，lr2)；其中各参数含义及工作范围见表1

表1 双臂系统变量参数表

高铁隧道电气作业双臂系统在整个工作过程中存在着无数条运动轨迹。由于篇幅受限，本文选取3种工况进行动态求解。

根据数字化求解可知：1)通过动态曲线能够找到倾覆力矩最大的位姿，且符合最危险的位姿；2)得到抗倾覆稳定力矩的变化曲线，并与动力学仿真结果进行对比，验证得理论计算公式与预期相符；3)可清晰观测到使高铁隧道电气作业双臂系统发生倾覆侧翻的危险区域。

3种工况都选取支腿液压缸伸缩量等于0，同时双臂都处于危险倾覆边的同侧，经过Matlab的运算得到此3种工况运行轨迹下的稳定力矩变化曲线。

工况1：双臂由收缩状态到水平全伸状态，稳定力矩分析如图5所示。

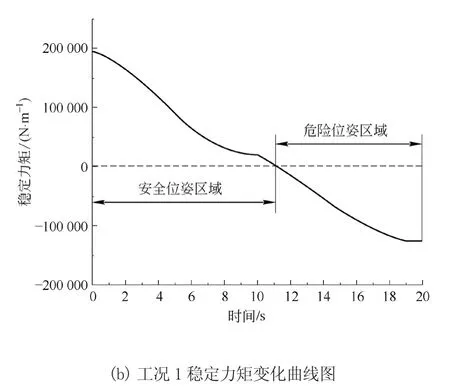
图5 工况1稳定力矩分析

工况2：双臂由水平全伸到俯角为20°全伸，稳定力矩分析如图6所示。

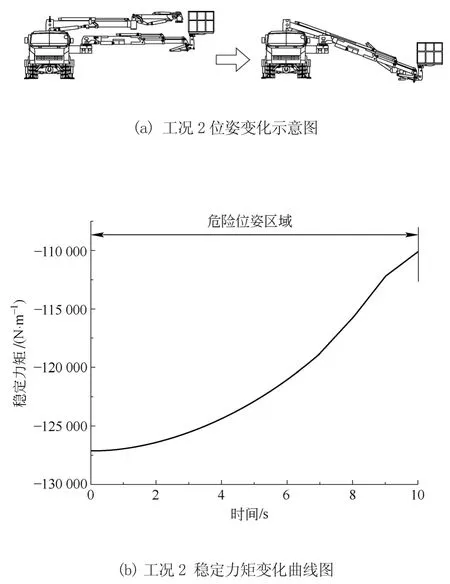
图6 工况2稳定力矩分析

工况3：双臂由水平全伸到仰角为70°全伸，稳定力矩分析如图7所示。

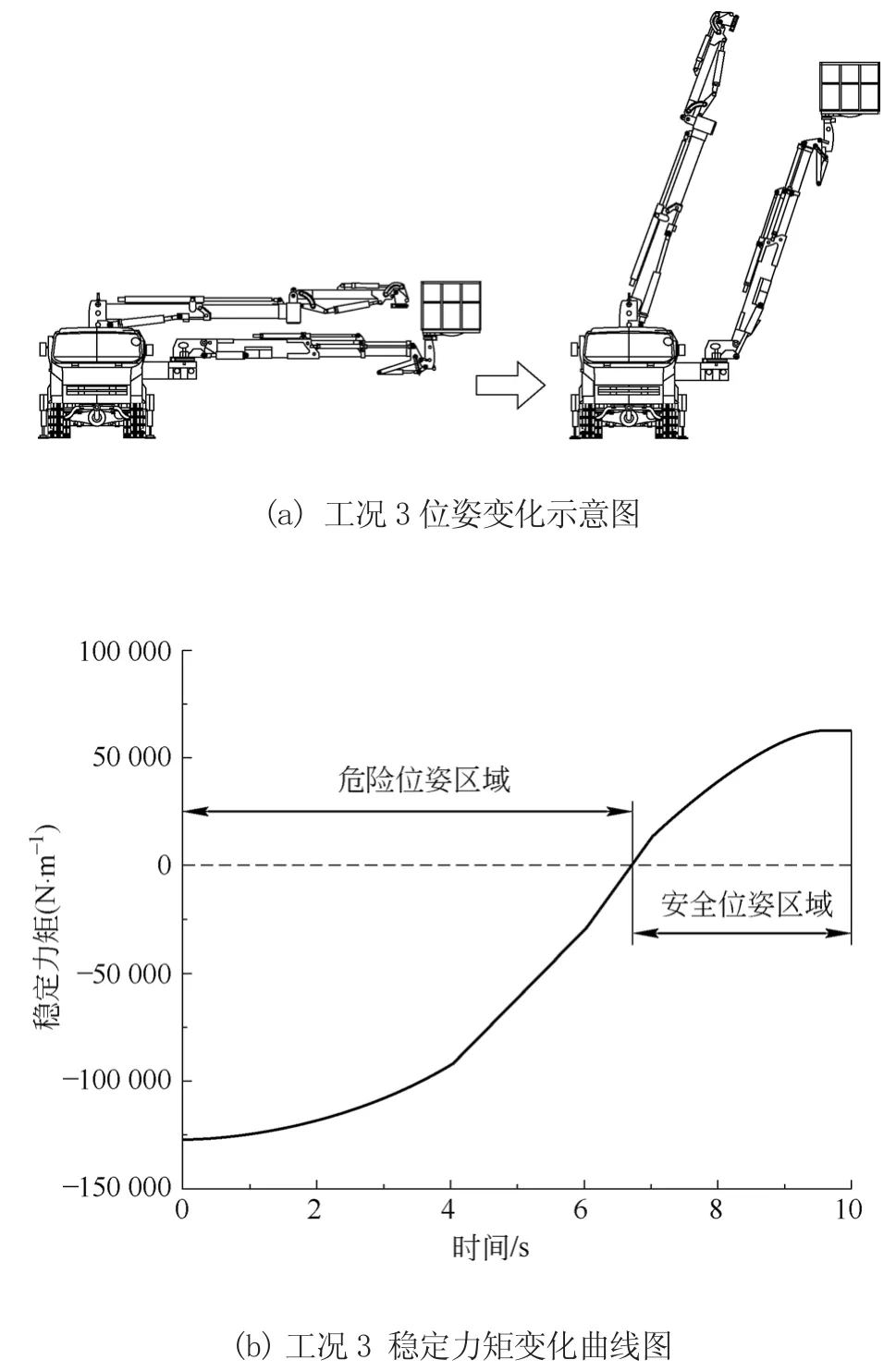
图7 工况3稳定力矩分析

在工作过程中，高铁隧道电气作业双臂系统易发生倾覆侧翻的位姿为双臂处于同侧，且水平全伸，此时支腿液压缸的伸缩量等于0。在这3种工况下，当时间达到工况1的11～20 s、工况2的全过程和工况3的0～6 s左右为倾覆危险区域。

根据抗倾覆稳定性数字化计算式可得，当支腿液压缸的伸缩量等于0时，高铁隧道电气作业双臂系统在工作过程中存在车体倾覆侧翻的危险区域。若遇到此类工况进行作业时要注意双臂的轨迹的控制，避免这些位姿的出现。

3 动力学分析

运用Simpack对高铁隧道电气作业双臂系统进行动力学分析仿真。根据多体动力学理论[10]，将高铁隧道电气作业双臂系统看成一个非线性多刚体系统，建立车体模型，由车体（1个）、臂架（22个）、液压缸（22个）共45个刚体组成。图8为高铁隧道电气作业双臂系统的动力学模型简化拓扑图。

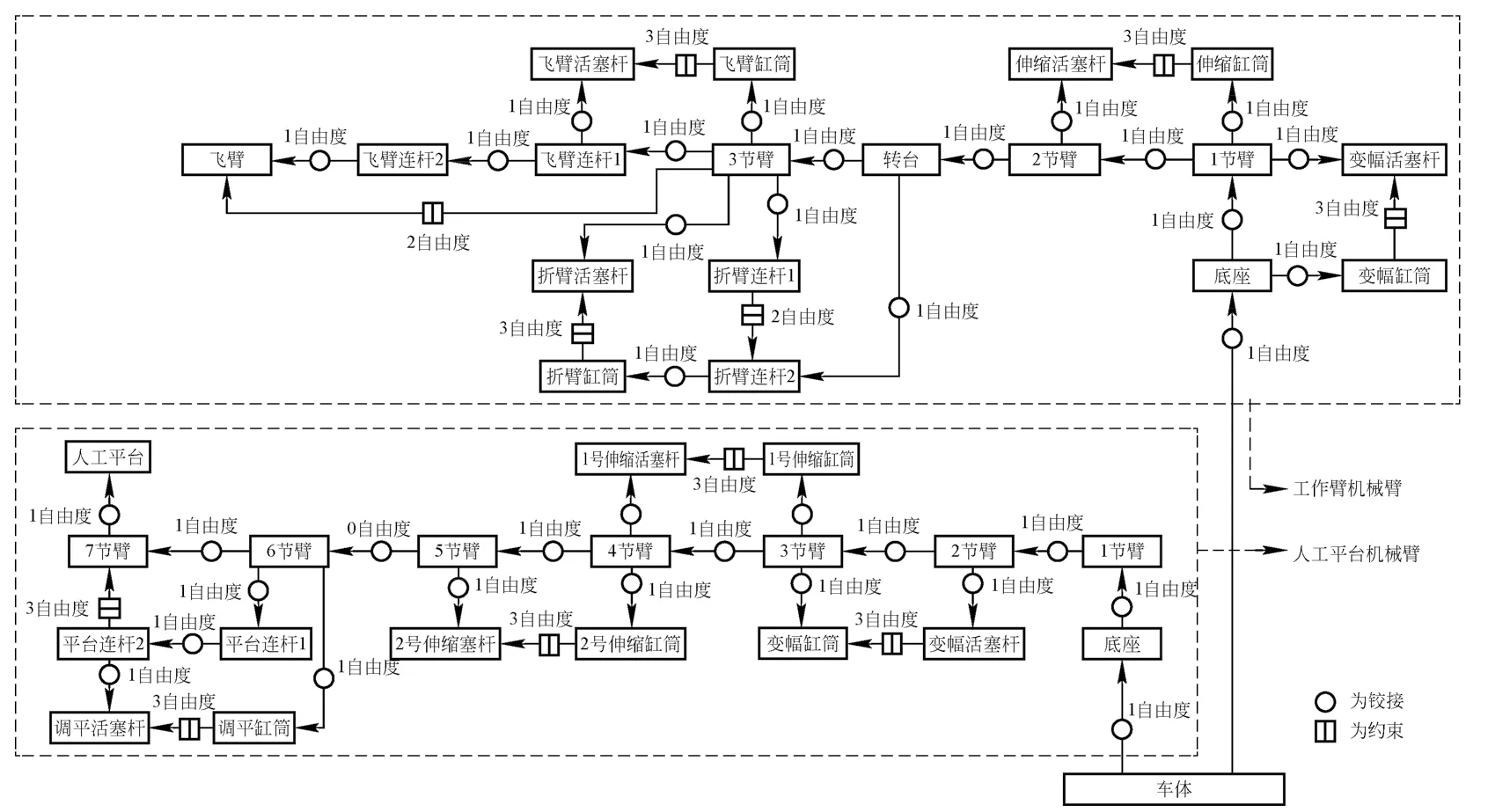
图8 动力学模型简化拓扑图

通过对高铁隧道电气作业双臂系统的动力学分析[11]，对高铁隧道电气作业双臂系统的质心位置进行动态求解，并给出了与第2节同样工况的质心到倾覆线的距离随时间的变化曲线。

工况1：双臂由收缩状态到水平全伸状态，工况1质心位移曲线如图9所示。

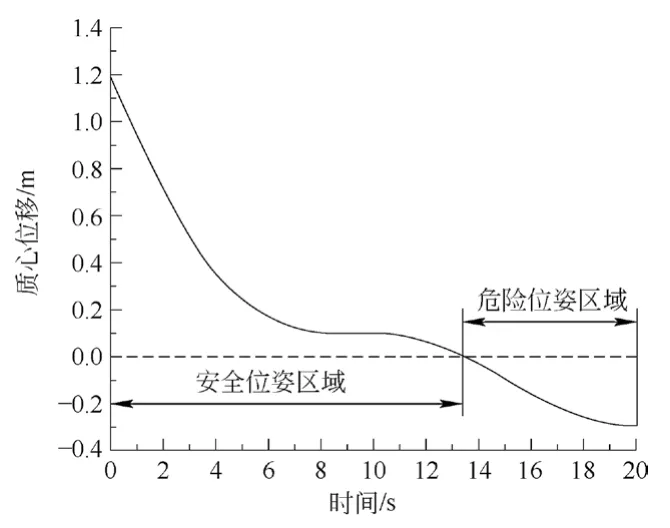
图9 工况1质心位移曲线图

工况2：双臂由水平全伸到俯角为20°全伸，工况2质心位移曲线如图10所示。

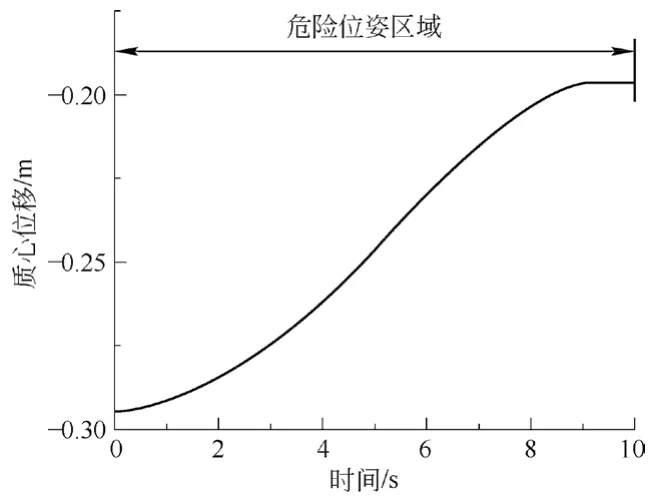
图10 工况2质心位移曲线图

工况3：双臂由水平全伸到仰角为70°全伸，工况3质心位移曲线如图11所示。

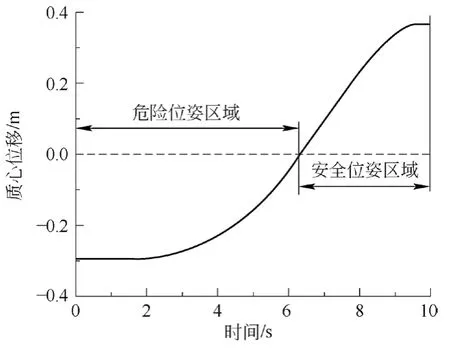
图11 工况3质心位移曲线图

根据仿真结果，高铁隧道电气作业双臂系统的质心位置随着双臂系统位姿的变化而发生变化，同样大概在时间达到工况1的11～20 s、工况2的全过程和工况3的0～6 s左右质心位置移动到倾覆线外，即为倾覆危险区域。此时高铁隧道电气作业双臂系统存在倾覆危险。通过与稳定力矩变化曲线的变化情况作对比，2条曲线随着时间的变化趋势一致，即仿真结果与理论计算结果一致，与预期结果相符。

4 结论

1)通过力矩法所求得的稳定力矩变化曲线和Simpack动力学仿真的质心位移曲线的对比，2条曲线的变化趋势和发生倾覆危险的临界位姿的相符。验证了所求解的抗倾覆稳定性校核力矩参数表达式的可靠性和正确性；

2)运用抗倾覆稳定性校核力矩参数表达式，求解各位姿的稳定力矩。通过轨迹规划避免这些非工作的倾覆危险位姿，不用每个位姿必须稳定安全，这样可以在设计制造方面节约成本和人力。