基于AOA-CRHJ的曳引电梯钢丝绳动态张力预测方法*

陈向俊 傅军平 李 科 陈栋栋 李黎苹

1浙江省特种设备科学研究院 杭州 310020 2浙江省特种设备检验技术研究重点实验室 杭州 310053

0 引言

钢丝绳是曳引式电梯的重要组成部分，对电梯的运行安全影响重大，钢丝绳的张力承载是有极限的，电梯运行时动态张力过大，是钢丝绳断裂的重要原因[1]。2020年宁波某电梯因钢丝绳断裂致使14人被困；2021年长沙某电梯钢丝绳断裂坠落使2人被困，对群众生命财产安全造成极大威胁。当钢丝绳在下行加速时，钢丝绳的张力逐渐增大，当张力过大导致钢丝绳断裂时，将会造成巨大的生命财产损失。而通过对钢丝绳的动态张力进行预测，可及时制止事故发生。

现有对张力过大预防的研究是通过对钢丝绳的直径进行检测，寻找钢丝绳薄弱部位，判断钢丝绳是否可以正常使用[2]，这在一定程度上保障了电梯安全，但钢丝绳在运行过程中，单根钢丝绳之间所受张力必然存在一定偏差，当钢丝绳安装磨损等导致张力不均时，可能会发生单根钢丝绳承受张力过大导致事故发生。本文提出一种新的电梯钢丝绳张力预警方法，通过连接在轿厢侧绳头的压力传感器对钢丝绳张力进行动态检测[3]，利用获得的数据建立基于机器学习的时间序列分析模型，预测电梯运行过程中的张力最大值，判断电梯钢丝绳是否安全可靠，以此避免事故发生。

钢丝绳的安全性十分重要，其动态张力数据属于典型的时间序列，故实现对钢丝绳张力的预测需要高稳定性和快速反应能力。时序预测中基础的回归拟合，如整合移动平均自回归模型(Autoregressive Integrated Moving Average model，ARIMA)[4]等，通过拟合出一条最符合历史数据的曲线，对未来数据进行延伸预测，该方法较为简单方便，但误差较大。传统回声状态网络(Echo State Network，ESN)等模型由于储备层具有随机性[5]，内部结构并不稳定，内部性能难以控制。ESN的改进算法——确定性循环跳跃网络(Cycle Reservoir with Regular Jumps，以下简称CRJ)[6]采用确定的储备层结构，一定程度上提高了模型稳定性，但其内部的结构缺乏活力，性能不够突出[7,8]。因此，本文采用确定性分层跳跃网络(Cycle Reservoir with Hierarchical Jumps，CRHJ)[9]在CRJ的模型上改进为多层跳跃，提高了隐藏层的活跃性，保证了神经元稳定性和活跃性并存。同时为解决CRHJ模型性能过于受制于超参数影响，结合阿基米德优化算法(Archimedes Optimization Algorithm，AOA)[10]对CRHJ模型的隐藏层个数、训练次数、学习率等参数进行优化。本文使用电梯下行过程中采集的单根钢丝绳压力数据，利用多种算法对数据进行处理预测，以此对比验证本文所采用模型的有效性。

1 理论与算法

1.1 CRHJ网络模型

相较于其他传统时间序列预测模型，ESN有着训练速度快的优点，这使其能在张力预测这种短时预测上具备优势[11]。确定性分层跳跃网络(CRHJ)是其改进算法，区别在于将ESN的随机连接储备池改成了确定的循环拓扑结构，使其性能变得可控。在提高模型内部稳定性的同时保证内部单元的活跃度，使其可以快速准确地进行时序预测。

CRHJ结构如图1所示，与传统回声状态网络相同，CRHJ同样由输入层、输出层与储备池构成为

图1 CRHJ网络结构图

输入层的k个输入单元先与输入权重Win相乘后，进入储备池h(n)运算，再与输出权重Wout运算获得输出y(n)。CRHJ与ESN不同之处在于改进了模型的储备池h(n)，传统ESN储备池随机连接，模型具有不稳定性，在对张力进行时序预测时精确度难以保证。而CRHJ模型对此进行改进过，将储备池改成确定的分层跳跃拓扑结构。当储备池神经元个数为N时，储备层的各神经元先以单向连接权重相互连接，分层双向跳跃权重ri再双向连接N个内部单元，i为权重层数，跳跃步长为J(1＜J＜N/2)。单向连接权值、双向分层连接权值、储备池神经元、跳跃步长构成了CRHJ不同于ESN的环形拓扑结构。相较于确定性循环跳跃网络(CRJ)，模型有更深的连接层，在进行常规跳跃后，可在更高的跳跃层进行跳跃，这使得CRHJ有着更高的稳定性、可控性及预测性能，适合于本文的张力预测。

CRHJ的储备池更新公式为[12]

式中：f为储备池的激活函数，一般可取为tanh函数或sigmoidal函数；W为储备池的权值矩阵；z(n)为独立均匀分布的随机噪声。CRHJ的输出为

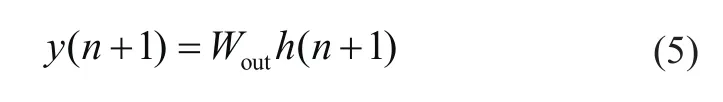
1.2 AOA优化算法

在确定CRHJ的预测方法后，模型的参数选取依然存在问题。CRHJ模型的性能主要由神经元个数、跳跃步长、跳跃层深度等影响，参数的选取对模型的可靠性影响很大。而基于经验，没有确定标准的参数选取在实际应用中会限制模型的泛用性和可靠性。故本文选用阿基米德优化算法(AOA)对模型的参数进行寻优。

作为一种元启发式算法，AOA算法的思想来源于阿基米德原理，基物体所受浮力与其排出流体质量成正比[13]。与其他基于群体的元启发式算法一样，AOA也从具有随机体积、密度和加速度的初始对象群体（候选解）开始搜索过程，在这个阶段，每个对象也被初始化为它在流体中的随机位置。在评估初始种群的适应度后，AOA在迭代中工作，直到满足终止条件。在每次迭代中，AOA都会更新每个对象的密度和体积。对象的加速度根据其与任何其他相邻对象的碰撞条件进行更新。更新后的密度、体积、加速度决定了物体的新位置。其具体步骤为：

1)初始化 初始化所有对象的位置为

初始化第i个对象的体积vol和密度den为

最后，初始化第i个对象的加速度acc为

式中：ub、lb为变量的上下边界。

评估初始总体并选择具有最佳适应度的对象xbest、denbest、accbest。

2)更新密度及体积为

3)计算转移算子与密度因子

起初，物体之间发生碰撞，经过一段时间后，物体试图达到平衡状态。这是在AOA中通过传输运算符TF实现的，该运算符将搜索从探索转换为利用，定义为

同样，密度递减因子d也有助于AOA进行全局到局部搜索。其随时间的推移而减少，定义为

4)探索阶段(对象之间发生碰撞)

若TF≤0.5，对象之间发生碰撞，选择1个随机材质mr使用式(12)更新迭t+1代时的对象的加速度为

5)开发阶段(对象之间无碰撞)

若TF＞0.5，使用式(13)更新迭t+1代时的对象的加速度为

6)归一化加速度使用式(14)计算变化百分比

7)对象位置更新

若TF≤0.5，第i个t+1迭代时对象位置更新为

若TF＞0.5，第i个t+1迭代时对象位置更新为

阿基里德算法通过传输运算符的更新在探索阶段与利用阶段更换[14，15]，保持全局寻优与局部寻优之间的平衡，能有效避免存在多局部最优解的复杂优化问题，可有效解决CRHJ前置参数较多且难以凭经验对不同数据进行寻优的问题。阿基里德算法具有优秀的检索能力和更广的检索范围，适合于对CRHJ模型的参数优化。

1.3 基于AOA-CRHJ的钢丝绳张力预测模型

本文将AOA算法与CRHJ算法结合，构成新的AOA-CRHJ预测模型。本文预测流程如图2所示，将采集的电梯下行实验中的钢丝绳张力值作为原始数据，通过归一化后划分为训练数据与验证数据，使用训练数据对由阿基米德算法进行超参数寻优后的CRHJ模型，即AOA-CRHJ进行训练并预测。通过与验证数据对比，计算预测结果的均方根误差（Root Mean Square Error，RMSE）与平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）对模型的预测精度进行评判。其具体实现如下：

图2 基于AOA-CRHJ的钢丝绳动态张力预测流程

1）输入电梯下行实验中的张力变化数据，经过归一化后，划分为训练数据与验证数据；

2）初始化CRHJ中的参数，包括储备池单元个数、跳跃步长、跳跃层深度、迭代次数等参数；

3）基于AOA算法的CRHJ参数寻优。首先初始化代表参数的对象位置、以训练集的均方根误差作为适应度函数，每一次迭代都更新对象密度、体积及转移算子，依据转移算子判断进行开发阶段或是探索阶段，分别对应局部寻优及全局寻优。通过对参数值进行探索开发，返回具有最优适应度的一组参数；

4）依据3)中返回的最优组参数对CRHJ模型重新初始化，再次训练得到训练后的AOA-CRHJ模型，并使用模型预测未来区间张力，并通过与验证数据对比判断模型性能。

2 实例分析

2.1 数据来源

本文数据通过压力传感器结合记录分析仪在电梯下行实验中采集。采用传感器最大量程为1 250 kg、平均采集误差为0.1%、测量通道为12通道、绳头组合为M10～M20、采集速度为60次/min、检测精度为0.1 kg。本文所采集的电梯参数为：载重量1 600 kg、钢丝绳总计6根、曳引比为2:1、钢丝绳直径13 mm、运行速度3 m/s。

记录前将压力传感器安装在轿厢的侧绳头上，通过上位机接受传感器数据，提升轿厢高度后控制电梯下行，并记录下行中的钢丝绳张力变化。本文共采集动态张力值38组，以前32组作为训练样本，后6组作为测试样本，如图3所示。

图3 实测电梯钢丝绳动态张力数据

2.2 评估指标

本文采用均方根误差RMSE及平均绝对百分比误差MAPE作为模型评判标准。RMSE、MAPE越接近于0时，模型的预测精度越高。RMSE与MAPE的计算公式为

2.3 AOA-CRHJ模型预测

以模型的均方根误差RMSE为阿基米德算法的适应度，通过不断迭代对CRHJ模型进行寻优，使用优化后的模型对钢丝绳张力进行预测。设定AOA的返回条件为迭代次数达到100，设定CRHJ迭代次数上下限为100～1 000整数，单向跳跃权重ro∈ (0,1]，双向跳跃权重ri∈ (0,1]，跳跃步长1＜J＜N/2，储备池规模设置为1～200整数。由预测结果图4可知，通过迭代寻优后，CRHJ对张力的预测可达到较好的效果，计算得均方根误差RMSE为3.6197，平均绝对百分比误差MAPE为0.19%。

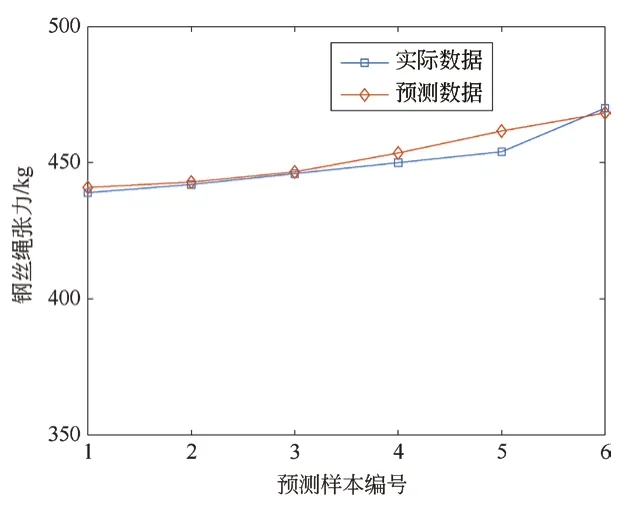
图4 AOA-CRHJ模型预测结果

2.4 对比实验

为进一步对比验证AOA-CRHJ模型在张力预测上的可靠性，分别使用LSTM及ESN对数据进行分析预测。LSTM和ESN都是应用广泛的时间预测模型，在诸多领域都有不错的效果。本文通过对LSTM及ESN模型选取其中的最优情况来进行对比。LSTM神经元个数设定为400，学习率设为0.004，并在100步后降为0.000 8，训练步数设定为1 200；ESN网络以训练集前10组数用于激活ESN储备层，储备池规模设为1 000，储备池更新速度为1。预测结果分别如图5、图6所示。

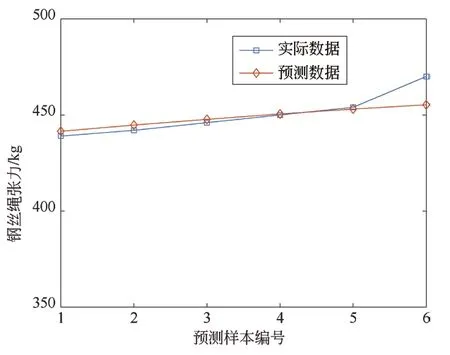
图5 LSTM模型预测结果

图6 ESN模型预测结果

计算可得各模型预测结果的均方根误差RMSE及平均绝对百分比误差MAPE如表1所示。

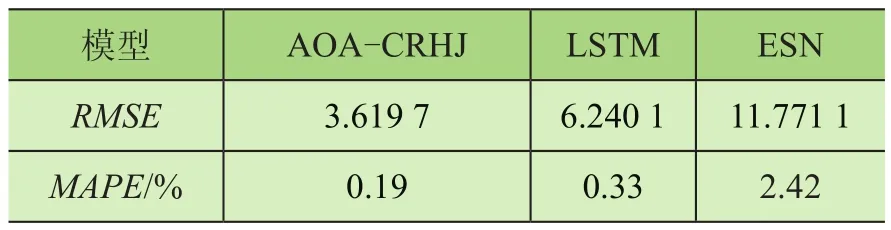
表1 对比预测结果评价指标

从表1中可知，AOA-CRHJ模型相对于传统LSTM及ESN模型都有较大的性能提升，相较于LSTM的均方根误差减少了42%，平均绝对百分比降低了43%，而ESN模型由于数据量相对较少，难以很好地激活储备层并获得优秀的预测效果。由此可以说明在钢丝绳张力的短时预测方面，AOA-CRHJ模型有着明显高于其他模型的预测精度和预测可靠性。

3 结语

针对曳引式电梯钢丝绳运行过程中张力动态变化影响电梯运行安全的问题，本文在确定性分层跳跃循环网络CRHJ的基础上，利用阿基米德算法AOA对模型参数进行优化，提出了AOA-CRHJ模型。AOA-CRHJ模型具有较高的预测精确度和可靠性，且泛化能力强，可以对不同受力状态的钢丝绳动态张力变化进行很好的预测。本文利用压力传感器所采集的电梯空载下行实验的钢丝绳张力变化数据，通过与LSTM模型与ESM模型进行对比，发现本文所提出的AOA-CRHJ模型相较于传统时间序列预测模型至少具有45%的性能提升，表明了本文提出的深度学习模型的在电梯钢丝绳动态张力预测方面具有潜在优势。