基于响应面法-满意度准则的混合骨料充填体强度发展与优化分析
2022-03-29胡亚飞李克庆韩斌李宏业赵金田北京科技大学土木与资源工程学院北京10008北京科技大学金属矿山高效开采与安全教育部重点实验室北京10008金川集团股份有限公司甘肃金昌77100
胡亚飞,李克庆,韩斌,李宏业,赵金田(1.北京科技大学土木与资源工程学院,北京,10008;2.北京科技大学金属矿山高效开采与安全教育部重点实验室,北京,10008;.金川集团股份有限公司,甘肃金昌,77100)
充填采矿法具有降低矿石损失、提高生产率、控制采场地压、充填空区避免塌陷、减少地表废石堆积等作用,被广泛应用于地下金属矿山开采中[1-3]。随着浅部资源枯竭,我国多数矿山正转入深部开采阶段,而充填法是保证深部安全开采最有效的手段之一[4-6],因此,有必要对充填材料及充填配比进行深入研究,以确保充填强度满足生产要求。
国内外学者对影响充填体强度的充填材料和配合比开展了大量研究。付自国等[7]开展了废石-风砂充填强度试验,发现当废石与风砂的质量比为7∶3时骨料具有最大堆积密实度,此时,充填体强度最大;高谦等[8]开展了基于RSM-BBD 的混合骨料充填配比优化,确定了废石-棒磨砂最佳骨料配比,并建立了充填体强度模型;侯永强等[9]基于RSM-BBD法研究了混合骨料胶结充填体强度增大规律,得到了充填体强度回归模型,并优化了充填配合比;尹升华等[10]采用响应面实验探究了多种骨料混合充填的优化配比研究,分析了各因素对充填强度的研究机制,并采用目标规划法实现了配合比寻优;杨啸等[11]为研究混合骨料充填体强度增大规律,构建了神经网络强度预测模型,实现了充填体强度的高精度预测;张超等[12]基于骨料堆积密实度理论研究了混合骨料配比对充填体强度的影响,发现存在最佳骨料配比使充填体强度最大,此时混合骨料最密实。上述研究对充填材料的选择及配合比设计具有一定的指导作用,但采用传统的级配理论无法对骨料的孔隙结构进行定量表征,使骨料配比设计存在一定的片面性;此外,传统上通过研究单因素开展充填配比优化的方法忽略了多因素综合作用的影响。
本文作者针对混合骨料充填时配比不易确定的问题,利用分形理论对混合骨料孔隙结构进行定量表征以寻求最佳骨料配比;采用响应面法研究骨料配比、料浆质量分数以及胶凝材料掺量等单因素和复合因素对充填体不同养护龄期强度的影响,并建立强度响应回归模型;基于满意度准则的多目标优化算法实现混合骨料充填配合比的优化。
1 分形理论优化混合骨料级配
1.1 充填骨料级配分析
实验用混合骨料为金川镍矿采用的废石破碎集料和河砂混合料,这2种骨料的化学成分多为惰性物质,较稳定。废石破碎集料作为粗骨料其最大粒径为12 mm,主要由矿山井下开拓和回采过程中拉运的废石经破碎机破碎而成;河砂为细骨料,其最大粒径为9.5 mm。这2种充填骨料的粒度参数见表1。

表1 充填骨料粒度参数Table 1 Particle size parameters of filling aggregate
骨料级配是影响充填体强度的重要因素,采用Talbol级配理论对废石破碎集料和河砂的级配进行评价,当级配指数为0.5左右时,骨料级配较为理想。骨料粒径小于或等于d的含量与总量的关系如下:
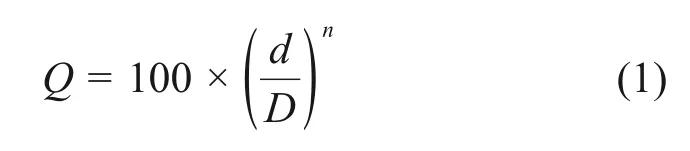
式中:Q为粒径d的骨料通过百分率,%;D为最大粒径,mm;n为Talbol级配指数。
按照式(1)分别对河砂和废石破碎集料的级配进行拟合,得到2 种骨料的级配曲线见图1。由图1 可知:河砂级配指数n为0.339,低于0.500,说明河砂细粒级占比偏大,需要添加粗骨料进行优化;废石破碎集料级配指数n为0.651,高于0.500,说明废石粗粒级占比偏大,需要添加细骨料改善级配。因此,考虑将2种骨料混合作为充填骨料。
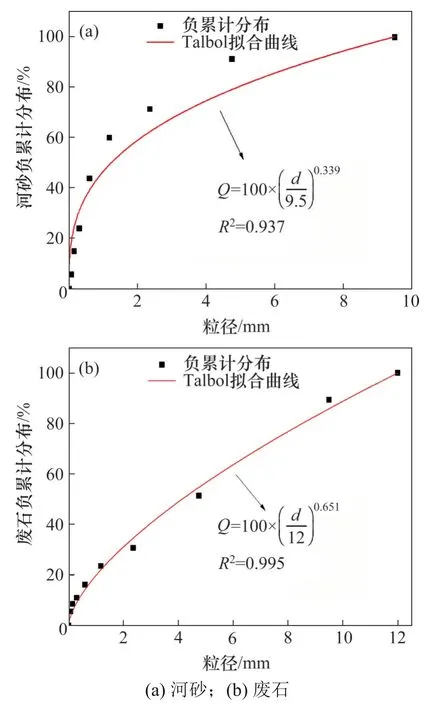
图1 充填骨料粒度特征曲线Fig.1 Particle size characteristic curve of filling aggregate
1.2 分形理论优化骨料配比
充填骨料是由粗、细砂石混合而成的多孔介质材料,具有较强的非均质性,骨料间接触产生大量不规则的孔隙,这种孔隙结构呈现明显的自相似性和分形特征[13]。采用传统级配理论无法精确描述混合骨料内部复杂的孔隙结构特征,因此,考虑采用分形理论对混合骨料的孔隙结构进行定量表征,以寻求最佳混合料配比。
破碎砂石属于自相似碎体,其颗粒数目与粒径呈幂指数关系[14]:

式中:N(r)为粒径小于r的骨料颗粒数;K为常数;E为分形维数。
骨料颗粒的质量与粒径之间服从韦布尔分布[15]:

式中:M(r)为粒径小于r的骨料质量;M0为骨料总质量;r0为骨料平均粒径;α为骨料质量与粒径的关系指数。
对式(2)和式(3)两端进行求导可得:
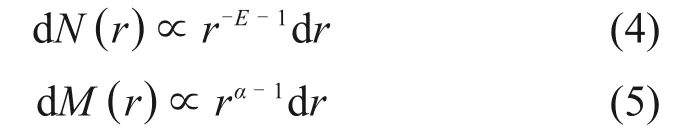
骨料颗粒数与质量增量的关系为dN∝r-3dM,结合式(4)和式(5)可得

骨料堆积结构孔隙的分形维数Ek可以反映骨料孔隙结构的分布特征,与E的关系为[16]
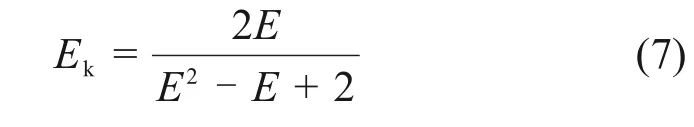
由此得到混合骨料堆积结构分形维数Ek模型为

基于分形理论计算不同废石、河砂配比混合料孔隙结构的分形维数Ek见图2。由图2 可知:随着废石集料在混合料中占比(即废石质量分数)增大,混合料孔隙结构分形维数呈先增大后减小的趋势;当废石质量分数小于60%时,分形维数随废石质量分数增加而增大,废石在混合料中充当骨架,河砂主要起填隙作用,废石与河砂之间逐渐由松散结构变为嵌锁结构,混合料结构密实度增加,孔隙结构空间占据能力增强,因此,其分形维数增大;当废石质量分数为60%时,废石与河砂之间完全构成嵌锁结构,此时分形维数最大,混合料最密实;当废石质量分数大于60%时,河砂量相对变少无法完全填充骨架结构,混合料结构松散,因而,分形维数随废石质量分数增大而减小。因此,孔隙结构分形维数反映混合料的堆积密实程度,分形维数越大,结构越密实,混合料配比越优。根据上述分析,选择废石与河砂配比(质量比)为5∶5,6∶4和7∶3,即废石质量分数分别为50%,60%和70%时,充填体强度实验结果最佳。
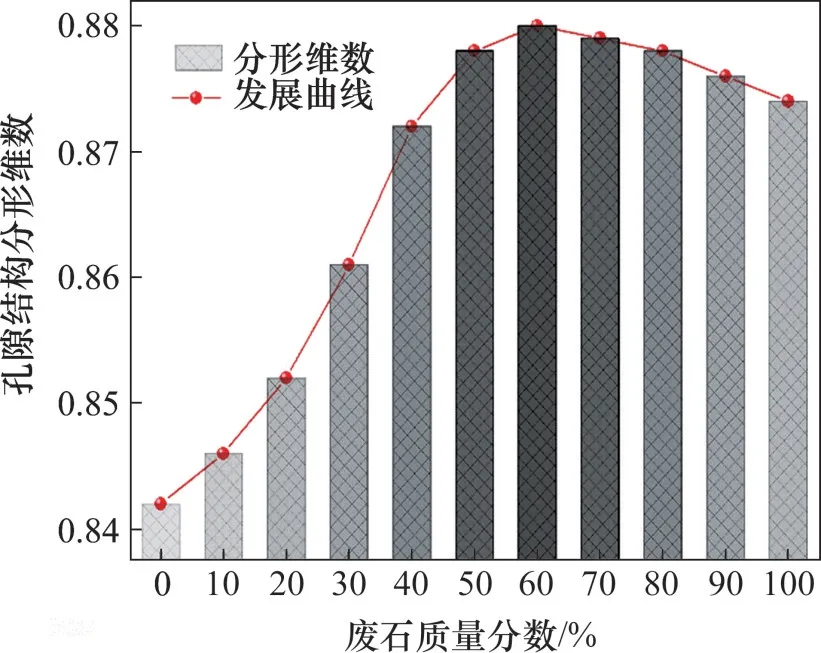
图2 不同配比混合骨料孔隙结构的分形维数Fig.2 Fractal dimension of pore structure of mixed aggregate with different proportions
2 响应面法优化充填体强度实验
2.1 响应面法实验设计
响应面法(response surface methodology,RSM)是利用合理的实验设计优化实验结果的一种方法,与常用的正交实验相比,可减少实验次数,提高实验效率与精度。本文采用Design-Expert 软件的Box-Behnken(BBD)进行响应面法计算[17-18]。
充填料浆配合比决定充填体强度,因此,本文以料浆质量分数、废石质量分数、水泥掺量3个影响因素为自变量(分别用X1,X2和X3表示),以充填体3 d,7 d和28 d抗压强度为响应值(分别用Y1,Y2和Y3表示),研究配合比各变量及其交互作用对充填体强度的影响。采用分级理论确定的废石质量分数50%~70%进行大量探索性实验,发现当充填料浆质量分数为78%~82%、水泥掺量为240~280 kg/m3时,强度与流动性均满足要求。因此,各变量取值如下:料浆质量分数为78%,80%和82%;废石质量分数为50%,60%和70%;水泥掺量为240,260 和280 kg/m3。RSM-BBD 实验因素与水平见表2。

表2 RSM-BBD实验因素与水平Table 2 RSM-BBD experimental factors and levels
2.2 实验结果与强度模型
RSM-BBD 实验结果见表3。使用Design-Expert软件对表3中的17组实验数据进行多元非线性拟合,建立不同养护龄期充填体抗压强度与料浆质量分数、废石质量分数、水泥掺量关系的响应模型,见式(9)~(11)。
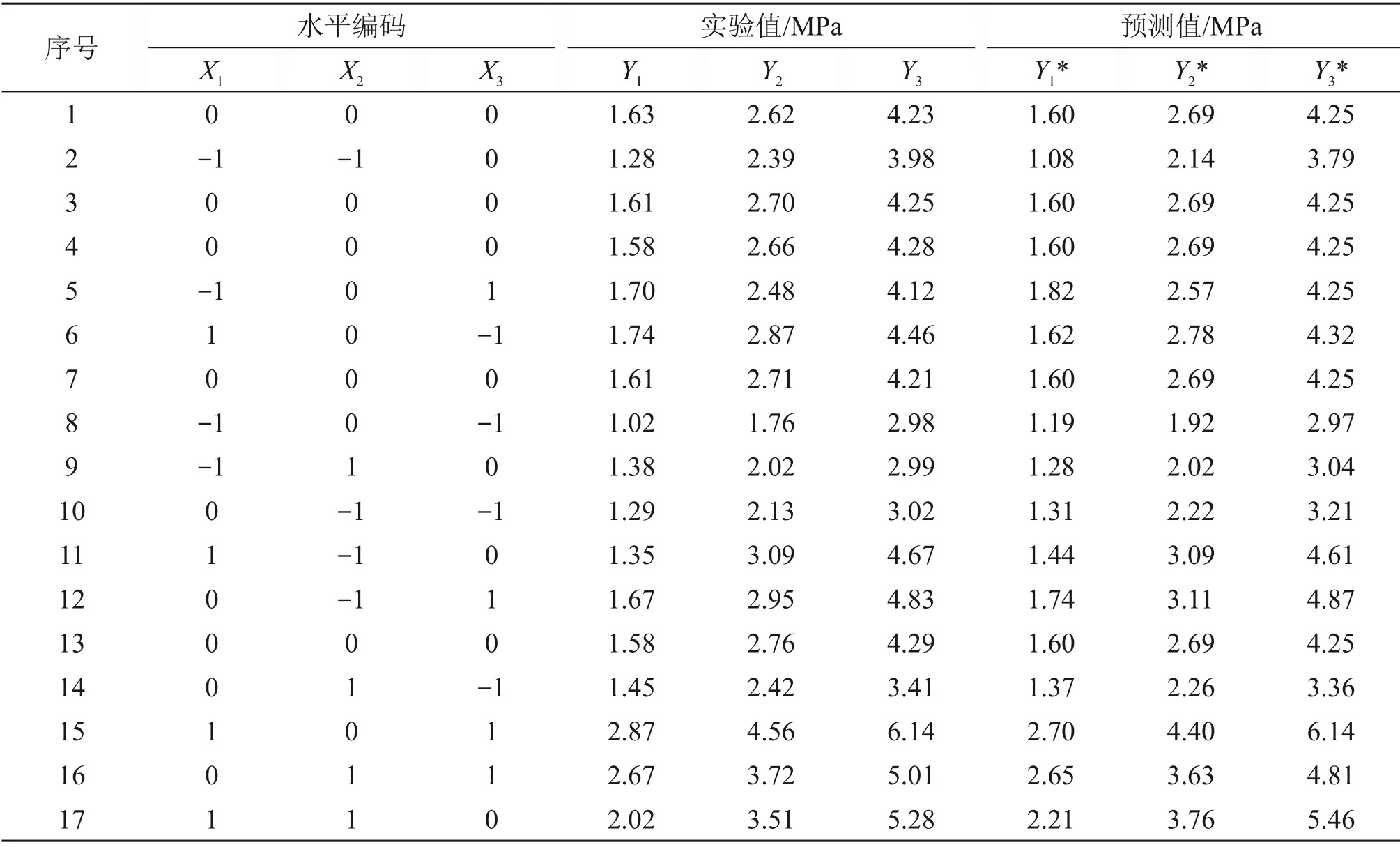
表3 RSM-BBD实验结果Table 3 Experimental results of RSM-BBD

式中:R2为相关系数。
2.3 强度回归模型可靠性分析
为了分析基于响应面法建立的强度模型是否有效,对上述回归方程进行方差分析,结果见表4。由表4 可知:本文所建强度模型的显著性检验P<0.01,极显著,表明模型具有较高的可靠度,进一步证明模型的可靠性。模型的相关系数R2趋近于1,表明模型的拟合性较好;模型的F检验最小值F=12.98,大于F0.05(3,13)(即3.41),表明该模型显著且具有统计学意义,能较好地反映充填体抗压强度与各影响因素的关系。图3所示为基于该强度模型计算的充填体强度与实验值的比较。从图3可以看出实验值与预测值吻合度较高,说明强度模型是有效的。
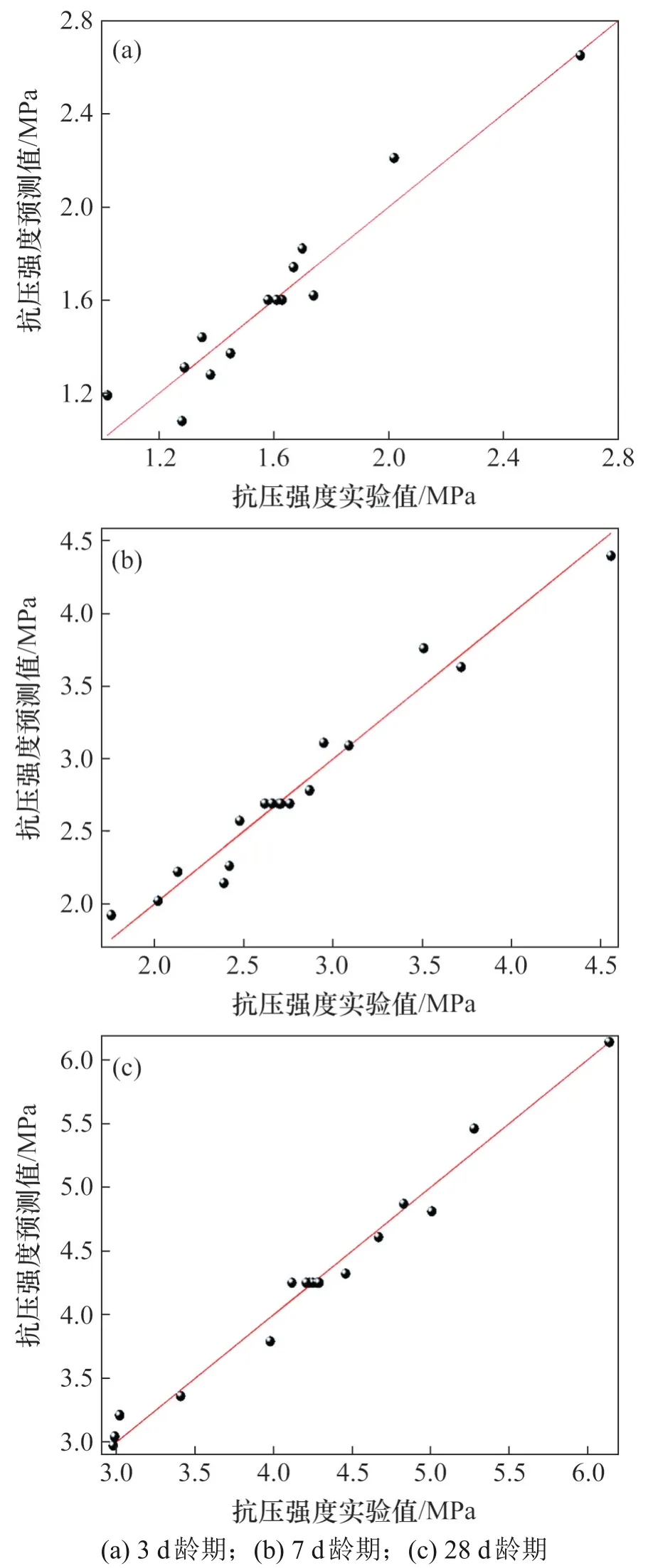
图3 充填体强度实验值与预测值比较Fig.3 Comparison between experimental value and predicted value of backfill strength
3 实验结果分析
3.1 响应面单因素对充填体强度的影响
由表4可知:料浆质量分数以及水泥掺量单因素对充填体全养护龄期内的抗压强度影响极显著,P<0.01;废石质量分数对3 d 龄期的早期充填体强度影响显著,对中后期充填体强度影响较弱,P>0.05。
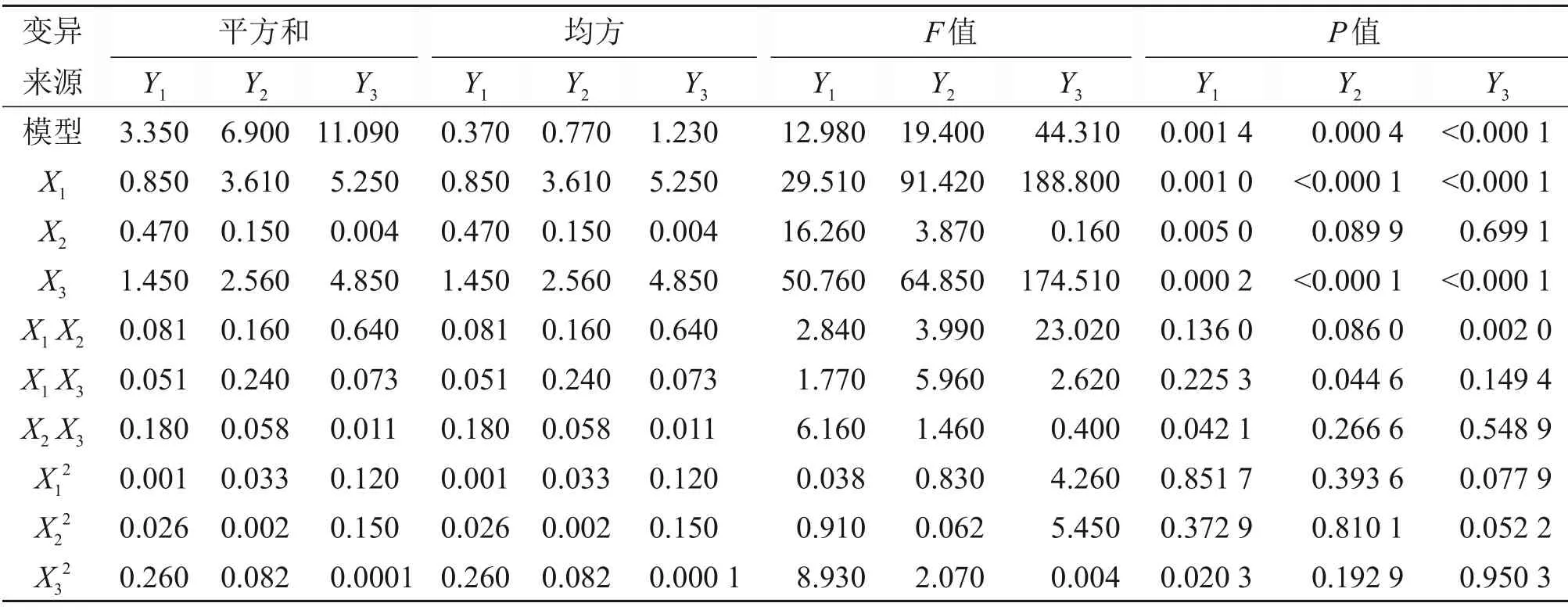
表4 响应面回归模型方差分析Table 4 Variance analysis of response surface regression model
3.1.1 水泥掺量对充填体强度的影响
当料浆质量分数为80%和废石质量分数为60%时,水泥掺量与充填体强度的关系见图4(a)。由图4(a)可知:随着水泥掺量增加,充填体各养护龄期强度显著提高;当水泥掺量由240 kg/m3增加到280 kg/m3时,充填体3 d、7 d 和28 d 强度分别提高60%,50%和45%;水泥掺量每提高10 kg/m3,对应龄期充填体强度分别提高0.21,0.28 和0.39 MPa。水泥作为充填料浆中的胶凝材料,通过水化反应生成C-S-H 凝胶、Ca(OH)2晶体和Aft 晶体等物质,这些物质填充骨料间的孔隙使充填体由疏松的孔隙结构转变为致密胶结结构,是充填体强度的主要来源。C-S-H 凝胶生成于水化反应各阶段,Aft 晶体主要在早期生成,Ca(OH)2晶体主要在中后期生成;水泥掺量的提高增加了各龄期不同产物的生成量,从而提高了各龄期充填体强度。
3.1.2 料浆质量分数对充填体强度的影响
当水泥掺量为240 kg/m3和废石质量分数为60%时,料浆质量分数与充填体强度的关系见图4(b)。由图4(b)可知:随着料浆质量分数提高,充填体强度呈逐渐增大的趋势,且料浆质量分数越高,强度提升越显著;料浆质量分数由78%提高到82%,充填体3 d、7 d 和28 d 强度分别提高36%,45%和45%,即料浆质量分数对充填体中后期强度的提升作用强于对早期强度的提升作用,这与表4中的P值分析结果一致。料浆质量分数的提高增加了充填料浆的黏度,使骨料在料浆中的沉降阻力增大,降低了泌水和粗细骨料的分层离析,骨料的分布更加均匀,从而提高了充填土强度;早期骨料的沉降离析作用不明显,因而料浆质量分数对充填体中后期强度的提升作用比对早期强度的提升作用强。此外,在水泥与骨料掺量不变的前提下,料浆质量分数提高意味着水的占比减少,使水泥浆基体和粗骨料间过渡区的孔隙率变小,骨料间黏结力增大,充填体强度提高。
3.1.3 废石质量分数对充填体强度的影响
当水泥掺量为240 kg/m3和料浆质量分数为80%时,混合料中废石质量分数与充填体强度的关系见图4(c)。由图4(c)可知:随着废石质量分数提高,充填体强度先增大后减小;当废石质量分数小于60%时,充填体强度随废石质量分数提高而增大;当废石质量分数为60%时,充填体强度达到最大值;当废石质量分数大于60%时,充填体强度逐渐减小。这一结果与混合骨料分形维数的计算结果一致,即当废石质量分数为60%时骨料分形维数最大,骨料结构最密实,因而,此时的充填体强度最高,表明基于分形理论优化骨料配比来提高充填体强度的方法是可行的。
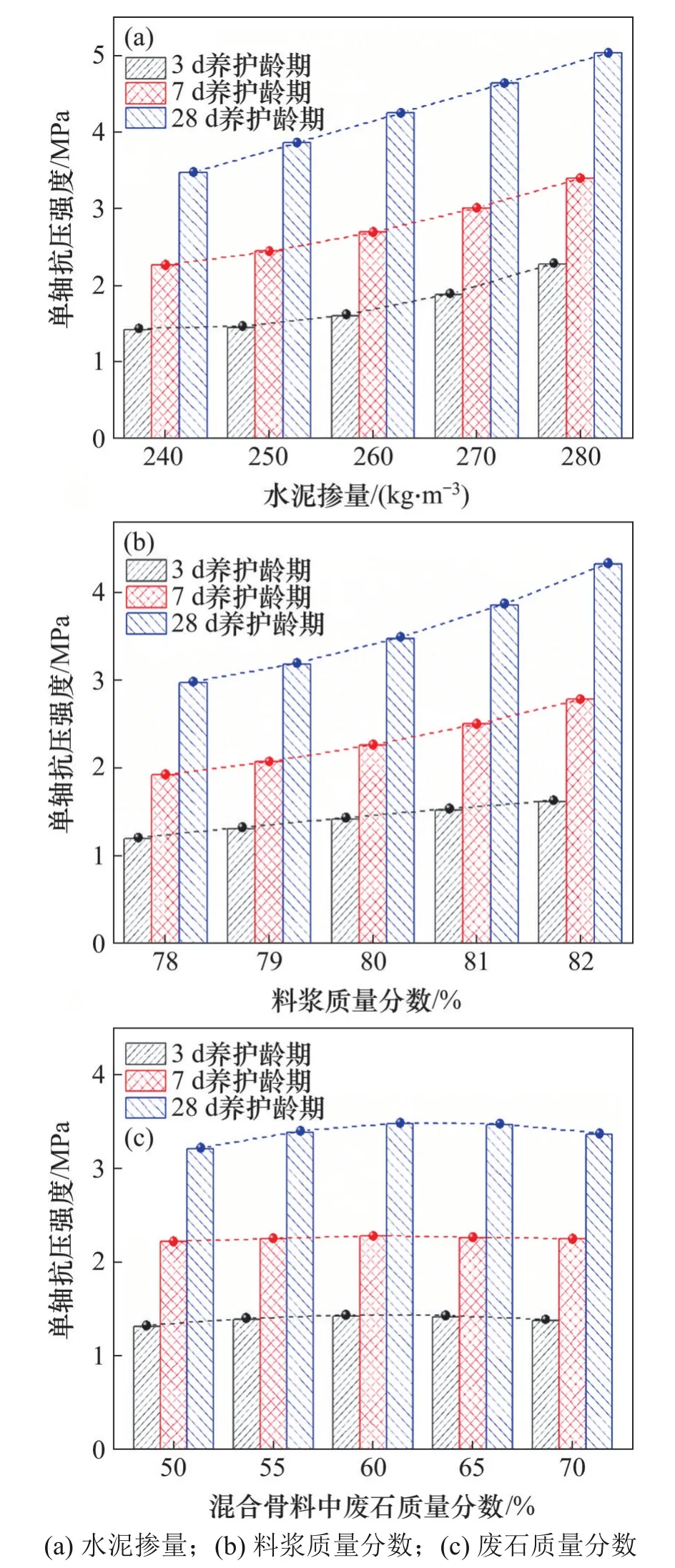
图4 单因素对充填体强度的影响Fig.4 Influence of single factor on strength of filling body
3.2 响应面各因素交互作用对充填体强度的影响
由表4 可知:充填体强度不仅受单因素的影响,而且还受到各因素交互作的影响。混合料中废石质量分数与水泥掺量交互作用对充填体3 d强度影响显著,P<0.05;料浆质量分数与水泥掺量交互作用对充填体7 d 强度影响显著,P<0.05;废石质量分数与料浆质量分数交互作用对充填体28 d强度影响显著,P<0.01。
图5所示为混合料中废石质量分数与水泥掺量交互作用对充填体3 d 强度的影响。由图5 可知:当混合料中废石质量分数为50%时,水泥掺量由240 kg/m3提高到280 kg/m3,充填体3 d 强度提高33%;当混合料中废石质量分数为60%时,水泥掺量由240 kg/m3提高到280 kg/m3,充填体3 d强度提高61%,几乎是前者的2倍。由此可知,良好的骨料配比可以显著提高水泥的胶凝作用。在充填体强度发育早期,胶凝物质生成量少,若混合骨料配比不当,则会使充填体结构松散,胶凝物质无法充分充填孔隙,导致强度降低;当混合骨料配比适宜时,颗粒间形成嵌锁结构,少量胶凝物质充填即可使充填体具备一定的早期强度[8]。
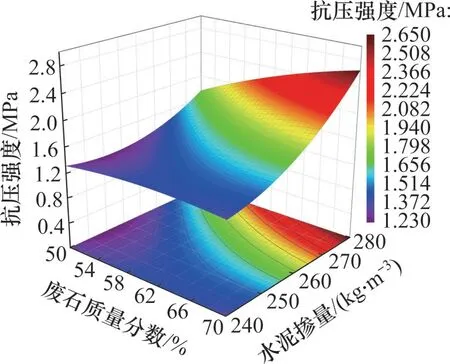
图5 废石质量分数与水泥掺量对充填体强度的影响Fig.5 Influence of waste rock mass fraction and cement content on strength of backfill
图6所示为料浆质量分数与水泥掺量交互作用对充填体7 d 强度的影响。由图6 可知:提高料浆质量分数与水泥掺量均可显著提高充填体7 d 强度;当料浆质量分数为78%时,水泥掺量由240 kg/m3提高到280 kg/m3,充填体7 d强度提高34%;当料浆质量分数为82%时,水泥掺量由240 kg/m3提高到280 kg/m3,充填体7 d强度提高58%。可见,随着料浆质量分数提高,水泥掺量对充填体7 d强度的提升作用明显加强。同时,高水泥掺量下料浆质量分数对充填体7 d强度的提升作用明显比低水泥掺量的提升作用强。因此,料浆质量分数与水泥掺量交互作用表现为互相激发对中期强度的增强特性。在充填体强度发育中期,料浆质量分数高时混合骨料未发生沉降离析,大量胶凝物质将骨料胶结在一起,使充填体具有较高的中期强度[11]。
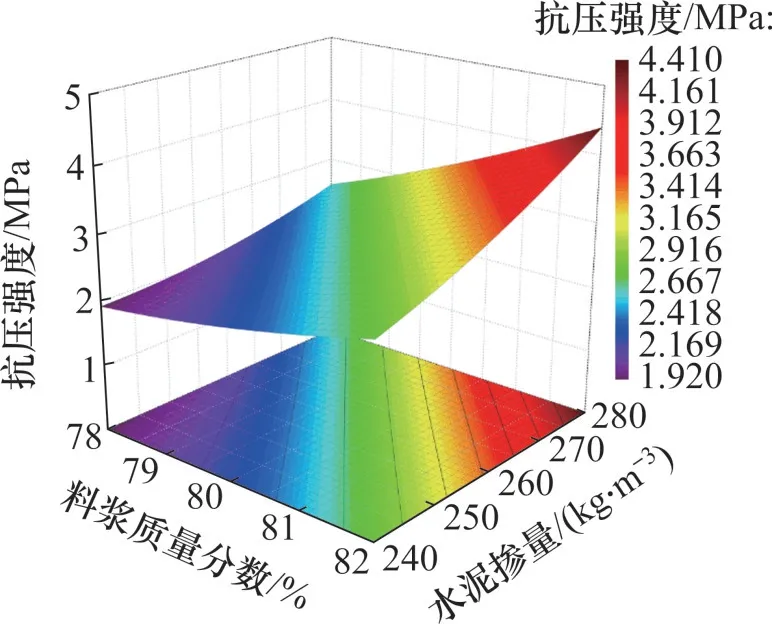
图6 料浆质量分数与水泥掺量对充填体强度的影响Fig.6 Influence of slurry mass fraction and cement content on strength of backfill
图7所示为料浆质量分数与废石质量分数交互作用对充填体28 d强度的影响。由图7可知:在任意废石质量分数下,充填体28 d 强度均随着料浆质量分数提高而提高;在任意料浆质量浓度下,充填体28 d 强度随着废石质量分数提高先增大后减小;当废石质量分数为50%时,料浆质量分数由78%提高到82%,充填体28 d 强度提高22%;当废石质量分数为60%时,料浆质量分数由78%提高到82%,充填体28 d强度提高46%;在良好的混合骨料级配作用下,料浆质量分数对充填体28 d强度的提升作用加强;当废石质量分数为60%,料浆质量分数较高时,充填体具有较高强度。料浆质量分数决定了浆体中的混合骨料配比,而废石质量分数决定了混合骨料配比的性能,在骨料配比良好的条件下,通过提高料浆质量分数来达到降低骨料离析的目的,两者交互作用,促进了后期充填体强度发展[9]。
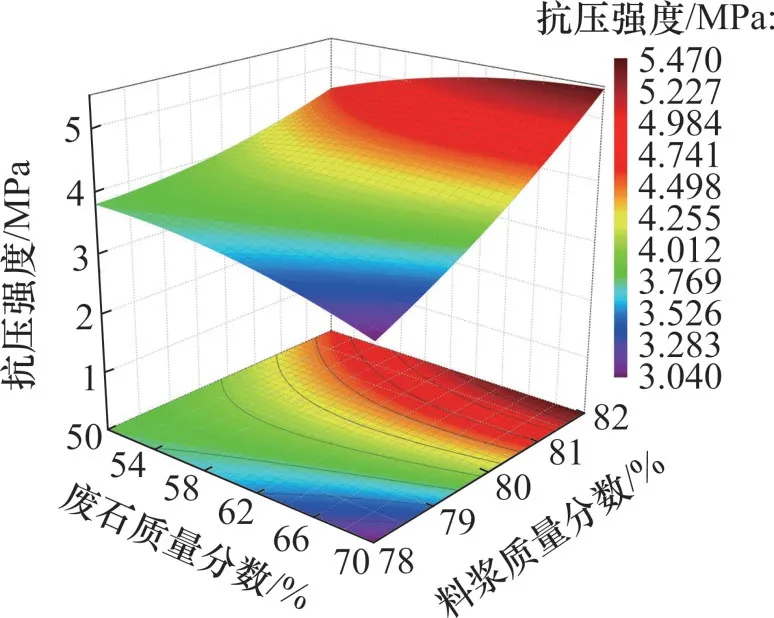
图7 料浆质量分数与废石质量分数对充填体强度的影响Fig.7 Influence of slurry mass fraction and waste rock mass fraction on strength of backfill
4 混合骨料充填配比多目标优化
4.1 构建RSM-BBD-DF多目标优化算法
确保不同养护龄期的充填体强度满足矿山充填要求,对井下安全生产至关重要,但若充填体强度过高,则会不可避免地增加充填采矿的成本,因此,只有当充填体强度超过且接近矿山要求标准值时,才能确保井下的安全、高效回采。本文基于RSM-BBD实验法构建不同充填体强度的响应模型,但对于多个响应值无法同时开展优化计算,因此,考虑结合充填体强度响应模型采用基于满意度准则的多目标优化算法(DF)进行求解[19-20],即构建RSM-BBD-DF多目标求解算法模型。
根据不同强度的响应模型,构建如下单满意度函数:
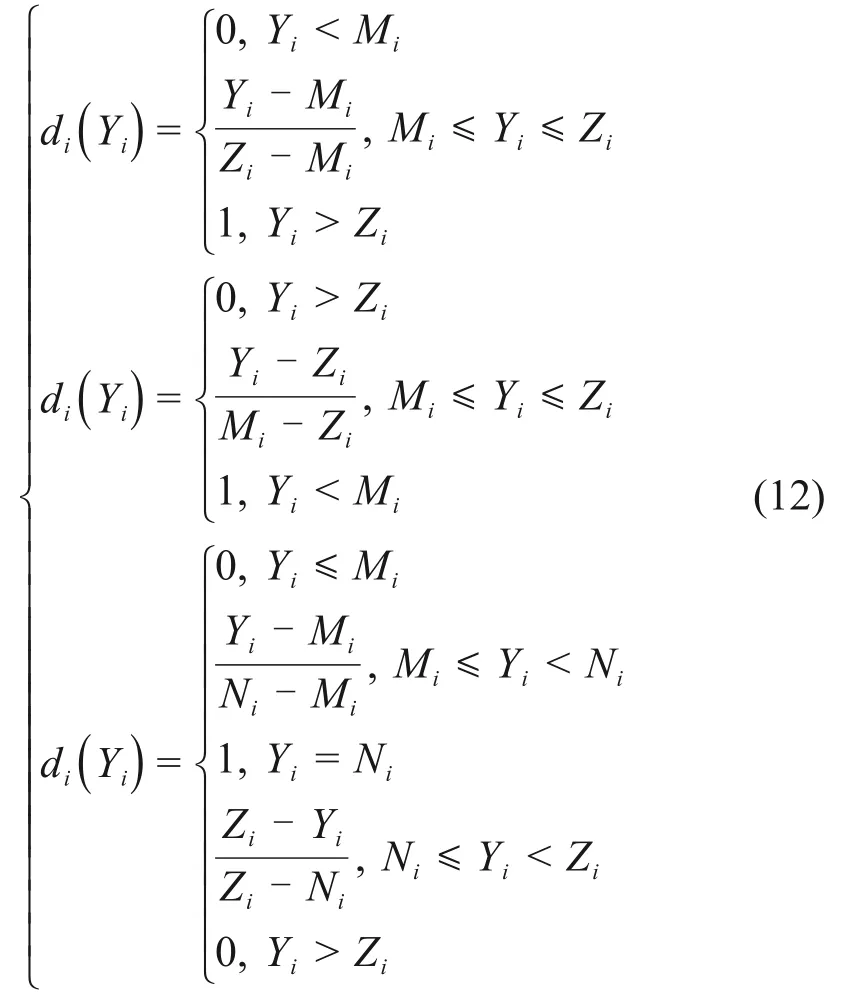
式中:di为第i个响应面的满意度函数;Yi为第i个响应值(根据RSM-BBD 法构建的强度响应模型计算得到);Mi,Zi和Ni分别为第i个响应值的下限、上线和最优目标值。
根据不同的优化目的(响应最大值、最小值或目标值),选择对应的单满意度函数进行计算,基于计算结果建立各单满意度函数加权几何平均多目标优化函数[21],即整体满意度函数:
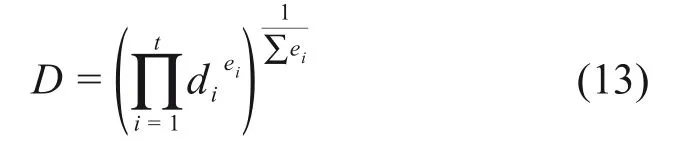
式中:t为响应值数量;ei为权数,取决于不同响应值在充填配比优化中的重要程度。
RSM-BBD-DF 多目标优化法,即以需要优化得到的目标值作为响应值Yi,以影响目标值的变量作为影响因素Xi,通过开展中心复合实验得到相关响应值与影响因素的关系,并构建响应面回归模型,以该回归模型为基础构建单满意度函数di(Yi),通过计算不同Xi下的单满意度函数将不同Yi转化为0~1范围内的数,进而通过整体满意度函数寻求最优解,实现多目标优化的目的。RSM-BBD-DF 多目标优化法寻优过程如图8所示。
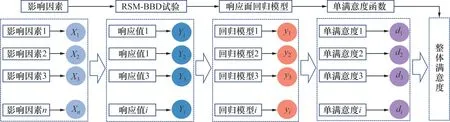
图8 RSM-BBD-DF多目标优化法寻优过程Fig.8 Optimization processes of RSM-BBD-DF multi objective optimization method
4.2 混合骨料充填配比多目标优化
采用机械化盘区下向分层水平进路充填采矿法对金川二矿区进行开采,要求充填体强度为3 d、7 d 和28 d 的强度分别不低于1.5 MPa、2.5 MPa 和5 MPa。根据RSM-BBD实验结果,将3 d强度的优化范围定为1.5~2.5 MPa,优化目标值定为1.5 MPa;将7 d强度的优化范围定为2.5~4.0 MPa,优化目标值定为2.5 MPa;将28 d 强度的优化范围定为5.0~6.5 MPa,优化目标值定为5.0 MPa。根据金川二矿区充填采矿法的采矿工艺,不同养护龄期充填体强度的重要性从大到小排序为28 d,7 d和3 d,因此,将强度响应值对优化目标的权值分别定为0.5,0.3和0.2,故取e1=5,e2=3,e3=2。
根据式(12)和(13)对充填体强度的单满意度和整体满意度进行计算,得到单因素对单满意度的影响规律及多因素影响下整体满意度,分别见图9(a)和9(b)。由图9(a)可知:料浆质量分数对充填体强度的单满意度影响极显著,料浆质量分数越高,充填体强度的单满意度越大;废石质量分数对充填体强度的单满意度的影响较小,满意度处于0.47~0.60 的范围内,废石质量分数在64%~68%范围内,充填体强度的单满意度最大;水泥掺量对充填体强度的单满意度影响较显著,充填体强度满意度处于0.14~0.66 范围内;当水泥掺量为250 kg/m3左右时,充填体强度单满意度最大。基于上述分析,取料浆质量分数为81%~82%,水泥掺量为240~260 kg/m3,以废石质量分数为变量计算多因素下的整体满意度,结果见图9(b)。由图9(b)可知:当料浆质量分数为82%、废石质量分数为66%和水泥掺量为250 kg/m3时,充填体强度整体满意度具有最大值为0.98。
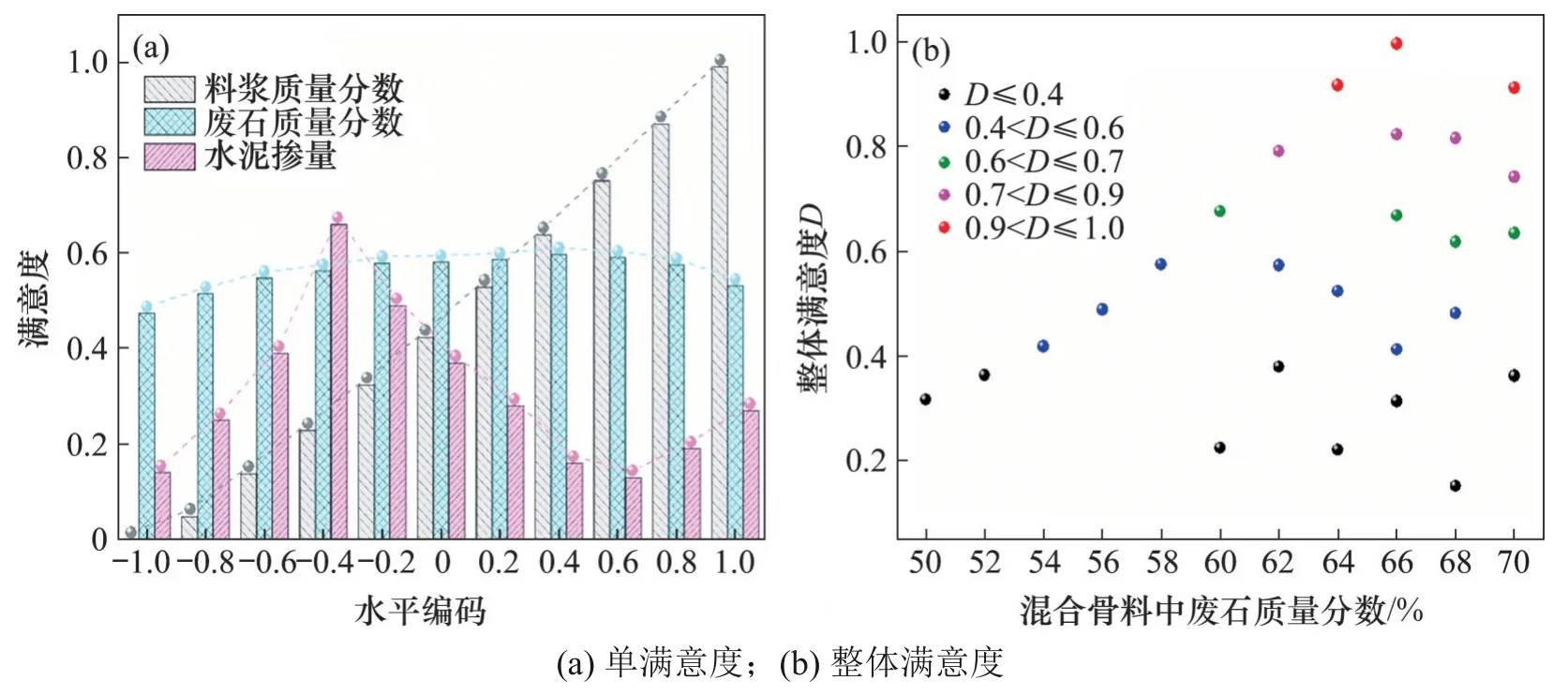
图9 不同条件下的满意度计算结果Fig.9 Satisfaction calculation results under different conditions
为验证RSM-BBD-DF 法得到的充填配合比强度是否满足要求,采用前述配合比进行室内试验,得到3 d、7 d 和28 d 抗压强度,均满足强度要求。可见,该强度优化方法可靠性较高,可用于矿山的充填配合比设计与优化。充填体强度验证结果见表5。

表5 充填体强度验证结果Table 5 Strength verification results of backfill
5 结论
1)基于Talbol 理论对混合骨料开展集配分析,河砂级配指数为0.339,低于0.500,说明河砂细粒级占比偏大,需要添加粗骨料进行优化;废石破碎集料级配指数为0.651,高于0.500,说明废石粗粒级占比偏大,需要添加细骨料改善级配。
2)采用分形理论构建了混合料孔隙结构分形维数计算模型。孔隙结构分形维数反映了混合料的堆积密实程度,分形维数越大,结构越密实,混合料配比越优;随着废石集料在混合料中占比增大,混合料孔隙结构分形维数呈先增大后减小的趋势,当废石质量分数为60%时,分形维数最大,混合料最密实。
3)基于响应面法构建了充填体强度回归模型,分析表明充填体强度不仅受单因素的影响,而且受各因素交互作的影响。废石质量分数与水泥掺量交互作用对充填体3 d强度影响显著;料浆质量分数与水泥掺量交互作用对充填体7 d强度影响显著;废石质量分数与料浆质量分数交互作用对充填体28 d强度影响显著。
4)基于满意度准则的多目标优化算法得到了满足强度要求的最佳配合比:料浆质量分数为82%,废石质量分数为66%,水泥掺量为250 kg/m3。利用该配比开展室内试验得到强度实验值均满足矿山强度要求。研究结果可为同类型充填配合比优化提供指导。
