高速铁路无砟轨道-桥梁系统纵向变形与轨面变形映射关系

2022-03-29赖智鹏蒋丽忠

中南大学学报（自然科学版） 2022年2期

赖智鹏，蒋丽忠,2

(1.中南大学土木工程学院，湖南长沙，410075；2.高速铁路建造技术国家工程实验室，湖南长沙，410075)

高速铁路桥梁在遭受如地震等极端荷载时，桥墩和支座等构件将会损伤甚至破坏[1]，这些构件的损坏或破坏会导致相应的桥梁残余变形[2]，例如墩台沉降[3]、梁端转角以及梁体错台位移。同时，高速铁路桥梁经过多年的运营使用，混凝土的蠕变和混凝土强度的下降也会引起桥梁的变形。桥梁变形通过桥梁和轨道的共同作用最终反映至轨面，形成附加轨道不平顺[4]。轨道几何形态的恶化将对列车行驶的舒适性甚至安全性构成极大的威胁[5]。因此，找到一种有效的方法来评估桥梁变形对轨道几何形态变化的影响十分重要。

在铁路工程实践中，一般通过铁路轨检列车测量来获得铁路轨道不平顺样本，基于经典谱估计理论建立相应轨道不平顺谱。为了提高准确性和效率，许多新技术被用于测量铁路轨道几何不平顺，例如人工神经网络[6-7]。由于轨道不平顺对列车的动力响应有重大影响，因此，可以通过列车响应逆向获取轨道不平顺[8-9]，另外，相关学者也开展了利用其他数值方法评估轨道几何形态的研究[10-11]。

桥梁变形对轨道的不平顺状态影响极大，合理有效地建立桥梁变形与轨面变形的映射关系，量化轨面几何形态的变化，对我国无砟轨道建造以及运营管理意义重大。解析方法能直观、简洁及有效地评估桥梁变形下轨道几何形态[12]，目前已有不少相关报道。魏亚辉等[13-14]基于弹性支撑梁模型以及室内试验，研究了桥梁竖向梁端变形对扣件内力以及钢轨应力研究。陈兆玮等[15-16]基于力学平衡关系，针对单元板式以及纵连板式无砟轨道开展了映射关系研究，分析了桥梁竖向变形对无砟轨道几何形态影响。郭宇等[17]基于解析和有限元模型研究了路基沉降下的板式无砟轨道映射变形。GOU等[18-19]提出了桥梁竖向、横向变形下单元板式无砟轨道的映射变形求解模型，并评估了桥梁变形幅度、扣件刚度和砂浆层刚度对轨道映射变形的影响。ZENG等[20]对桥隧过渡处梯度温度力作用下的钢轨纵向变形展开了研究。单元板式无砟轨道中轨道板和底座纵向不连续，因此轨道与桥梁的相互作用较弱，轨道变形与桥梁变形跟随性良好[21]。然而，由于纵连式无砟轨道纵向连续，轨道板和底座板等对桥梁存在较强的约束作用，轨道变形与桥梁变形的跟随性变差[4]。目前关于桥梁变形与轨道变形之间的映射关系研究均假设桥梁位移保持线性，忽略轨道对桥梁的约束作用，分析轨道纵连作用对桥梁变形下轨道几何形态的影响的研究较少。

为系统分析高速铁路桥梁纵向变形对轨道几何形态的影响，本文作者综合考虑HSRTBS 层间传力机制，将轨道-桥梁系统层间构件分离，基于层间内力平衡条件，采用能量变分原理建立桥梁纵向变形影响下的轨道映射变形求解模型，并建立相应有限元数值模型验证。最后，进一步分析HSRTBS结构参数对轨面映射变形的影响规律。

1 桥梁纵向变形与CRTSII 型无砟轨道映射变形

CRTSII 型纵连式无砟轨道是我国具有自主知识产权的纵连式无砟轨道，在我国高速铁路线路中应用广泛。CRTSII 型无砟轨道与桥面之间的连接主要通过剪力齿槽及侧向挡块，同时轨道结构与桥面层间布置有“两布一膜”，形成滑动层。CSRTSII 型无砟轨道结构主要组成部分有：钢轨、弹性扣件、预制轨道板、水泥乳化沥青(CA)砂浆填充层、剪切钢筋、底座板、滑动层、剪力齿槽、侧向挡块等，图1 所示为中国高速铁路CRTSII 型纵连式无砟轨道在简支梁桥上的布置形式。

图1 高速铁路简支梁桥上CRTSII型无砟轨道布置形式Fig.1 Layout of CRTSII track on high-speed rail bridge

分析HSRTBS 传力机制可知，在桥梁发生纵向变形时，将通过滑动层及剪力齿槽传递至轨道结构，然后继续通过轨道层间连接构件传递至轨面。参考文献[4]所建立理论模型，对HSRTBS 进行力学建模时，假设：1) 将CRTSII 型轨道-桥梁系统的层间连接线性均匀化为离散弹簧，典型构件包括：扣件、CA砂浆层、滑动层以及滑动层内剪力齿槽、CA 层内剪切钢筋等层间局部加强构件；2)考虑轨道结构在两侧路基段有充足的延伸距离，并将延伸段轨道端点假设为简支。

1.1 轨道构件力学模型

钢轨力学模型如图2所示，其中，路基延伸段左端端点为坐标原点，沿钢轨纵向为X方向，第i个扣件在整体坐标中位置为Xi，扣件内力为fur-s,i，桥梁段扣件总数量为N1，左右路基延伸段扣件总数量均为N2，路基延伸段和桥梁段总长度为L。将钢轨从轨道-桥梁系统分离，此时扣件力于钢轨而言可视为外荷载，当仅考虑桥梁纵向变形的影响时，可认为扣件仅产生X方向的内力。

图2 钢轨力学模型Fig.2 Mechanical model of rail

记钢轨的纵向位移及其一阶导数分别为U1和可将钢轨的能量泛函Π1表示为

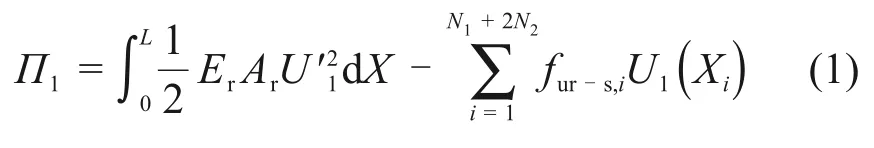
式中，Er和Ar分别为钢轨弹性模量和截面面积。

由于路基延伸段上钢轨端点边界假设为简支，基于里兹法可假设钢轨纵向位移U1为

式中：Aum为钢轨纵向位移系数；m为正弦函数序列阶数。

由能量变分原理，δΠ1= 0，求得钢轨纵向位移系数Aum并代入式(2)，可以求得钢轨纵向位移为

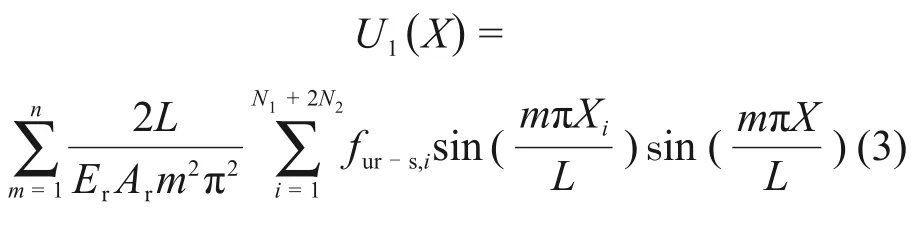
根据式(3)，所有扣件位置处的钢轨纵向位移向量Q为

式中：R为钢轨位移系数矩阵，R中第i行第k列元素为扣件力向量。

轨道板力学模型如图3 所示，图中，fus-b,i为CA砂浆层内力。将轨道板从轨道-桥梁系统分离，此时扣件力和CA砂浆层内力于轨道板而言，可视为外荷载。

图3 轨道板力学模型Fig.3 Mechanical model of track slab

在桥梁纵向变形影响下，轨道板的静态总势能主要包括轨道板轴向拉压势能、扣件力以及CA砂浆层内力做的外力功，记轨道板弹性模量和截面面积分别为Es和As，轨道板纵向位移及其一阶导数分别为U2和轨道板能量泛函Π2可表示为

由于轨道板纵向连续，路基延伸段上轨道板端点边界假设为简支，基于里兹法可假设轨道板纵向位移为

式中：Bum为轨道板纵向位移系数。

由能量变分原理，δΠ2= 0，求得轨道板纵向位移系数Bum并代入式(6)可得：

根据式(7)，所有扣件位置的轨道板纵向位移向量A为

其中：C为轨道板位移系数矩阵，C中第i行第k列元素K为CA砂浆层内力向量。

底座板力学模型如图4所示，图中，fub-b,i为滑动层内力。将底座板从轨道-桥梁系统分离，此时相对于底座板而言，CA砂浆层内力和滑动层内力可视为外荷载。

图4 底座板力学模型Fig.4 Mechanical model of track base

在桥梁纵向变形影响下，底座板的静态总势能主要包含底座板轴向拉压势能、CA砂浆层内力和滑动层内力做的外力功，记底座板弹性模量和截面面积分别为Etb和Atb，底座板纵向位移及其一阶导数分别为U3和可得底座板能量泛函Π3为

由于底座板纵向连续，路基延伸段上底座板端点边界假设为简支，基于里兹法可假设底座板纵向位移为

式中：Cum为底座板纵向位移系数。

由能量变分原理，δΠ3= 0，求得底座板纵向位移系数Cum，并代入式(10)可得：

所有扣件位置的底座板纵向位移向量Z为

其中：S为底座板位移系数矩阵，S中第i行第k列元素为滑动层内力向量。

1.2 桥梁纵向力学模型

桥梁力学模型如图5所示。将单跨桥梁从轨道-桥梁系统中分离考虑，每跨桥梁的纵向外荷载仅有滑动层内力。

图5 桥梁力学模型Fig.5 Mechanical model of a bridge

每跨桥梁的静态总势能主要包括桥梁的轴向拉压势能以及滑动层内力做的外力功。记第j跨桥梁主梁的局部坐标为xj，原点设置在桥梁主梁左边梁端。各跨桥梁的能量总泛函Π4可以表示为

式中：lb为主梁长度；nb为桥梁跨数；n1为桥梁范围内等效滑动层弹簧数量；Eb和Ab分别为桥梁主梁弹性模量和截面面积；uj为第j跨桥梁主梁纵向位移。

考虑支座处纵向变位时，基于里兹法，结合简支梁桥边界条件，第j跨桥梁主梁轴向拉压变形可表示为

因此，第j跨桥梁主梁纵向位移可表示为

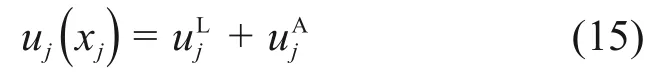
式中：为第j跨桥梁主梁的线性纵向位移。

基于能量变分原理，δΠ4= 0，求得每跨位移系数Dum,j并代入式(15)，可得第j跨桥梁主梁纵向位移为

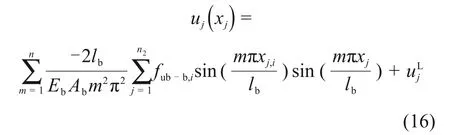
当所有桥梁跨度一致时，令xj=。根据局部坐标xj与总体坐标X之间的关系，可求得总体坐标下桥梁主梁纵向位移U4为

式中：lbb为相邻两跨主梁之间的间距，LR为左路基延伸段长度。

总体坐标下所有扣件位置的桥梁纵向位移向量W为

1.3 纵向映射关系建立

在桥梁纵向变形影响下，HSRTBS中扣件力向量J为

式中：扣件的弹簧刚度为ku-r。

联立式(4)，(8)和(19)，可得：

式中：E表示维数为(N1+ 2N2)×(N1+ 2N2)的单位矩阵。

在桥梁纵向变形影响下，HSRTBS 中CA 砂浆层内力向量K为

式中：ku-ca为CA砂浆层的弹簧刚度。

在桥梁主梁梁端上方的CA砂浆层内均布置了剪切钢筋，第l个剪切钢筋在总体坐标中的位置为Xl，剪切钢筋的影响通过乘以剪切钢筋转换矩阵M考虑，则第l个剪切钢筋的影响用转换矩阵的分量Ml表示：

式中：ksb为剪切钢筋刚度。

联立式(8)，(12)，(21)和(22)，可得

在桥梁纵向变形影响下，滑动层内力向量Ls可表示为

式中：ku-h为滑动层的弹簧刚度。

由于在桥梁固定支座上方的桥面布置了剪力齿槽，第t个剪力齿槽在总体坐标中的位置为Xt，因此，需对滑动层刚度做相应修正。将滑动层相应位置的弹簧刚度替换为ks，剪力齿槽的影响通过乘以剪力齿槽转换矩阵T考虑，则第t个剪力齿槽的影响用转换矩阵的分量Tt表示：

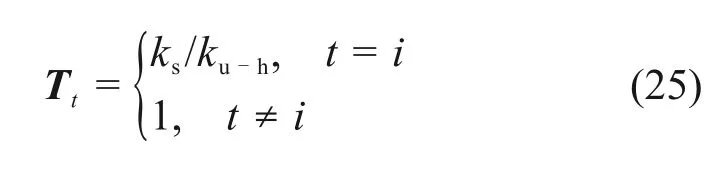
其中：ks为剪力齿槽的弹簧刚度。

联立式(12)，(18)，(23)，(24)和(25)，可求得滑动层内力向量Ls为

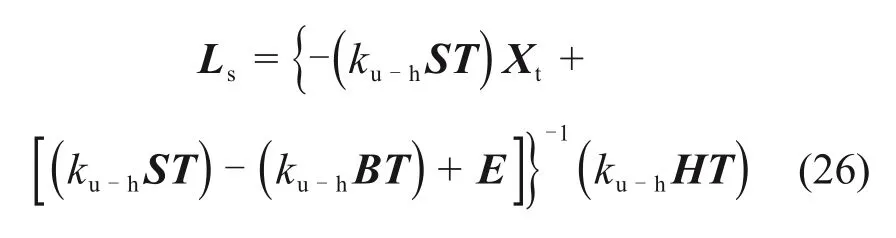
将Ls代入式(23)和(20)，可求得CA 砂浆层纵向内力K和扣件内力J，然后根据(4)可求得轨面纵向映射位移。

2 数值算例验证

选取7跨32 m简支梁桥和CRTS II纵连式无砟轨道作为研究对象，基于ANSYS有限元软件建立相应数值模型，CRTSII轨道-桥梁系统有限元模型示意图如图6所示。其中，路基上轨道延伸段左端点为坐标原点，桥梁主梁采用梁单元模拟，桥梁主梁两端通过约束纵向和横向自由度来模拟简支条件；钢轨、轨道板、以及底座板采用梁单元模拟，滑动层、CA砂浆层、扣件以及剪力齿槽、剪切钢筋均采用线性弹簧模拟。路基段忽略自身变形，采用空间固结点模拟，路基长度取250 m；路基上轨道延伸段端点约束纵向以及横向自由度来模拟简支条件。轨道-桥梁系统模型的结构参数取值如表1所示。

图6 CRTSII轨道-桥梁系统有限元模型示意图Fig.6 Schematic diagram of FE model for CRTSII track-bridge system

表1 CRTSII型轨道-桥梁系统结构参数Table 1 Structural parameters of CRTSII track-bridge system

图7所示为第四跨桥梁纵向平动下钢轨位移的映射解和有限元解的对比。从图7可见：位移映射解和有限元解吻合良好，钢轨位移的有限元解和映射解最大相对误差为0.67%。有效验证了本文解析模型的有效性及合理性。

图7 单跨桥梁平动下钢轨映射变形与有限元结果对比Fig.7 Comparison between mapping rail deformation under single girder translation and finite element results

3 CRTSII 型轨道-桥梁系统参数对钢轨纵向映射变形的影响

以第四跨桥梁纵向平动下钢轨映射位移变化为例，研究HSRTBS 结构参数对桥梁纵向变形下钢轨映射变形的影响，轨道-桥梁系统初始结构参数见表1，所有工况中桥梁纵向变形初始幅值均取5 cm。为直观有效地描述HSRTBS 结构参数对桥梁纵向变形下钢轨映射变形的影响，引入以下指标：1)桥梁纵向变形下钢轨映射变形的最大值UMRD，以X轴正向为正；2)钢轨纵向映射变形系数Rc=DLr/Lb，其中，DLr为钢轨纵向映射变形，Lb为桥梁纵向初始变形。

3.1 桥梁纵向初始变形幅值的影响

桥梁纵向初始变形幅值取5 cm，考虑桥梁纵向变形幅值缩放系数为0.2，0.4，1.0，2.0 和4.0时，对桥梁纵向变形下钢轨纵向映射变形的影响。图8所示为不同桥梁纵向变形幅值对钢轨的映射位移的影响。从图8可以看出，钢轨纵向映射位移随着桥梁变形幅值增大而增大。

图8 桥梁纵向变形幅值对钢轨映射变形的影响Fig.8 Influence of amplitude of longitudinal bridge deformation on mapping rail deformation

桥梁纵向变形幅值对钢轨映射变形峰值影响如图9所示。从图9可见：钢轨映射位移峰值与桥梁变形幅值成线性关系。桥梁纵向变形幅值对钢轨映射变形系数影响如图10 所示。从图10 可见：虽然钢轨映射变形随着桥梁变形幅值的增大而增大，但Rc与桥梁变形幅值呈非线性关系增长，随着桥梁变形幅值增大，钢轨映射变形增长速率逐渐变缓。

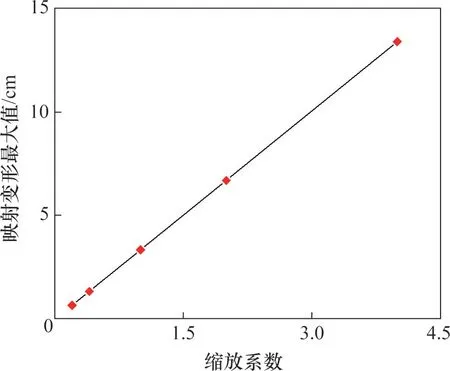
图9 桥梁纵向变形幅值对钢轨映射变形峰值影响Fig.9 Influence of amplitude of longitudinal bridge deformation on the maximum of mapping rail deformation

图10 桥梁纵向变形幅值对钢轨映射变形系数影响Fig.10 Influence of amplitude of longitudinal bridge deformation on the range of mapping rail deformation

3.2 扣件纵向刚度的影响

层间扣件刚度ku-r初始值为7.5 kN/mm，考虑层间扣件刚度缩放系数分别为0.01，0.1，1.0，10，和100 时，对桥梁纵向变形下钢轨纵向映射变形的影响，结果如图11～13所示。

图11 层间扣件刚度对钢轨纵向映射变形的影响Fig.11 Influence of fasten stiffness on mapping rail deformation

图12 层间扣件刚度对钢轨映射变形峰值影响Fig.12 Influence of fasten stiffness on the maximum of mapping rail deformation

图13 层间扣件刚度对钢轨映射变形系数影响Fig.13 Influence of fasten stiffness on range of mapping rail deformation

从图11～13可知，层间扣件刚度变化对钢轨纵向映射变形影响显著。当k′u-r/ku-r取0.01时，钢轨映射变形系数高达11.04，钢轨除了在所有桥跨上方产生纵向映射变形外，还在两侧路基延长段为2倍桥梁跨度的范围内也产生相应映射变形。当k′u-r/ku-r取0.1 时，钢轨映射变形系数为5.58，单跨桥梁的纵向变形可导致钢轨在6倍桥梁跨度范围内产生映射变形。当k′u-r/ku-r取值大于10 时，钢轨映射变形系数逐渐保持平稳，保持在3.35左右。区别于钢轨映射变形系数变化规律，钢轨映射变形峰值随着层间扣件刚度的增大而增大。当k′u-r/ku-r取0.01，0.1，10，100 时，钢轨映射位移峰值分别为考虑初始扣件刚度情况时UMRD的27.62%， 63.06%， 115.57% 和 119.32%，在k′u-r/ku-r取值大于1 时，钢轨映射位移峰值增长速率逐渐变缓。

3.3 剪切钢筋纵向刚度的影响

CA 砂浆层剪切钢筋初始刚度ksb取2 400 kN/mm，考虑剪切钢筋失效和剪切钢筋刚度缩放系数k′sb/ksb为0.05，0.1，1.0 和10 时，对桥梁纵向变形下钢轨纵向映射变形的影响，结果如图14～16所示。

从图14～16可知：剪切钢筋刚度变化对钢轨纵向映射变形影响显著。当剪切钢筋失效时，钢轨纵向映射变形峰值下降了23.61%，钢轨映射变形增加了28.03%。当k′sb/ksb取值小于0.1 时，剪切钢筋刚度对钢轨映射变形影响较小，Rc在4.40～4.60之间，UMRD在2.5～2.6 cm 之间。当k′sb/ksb取值大于0.1 时，剪切钢筋刚度增大对钢轨映射位移峰值和Rc有较大影响，此时，钢轨纵向映射变形对剪切钢筋刚度的变化有较强敏感性。

图14 剪切钢筋刚度对钢轨纵向映射变形的影响Fig.14 Influence of shear bars'stiffness on mapping rail deformation

图15 剪切钢筋刚度对钢轨映射变形峰值影响Fig.15 Influence of shear bars'stiffness on the maximum of mapping rail deformation

图16 剪切钢筋刚度对钢轨映射变形系数影响Fig.16 Influence of shear bars'stiffness on range of mapping rail deformation

3.4 CA砂浆层纵向刚度的影响

CA 砂浆层初始刚度ku-ca为90 kN/mm，考虑CA 砂浆层刚度缩放系数u-ca为0.01，0.1，1.0，10 和100 时，对桥梁纵向变形下钢轨纵向映射变形的影响，结果如图17～19所示。

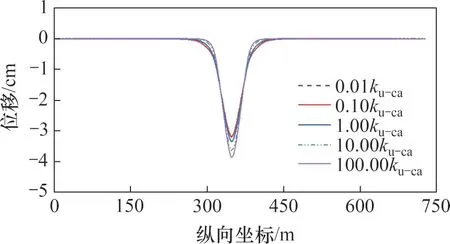
图17 CA砂浆层刚度对钢轨纵向映射变形的影响Fig.17 Influence of CA layer's stiffness on mapping rail deformation

图18 CA砂浆层刚度对钢轨映射变形峰值的影响Fig.18 Influence of CA layer's stiffness on the maximum of mapping rail deformation

从图17～19 可知：当/ku-ca小于0.1 时，钢轨纵向映射位移变化相对较小，钢轨映射位移峰值在3.2 cm 附近变化，Rc在3.93～3.97 之间。当/ku-ca为10 和100 时，钢轨映射位移峰值分别增加了8.9%和15.4%，Rc分别降低了14.5%和22.3%。随着CA 砂浆层刚度增大，钢轨映射变形逐渐增大，但是钢轨映射变形逐渐降低，即钢轨映射变形同桥梁变形的跟随性增强。与扣件刚度以及剪切钢筋刚度变化对钢轨映射变形的影响相比，CA砂浆层刚度对钢轨映射变形的影响较小。

图19 CA砂浆层刚度对钢轨映射变形系数的影响Fig.19 Influence of CA layer's stiffness on range of mapping rail deformation

3.5 滑动层纵向刚度的影响

滑动层层间初始刚度ku-h为12 kN/mm，考虑滑动层刚度缩放系数/ku-h为0.01，0.1，1.0，10和100时，对桥梁纵向变形下钢轨纵向映射变形的影响，结果如图20～22所示。

图20 滑动层刚度对钢轨纵向映射变形的影响Fig.20 Influence of sliding layer's stiffness on mapping rail deformation

从图20～22可知：钢轨纵向映射变形对滑动层刚度变化不敏感。当u-h从0.01 增加到100时，钢轨映射位移峰值仅在3.2～3.4 cm变化，Rc基本上保持在3.6附近，钢轨纵向映射变形所受影响很小。造成该现象的原因为：剪力齿槽为滑动层纵向主要传力构件，相比之下，滑动层刚度相对较小，/ku-h在0.01～100范围内变化，并不会对轨道-桥梁系统纵向层间传力机制造成较大影响，从而钢轨纵向映射变形变化不大。

3.6 剪力齿槽纵向刚度的影响

图21 滑动层刚度对钢轨映射变形峰值的影响Fig.21 Influence of sliding layer's stiffness on the maximum of mapping rail deformation

图22 滑动层刚度对钢轨映射变形系数的影响Fig.22 Influence of sliding layer's stiffness on range of mapping rail deformation

剪力齿槽初始刚度ks为1×106kN/mm，考虑剪力齿槽失效以及剪力齿槽刚度缩放系数k′s/ks为0.001，0.01，0.1 和1 时，对桥梁纵向变形下钢轨纵向映射变形的影响，结果如图23～25所示。

从图23 可知：当考虑剪力齿槽失效时，桥梁纵向变形引起的钢轨映射变形峰值仅为0.95 cm，而Rc高达10.8，同时，钢轨映射变形峰值的位置将移动至第四跨桥梁跨中。随着k′s/ks增大，剪力齿槽刚度变化对钢轨纵向映射变形的影响逐渐平稳。从图24和图25可知：与初始结构参数工况时的钢轨映射变形峰值和范围相比较，当k′s/ks取0.1时，UMRD仅下降了3.34%，Rc仅增长了4.45%，即当缩放系数大于0.1时，剪力齿槽刚度变化对钢轨映射变形的影响不大。同时，由于在4号桥墩固定支座上方布置有剪力齿槽，随着k′s/ks增大，钢轨映射变形峰值发生的位置逐渐从第四跨桥梁跨中向4号桥墩附近移动。