地面不平条件下考虑滑动转向特性的履带车辆路径跟踪控制

康翌婷，张煜，曾日芽

(1.北京科技大学机械工程学院，北京，100083；2.比亚迪汽车工业有限公司产品规划及汽车新技术研究院，广东深圳，518118)

履带式车辆因其较高的通过性能被广泛应用在复杂地形环境中执行任务[1-3]。路径跟踪控制是履带式车辆自主行驶的相关研究中的重要内容。但是在复杂环境下，实现履带式车辆的精确稳定的路径跟踪控制仍有许多问题需要解决。首先，履带式车辆是具有非完整约束的复杂非线性耦合系统，其在运动过程中还会不可避免地发生滑移滑转，这部分特性难以精确估计[4]。其次，在进行高精度路径跟踪时，还需要充分考虑系统的模型误差、控制精度等内部因素和地形环境等外部因素的影响[5-7]。因此，在充分考虑履带式车辆的滑动转向特性的前提下，开展地面不平条件下的路径跟踪控制方法研究具有重要的参考意义。

在履带车动力学建模方面，BEKKER[8-9]提出了履带与地面压力分布的理论性研究，并提出了一套半经验性的地面-车辆系统数学模型。韩庆珏等[10]通过模拟深海履带式采矿车行驶的海泥特性，分析了车辆在海底所受的各项阻力，并建立了履带式采矿车的动力学模型。李雨谭等[11]提出了一种地面力学通用数学模型，可获得履带的最小驱动力矩。李力等[12]基于多刚体理论，采用ADAMS/ATV 软件建立履带式车辆的三维动力学模型并对其越障性能进行仿真研究。上述对履带式车辆动力学特性的研究为建模过程提供了理论参考。然而，充分考虑履带与地面接触特性，尤其是在起伏不平的地面条件下的作用力模型仍然缺乏。

由于履带式车辆在运动过程中总是伴随着高速侧履带的滑转和低速侧履带的滑移，导致实际运动轨迹与理论模型结果存在较大偏差，因此国内外学者对履带车的滑动转向特性开展了很多研究。芮强等[13]开展了履带车辆转向性能参数分析与试验研究。熊光明等[7]通过迭代求解履带车的滑动参数，实现了未来一段时间内的运动轨迹预测。在滑移率的估计方面，李波[14]用里程计方法计算机器人的移动速度，用光电编码器获得轮子的转速信息，从而获取机器人移动时的滑移率。周波等[15]基于带有履带-地面滑动效应的履带机器人模型，利用非线性估计方法进行滑移率估计。在目前的滑移率估计方法研究中，虽然复杂的算法能够获取更高精度的结果，但同时也需要对大量数据进行实时运算，对硬件方面提出了更高的要求。因此，需要提出一种实时运算量较少，同时能保证精度的滑移率估计方法，用于对履带车辆滑动转向特性进行建模。

在履带式车辆的路径跟踪控制方面，运动过程中的打滑、地面条件变化和重心转移等因素会对履带车的运动控制造成干扰，因此需要提出一种能够抵抗扰动的控制方法。刘路等[16]基于降维变系数控制方法实现了履带机器人在三维崎岖路面的路径跟踪。胡家铭等[17]设计了基于模型预测控制的履带车辆轨迹跟踪控制器，系统处理了建模误差、环境约束以及执行机构约束。HONG等[18]提出了基于履带式海底采矿车运动学模型的路径跟踪算法，该算法考虑了履带的侧滑、车辆的纵向和横摆模型。尽管上述研究考虑了履带式车辆的滑动转向特性和环境约束，然而对于未知的起伏不平的复杂地面条件，需要提出一种具有较强自抗扰性的控制方法，以适应外界环境的变化。

本文作者根据履带式车辆的受力特点，建立了基于球-面接触原理的动力学模型；通过实车稳态转向实验采集了实际转向轨迹和履带车横摆角速度，提出了履带式车辆的滑移率估计方法，并结合履带车运动学特性进行了模型改进，设计了基于深度确定性策略梯度的控制算法，并通过在平整和不平地面条件下进行路径跟踪控制对算法的自适应性和自抗扰性进行验证。

1 基于球-面接触原理的履带式车辆动力学建模

基于球-面接触原理，建立履带式车辆的动力学模型。由于履带的质量占整车质量比例较小，因此，假设履带质量可被忽略，则履带相对地面运动时产生的摩擦力可视为0。简化后履带式车辆在地面运动时的受力如图1 所示。图1 中，v为履带车的前进速度；fn和ff分别为地面对各轮的法向力和切向力。

图1 基于球-面接触原理的履带式车辆受力分析Fig.1 Force analysis of a tracked vehicle based on spheresurface contact principle

地面作用于支撑轮、从动轮和驱动轮的法向力方向垂直于轮与地面的接触平面，将轮-地面接触等效为球-面接触，用于计算地面作用力的方向和大小。基于球-面接触原理，利用MapleSim 软件建立了履带式车辆动力学模型，如图2所示。履带车模型的可视化如图2(a)所示。履带部分的模型由机架、球面接触模块以及支撑轮、从动轮和驱动轮的可视化模块组成，如图2(b)所示。通过建立球-面接触模块(图2(c))获取地面接触信息并计算各轮受力情况。

图2 利用MapleSim建立的履带式车辆动力学模型Fig.2 Dynamic model of a tracked vehicle built in MapleSim

球-面接触模块的球心坐标以如下方式确定：如图2(d)所示，在履带车运动的大地坐标系XYZ中定义球心Qb的坐标为(xb,yb,zb)，以坐标系原点为起点，Qb为终点的向量为Qb。为了得到接触平面法向量，在Qb的地面投影坐标点Q′b附近，以较小的偏移距j定义3个点即Qb1，Qb2和Qb3，其坐标分别 为(xb,yb+ 2j,zb1)，(xb-j,yb-j,zb2) 和(xb+2j,yb- 2j,zb3)。其中，zb1，zb2，zb3是由Qb1，Qb2，Qb3在XY平面的投影位置，结合对应的环境模型中地面的高程信息所得。由这3点坐标可得接触平面的法向量P为

于是法向量在三轴上各分量的权值n为

坐标原点到3个坐标点中心的向量Pc为

在球-面接触模块中，将球等效为弹簧阻尼系统，用以计算法向力。球心与接触面的距离d为

距离d即为弹簧的形变量，因此，弹簧力fk为

式中：k和c分别为球-面接触模块等效弹簧阻尼系统的弹性系数和阻尼系数，可根据履带车的悬挂性能和履带材质确定；Rb为球模块的半径，与球模块所在位置的轮的半径相同。

球与接触面间的法向力fn为

定义球与地面间的附着系数为μ，可得切向力ff为

2 考虑滑动转向特性的履带车辆模型改进

2.1 履带式车辆转向运动学建模

履带式车辆在转向时总是伴随着履带相对于地面的打滑[19]，导致实际转向半径与理论模型计算的转向半径之间、实际横摆角速度与理论横摆角速度之间总是有一定的差距。履带式车辆的转向过程如图3 所示。其中，L为履带接地长度，B为两侧履带中心线间距，O为车辆质心，OT和OR分别为车辆理论转向中心和实际转向中心，RT和R分别为车辆理论转向半径和实际转向半径，wT和w分别为车辆理论横摆角速度和实际横摆角速度，v1和v2分别为低速侧和高速侧履带的卷绕速度(理论线速度)，vr1和vr2分别为低速侧和高速侧履带的牵连速度(实际线速度)。

从图3 可以看出，由于v1＜vr1，v2＞vr2，因此，实际转向半径大于理论转向半径。通常情况下难以获取两侧履带准确的牵连速度，但实际转向半径和实际横摆角速度可通过采集车辆轨迹和车身角速度的方式获取，因此，可通过采集实际转向半径和实际横摆角速度对转向时履带的滑移滑转程度进行估计。

图3 履带车辆转向过程示意图Fig.3 Steering process of tracked vehicle

两侧履带的卷绕速度表示为

式中：i=1，2，w1和w2分别为低速侧和高速侧履带驱动轮的输出转速；r为驱动轮半径。

由履带卷绕速度可以得到履带车辆的理论横摆角速度wT和理论转向半径RT[20]分别为：

低速侧和高速侧履带的滑移率δi(i=1，2)定义如下：

由履带牵连速度可计算实际横摆角速度w和实际转向半径R分别为：

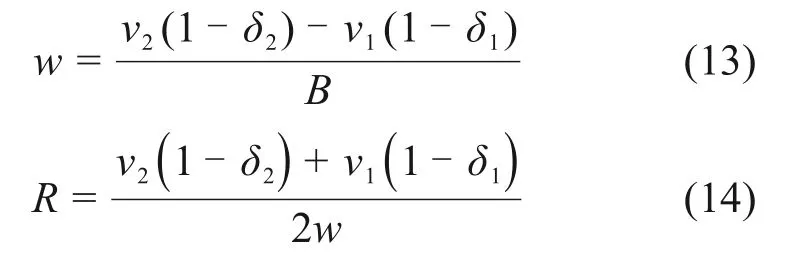
已知v1，v2，w，R时，可估计当前两侧履带的滑移率为

2.2 基于稳态转向实验的履带式车辆滑移率估计

为了获取履带式车辆的滑动转向特性，开展了稳态转向实验，实验在平坦的铺设地面进行。通过给定两侧履带驱动电机固定的转速差，使车辆进行稳态转向运动。实验所用的履带车参数如下：左右履带中心距B为0.67 m，驱动轮半径r为0.15 m，履带车质量为80 kg。由工控机向电机控制器发送转速命令，由车上搭载的差分GPS 系统获取车辆运动轨迹、横摆角速度等信息，记录在工控机中，搭建完成的履带车辆实验系统如图4(a)所示。按两侧驱动电机转速平均值将实验分为3组，分别为200，400 和600 r/min。每组包含8 个不同转向半径的实验，每次将一侧驱动电机转速从平均值增加10 r/min，另一侧减少10 r/min；当转速差达到100 r/min 时，高速侧电机转速每次增加50 r/min，低速侧每次减少50 r/min，直到两侧转速差达到400 r/min。交换两侧转速进行相同实验，得到车辆在左转和右转时的稳态转向特性。实验过程中电机转速分组如图4(b)所示，wH和wL分别为高速侧和低速侧的驱动电机转速。

图4 稳态转向实验方案Fig.4 Experimental scheme of steady-state turning

采用最小二乘法对实验所得的转向轨迹进行拟合，获得履带车实际转向半径数据，理论、实际转向半径和理论、实际横摆角速度的关系如图5所示。

由图5可知，实际半径R与理论半径RT、实际横摆角速度w与理论横摆角速度wT均呈线性关系，通过直线拟合的方式可得R=kRRT+bR，w=kwwT+bw。拟合直线的斜率、截距和判定系数R2如表1 所示，由判定系数和可知，回归直线对实验结果的拟合程度较高。

表1 拟合直线的斜率、截距和判定系数Table 1 Slope,intercept and R2of fitting curves

图5 理论模型与实验结果拟合直线Fig.5 Data fitting of theoretical and experimental results

利用履带车稳态转向实验数据结果，结合式(15)，可得滑移率计算方程为

2.3 模型改进

通过稳态转向实验获得履带车辆的滑动转向特性后，可实时估计两侧履带的滑移率，结合式(12)可获得两侧履带的牵连速度，将其输入至基于球-面接触原理建立的动力学模型(改进前)，形成考虑滑动转向特性的履带车辆动力学模型，改进后的模型结构如图6所示。

图6 考虑滑动转向特性的履带车辆改进模型Fig.6 Improved model of tracked vehicle taking account of skid-steer characteristics

模型的尺寸和质量参数与2.2节用于稳态转向实验的履带车的相同。在球-面接触模块中，为计算接触平面法向量定义的偏移距j取5 mm，等效弹簧阻尼系统的弹性系数k取1 kN/m，阻尼系数取c取1 N·s/m。对改进前和改进后的模型进行稳态转向仿真，采用和实车实验相同的高低速驱动电机转速输入(如图4(b)所示)，获取模型输出的轨迹和横摆角速度响应。驱动电机转速为200 r/min 时改进前后模型转向半径、横摆角速度与实际结果对比如图7所示，图中，转速差为履带高速侧和低速侧电机输入转速之差。

图7 驱动电机转速为200 r/min时改进前后模型和实车实验结果对比Fig.7 Comparisons of unimproved,improved models and experimental results at 200 r/min

从图7可知，在驱动电机转速200 r/min下，由于没有考虑履带车辆的滑动转向特性，改进前模型的转向半径要小于实车的转向半径，而理想的横摆角速度要大于实际值，尤其当转速差较大时，理想横摆角速度与实际值的差距就更加明显。当驱动电机平均转速分别为400 r/min和600 r/min时，其对比结果类似。当考虑了履带车转向过程中低速侧滑移、高速侧滑转的特性后，改进后模型所输出的轨迹半径和横摆角速度与实车实验数据基本保持一致，因此，将改进后的模型作为被控对象，开发基于深度强化学习的路径跟踪控制器具有更实际的参考意义。

3 基于深度确定性策略梯度的路径跟踪控制器

将地面不平度作为外界扰动，基于深度确定性策略梯度算法设计路径跟踪控制器，考虑跟踪误差、前进速度、控制器输出等多个控制目标，在平整地面的仿真环境中开展控制器的训练，利用深度确定性策略梯度算法的自抗扰性能，实现在不平地面上稳定和精确的路径跟踪控制。

3.1 深度确定性策略梯度算法

深度确定性策略梯度算法(deep deterministic policy gradient，DDPG)是结合了深度卷积网络和强化学习的算法，不仅能够接收高维输入，还能够解决连续动作空间问题。在DDPG 的训练过程中，会随机产生噪声对其输出的动作产生影响，因此，经过训练的DDPG 算法具备一定的自抗扰性能。DDPG算法的框架如图8所示[21-22]。

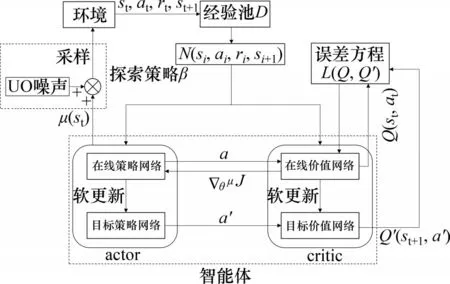
图8 DDPG算法框架结构Fig.8 Frame of DDPG algorithm

框架中智能体由策略网络和价值网络组成，策略和价值网络又分别由一个在线网络和一个目标网络组成，目标网络的结构和在线网络完全相同，以此来克服单个网络不稳定的问题[23-24]。在训练过程中，智能体需要尽可能探索到完整的动作空间，寻找潜在的更新策略，因此，引入随机噪声，将动作决策时的确定性过程变成随机过程，再从这个随机过程中采样得到动作的值。将Uhlenbeck-Ornstein(UO)随机过程作为被引入的随机噪声，探索得到这个动作策略并不是最终所需要的策略，仅被用于训练过程。

通过Actor与环境之间探索过程的交互，产生学习样本并存储到经验池中。在更新阶段，从经验池中获取小批量训练样本数据，先将其中下一步的状态量si+1放入目标策略网络得到目标动作a′，然后将si+1和a′共同作为目标价值网络的输入并获得目标价值Q′。得到目标回报值之后，再将si，ai共同作为在线价值网络的输入，计算得到实际价值Q，经由最小化误差L(Q,Q′)更新在线价值网络，再由在线价值网络计算在线策略网络的梯度∇θμJ来确定其更新方向。

3.2 状态、动作与奖励设计

路径跟踪控制器所需要的车辆状态信息中，最重要的因素就是车辆当前位置坐标与参考路径的目标位置坐标之间的误差。在跟踪的过程中，车辆航向角与目标航向角之间的误差能够指示车辆修正行进方向。在跟踪的过程中还应保证能实现目标速度，减小实际速度与目标速度之间的误差。上述误差定义如图9所示。图中：XOY为大地坐标系，XbObYb为固定在车体上的坐标系；(xc,yc)为质心O点在大地坐标系的位置；θ和v分别为实际航向角和实际前进速度；(xref,yref)为目标路径上当前的目标位置C′坐标；θref和vref分别为目标航向角和目标前进速度。

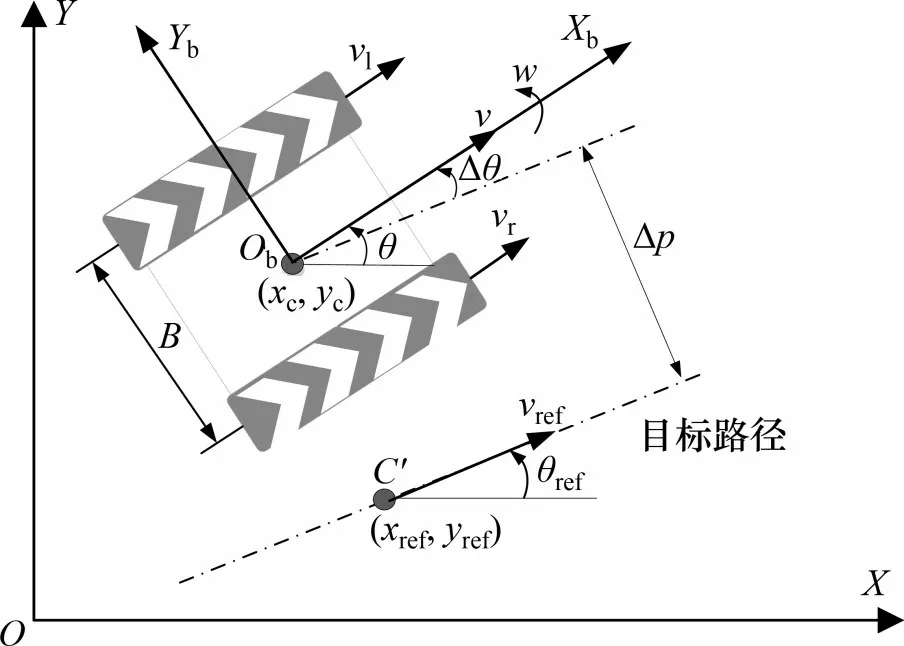
图9 履带车辆路径跟踪误差定义Fig.9 Definition of path tracking errors for a tracked vehicle

各项误差计算如下：

式中：Δp为位置误差；Δθ为航向角误差；Δv为质心速度误差；λ为位置误差方向系数，当目标路径位于车辆左侧时，取λ= 1，当目标路径位于车辆右侧时，取λ= -1。

为了提高智能体对位置、航向角和速度的调节能力，将上述3个误差及其一阶微分作为DDPG算法的状态EState：

将左右两侧履带的卷绕速度(理论线速度)变化量作为控制器输出，由此定义算法中动作VAction：

路径跟踪的目标是令车辆的实际运动轨迹与目标路径之间的误差最小，因此将位置误差作为首要控制目标，航向角误差作为次要目标，同时考虑跟踪速度误差和控制输出的变化。综合以上目标，本文设计履带车辆路径跟踪控制的四级奖励：1级：位置误差；2级：航向角误差；3级：质心前进速度误差；4 级：履带卷绕速度的变化量。根据奖励等级分配权重，位置误差、航向角误差、质心前进速度误差的权重系数分别为-0.03，-0.02，-0.01。当上述的各项误差越小，则奖励越高。履带卷绕速度的变化量这一目标具有稳定输出的作用，履带卷绕速度的变化量越小，奖励越高，但如果过度约束会影响控制效果，故其权重系数为-0.001。四级奖励函数设计中以各项误差和控制器输出的二次函数反映各项奖励的变化率。另外，总体奖励函数设计中考虑了对仿真提前终止的惩罚，当位置误差和航向角误差控制在较小范围内的额外奖励，以及对履带车有效行驶路径长度的奖励。总体奖励函数如下：

式中：fdone为仿真提前终止惩罚项，当仿真提前终止时，fdone为1，反之为0；fp为位置误差额外奖励项，当整段仿真内| Δp|的最大值小于0.01 m时，fp为1，反之为0；fh为航向角误差额外奖励项，当整段仿真内| |Δθ的最大值小于0.1 rad 时，fh为1，反之为0；s为履带车质心轨迹在XY平面投影的长度。

4 仿真验证

以改进后的履带式车辆动力学模型为被控对象，在仿真环境开展平整地面上典型路径的跟踪控制训练。改进后的模型考虑了实车的滑动转向特性，结果与实车实验数据更为接近，用于强化学习训练更具有实际意义。

4.1 控制器训练

为验证本文所提出的基于DDPG 算法的路径跟踪控制器的有效性和自抗扰性，先令控制器在平整地面条件下进行典型路径的跟踪训练，再将其应用于不平地面并对相应的目标路径进行跟踪控制。平整地面上以正弦曲线y= sin(0.7x)作为目标路径进行训练，考察控制器对于变曲率目标路径的跟踪能力。目标前进速度vref设为1 m/s，训练的目标奖励值为10 000，实际达到的奖励值为10 622.69，训练次数为2 164 次，训练结束时的平均奖励值为4 853.11，训练总时长为15 344 s。

训练后的控制器在不平地面上跟踪目标路径，测试其自抗扰性。根据国标GB/T 7031—2005[25]中C 级地面不平度标准，在MapleSim 仿真环境中设计了一个边长为60 m 的正方形不平地面模型，此模型的Z方向长度变化范围在±0.03 m 之间，如图10所示。履带车的动力学模型中的球-面接触模块可通过查表函数获取接触位置相应的高程信息，并用以计算法向力和切向力。

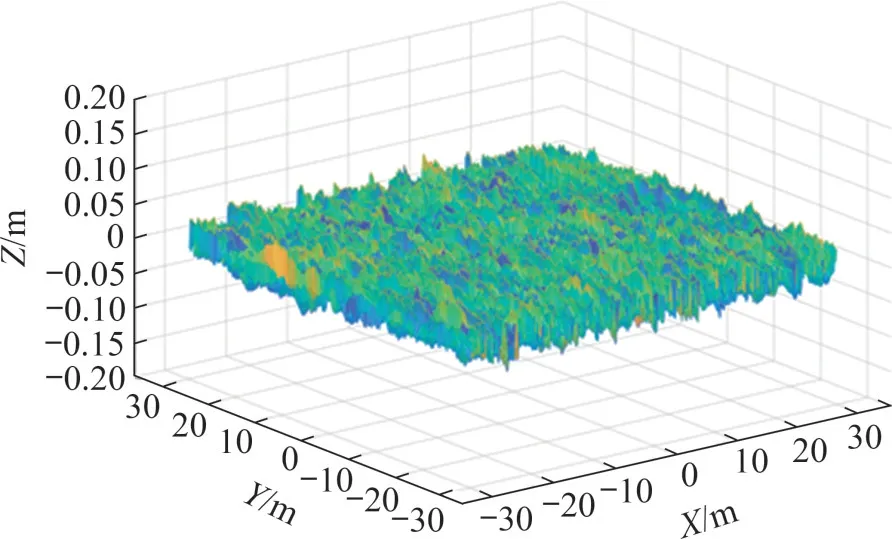
图10 MapleSim仿真环境中的不平地面模型Fig.10 Uneven terrain in MapleSim simulation environment

4.2 仿真结果

本文所提出的基于DDPG 算法的路径跟踪控制器在平整地面和不平地面下的跟踪效果如图11所示。可见：在实际奖励值为10 622.69 的训练结果下，平整地面上跟踪的位置误差绝对值小于0.02 m，航向角误差绝对值小于0.05 rad，跟踪速度在一段时间后逐渐趋近于参考速度1 m/s，左右履带的卷绕速度在稳定后变化较为平稳。将该控制器应用于不平地面上跟踪目标路径时，位置误差绝对值小于0.06 m，绝对航向角误差小于0.25 rad，跟踪速度和控制量的振荡较平整地面要更为明显，其质心的Z向位移变化如图11(e)所示。从图11(e)可以看出：在不平地面的影响下，车辆质心的垂向位置也产生相应的起伏。从以上路径跟踪效果对比可以看出，在平整地面工况下训练的控制器在不平地面上仍然能够对相应的目标路径进行跟踪，尽管控制效果相较于平整地面时有所降低，但其在不平地面上无须调整参数或重新训练，控制器的可行性和自抗扰性得到验证。

图11 经过训练后的正弦曲线路径跟踪结果Fig.11 Results of tracking a sinusoid path after training

5 结论

1)基于球-面接触原理，提出了履带式车辆动力学建模方法。基于稳态转向实验数据提出了履带式车辆的滑移率估计方法，综合基于球-面接触原理建立的动力学模型提出了反映履带车辆滑动转向特性的改进模型。经验证，在相同的输入转速下，改进模型的转向半径和横摆角速度响应与实验数据更为吻合，作为被控对象用于强化学习训练更具有实际的参考意义。

2)基于深度确定性策略梯度方法，将路径跟踪的位置误差、航向角误差和跟踪速度误差及三者的变化率作为强化学习中的状态，并利用四级奖励函数，设计了路径跟踪控制器。在平整地面上开展控制器的训练，并应用于不平地面条件下跟踪相应的目标路径。仿真结果证明，无需整定参数或重新训练，在平整地面工况下训练的控制器在不平地面上仍然能够对相应的目标路径进行跟踪，控制器的可行性和自抗扰性得到验证。