适时适当地干预 潜移默化地成长

周承仕

[摘  要] 對于解题能力的提升，不同教师有着不同的见解，部分教师认为“刷题”是最直接、最高效的方法，然过多“刷题”不仅容易使学生出现思维定式，而且容易产生消极情绪，这并非最佳方案. 文章指出，解题过程的分析、通性通法的提炼及知识体系的建构才是提升解题能力的捷径，教师应充分发挥其引导作用，通过干预和指导来锻炼学生的思维，提升学生的学习能力.

[关键词] 解题能力;干预;学习能力

教师是学习的领路人，学生的学习能力和思维能力的提升离不开教师悉心指导，教学中教师适度和适当的干预不仅可以让学生少走弯路，而且可以让学生“真懂真会”，从而提升学习效率. 笔者经过不断地实践研究，获得了一点成效，分享给同行供参考.

借过程分析，让思维更严谨

在解题中常出现答案正确、然过程错误的现象，有部分原因是学生的书写过程不够规范，于是造成了错误;然大多数错误还是因为学生的思维不够严谨造成的，如在解题时添加或减少了条件，从而出现了“对而不会”的现象. 因此，教学中要杜绝“重结果缺过程”的现象，只有通过对过程的分析和思考才能暴露学生的思维误区，从而对症下药，正确求解.

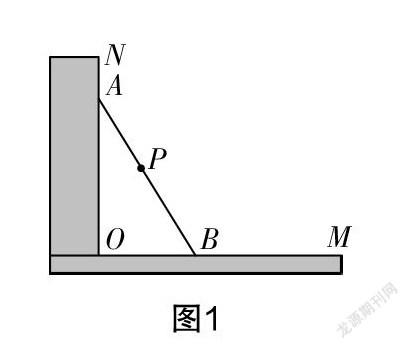
案例1  如图1所示，已知有一条长2.5米的木棍AB斜靠在墙上，地面OM与墙ON垂直. 此时OB的长度为0.7米，AB的中点为P.

（1）若木棍沿墙面逐渐下滑，当顶点A下滑0.4米时，试求点B向右滑动了多少米.

（2）在木棍AB下滑的过程中，中点P到点O的距离是否发生了变化？请说明理由.

（3）木棍AB下滑到什么位置时，可以使△AOB的面积最大？此时的值是多少？

解题分析  第（1）问主要考查的是勾股定理的应用. 根据题目条件很容易得出OA为2.4米，当顶点A下滑0.4米时可得OA为2米，斜边AB不变. 根据勾股定理可以求出点B向右滑行后到点O的距离为1.5米，故可得点B向右滑行了0.8米. 第（2）问看似为复杂的动点问题，然仔细分析后可知其为直角三角形斜边中线定理，因为斜边AB不变，所以斜边上的中线OP也不变. 前面两个问题大多数学生都能解决，并且可以思路清晰地正确求解. 第（3）问是一道考查学生综合能力的题目，有一定难度，然从结果来看，大多数学生都得出了正确答案. 为了更好地呈现学生的思维过程，笔者让学生通过口述的形式讲述其求解过程.

生1：我认为当OP⊥AB时，△AOB的面积最大，所以我是根据这个思路求解的.

师：你的理由是什么呢？

生1：这个我不太能说得清楚，凭借经验，这类题目的答案一般都是在特殊的位置，所以我认为当OP⊥AB时就是那个特殊的位置.

师：虽然你的答案是正确的，但缺少对过程的正确理解，有没有同学可以帮助他呢？

生2：我们知道对于周长相等的四边形，正方形的面积大于长方形的面积，按照这个思路可知，当OA=OB时，△AOB的面积最大. 而当OA=OB时，正好是OP⊥AB. （很多学生认为生2说得很有道理，纷纷点头）

师：是这样吗？（教师表示疑惑，这时反应快的学生已经发现了问题）

生3：生2的说法有问题，因为只有周长不变的情况下上面的说法才能成立，而从第（1）问可知OA缩短了0.4米，而OB增加了0.8米，显然其周长变化了. 另外，可以设OA=a，OB=b，可得a2+b2=6.25，从这个等式也可以看出OA+OB是不确定的.

师：分析得很有道理. 如何将a2+b2=6.25变形，使其转化为类似ab这种与三角形面积相关的式子呢？（教师话音刚落，学生就开始抢答了）

生4：（a+b）2-2ab=6.25.

生5：（a-b）2+2ab=6.25.

师：很好，现在结合生2的思路，可以得到什么呢？

生6：当ab的值最大时，△OAB的面积最大. 由（a-b）2+2ab=6.25可知，当ab的值最大时，（a-b）2的值最小，此时a=b，△OAB为等腰直角三角形，OP⊥AB，S=×2.5×1.25=1.5625.

通过师生和生生的互动交流，不仅理清了问题的来龙去脉，而且挖掘出了问题的本质，使学生不仅“懂”而且“会”. 数学是一门严谨的学科，虽然有时也应用了猜想和假设，然并非凭空猜想，其需要符合客观的事实. 在第（3）问的求解过程中，虽然生1和生2的答案是正确的，然其求解过程不够充分，故出现了“对而不会”的现象. 因此，在教学中教师不能仅关注结果，更应关注解题过程，只有经历了过程才能知道学生是否真的“既懂又会”，从而培养他们严谨的数学思维.

借多种解题，提炼通性通法

众所周知，数学习题千变万化，不可能做完. 提升解题能力单凭机械盲目的强化训练往往收获甚微，而且机械训练会占用学生大量的思考和总结归纳的时间，致使学生因缺乏思考而解题思路单一僵化，因缺乏总结归纳而无法提炼解题的通性通法，不利于思维的发展. 没有好的思维习惯和好的解题策略，解题能力难以提升，因此教学中教师要适时引导，让学生重视通用法和基础法的提炼，从而让学生既可夯实基础又能提升应变能力.

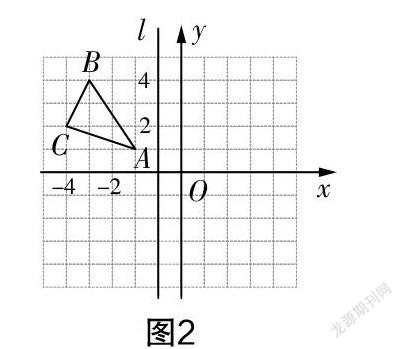
案例2  △ABC的位置如图2所示，直线l经过点（0，1）且与y轴平行，△ABC与△ABC关于直线l对称.

（1）画出△ABC，并写出其对应点的坐标;

（2）若点P在△ABC内，坐标为（a，b），写出△ABC中与点P对应的点P的坐标.

解题分析  第（1）问是基础类问题，相对容易，学生很容易得出答案. 第（2）问的难度略有提高，其主要考查学生的观察能力、动手能力，以及转化和类比等数学思想. 大多数学生根据观察第（1）问中各对应点坐标的关系猜想P的坐标，进而得出答案;也有少数学生使用了平移方法，然有些学生对于平移方法表示不理解，于是教师让采用平移方法的学生进行了讲解.

生7：将直线l与△ABC考虑为一个整体，将直线l向右平移一个单位，使直线l与y轴重合，此时点P的坐标为（a+1，b），则其关于y轴对称的点的坐标为（-a-1，b），这时再将（-a-1，b）向左平移一个单位，即得P的坐标为（-a-2，b）.

通过生1的讲解，大部分学生表示理解了，并且会用平移法求解对应点的坐标. 在教学中要鼓励学生进行多角度的观察和思考，通过类比、猜想、归纳等活动来发现问题的本质特征，从而发现解题的一般方法. 为了让学生的思维再“跳一跳”，教师继续追问：你们认为哪种方法更好呢？

在追问的引领下，学生除了关注结果是否正确外，开始寻找最优的解决策略. 然针对部分学生仍对平移方法存在疑问，教师引导学生通过动手操作来真实演绎推理的过程. 首先教师让学生在纸上绘画△ABC并将其裁剪下来，接下来将△ABC向右进行平移，将y轴想象成直线l，这时写出平移后点P的坐标，最后让学生将△ABC向左平移至原来的位置，再写下此时点P的坐标. 通过动手操作，学生更加直观地了解了对称与平移. 为了让学生加深理解，教师还可以引导学生进行变式训练，如将“直线l经过点（0，1）且与y轴平行”改为“直线l经过点（0，-1）且与x轴平行”. 通过动手操作及变式训练的引导，不仅可以发散学生的思维，而且有助于学生从特殊规律发现一般规律，找到解决问题的通性通法，提升学生分析和解决问题的能力.

借变式训练，促知识迁移

数学知识点链接起来犹如一个大型“蜘蛛网”，它们相互关联、相互依存，然很多学生在知识构建时因忽略知识点之间的联系，致使漏洞出现. 究其原因，很大程度上与教师的教学方法有关：部分教师在教学时依然习惯用“题海战术”进行强化训练，忽视了例习题的示范性和典型性，忽略了对例习题的挖掘，学生无法领会例习题的真正意图，无法找到知识点之间的联系，从而限制了知识的迁移和运用. 为了改变这一现象，教师要重视例习题的拓展和引申，潜移默化地让学生从一个知识点“嫁接”至另一个知识点，从一个知识体系“跨越”至另一个知识体系，从而实现知识的全面系统构建，提升解题能力.

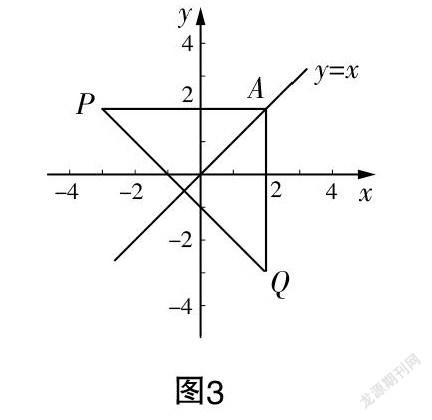
案例3  已知点P（-3，2）关于y=x对称，求其对称点的坐标.

解题分析  本题未给出图形，需要学生自己进行构造. 为了寻找点P的对称点，学生可以构造等腰直角三角形，如图3所示. 图形构造完成后很容易得出点A的坐标为（2，2），由点A的坐标可以推导出点Q（点P关于y=x的对称点）的坐标为（2，-3）.

显然通过数形结合使本题的求解过程更加清晰明了，为了检验学生的学习成果并让思维实现质的飞跃，教师设计了两个分层的变式题目：（1）写出点P（-3，2）关于y=-x对称的点的坐标;（2）写出点P（-3，2）关于y=x+2对稱的点的坐标. 变式题（1）依然是轴对称问题，其解题思路和解题方法与原题相同. 变式题（2）在轴对称的基础上增加了平移，潜移默化地实现知识的迁移，使学生的思维得到了升华. 在数学学习中，各知识点之间存在着千丝万缕的联系，因此要学好数学必须会转化，将不熟悉的、不够直观的问题根据已有知识进行迁移和转化，从而提升数学的综合应用能力.

总之，教学中要善于借助于思维过程暴露出的问题，通过适当干预，让学生“真懂真会”，提升学生的学习能力.