培养逆向思维,探寻解题新途径
2022-03-28段振富徐杰
段振富 徐杰




[摘 要] 数学思维是数学教学最终指向,在实际教学中教师对学生思维培养应该分为两个方向:既要重视正向思维发展,也要关注逆向思维培养.文章以一道中考试题为例谈谈如何利用逆向思维在解题过程中另辟蹊径、出奇制胜,然后结合对教材中求根公式的推导,阐述教学过程中如何培养学生的逆向思维.
[关键词] 数学教学;逆向思维;解决问题;中考数学
数学思维方式与思维习惯对解题的正确率与解题过程步骤的优化程度影响很大,鉴于数学知识内在的逻辑性,因此提升数学思维的发散性与逻辑性成了老生常谈的话题. 按照思维方向的不同分为正向思维与逆向思维,常规的思维是正向的,其顺应知识的形成方向,呈现为大众认知的普遍性;而逆向思维属于创造性思维的范畴,是在常规思考问题的方式上反过来寻找问题解决办法的方式,又被称为求异思维. 逆向思维是从正向思考方向的对立面或者其他路径入手,通过逆向或者转化的方式,找到解决问题的新途径[1].
从哲学角度来看,“逆”与“正”是对立统一的,彼此相辅相成,逆向思维能够在一定程度上对正向思维起到完整性的弥补,能够改善正向思维中思维定式的局限性. 在正向思维的基础上发展逆向思维,能够让学生学会从不同方位、不同角度、不同层次思考问题,增加思维的发散性,促进学生对知识的全面理解、牢固掌握、熟练运用,从而提升学生的思维全面性与创造性.
从心理学的角度来看,培养学生的逆向思维,在一定程度上可以调整学生的心理状态、优化学生的思维模式、拓展学生的思维路径,实现对学生心理过程的方向重建.不管是从学生解题能力提升、心理过程完善、哲学观念形成的角度来看,还是从学生个体观念成型、创新意识形成、考试适应性提升的角度来看,都应该在日常教学中重视培养学生的逆向思维能力.
下面,我们以2020年福建省中考数学卷第25题为例作说明.
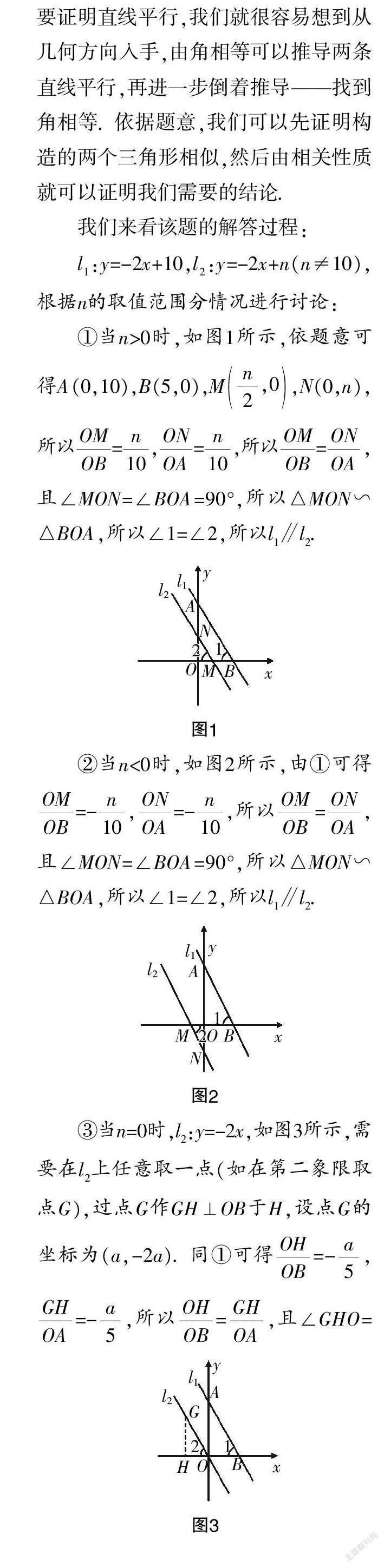
已知直线l:y=-2x+10交y轴于点A,交x轴于点B,二次函数的图像过A,B两点,交x轴于另一点C,BC=4,且对于该二次函数图像上的任意两点P(x,y),P(x,y),当x>x≥5时,总有y>y.
(1)求二次函数的表达式;
(2)若直线l∶y=-mx+n(n≠10),求证:当m=2时,l∥l;
(3)略.
对于第(2)问,按常规思路,考生多数采用正向思维解答:因为直线l1与直线l2的斜率相等,所以这两条直线就是平行的.这也符合教师日常的教学要求. 但对于本题,命题者意在考查“为什么斜率相等就是平行的”,所以考生直接“用结论去证明这个问题的答案”显然是不对的. 那么,考生到底该如何去思考这道题呢?从结论入手,倒过来思考!目标是要证明直线平行,我们就很容易想到从几何方向入手,由角相等可以推导两条直线平行,再进一步倒着推导——找到角相等. 依据题意,我们可以先证明构造的两个三角形相似,然后由相关性质就可以证明我们需要的结论.
由于要根据n的取值范围进行分类讨论,有一定难度,所以很多考生丢分严重. 当然,本题也可以利用三角函数(tanα)来解决,计算过程比上面应用相似三角形的办法简洁,在此不再赘述.
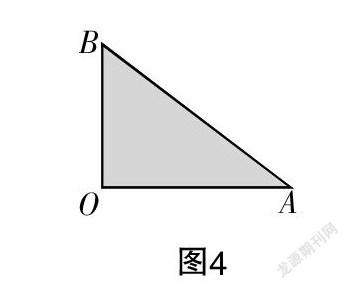
除了上面通过角度的关系来证明两条直线平行,考生亦可构造平行四边形来证明两条直线平行.以下,我们简叙思维过程:
考生由k=k直接得出l∥l时没有完整地进行分类讨论,或表示边长时没有使用绝对值(代数解法表述不规范),或忽略了条件“n≠10”. 根源在于思维不严谨,分类意识不够,逻辑能力不强,逆向思维能力没有得到培养和发展.这提醒我们,在日常教学中需要让学生形成变通思维,即当正向思维受阻时迅速转向逆向思维.
对学生逆向思维的培养不是仅通过一节专题课就可以实现的,而是需要教师在备课时通过先入为主的预设对学生进行逆向思维的培养,不断把逆向思维融入具体的教学过程中,比如常见的定义(概念)、定理、公式的学习过程中,通过长期的积累和摸索发现能够渗透逆向思维的地方. 具体而言,笔者总结了以下几方面常见的逆向思维渗透的模型.
首先,在数学概念教学过程中,教师要总结归纳某些概念的双向性,幫助学生在概念的理解上有全面的认识.例如,在“绝对值”的概念学习时,教师既要从正向提问“3的绝对值是多少”,也要从逆向提问“什么数的绝对值是3”. 在这样的双向思考下,学生才能对有理数的绝对值形成完整的理解.
其次,在数学定理的教学过程中,也要适当有意识地对学生的逆向思维进行针对性训练. 例如,在学习了几何图形的性质定理后,教师可以引导学生思考将性质定理的题设和结论颠倒过来,探究能否得到这个图形的判定定理.养成这样的逆向思考的习惯后,学生自然能在面对一个新的图形时,有意识、有方法地进行自主探究,在这个过程中学生的学习能力自然能够得到提升.
再者,在数学公式的教学中,教师也可以有意识地进行公式的逆向观察,培养学生获取信息的能力. 例如,在“加权平均数”的教学中,为了决定录取哪位应试者,教师通常会给出应试者各项考核项目的成绩,要求学生计算成绩的加权平均数,决定录取结果.反过来,教师也可以给出应试者成绩的加权平均数的计算过程,让学生分析考官对哪些考核项目更加重视,应试者在哪些考核项目上体现出了优势或劣势,应试者应该注意培养哪方面的能力才能有更大的机会被录取. 这样的逆向观察有助于学生加深对公式结构特点的认识,为创造性地利用数学公式解决问题打下基础.
笔者结合一元二次方程求根公式的教学,展示如何结合公式的推导过程进行逆向思维的培养. 在教授公式法解一元二次方程时,通过对一元二次方程的一般形式ax2+bx+c=0(a≠0)进行配方,得到
x+2=. 根据平方的非负性,进行分类讨论:①当Δ=b2-4ac>0时,推导出一元二次方程的求根公式x=,x=;②当Δ=b2-4ac=0时,x=x=-;③当Δ=b2-4ac<0时,方程无实数根. 进一步,在①②两种情况下,推导出根与系数的关系:x+x=-,xx=.至此,学生就可以开始使用求根公式解一元二次方程了.
又如,教材最后根据求根公式,能够推导出具有特殊结构的结果,即根与系数的关系:“两根之和”与“两根之积”. 诚然,这个结果在形式上非常简单,便于记忆. 那么我们能否进一步引导学生根据两根的结构特征,推导出两根其他的运算形式与系数的关系呢?比如x-x,(x≠0),x+x,x-x等.
通过上述的例子,我们可以发现,教师在教学中要善于研究和利用公式的代数结构,才能充分发掘公式的内涵,在学习新公式的同时对以往所学知识适当进行联系,实现触类旁通的目的,在推导过程中也能培养学生数学运算的核心素养. 在不同的思维路径下,学生还能更加深入地思考在推导求根公式的过程中为什么要分类讨论,根的判别式的作用在哪里,相比推导出公式后就急于通过大量的解方程的练习巩固公式的应用,这样的逆向思维对于学生建立完备的数学知识体系显然是大有裨益的.
总体来说,不管从学生解题能力提升、心理成长的角度来看,还是从学生哲学观念养成、创新意识发展的角度来看,培养学生的逆向思维都是初中数学教师的应有之举. 结合近几年在这个领域的尝试和摸索,笔者总结出了一些培养学生逆向思维的经验,在此与同行分享:
(1)从思维结构上来说,逆向思维与正向思维是对立统一的,是相辅相成、紧密相关的一个整体. 在我们日常教学过程中有很多环节都蕴含着渗透逆向思维的意识,比如因式分解与整式乘法的关系本身就是互逆的,以及勾股定理和勾股定理的逆定理亦是如此,许多几何的性质定理和判定定理同样互为逆命题,如角平分线、线段垂直平分线、平行四边形等. 在这些内容的教学过程中我们都应该抓住时机,培养学生的逆向思维.
(2)逆向思维是在应用的过程中培养起来的. 数学中有很多的运算形式是互逆的,如乘方与開方、乘法与除法、加法与减法. 它们之间彼此依存,又可相互转化,共同反映某种变化中的数量关系. 在同一级运算中,又可以相互转化[2],如减法法则可以转化为加法法则. 很多法则在应用的过程中也是采用逆用的方式来解决问题的,如同底数幂乘法法则、幂的乘方法则,有很多题目都需要公式逆用的思路来解决问题[3].
(3)逆向思维在初中数学学习中最常见的运用是反证法. 反证法从待证命题结论的反面入手,即假定结论的反面是正确的,然后结合已知条件,经过逻辑推理引出一个新的结论. 而这个新结论或与题设相矛盾或与已学过的定理、公理相矛盾,从而得出原命题结论的反面不正确,所以原结论正确. 当题目有“至少”“至多”等字样或以否定形式出现时,一般采用的就是反证法. 最近几年全国各地中考试卷中反证法出现的频率有增加的趋势.
总之,逆向思维的培养不能靠短时间的突击训练而完成,如果教学中教师有逆向思维培养预设的意识,经过一段时间的训练,让学生在潜移默化中形成双向思维模式构建的心理能力,这对提升学生的创新思维能力以及提供新的解题途径有很大的帮助.
参考文献:
[1] 彭石山. 逆向思维在解题中的应用[J]. 中学数学教学参考,2021(24):33-36.
[2] 沈晓生. 引导初中数学深度学习的逆向思维能力培养策略[J]. 中学数学,2021(16):36-37+49.
[3] 李福兴. 探讨逆向思维及其在数学分析中的应用[J]. 贺州学院学报,2008(03):118-121.
