阵面机械轴误差对相控阵雷达测角精度影响分析与验证*

唐晓雷,王索建

(南京电子技术研究所，南京 210039)

0 引 言

近年来随着作战环境和作战对象的多元化和复杂化，武器对抗体系对相控阵雷达的要求越来越高，相控阵雷达规模越来越大，复杂度越来越高，精度要求越来越苛刻。文献[1-2]研究了形变及安装引起的单元误差对相控阵雷达天线阵面电性能的影响，文献[3]对大型固定式相控阵雷达天线安装方式进行了研究,这些研究有力保证和推动了高精度相控阵雷达的实现。然而，作为相控阵雷达天线阵面重要安装参数的机械轴误差对相控阵雷达测角精度的影响却少有研究。张赟霞等人[4]在对地基相控阵雷达天线指向系统性误差分析中，定性分析了在仰角固定模式下倾角和不水平度误差对相控阵雷达方位和俯仰测角误差的影响，但对影响因素和影响模式未做深入研究。陶军等人[5]定性研究了机械轴误差在方位扫描角维度上对相控阵雷达测角的影响，并提炼出相控阵雷达测角误差与机械轴误差和扫描角之间的简约关系式，但未对其他影响因素与测角误差的关系开展分析。

机械轴作为相控阵雷达天线阵面设计计算电轴法向，是计算波控码的基础，包括阵面倾角T、阵面法向在水平面内投影与正北之间夹角Nt以及阵面不水平度Q。机械轴一般利用全站仪或者双水平仪等仪器仪表测量获取[6-7]，机械轴安装参考平面、仪器仪表、标校数据录取和过程传递、天线阵面长期使用后的基座结构形变等因素影响，导致机械轴产生误差。由于机械轴误差标校工作比较复杂，一般结合装备中修或大修工程开展，而机械轴误差对相控阵雷达测角精度受多维因素(T及误差、Nt及误差、Q及误差、方位和仰角扫描角)的共同调制,不同组合的影响模式和量级不同，规律不好掌握，虽然很多学者对相控阵雷达标校方法开展了研究[8-9],但均未能剥离出测角影响因素，更没有针对性的机械轴误差复核验证方法。

本文通过研究分析机械轴误差对相控阵雷达测角影响模式，在文献[5]的基础上，全面分析了各影响因素对相控阵雷达测角误差的影响，修正了实际情况下相控阵雷达波束指向公式。根据机械轴误差在方位法向上对相控阵雷达测角误差影响的特性,解算出机械轴误差与方位和俯仰测角误差之间的关系，提出一种机械轴误差验证方法。根据本文所提方法，结合相控阵雷达常规精度标校方法，通过简单的解算，即可验证相控阵雷达是否存在机械轴误差及误差量值，保障了相控阵雷达在寿命周期内的高精度。

1 相控阵雷达天线阵面机械轴误差模型

假设平面相控阵雷达天线阵面安装在阵面直角坐标系x″y″z″中的x″o″y″平面内，天线阵面机械轴相关参数为Nt、T、Q，机械轴误差分别为Δγ、Δδ、Δσ，阵面直角坐标系x″y″z″由空间直角坐标系XYZ经过旋转变换所得，所有旋转角逆时针旋转为正。阵面直角坐标系x″y″z″与空间直角坐标系XYZ对应关系如图1所示，其中，Δγ为Nt误差，Δδ为T误差，Δσ为Q误差；A为相对于阵面方位法向Nt的方位扫描角,E为仰角扫描角,R为目标点P相对于雷达坐标原点的距离。

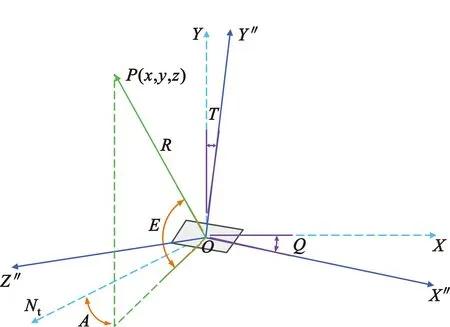
图1 空间直角坐标系到阵面直角坐标系的变换关系示意图

机械轴无误差时，空间直角坐标系到阵面坐标系的变换矩阵为L1，则有

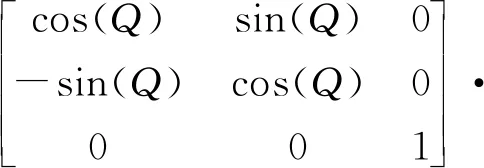
(1)

机械轴存在误差时，空间直角坐标系到阵面坐标系的变换矩阵为L2，则有

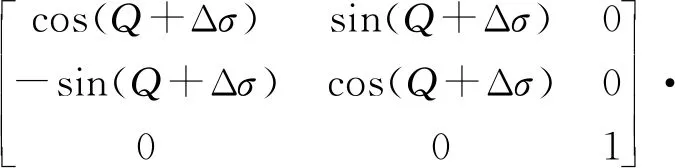
(2)

2 阵面机械轴误差对相控阵雷达测角精度影响分析

2.1 波束指向修正

理想条件下，相控阵雷达天线阵面机械轴相关参数为Nt和T,不存在不水平度Q，而天线阵面在实际安装过程中，天线安装基座由于各种原因，导致存在不水平度Q。根据经典理论公式，在图1所示的阵面坐标系中，理想条件下的方向余弦为

(3)

理想条件下，二维相控阵雷达天线阵面阵内相位差为

(4)

由公式(1)和公式(3)可得，实际条件下无机械轴误差时的方向余弦为

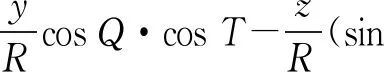
(5)

同理可得，实际条件下存在机械轴误差时的方向余弦为

sin(Q+Δσ)·sin(T+Δδ)·sin(Nt+Δγ))+

sin(Q+Δσ)·sin(T+Δδ)·cos(Nt+Δγ))，

cos(Q+Δσ)·sin(T+Δδ)·sin(Nt+Δγ))+

cos(Q+Δσ)·sin(T+Δδ)·cos(Nt+Δγ))。

(6)

由公式(4)～(6)可得，实际条件下的二维相控阵雷达天线阵面阵面相位差为

(7)

(8)

公式(7)和(8)分别为实际条件下，不存在和存在机械轴误差情况下计算相控阵雷达天线阵面波束指向时，阵内相位差的修正表达式。

2.2 机械轴误差对相控阵雷达测角精度影响分析

设定空间直角坐标系中空中目标点P(x,y,z)，相对雷达的方向分别为A、E，该坐标点在阵面直角坐标系中对应的点为P0(x0,y0,z0)，根据图1所示的空间直角坐标系与阵面直角坐标系旋转变换关系可得

(9)

根据图1所示目标空间几何关系可得

(10)

假设P0(x0,y0,z0)在没有机械轴误差的空间直角坐标系中对应的坐标点为P1(x1,y1,z1)，空间直角坐标系中对应的方位和俯仰角分别为A1和E1;在有机械轴误差的空间直角坐标系中对应的坐标点为P2(x2,y2,z2),空间直角坐标系中对应的方位和仰角分别为A2和E2。由公式(9)和(10)可得

即

(11)

由于阵面安装误差Δ一般都很小，远远小于1°，可得cos(Δ)≈1,sin(Δ)≈tg(Δ)≈Δ。后续分别讨论三种机械轴误差对相控阵雷达测角精度的影响。

(1)只存在阵面法向与正北夹角误差Δγ

公式(11)经过计算，可得

(12)

由公式(12)可以看出，雷达方位测角受阵面法向与正北夹角误差Δγ影响，误差为-Δγ，仰角测角不受影响。

(2)只存在阵面倾角误差Δδ

公式(11)经过计算，可得

(13)

可以看出，雷达方位测角误差受方位扫描角A1、仰角扫描角E以及倾角误差Δδ联合调制，仰角测角误差受扫描角A1和安装误差Δδ联合调制。

以下分别仿真分析方位扫描角A1、仰角扫描角E以及倾角安装误差Δδ对方位测角误差和仰角测角误差的影响，结果如图2～4所示。

(a)方位测角误差与方位扫描角关系

(a)方位测角误差与仰角扫描角关系

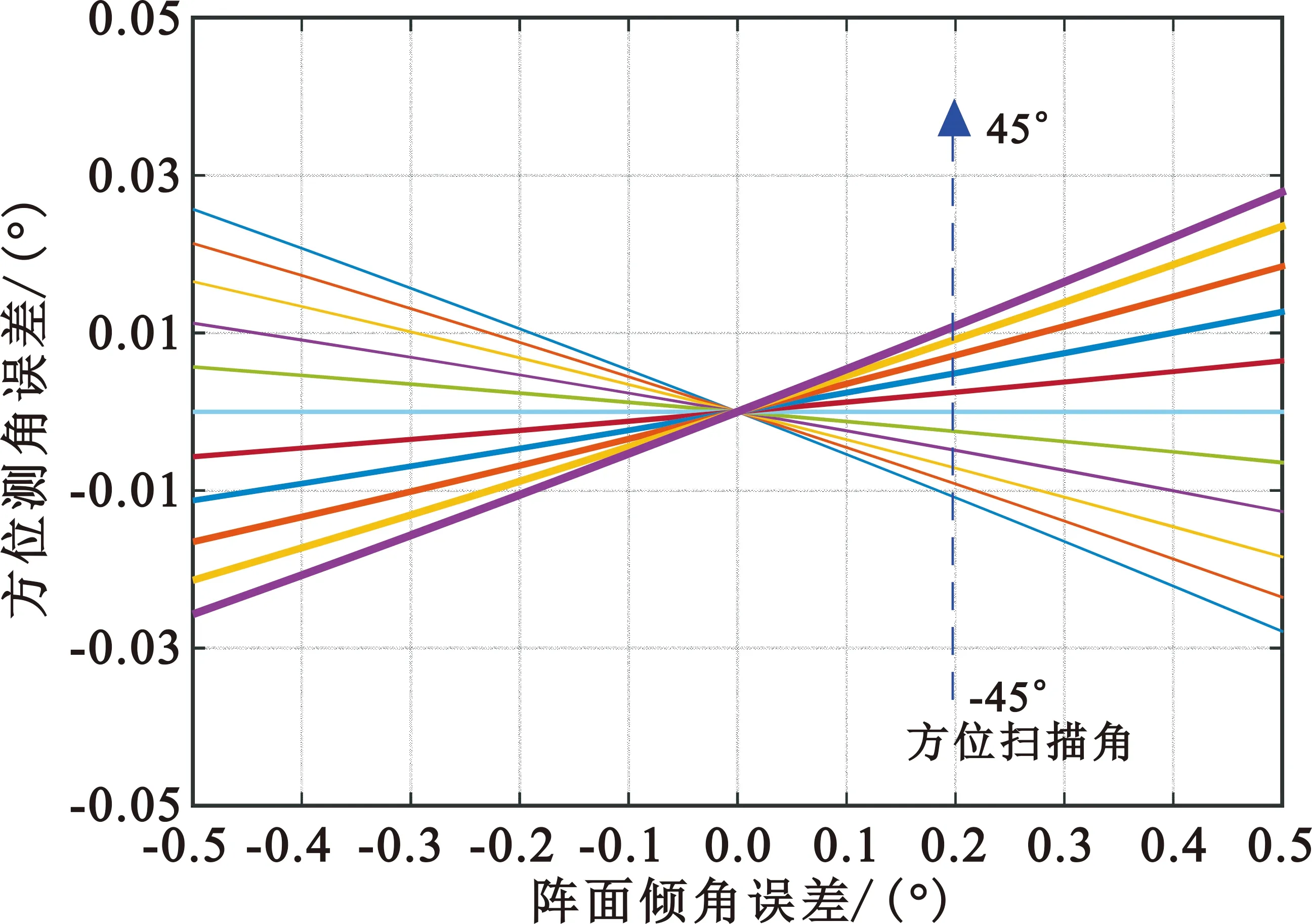
(a)方位测角误差与阵面倾角误差关系

(3)只存在不水平度误差Δσ

公式(11)经过计算，可得

(14)

可以看出，雷达方位测角误差受扫描角A1、E1、阵面倾角T以及不水平度误差Δσ联合调制，仰角测角误差受扫描角A1、阵面安装倾角T和不水平度误差Δσ联合调制。

下面分别讨论仰角扫描角E1、方位扫描角A1、阵面倾角T、不水平度误差Δσ对系统方位和仰角测角误差的影响，如图5～8所示。

(a)方位测角误差与方位扫描角关系

(a)方位测角误差与阵面安装倾角关系

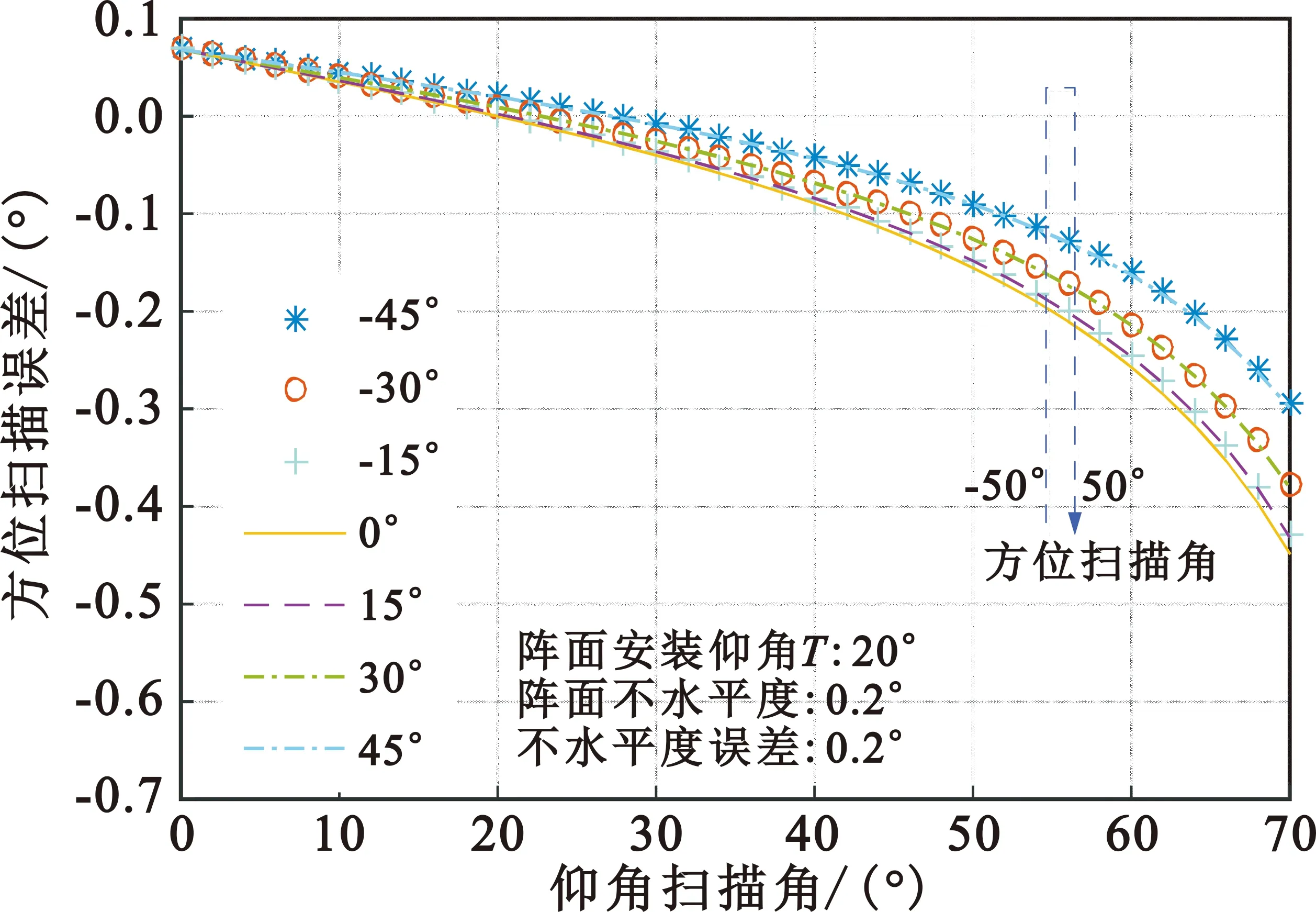
(a)方位测角误差与仰角扫描角关系

(a)方位测角误差与不水平度误差关系

3 机械轴误差解算

方位扫描角位于法向时，ΔA1=0，公式(11)经过计算，可得方位和仰角测角误差分别为

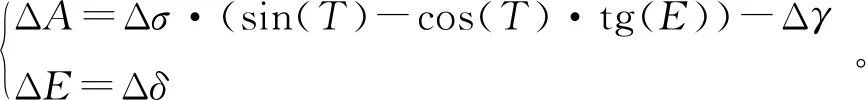
(15)

当目标分别于仰角E1和E2飞越阵面方位法向时，产生方位测角误差和仰角测角误差分别为ΔA1、ΔA2、ΔE1、ΔE2,根据公式(15)可得

(16)

公式(16)中，Δγ、Δσ、Δδ即为阵面机械轴误差。同时，公式(16)也为利用无人机加载差分全球定位系统(Differential Global Positioning System，DGPS)法标校相控阵雷达天线阵面机械轴误差参数提供了理论支撑。

4 机械轴误差验证方法及仿真分析

4.1 无人机加载DGPS系统标校方法

DGPS基本原理是利用已知精确三维坐标的DGPS基准站，求得伪距修正量或位置修正量，再将该修正量实时或延迟发送给用户，对用户的测量数据进行修正，在有效抵消大部分公共误差和选择可用性(Selective Availability,SA)干扰的同时获得更高的GPS定位精度。该技术目前广泛应用于雷达及武器系统精度标校试验[10-11]。本文采用无人机加装龙伯球搭载DGPS标校法验证相控阵雷达天线阵面机械轴误差。选择和安装龙伯球时，应尽量设计成与无人机散射中心重合，以便作为一个“点目标”，在增大目标信噪比、有效减小回波小信噪比造成雷达测量值起伏误差的同时，减少散射点，易于被测雷达稳定跟踪。

4.2 试验航路规划

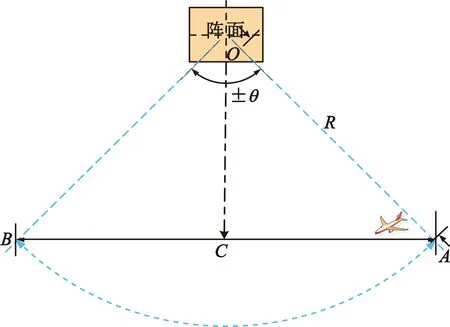
图9 相控阵雷达天线阵面机械轴误差验证航路规划图

考虑雷达低空探测时电磁波多路径效应对系统测角误差的影响[12]，目标靶机飞行仰角应选择高仰角(E>2°)，飞行半径应在雷达威力覆盖范围内并满足误差统计点数要求。

4.3 仿真验证

设定某一相控阵雷达相关机械轴参数为Nt=100°，T=20°，Q=0.2°，Δγ=0.3°，Δσ=-0.2°，Δδ=0.1°，利用图9所示航路图，根据公式(11)进行仿真，得到机械轴综合误差情况下方位和俯仰测角误差随方位扫描角变化关系图，结果如图10所示。

(a)方位测角误差

由公式(16)计算得，阵面法向与正北夹角误差为-0.3°，阵面倾角误差为-0.2°，阵面不水平度误差为0.1°，与预设值一致，验证了方法的可行性。

5 结束语

本文针对相控阵雷达测角误差受天线阵面机械轴误差在多个维度上影响而无固定影响模式，结果难以分析和评估的问题，基于空间直角坐标系到阵面直角坐标系的变换矩阵，对机械轴误差在各个维度上与相控阵雷达测角精度之间的关系进行了详细仿真分析。分析结果表明，机械轴误差对相控阵雷达在不同维度上对测角误差的贡献不同，在设计高精度相控阵雷达时，需对系统各节点误差指标做好评估和分配，波束指向公式需要进行修正。结合变换矩阵，利用方位法向测角误差与机械轴误差的关系，解算出机械轴误差与测角误差之间的简约关系式，提出了一种利用常规雷达精度校飞方法验证机械轴误差的方法，仿真分析结果证明了该校飞方法和简约关系式应用于解算机械轴误差的可行性和有效性。后续将借助实际的相控阵雷达精度校飞试验对该关系式进一步验证和完善。