装配式小箱梁斜交与正交荷载横向分布对比

孙淑梅

（烟台市莱山公路建设养护中心，山东 烟台 264003）

引言

装配式小箱梁桥建筑高度低、施工快捷，具有抗弯刚度、抗扭刚度大、稳定性好和活载作用下受力均匀等优点，得到了快速发展［1-2］。其中，斜交装配式小箱梁桥占据了相当大的比重。

装配式小箱梁桥的荷载横向传递主要依靠现浇湿接缝，结构的横向效应及空间受力特征比较突出，而斜交小箱梁桥与正交桥的受力特性又有较大的不同。目前国内的横向分布计算方法都是只针对单跨简支正交桥，而对于斜交小箱梁桥的荷载横向分布还没有一种成熟的计算方法。

对于斜交小箱梁桥的计算，空间有限元法如果建模得当，能较好地模拟实际桥梁结构的形状及边界条件，所得计算结果能较准确地反映实桥的受力状况。但空间有限元法耗时耗力，同时对从业人员的专业知识的要求较高，且大多斜梁桥的跨径不大，采用空间有限元法计算并不十分合理。

1 工程概况

某高速路 4 座斜交角度不同的装配式小箱梁桥A、B、C、D 斜桥，上部结构均为单孔跨径 30 m 的预应力混凝土简支转连续小箱梁，梁高均为1.8 m，斜交角度分别为 60°、65°、75°、80°；主梁均采用C50 混凝土；设计荷载均为公路-Ⅰ级。桥梁横断面见图1，主梁截面特性见表1。

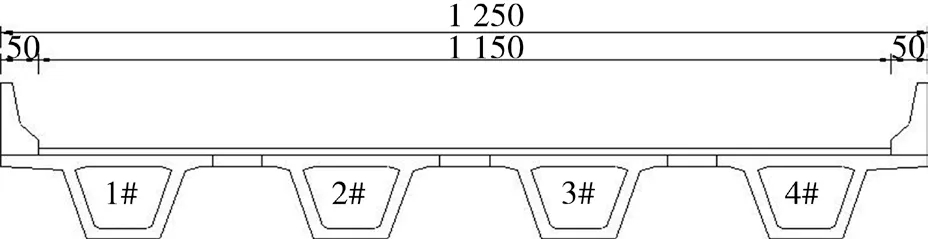
图1 桥梁横断面/cm

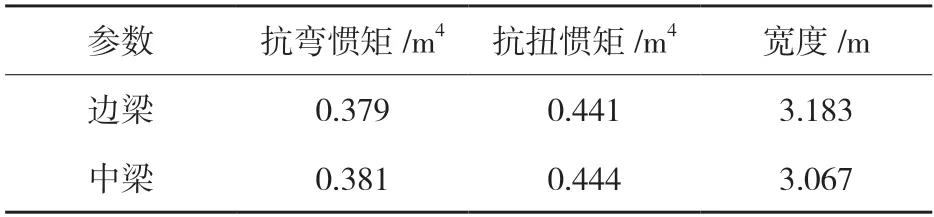
表1 主梁截面特性

2 静载试验实测值

斜桥 A、B、C、D 静载试验均采用 6 辆载重 30 t的三轴卡车，通过对次边跨跨中挠度最不利位置进行偏载加载，测量试验荷载下次边跨跨中的挠度，得到各片小箱梁跨中的横向分布系数。静载试验的车辆加载横桥向布置见图2。

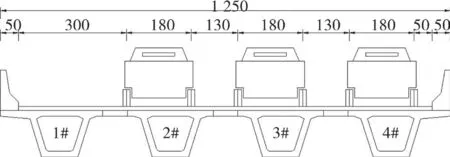
图2 车辆加载横桥向布置/cm

静载试验得到的各桥次边跨跨中挠度实测值见表2，次边跨跨中荷载横向分布系数实测值见表 3。

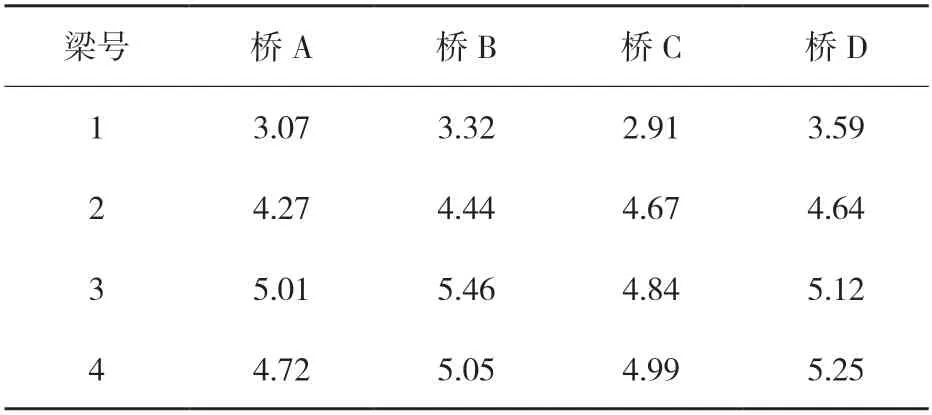
表2 偏载工况次边跨跨中挠度实测值/mm

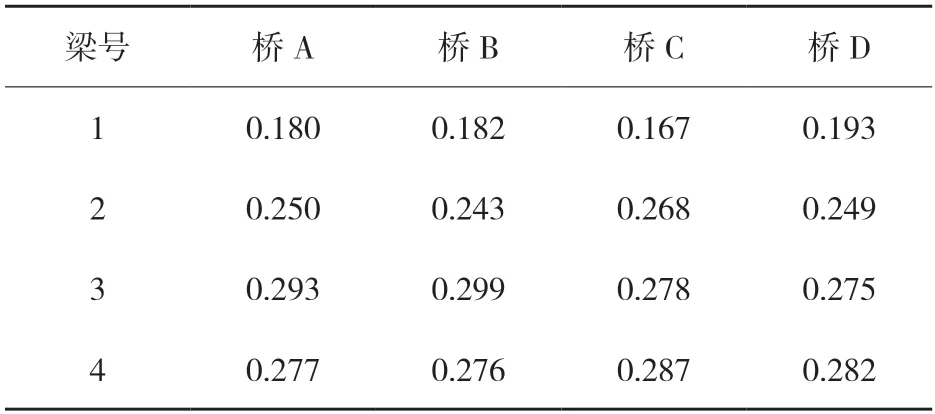
表3 次边跨跨中荷载横向分布系数实测值

3 正交情况下的荷载横向分布理论计算值［3］

由于斜桥 A、B、C、D 结构形式和主梁截面特性均相同，按正交情况计算的荷载横向分布系数相同。计算方法采用刚接板梁法计算得到各片主梁的荷载横向分布影响线，然后根据车辆布载形式得到各片主梁的荷载横向分布系数。计算得到的横向分布影响线和横向分布系数值见表4、表 5。

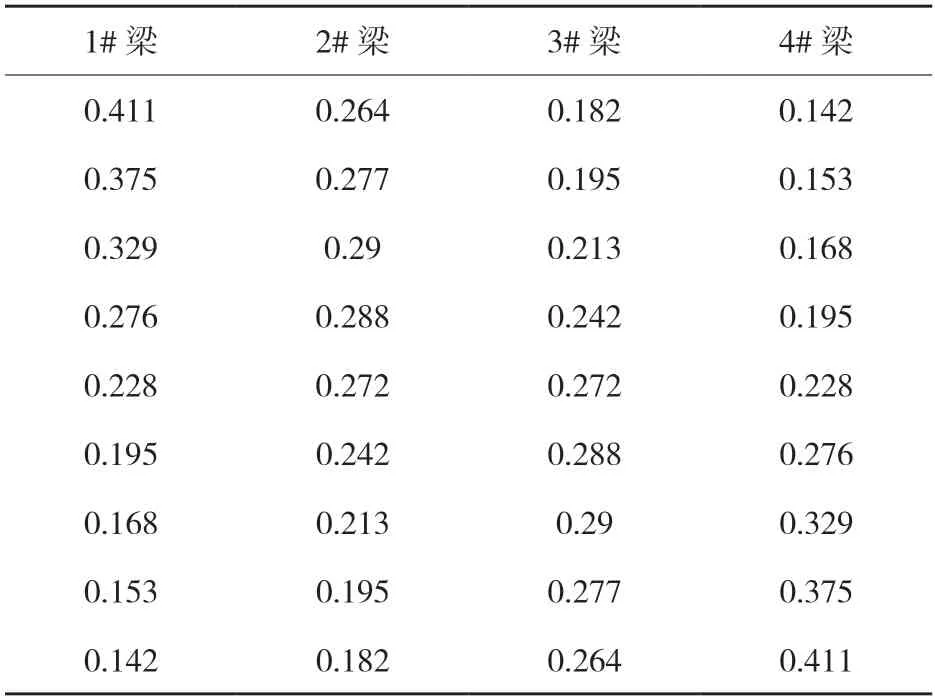
表4 荷载横向分布影响线竖标（正交情况）

表5 荷载横向分布系数理论值

4 对比分析

将静载试验得到各桥荷载横向分布系数实测值与正交理论值进行对比分析，结果见表6、图 3。

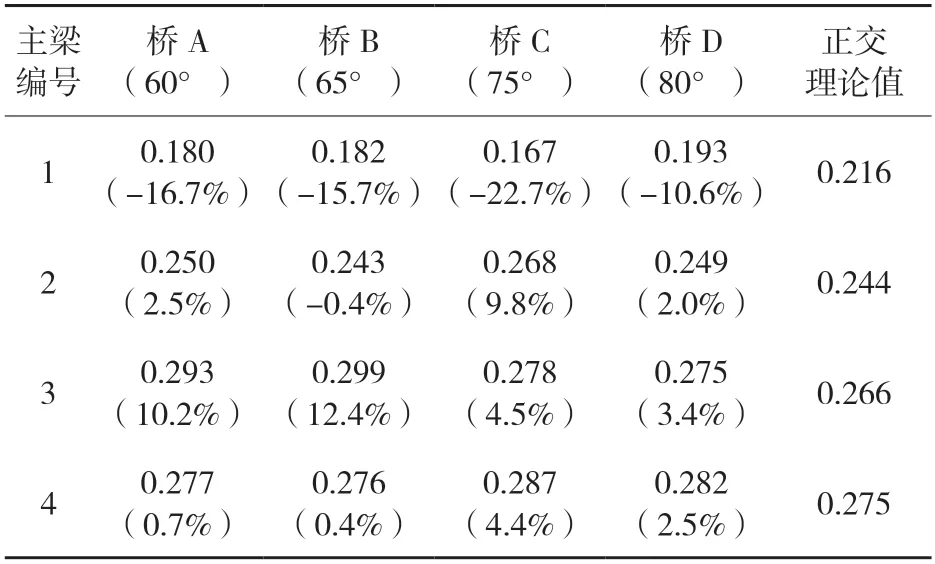
表6 偏载工况次边跨跨中横向分布系数对比

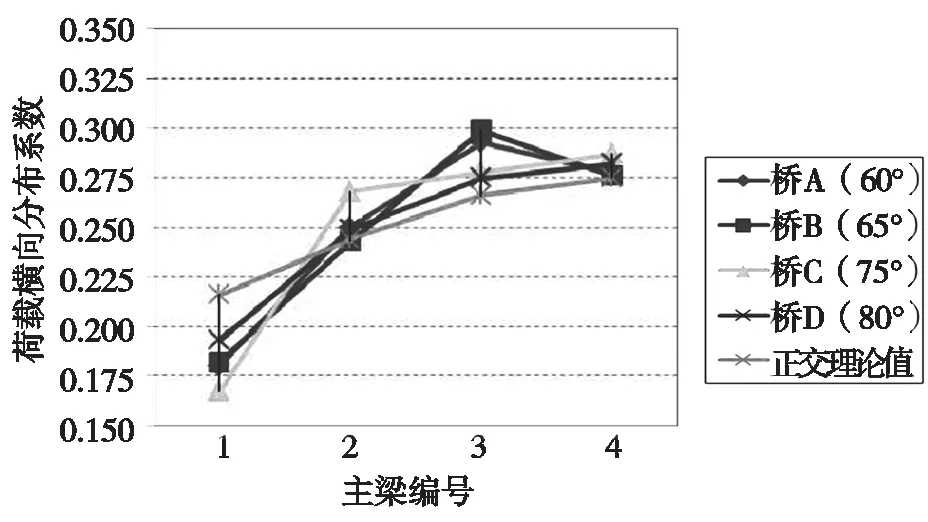
图3 偏载工况次边跨跨中横向分布系数曲线

从表 6 和图 3 可以看出：（1）在相同的偏载作用下，桥 A（60）与桥 B（65）各片梁的横向分布系数比较接近，且分布规律相同，中梁横向分布系数较边梁大；桥 C（75）与桥 D（80）各片梁的横向分布系数比较接近，且分布规律相同，边梁横向分布系数较中梁大。（2）A（60）与桥B（65）各梁的横向分布系数分布规律与正交理论值有较大差异，因此，建议采用空间有限元法进行计算。（3）C（75）与桥D（80）除偏载对侧的边梁外，其余各梁的横向分布系数与正交理论值较为接近，受力最不利的边梁横向分布系数与正交理论值最大偏差不超过 4.4%，偏载对侧的边梁横向分布系数比正交理论值小，按正交理论值计算，结果偏于安全，因此，对于斜交角度 75和 80的斜交小箱梁桥，可近似按照正桥进行计算，满足工程应用需求。

5 结语

（1）桥梁斜交角度越大，受力情况越接近于正桥，根据桥 C（75°）与桥 D（80°）的试验数据分析结果，建议对于斜交角度＞75°的斜交小箱梁桥，近似按照正桥进行计算。（2）根据桥 A（60°）与桥 B（65°）的试验数据分析结果，斜交角度较小的小箱梁桥，受力与正桥有较大差异，谨慎起见，对于斜交角度＜ 75°的斜交小箱梁桥，建议采用空间有限元法进行计算。