四元合金析出行为的非等温傅里叶谱相场模拟
2022-03-26杨芳芳杨斌鑫
杨芳芳,杨斌鑫
(太原科技大学 应用科学学院,太原 030024)
Fe-Cu合金除了是具有重要技术意义的合金系统外,由于彼此之间几乎没有固溶性,因此经常在实验研究中用作模型系统。关于Fe-Cu合金系统中富Cu相的析出顺序有很多研究[1-3]。普遍认为,初始沉淀开始于与铁基体相干的亚稳体心立方(bcc)相[4-6]。在随后的生长和粗化过程中,析出物经历了六方有序相(9R和3R)的断层结构,最终成为Cu的平衡面心立方(fcc)结构[2]。有研究表明其他合金元素(如镍和锰)的存在会导致形成具有富Ni-Mn的金属间B2环和富铜的核的环/核沉淀物形态[7-8]。该热稳定的金属间相的存在阻止了进一步的扩散生长,从而导致稍后富含铜的沉淀物缓慢变粗。此外,金属间B2壳层充当缓冲层,以缓解Cu析出物与Fe基体之间的晶格失配应变。由于Fe-Cu合金在工业中得到了广泛使用,因此概述了几种建模和模拟方法来量化沉淀动力学[9]。CALPHAD(CAL的PHAse图的模拟)数据库已用于Fe-Cu-Mn-Ni系统的热力学描述,以便定量预测在相场公式内旋节线状态下的微观结构演变建模[10]。
由于有限差分法和有限元法具有局部特征,通常未知函数由小子域上的低阶多项式来解释。相反,频谱方法通常使用高阶多项式或傅立叶级数来表示全局[11-12]。频谱逼近的收敛速度仅取决于解的光滑度,与其他两种方法相比,它们以更少的采样点实现了更高的精度。这个事实在很多文献中被称为“光谱准确性”。频谱方法最常在周期性的域中获得成功,这在大多数相场建模仿真中都是如此。傅里叶谱方法作为一种求解偏微分方程的数值计算方法,将偏微分方程的解近似地展开成光滑函数的有限级数展开式,再由此有限级数展开式与偏微分方程,求解得到有限级数展开式的系数方程组。使用傅里叶谱方法求解相场方程,不需要继续计算复杂的九点差分格式的算子,并且对于与周期性边界条件,傅里叶级数的计算更为便捷,谱方法的精度更为准确,相比有限差分方法,傅里叶谱方法的使用大大加快了求解相场方程的运算速度,提高了数值计算与数值模拟的效率[13-17]。
合金的研究一直以来都是各个工业领域研究的重点内容,合金具有硬度大,熔点低,可塑性好等特点。合金对温度非常敏感[18],研究合金与温度场的关系也成了重要课题。本文的目的是在Fe-Cu-Ni-Mn合金系统中利用傅里叶谱方法进行数值求解以及数值模拟,参考傅里叶谱方法在相场方程中的应用[19]。研究了恒温条件下合金析出行为[20],并增加非恒温温度场的条件,观察在此条件下对于四元合金析出行为的影响[21]。得出结论,与恒温条件下相比较,非恒温温度场的条件下合金各元素在温度高的地方的析出更快更明显。
1 相场方程的建立
1.1 相场控制方程
用文献[10]中的Fe-Cu-Mn-Ni体系的公式。由Cahn-Hilliard和Allen-Cahn方程控制的自由能减少驱动的多组分合金系统的微观结构演变:
(1)
(2)
其中ci(r,t)描述合金元素的浓度场(作为空间位置r和时间t的函数)(即,对于Fe,Cu,Mn和Ni分别为i=1,2,3,4)。相场变量η(r,t)表征了Cu沉淀物中α(bcc)和β(fcc)相的相分布,取0 Mi(η,T)= (3) 总自由能F包括因组成和相不均匀性引起的短程相互作用以及长程弹性相互作用,可表示为[10]: F= (4) (5) 在具有磁性贡献的Fe-Cu-Mn-Ni四元体系中,φ相(φ=α或γ)的吉布斯能量函数可以通过次正规解来近似[10]。 (6) (7) 由焓守恒定律导出的温度场T的演化方程: (8) 上式中T无量纲化的温度。τ是一种无量纲潜热,它与潜热成正比,与冷却强度成反比。 通过在式(1)中取函数导数: (9) 通过对式(1)两边进行傅里叶变换得到空间离散化公式: (10) 通过隐式地处理线性和二阶算子,并显式地处理其他项,式(10)的半隐式形式是: (11) 重新排列可得: (12) 其中Δt是n+1和n之间的时间增量,{·}k是括号内数量的傅里叶变换,κ是傅里叶空间中的向量。 通过在(2)中取函数导数: (13) 通过对式(2)两边进行傅里叶变换得到空间离散化公式: (14) 通过隐式地处理线性和二阶算子,并显式地处理其他项,式(14)的半隐式形式是 (15) 重新排列可得: (16) 其中Δt是n+1和n之间的时间增量,{·}k是括号内数量的傅里叶变换,κ是傅里叶空间中的向量。 对温度场方程(8)进行傅里叶谱变换: (17) 式(17)的半隐式形式是: (18) Δt是时间步长n+1和n之间的时间增量,通过重新排列式(18),得: (19) 在具有网格点数Nx=Ny=128的仿真单元,网格点之间的距离dx=dy=0.5,合金标称成分选择为15%的Cu,1%的Ni和1%的Mn中进行仿真。利用傅里叶谱方法对此方程进行了求解,并在此方法的基础上增加了温度场方程,对求解结果进行了数值模拟。结果如下图: 图1展示了合金元素Cu、Mn、Ni以及序参量在恒温T=823 K状态下的时间演变。从图中可以看出Cu的沉淀物先从过饱和固溶体中均匀析出,Cu析出物变得粗大且尺寸增加,Ni和Mn移至Cu析出物与Fe基体之间的界面区域,最终形成了环形/壳层。 图1 合金在恒温状态下的时间演变 图2展示了合金在加入非恒温温度场条件下的时间演变。从结果图中可以看出依然是Cu的沉淀物先从过饱和固溶体中均匀析出,且在加入非恒温温度场的情况下,Cu、Mn、Ni的析出更快;在温度较高的地方,合金元素析出的更快。 图2 合金在加入非恒温温度场条件下的时间演变 推导了由Cahn-Hilliard和Allen-Cahn方程控制的自由能减少驱动的多组分合金系统的微观结构演变方程,进而建立并求解了非恒温温度场方程在合金系统中的模型。得到了非恒温温度场对合金中各元素析出的影响。结果表明:两次模拟中都是Cu的沉淀物先从过饱和固溶体中析出,Mn、Ni随后析出;在此阶段,Ni和Mn是在固溶体和沉淀之间分配。随着时间的行进,对于模拟一,Cu析出物变得粗大且尺寸增加,Ni和Mn移至Cu析出物与Fe基体之间的界面区域,最终形成了环形/壳层。而模拟二中,在相场中加入温度场,可以看出温度随着序参量的变化而变化,进而影响合金的析出。温度场的加入使得Cu析出物变得粗大且尺寸增加,Ni和Mn移至Cu析出物与Fe基体之间的界面区域,最终形成了环形/壳层的过程变得更短暂更快速,且Cu和Ni、Mn在温度较高的地方析出也更快更明显。

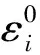
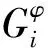
1.2 温度场控制方程
2 用傅里叶谱方法演化相场模型
2.1 Cahn-Hilliard方程的离散化
2.2 Allen-Cahn方程的离散化
2.3 温度场的离散化
3 模拟结果

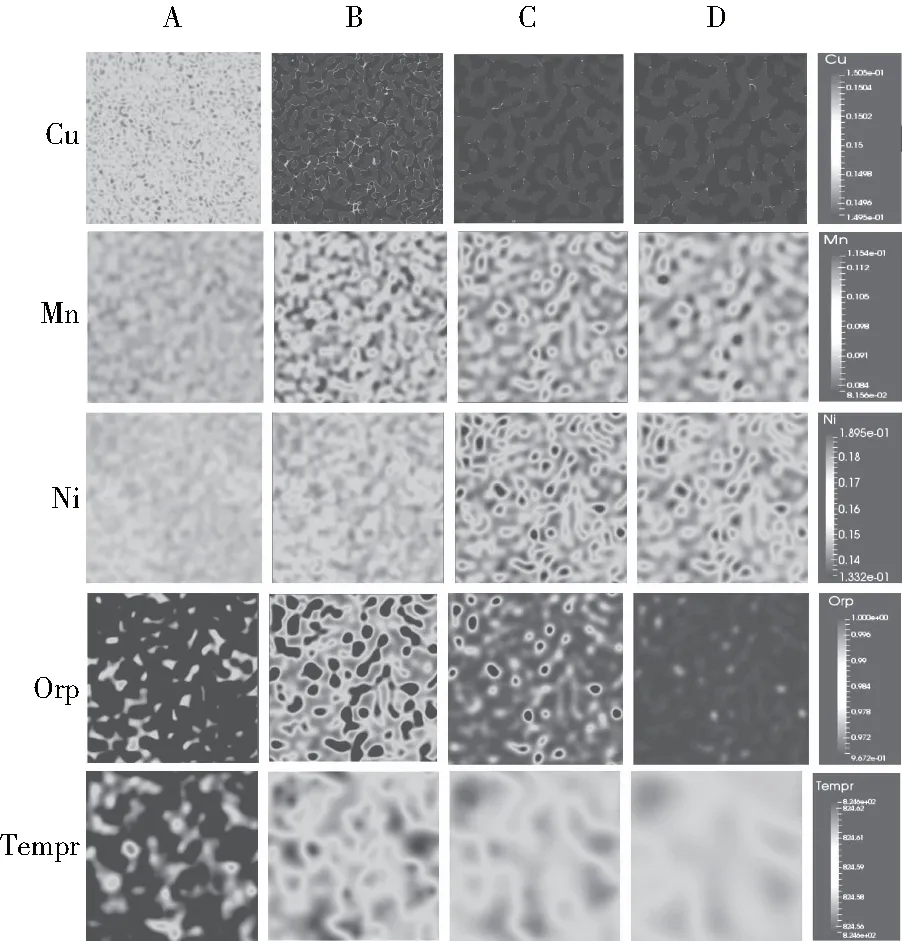
4 结论分析
