圆中相交弦相关性质的推广

安徽省合肥市第八中学合肥市蒲荣飞教育名师工作室(230071)蒲荣飞

圆中有许多优美的性质,本文先给出一个有关相交弦的结论,并从不同视角给出两种证明方法,然后将其类比推广到椭圆.

性质如图1,已知点C是圆O上任一点,以C为圆心作一个圆,其与圆O的直径MN相切于点D,与圆O相交于点A,B,则AB必平分CD.

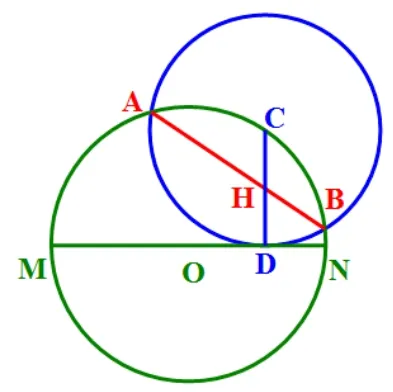
图1

证法1(几何法)如图2,延长线段CD分别交圆C和圆O于P,Q两点,则在圆C中利用相交弦定理可得AH · HB=PH · HD=(PC+CH)· HD=(CD+CH)· HD.在圆O中利用相交弦定理可得AH·HB=CH·HQ=CH·(HD+DQ)=CH·(HD+CD).从而有(CD+CH)· HD=CH ·(HD+CD),即CD ·HD+CH ·HD=CH ·HD+CH ·CD,也即CH=HD,故AB平分CD.

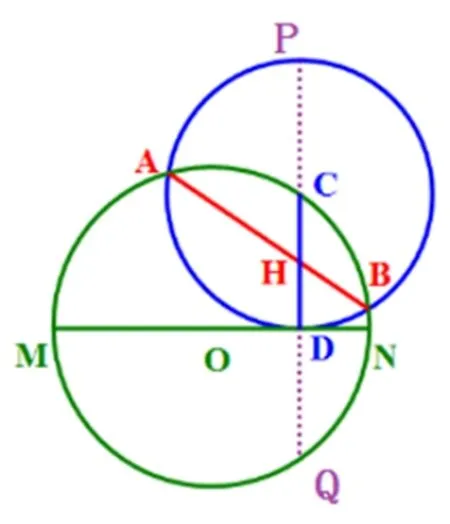
图2

证法2(解析法)如图3,以O为坐标原点,以线段MN所在直线作为x轴,以其中垂线为y轴,建立如图所示的平面直角坐标系.设点C(x0,y0),则线段CD的中点于是,圆C的方程为圆O的方程为x2+y2=R2.两方程相减得公共弦AB所在直线方程为中点满足上方程,故AB平分CD.

图3

众所周知椭圆可看作由圆通过伸缩变换而得到的,圆也可以看作是椭圆的极端图形,那么将该性质中能类比推广到椭圆呢? 由于两个圆必是相似的,为了叙述方便,先给椭圆相似下个定义.

定义形如与的椭圆称为同位相似椭圆,λ称为其相似比.

显然同位相似椭圆的离心率相同,焦点所在坐标轴也相同.于是,上性质类比到椭圆可以得到

推广如图4,已知点C是椭圆O上任一点,以C为中心作一个与椭圆O同位相似且与其长轴MN相切于点D的椭圆C,并且与椭圆O相交于点A,B,则AB必平分CD.

图4

图5

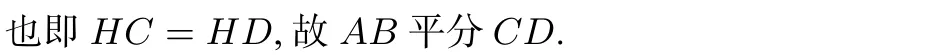
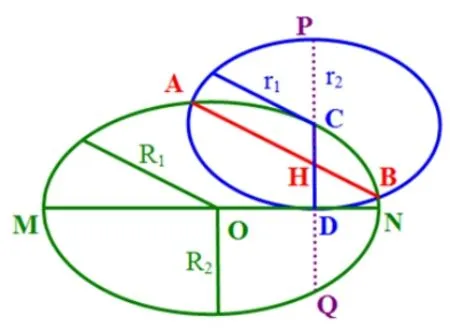
图6

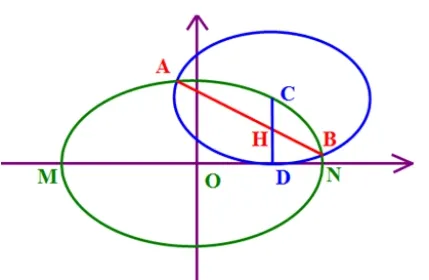
图7