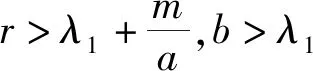比率依赖的修正Leslie-Gower捕食-食饵模型正解存在性和唯一性
2022-03-25窦晓霞,李海侠
窦 晓 霞, 李 海 侠
(宝鸡文理学院 数学与信息科学学院,陕西 宝鸡 721013 )
0 引 言
捕食-食饵模型是生态学与生物数学的一个重要研究课题,具有丰富的动力学行为,已成为生态领域研究的核心内容,受到了国内外数学家和生物学家的广泛关注.生物模型中反应函数的引入提高了有实际背景生物模型的精确度,因此,生物学家和数学家建立并研究了具有不同反应函数的捕食-食饵模型.这些研究包括经典的Holling-Ⅱ型[1-5]、比率依赖型[6-7]、Beddington-DeAngelis型[8]、Crowley-Martin型[9-12]和Ivlev型[13-14]等反应函数.现实中随着食饵数量的增加,食饵的防御能力也会提高,这对捕食者会起到抑制作用.于是为了模拟这种抑制现象,Andrews提出了Holling-Ⅳ型反应函数.文献[15]讨论了具有简化Holling-Ⅳ型反应函数的捕食-食饵扩散模型,利用分歧理论得到了正分歧解的存在性和稳定性,并通过不动点指数理论给出了正解的存在性.文献[16]考察了具有Holling-Ⅳ型反应函数的捕食-食饵模型,讨论了稳态解的存在性和稳定性、倍周期分歧和Neimark-Sacker分歧的存在性和方向.本文主要考虑一类基于比率依赖的简化Holling-Ⅳ型反应函数的捕食-食饵扩散模型,运用反应扩散方程和非线性泛函分析等理论,通过考察食饵和捕食者的增长率以及捕食者的捕获率等因素的影响来研究该模型的动力学行为.
1 模型介绍
文献[17]在齐次Neumann边界条件下讨论了如下比率依赖的Leslie-Gower捕食-食饵模型:
(1)
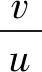
考虑到捕食者和食饵受空间非均匀分布的影响,本文在Robin边界条件下研究如下修正Leslie-Gower 捕食-食饵扩散模型:
(2)
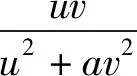
从生物学的现实意义上来讲,物种是否能够共存是对生物模型最重要的研究内容之一.因此本文重点讨论系统(2)对应的平衡态系统
(3)
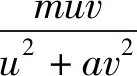
为了得到重要的结论,给出本文需要的预备知识.
令λ1(p)是特征值问题
易知当r>λ1时,如下方程
(4)
存在唯一正解,记为θ(r,a).而且,θ(r,a) 利用不动点指数理论讨论系统(3)正解的存在性. 易知:当r>λ1时,系统(3)存在半平凡解(θ(r,r/k),0);当b>λ1时,系统(3)存在半平凡解(0,θ(b,b/c)).简单起见,记θ(r,r/k)为u*,θ(b,b/c)为v*. 首先,运用特征值的比较原理以及最值原理易得正解存在的必要条件和先验估计. 引理1若系统(3)存在正解(u,v),则r>λ1,b>λ1. □ □ 为了计算不动点指数,引入以下记号: 下面在{(u,v):u≥0,v≥0}上定义函数 定义算子F:D′→W为 这里M是满足M>max{m/a,b(k+c)/c}的充分大的常数.于是F是紧且连续可微算子.显然系统(3)存在非负解当且仅当算子F在D中存在不动点. 接下来运用文献[21]中的定理1给出算子F在平凡解和半平凡解处的不动点指数. 引理3设r>λ1,b>λ1,则 以及算子Fε为 证明首先证明(0,0)是F在W中的孤立不动点.假设不成立,则存在非负非平凡解Wi=(ui,vi),使得当i→∞时Wi→(0,0)且(I-F)Wi=0.于是ui、vi满足 □ 最后由引理3并结合不动点指数的可加性可得系统(3)正解存在的充分条件. 则 因此系统(3)至少存在一个正解. □ 本章分析参数m对系统(3)正解唯一性和稳定性的影响,给出正解唯一且稳定的条件. 若r>λ1,b>λ1,则问题 存在唯一正解,记作v*. 2.1 一般资料比较 本研究辅助生育组孕妇140例,孕周:15+0~15+6周 27 例,16+0~16+6周 65 例,17+0~17+6周29例,18+0~18+6周13例,19+0~19+6周6例,年龄(30.73±3.40)岁,体重(56.56±8.43)kg;自然妊娠组孕妇420例,孕周:15+0~15+6周32例,16+0~16+6周178例,17+0~17+6周154例,18+0~18+6周42例,19+0~19+6周14例,年龄(29.32±4.11)岁,体重(54.67±8.55)kg,差异无统计学意义(P>0.05),具有可比性。 x∈Ω (5) (6) 如果ξ≢0,则由式(6)可知 矛盾,故ξ≡0.于是 此矛盾说明结论成立. □ 故结合引理4得到系统(3)存在非退化且线性稳定的唯一正解. □ 本章通过抛物方程的比较原理探讨系统(2)的灭绝性和持久性.首先探讨半平凡解(u*,0)和(0,v*)的稳定性. 引理5(i)设r>λ1.如果b<λ1,则半平凡解(u*,0)稳定;如果b>λ1,则半平凡解(u*,0)不稳定. 证明由于(i)和(ii)的证明类似,因此只证明(ii).考虑系统(3)在(0,v*)处的线性化特征值问题: (7) □ 其次给出系统(2)灭绝的充分条件. 定理3设(u,v)是系统(2)的正解.如果r≤λ1,b>λ1,则当t→∞时,(u,v)→(0,v*). 证明因为 由比较原理得,当t→∞时,u(x,t)→0.令是充分小的正常数,则存在T≥0使得所有t>T有u(x,t)<.由系统(2)的第二个方程得 于是 (8) 又由系统(2)的第二个方程得 再由比较原理有 (9) □ 最后给出系统(2)的持久性条件. (10) 和方程 (11) (12) v(x,t)≤v*+ (13) 另一方面,由系统(2)有 根据比较原理可得 于是存在T″≥0使得对于所有的t>T″,有 (14) 设T*=max {T,T′,T″},则对所有的t>T*,有 □2 正解的存在性
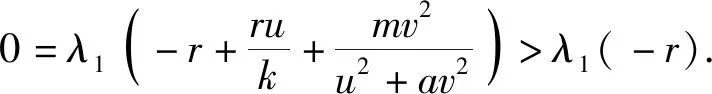
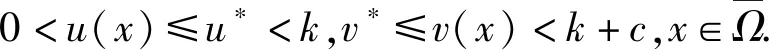
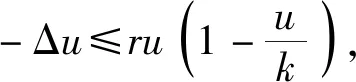
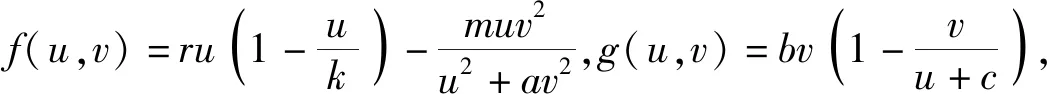
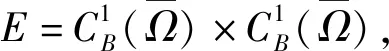
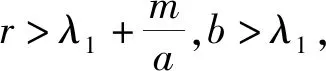

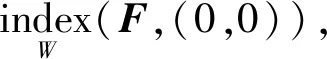
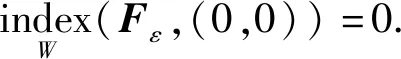
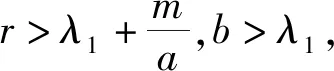
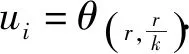
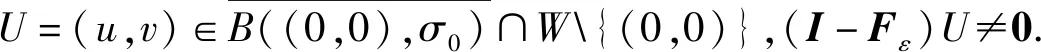
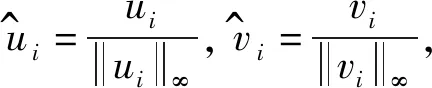

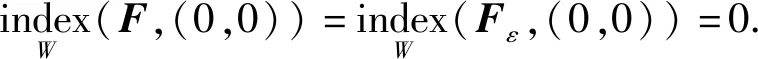
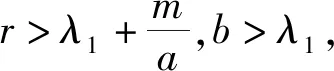
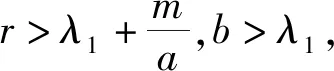
3 正解的唯一性和稳定性
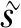
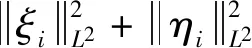
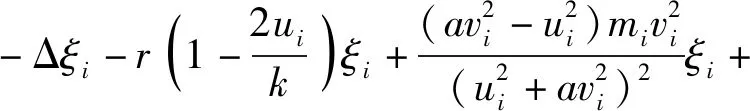
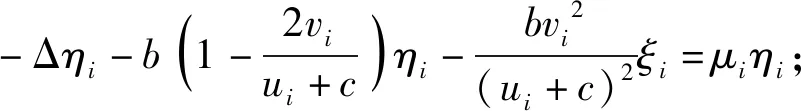
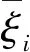
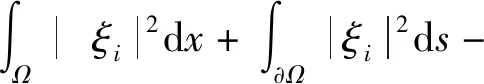
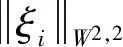
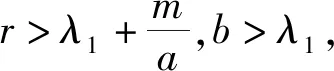
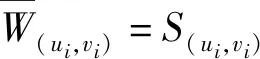
4 半平凡解的稳定性和渐近行为
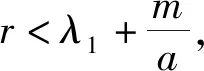
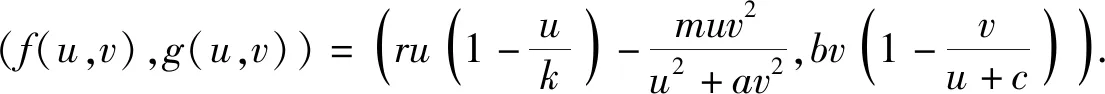
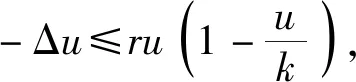
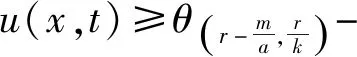
5 结 语