探寻规律本质 促进深度理解
2022-03-25何海华
何海华




【摘 要】学生学习数学规律时,必须结合已有经验,深入探索其本质,才能真正地理解。本文以“商的变化规律”为例,进行了前期的调查摸底,从学生的现状出发来凝视问题,针对此类问题,从学习内容的安排、学生的心理特点和教学处理方式等方面进行了深度分析思考,研究有效的教与学策略。通过整合内容、猜想验证、对比联系、多元表征等多种策略引导学生探究商的变化规律,促进学生对规律的深度理解,发展学生的核心素养。
【关键词】数学规律 深度理解 策略研究
一、问题凝视
苏教版数学四年级上册学习了“商不变的性质”后,练习册中有这样一道练习题:
根据5400÷18=300,直接写出下面各题的答案。
540÷18=( ) 5400÷36=( )
270÷18=( ) 5400÷72=( )
笔者下学期开学初进行了调查测试:随机选择了2个班,共计83人,全部正确26人,占比31.3%;错误47人,占比56.6%;未完成10人,占比12%。这样一道填空题,正确率才三成,甚至还包括直接列竖式计算的。错误答案则五花八门。从学生卷面痕迹来看,有部分学生没想到用商的变化规律来思考,有些学生是运用规律来填空的,但由于对规律的理解不够透彻,因此找不准其中的规律。此类题目,教师们也反馈,学生掌握不好,虽反复讲评,效果仍旧不佳。
二、成因透视
(一)内容编排的问题
本内容涉及的知识点是商的变化规律。苏教版数学四年级教材中,只有商不变的性质,没有安排商的变化规律的例题,练习中却时有出现。人教版数学教材中有编排,是把商不变的性质和变化的规律安排在一课时中学习的。商的变化规律需要学生从静态思考走向动态思考,这也是学生思维从运算走向关系的一个转折过程。它与后续学习的常见数量关系、分子分母的变化、比的前项后项变化、正反比例意义,乃至中学的正反比例函数都有着千丝万缕的联系。
(二)规律理解表面化
四年级学生正好处于具体形象思维向抽象逻辑思维的过渡时期。学生要通过一大堆静态的数学算式来学习动态的变化规律,对于静态思维的学生来说,存在一定困难。所以学生对这种动态变化规律的理解只能浮于表面。没有对规律进行深入的探索与思考,不与学生的生活经验对接,要在变与不变中真正理解商变化规律的本质,有一定的难度,学习很难真正地发生。
(三)教學处理简单化
教学中,教师一般都是让学生通过观察一大堆的算式,比较归纳得出规律,并且在商不变的性质内容方面花费时间较多,即所谓的重点。而对于商的变化规律,教材上没有例题,没有单独安排,即使补充了教学内容,往往也是一带而过,觉得只要熟背三条规律就好。这种重结果轻过程的教学方式也直接导致学生对变与不变规律一知半解。还有个别教师认为这仅仅是一道习题,学生实在不会可以列竖式计算,只要算对就好。这是纯粹的应试教育。本课的教学目标有探索发现规律、渗透函数思想、培养抽象概括能力等,如果采用简单的灌输式教学,学生的创新思维、核心素养的培养都是空话。
三、出路审视
(一)整合内容,突破难点
不安排商的变化规律的教学,显然不合适。仅仅作为练习题一带而过,讲解不到位,学生学得也不扎实。把被除数、除数的变化引起商的变化的三个规律合并在一课时中教学,学习的内容太多,也不够深入,学生学起来有一定难度。因此,笔者建议重新整合内容,统筹安排两个课时,“商不变的性质”为第一课时,“商的变化规律”为第二课时。这样的整合安排可以适当分散学习难点,丰富了学习内容,也有更多的时间让学生去探索规律,让研究更加深入。
(二)猜想验证,合作探索
猜想—验证是数学学习的重要方法,它能促进学生积极思考、自主探究,培养学生创新意识。教学中,教师要积极营造民主宽松的学习氛围,引发学生的主动猜想。如果仅仅靠几个算式,让学生观察比较来学习商的变化规律,这样的探索是假研究,是填鸭式的被动学习。因此,上课开始就可以放手让学生去猜想:上节课我们研究了商不变的性质,知道了“在被除数和除数同时乘或除以同一个数(零除外),商不变”的性质。那么,除法中的变与不变还有什么规律?如果除数不变,被除数和商有怎样的变化规律?如果被除数不变,除数和商有怎样的变化规律呢?你们的这些猜想是否都正确,怎么办呢?请你想办法来证明,组织小组合作学习,探索验证方法,看看哪组的方法多。让学生明确目标后,教师要引导学生大胆猜想,积极思维,合作探究,给予学生充分的时间和空间,让他们自主地去发现规律、研究规律、归纳规律。
(三)多元表征,促进理解
中年级学生的抽象思维能力还处于初步发展阶段,被动引导学生进行抽象推理,学生理解有困难,教学效果不佳。教学中只有充分激发学生的主观能动性,调动他们的已有知识经验,将已有知识与新的知识产生联系,学生对规律的抽象推理才能水到渠成。初步猜想了商的变化规律,教师可以引导学生通过融入事例、图形表征、计算举例等方式去验证自己的猜想。在多元化的表征验证中,学生会逐步沟通已有知识基础,联结生活经验,迁移同化新知,从而深入理解动态的变化规律。
(四)对比沟通,联结成网
三条规律格式是差不多的,学生比较容易混淆,只有把散状的三条规律串联起来,把知识点的内在联系找出来,学生的知识才能形成网络。课的结尾部分,出示三条规律,引导学生比一比,找一找今天学的商的变化规律与商不变的性质之间的联系。通过比较沟通,学生发现把这两条连起来就是商不变的规律。这样的教学使学生不仅关注规律,而且理清了三条规律背后的联系,从而对商不变的规律理解得更深刻、掌握得更牢固。
四、教学片段重构
(一)设疑导入,猜想规律
师:同学们,我们已经学习了被除数和除数同时乘或除以同一个数(零除外),商不变的性质。如果被除数和除数不同时扩大(或缩小)相同的倍数,商会发生怎样的变化呢?请你大胆猜一猜。
根据学生猜想整理板书如下情况:
(二)多元表征,理解规律
师:你们的这些猜想是否都成立?你们有什么办法来证明?看看哪个小组办法多?
学生合作探究,教师巡视。
1.验证第一组猜想:除数不变,被除数和商的变化情况。
师:接下来我们来研究除数不变的情况,哪个小组先来展示?
生1:我们举个购物的例子,一支水笔5元,我有10元,可以买2支,10÷5=2;如果我有20元,可以买4支,20÷5=4。所以我们认为第一个“除数不变,被除数乘几(除以几),商就乘几(除以几)”的猜想是正确的。第二个不成立。
生2:
生3:我们组是画图来验证的。
8个正方形排成2行,每行4个,8÷2=4;如行数不变还是2行,正方形有16个,每行就是8个,16÷2=8。我们发现,被除数与商的变化是一致的。
生4:……
师:像这样的例子很多,那在除数不变的情况下,能举出被除数与商的变化不一致的例子吗?看来同学们的第一个猜想是成立的。(板书,生齐读!)
2.验证第二组猜想:被除数不变,除数和商的变化情况。
师:如果被除数不变,又是哪个猜想成立呢?
生1:我们小组认为第4个是成立的。举个例子,24个苹果,如果平均分给2人,每人12个;如果分给4人,每人6个;如果分给8人,每人3个。分得人越多,每个人分到的个数就越少。
师:生活中这样的例子还有很多。
生2:我们组是通过列式计算来证明的。
①36÷2=18
②36÷4=9
③36÷12=3
从算式①到算式②,除数2到4乘了2,商从18到9反而除以了2。
师:那第③个算式呢?
生2:从算式②到算式③,被除数没变,除数乘3,商反而除以3。
师:“反而”这个词用得好。这就说明了当被除数不变,除数和商的变化是相反的。
生3:我们组通过画图来证明第4个猜想成立,第3个不成立。
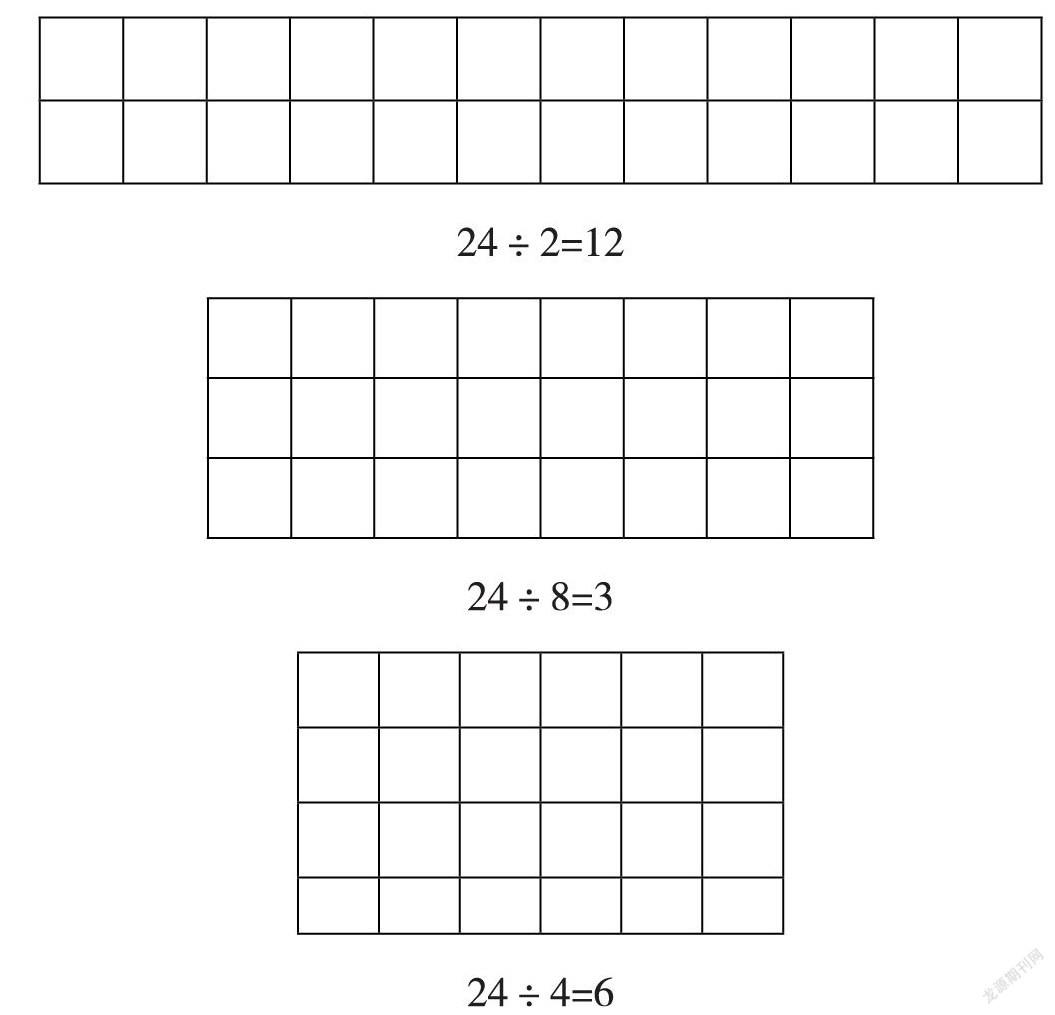
24÷2=12
24÷8=3
24÷4=6
长方形面积相当于被除数,假如长方形的面积24不变,长变小,宽就变大了。
师:看来通过长方形的面积公式也能证明这个规律。 猜想4也是成立的。
(三)對比沟通,深化规律
同时出示三条规律:
师:同学们,三条规律之间有什么联系吗?同桌说一说。
生:我认为今天学的第二条和第三条规律,合起来就是第一条商不变性质。
师:是吗?谁能来具体说一说?
生1:根据今天的学习,如果被除数乘3,商也要乘3;而除数乘3的话,商要除以3,商先乘3再除以3正好抵消,保持不变。
生2:商先乘3再除以3就抵消了。
师:完全正确!商乘3再除以3正好抵消,所以商不变。你们打算怎样记住这三条规律?
生:只要掌握第二、第三条,第一条自然就记住了。除数不变,被除数乘几,商就乘几。被除数不变,除数乘几,商反而除以几。当被除数和除数同时乘几时,商先乘几再除以几,那就肯定抵消掉,商不变。
师:那我来考考大家,A÷B=12,如果A除以6,B乘2,商是多少?
生:被除数除以6,商要除以6;除数乘2,商反而除以2,所以12除以6再除以2商等于1。
师:同学们很厉害!看来只要掌握商的变化规律,不管题目如何变化,都能轻松应对,万变不离其宗!
【参考文献】
[1]中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]皮亚杰.皮亚杰教育论著[M].北京:人民教育出版社,2015.
[3]格兰特·威金斯.追求理解的教学设计[M].上海:华东师范大学出版社,2013.
[4]王光明,范文贵.新版课程标准解析与教学指导[M].北京:北京师范大学出版社,2012.
