画圆求解 简单快捷

刘冰

解决综合性、技巧性比较强的平面几何问题，若能根据题目的特征，联想到圆的有关知识，恰当地构造辅助圆，往往可化繁为简，化难为易，找到简捷的解题途径.下面举例说明.

一、已知圆心和半径作圆

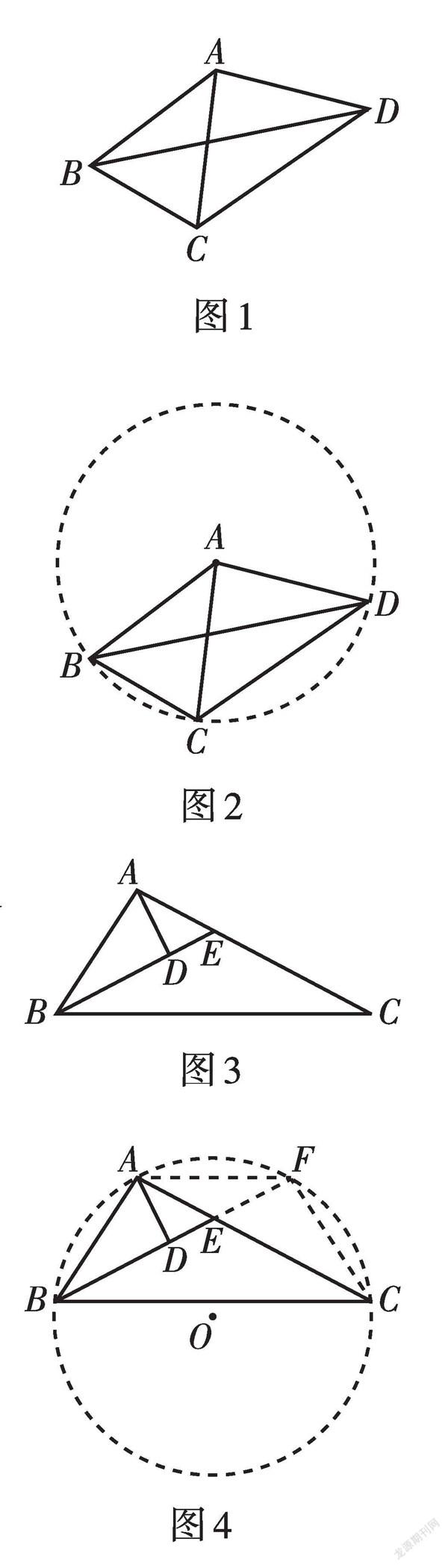
例1 如图1，已知AB = AC = AD，∠CBD = 2∠BDC，∠BAC = 44°，则∠CAD的度数为 .

分析： 由AB = AC = AD可联想到圆的定义，构造以点A为圆心、AB为半径的圆，借助同弧所对的圆周角相等来求解.

解： 如图2，以点A为圆心，AB为半径作⊙A.

∵∠CBD = 2∠BDC，∠CAD = 2∠CBD，∠BAC = 2∠BDC，

∴∠CAD = 2∠BAC.

∵∠BAC = 44°，∴∠CAD = 88°. 故填88°.

點评： 共端点的等线段问题，常作以公共端点为圆心、等长线段为半径的圆，然后利用圆的有关性质使问题迅速获解.

二、作三角形外接圆

例2 如图3，在锐角三角形ABC中，已知∠ABC = 2∠C，∠ABC的平分线BE与AD垂直，垂足为D. 若BD = 4 cm，求AC的长.

分析： 根据∠ABC = 2∠C，可构造△ABC的外接圆，借助圆周角定理及弦、弧之间的关系求解.

解：如图4，过A，B，C三点作⊙O，延长BE，交圆于F，连接AF和CF. ∵∠ABC = 2∠ACB， BE平分∠ABC，∴∠ACB = ∠ABF，∵∠AFB = ∠ACB，∴∠ABF = ∠AFB， ∴AF = AB. 又∵AD⊥BF， ∴BD = FD = 4 cm， ∴BF = 8 cm. ∵∠CBF = [12]∠ABC = ∠C. ∴[⌒][CF] = [⌒][AB]，∴[⌒][CFA] = [⌒][BAF]， ∴AC = BF = 8 cm.

点评： 共顶点的等角问题，常作以公共顶点为一个顶点的三角形的外接圆，从而使等角与辅助圆中有关角的性质建立起联系，使问题得以简捷解决.

（作者单位：山东省枣庄市第四十一中学）