悬链线型海洋脐带缆涡激振动响应分析
2022-03-24乐奇郭一柱王刚张慧甍樊耀华赵佳阳
乐奇,郭一柱,王刚,张慧甍,樊耀华,赵佳阳
1.哈尔滨工程大学 机电工程学院,黑龙江 哈尔滨 150001
2.中航宝胜海洋工程电缆有限公司,江苏 扬州 225101
3.大连交通大学 土木工程学院,辽宁 大连 116028
地球表面面积约有百分之七十是海洋,海洋 内拥有丰富的油气资源[1]。而深海油气资源的采集往往依托水下生产系统,其中脐带缆[2]是不可或缺的关键装备之一。脐带缆是传输化学药剂、电信号等物质[3]的重要远程通道,与海洋油气的采集有着密切的联系。由于海洋内的环境复杂多变,这些复杂的海洋环境如海流流速和浪流流速,在特定流速下的海流流经脐带缆时会诱发其产生涡激振动(vortex-induced vibration,VIV)现象,涡激振动会对海洋脐带缆造成疲劳损伤[3],从而引发脐带缆破坏进而造成生产事故。因此需要考虑复杂的海洋环境因素,其中特别要关注海流流速[4]对脐带缆的影响,它是涡激振动产生的最为直接的原因。近年来国家对海洋工程[5]的研究越来越重视,脐带缆的应用也越来越多,而脐带缆所处的海洋环境以及自身的结构特点容易诱发涡激振动现象,因此对脐带缆的涡激振动现象进行深入研究显得十分必要。
本文针对某悬链线型海洋脐带缆[6],通过改变海洋流速研究涡激振动对脐带缆的影响,针对已有的海洋工况,考虑脐带缆本身的物理参数[7],如脐带缆的外径、弯曲刚度、拉伸刚度等,以及影响上述参数的脐带缆铠装层数[8],从而研究不同铠装层数的脐带缆对抵御海洋涡激振动的影响。结合不同的海洋工况进行研究分析,并相应地提出对脐带缆结构设计的改进措施。
1 涡激振动的基本理论
根据研究立管的经验[9],像立管及脐带缆这种具有圆形截面的柱体在海流作用下常常会发生振动现象。这是因为当流体绕过圆柱体时,会发生边界层分离,从而在结构后面形成尾流区[10],并且在一定条件下从结构两侧周期性地发生旋涡泄放现象。随着漩涡的生成和泄放,圆柱体会受到来自横向和水流方向的脉动压力。如果此时柱体是弹性支撑[11]的状态,则这种脉动方向的力会使柱体产生振动,而柱体的振动又会反作用于尾流结构,导致结构的改变。这种流体与结构之间相互影响作用的问题就是“涡激振动”[12](如图1 所示),当旋涡脱落频率和圆柱体的固有频率十分接近时,就会产生频率锁定的现象。在锁定的区域内,圆柱体会产生大量并且是具有危险的涡激振动响应[13],产生的这种响应会对结构造成很严重的损害。
图1 涡激振动
1.1 脐带缆VIV 计算原理
将整根悬链线型的脐带缆简化为轴向圆柱体[14],上下两端连接海面浮式平台与海底,模型如图2 所示。
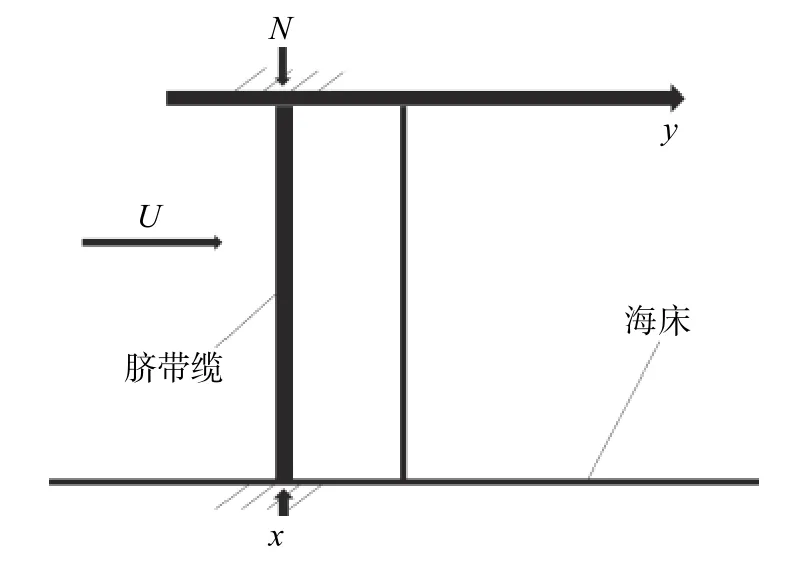
图2 脐带缆简化模型
式中:EI为弯曲刚度,N/m2;N为外界施加在脐带缆上方的顶端张力,kN;m为脐带缆的质量,kg;U为作用在垂直轴向的外界载荷,kN。
采用分离变量方法,对式(1)进行求解,考虑轴向力,得到的振型函数 φ(x)为
结合图2 脐带缆顶端所处的边界条件,将整根脐带缆近似地看作上下两端固定的梁模型,根据梁模型来求解式(2)中的相关的系数,接着求出脐带缆的n阶固有原频率 ωn的表达式:
式中:n=1,2,3,4,…;l为脐带缆的长度,m。
从式(3)可以看出,随着顶端张力N的增大,脐带缆的自身频率也会随之增大,说明顶端张力会对脐带缆的固有特性造成影响。
1.2 尾流振子模型选择
将流体的尾流视为一个非线性振子,采取尾流振子模型对脐带缆进行涡激振动的数值模拟计算[15]。尾流振子只是一个抽象的概念,与其相对应的是漩涡交替脱落的尾迹特征[16],这种特征可用一个隐藏的流场变量[17]表示,与流动的横向流量分量加权平均相关联,并且随其结构所受到的升力变化而变化。尾流振子的运动采用无量纲v来表示,Vanderpol 方程形式的尾流振子振动方程为
式中:ε为Vanderpol 参数;ωf为来流作用下静止圆柱的漩涡脱落频率,Hz;f为振子无量纲受力,表达式为
无量纲的流体振子振动方程为
根据流固耦合[18]的作用力与其反作用力在数值上相等的原则,其作用力的数值包括2 部分,分别是结构反作用力和流体附加质量的反作用力。尾流振子受力F为
式中:CA为附加质量系数;U为水流速,m/s;Y为横向振幅,m;V为流体相对脐带缆的流速,m/s。根据式(4)尾流振子模型的受力F进而分析脐带缆所受涡激振动的影响程度。
Milan 和Iwan-Blevins[19]这2 种尾流振子模型是目前国际研究分析涡激振动软件最常采用的模型。这2 种模型采用的均为时域分析的方法,均用于动态研究分析中,因此在设置动态涡激振动模型的研究中可采取尾流振子模型的方法。需要注意的是,Milan 模型适用于均匀流场中的脐带缆研究,但对于预测固定端节点涡流力的情况并不适合。沿着脐带缆轴向流速的方向,变化的流体速度导致该模型的结构不精确,偏差较大,所以在流速较大并且不均匀[20]的情况会优先考虑使用Iwan-Blevins 模型[21]。基于以上考虑,本文研究采用Iwan-Blevins 尾流振子模型。
1.3 Iwan-Blevins 尾流振子模型
1978 年lwan 和Blevins 提出了较前人相比更加完善的尾流振子模型,即Iwan-Blevins 尾流振子模型,如图3 所示。
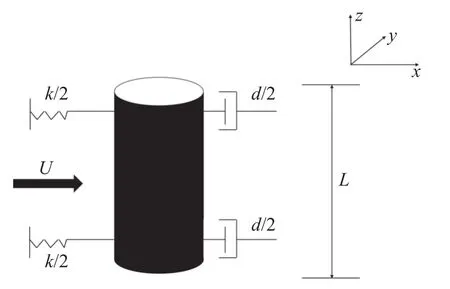
图3 Iwan-Blevins 模型示意
Iwan-Blevins 模型有以下基本假设:
1)在尾流相邻以外的流场为逼近于非黏性的流动;
2)存有一个脱落频率明确并且充分成型的旋涡;
3)仅在圆柱体的附面层产生旋涡现象,并且该旋涡是先均匀增加,直到达到强度最大,再向下游动;
4)流动是二维的;
5)圆柱所受到的力仅与流体相对于圆柱的平均流速和平均加速度有关。
该模型不仅适用结构处于均匀流时的涡激振动分析,也适合于结构处在非均匀流中的涡激振动响应预测。它应用范围较广,用于计算雷诺数[22]在103~105且圆柱体是弹性结构的响应。此外,对于刚性和非均匀的管道也同样适用[23],其数学表达式为
式中:K为斯特劳哈尔数相关的参数,α1、α2为与K相比的2 个很小的无量纲常数,α3、α4为无量纲常数,X为隐含流体变量,y为变量,α0为比例常数,ωn为圆柱体的固有频率,ωs为漩涡脱落频率,εT为总的有效阻尼系数。
2 脐带缆数值模型建立
2.1 脐带缆的基本参数
本文借助OrcaFlex 软件来分析某脐带缆的VIV 特性,脐带缆主要参数如表1 所示。

表1 脐带缆的参数
2.2 海洋环境的基本参数
选取一年一遇、十年一遇和两百年一遇海况作为研究变量,相对应的海洋参数如表2 和表3所示。
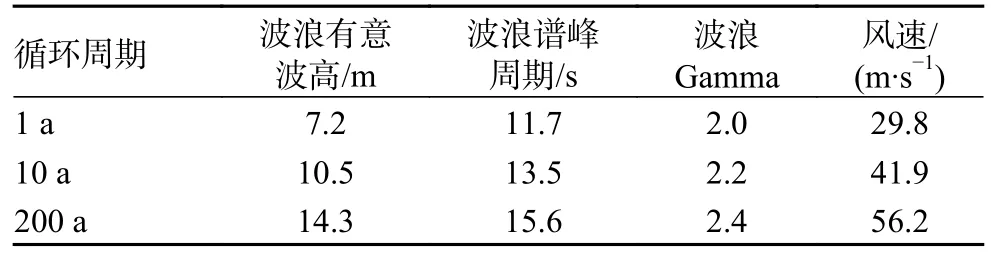
表2 风浪主极值
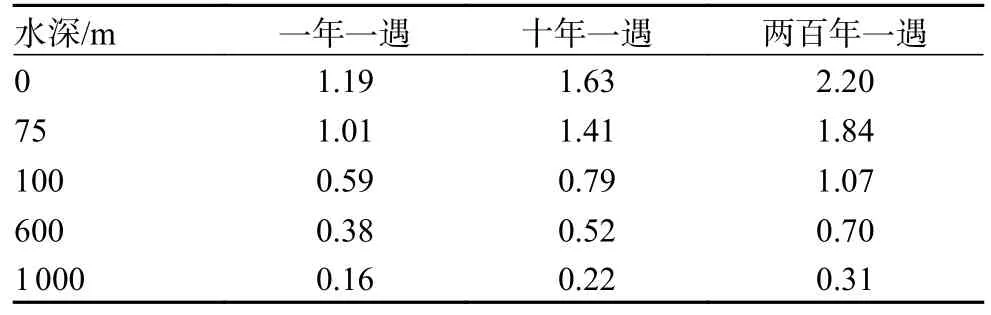
表3 海流极限流速 m/s
2.3 OrcaFlex 模型的建立
利用Orcaflex 软件建立的单根脐带缆模型如图4 所示,将图4 规定为脐带缆的主视图,其中以船体和脐带缆连接处为原点,向右为x轴正方向,向里为y轴正方向,向上为z轴正方向,脐带缆总长为1 370 m,水深设置为1 000 m,将表1~3 参数输入到整体线型水动力分析数值模型中,尾流振子模型选用Iwan-Blevins 模型,同时风浪和水流的方向为初始方向保留不变。数值模拟选取无铠装层和两铠装层2 种情况下的一年一遇、十年一遇和两百年一遇共6 种情况进行模拟分析,时间设为1 h。
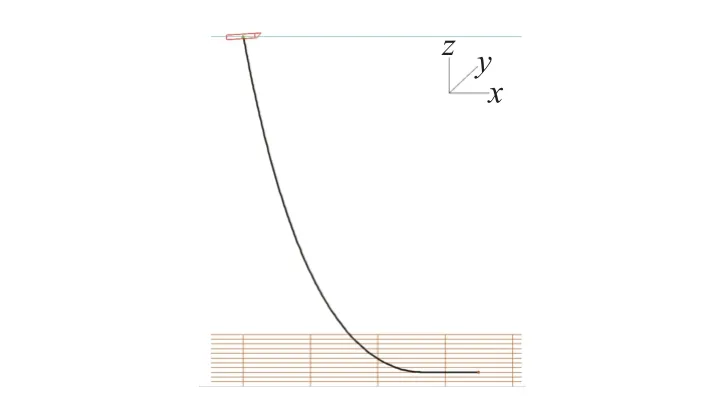
图4 Orcaflex 模型的建立
3 结果分析
3.1 脐带缆的振型分析
振型图可以很好地反映脐带缆的结构特性,包含各位置偏移量、弯曲程度以及变换情况等。因此,有必要研究脐带缆的振型图对整体结构的影响。
图5 是脐带缆一阶振型,图中的观察视图为左视图,在整个1 h 内所占的时间为79.432 s,可以很好地反映脐带缆所受VIV 时所呈现出的形态。图5 中脐带缆的位置偏移量由海面到海底先增大,增大到靠近海底上方到达最大值,接着靠近海底处再减小,这反映了该阶段脐带缆涡激振动在海底处的影响较大。
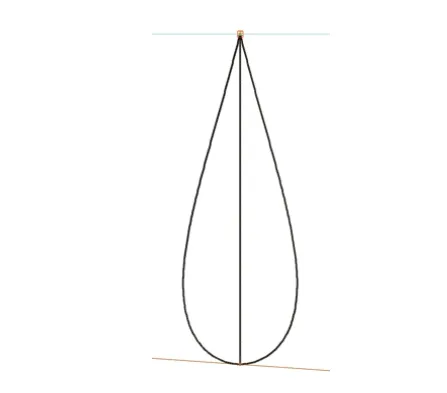
图5 脐带缆一阶振型
图6 是脐带缆二阶振型图,图中观察的视图为主视图,在整个1 h 内所占的时间为45.677 s,时长仅次于一阶振型图的时间,也可以很好地反映脐带缆所受VIV 影响时的形态。图6 中摆动偏移的上下两线型相重合产生的节点位置有3 处,分别是海面、海底和海中间处,可以看出脐带缆的偏移从海面的节点处往海中间节点处先增大再减小,接着从海中间节点往海底处的节点也同样是先增大再减小。根据振型图6,可以直接看出这个阶段的偏移影响较为明显的地方是靠近海面处和海底处。
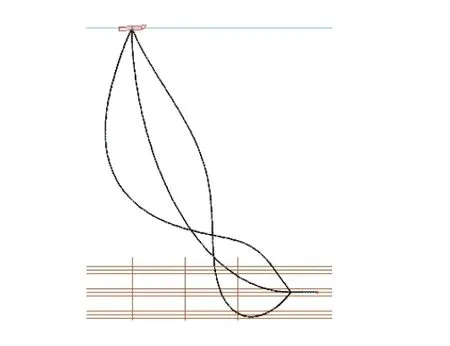
图6 脐带缆二阶振型
图7 是脐带缆的三阶振型图,图中的观察视图是左视图,在整个1 h 内所占的时间为40.036 s,时长仅次于一阶和二阶振型时间。偏移量从海面到海中间节点先增大再减小,再从海中间节点到海底也同样是先增大再减小,并且所受到的影响较大的位置同样也是靠近海面与海底。
图7 脐带缆三阶振型
图8 是脐带缆的四阶振型图,图中观察的视图为主视图,在整个1 h 内所占的时间为31.018 s,时长仅次于一到三阶振型时间。通过观察可看出,图8 中摆动偏移的上下两线型相重合产生的节点有5 处,海面、海底和海中间的有3 处,在图中偏移较大的位置是海面、海底与海中间处,说明这个阶段脐带缆在海面处、海底处和海中间处均受到一定的影响。
图8 脐带缆四阶振型
通过上述四阶振型图可以看出,对于脐带缆位置偏移影响较大还是海面处与海底处,同时海中间也有一定的影响,对于后续的五阶振型至多阶振型,其各阶段的时间所占比较小,在此就不一一赘述了。
3.2 铠装层数对VIV 的影响
对OrcaFlex 模拟仿真数据结果进行提取处理,提取了3 类数据结果,分别是VIV 的横向偏移量、脐带缆受到的有效张力最大值以及脐带缆的自身加速度大小,对这3 类数据结果研究对比可以很好地反映出脐带缆在不同条件下所受到VIV 的影响程度。
图9 为1 a 重现期的无铠装层和两铠装层的VIV 横向偏移量对比,表4 为不同脐带缆长度位置处1 a 重现期不同铠装层数VIV 横向偏移量具体数值。
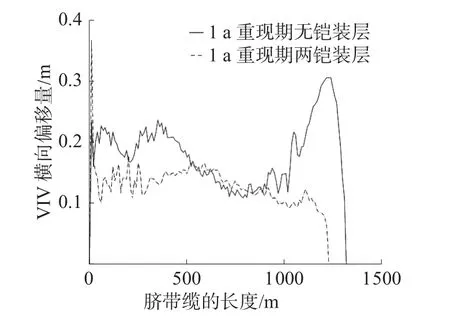
图9 1 a 重现期无铠装层和两铠装层VIV 横向偏移量对比
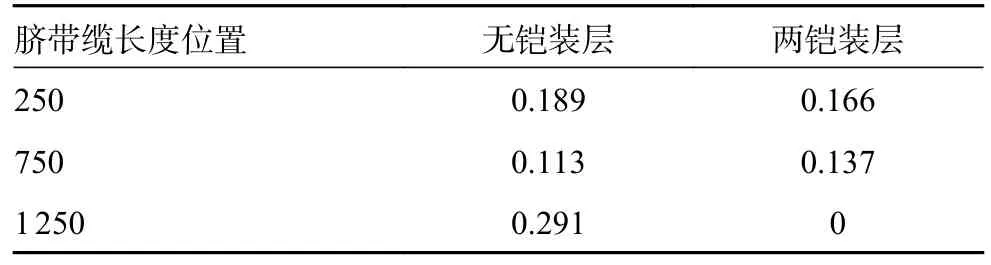
表4 1 a 年重现期无铠装层和两铠装层VIV 横向偏移量m
结合图9 表4,从整体分析无铠装层脐带缆,可看出该海况下的脐带缆在靠近海面与海底处的VIV 横向偏移量较大,其数值在脐带缆位置250m处和1250m处分别为0.189m和0.291m,均大于750 m 处的0.113 m,且在海面往海中间呈现一个波动较大但逐步下降的趋势,接着到海底再呈现一个较为平滑但是上升的趋势,最后在脐带缆末端回到0 值。在无铠装层的时候,VIV 的横向偏移量整体在靠近海底的时候更为剧烈,在海中间处较为缓和,在靠近海面处波动较大。铠装层数由无变成两层时,除海面处,靠近海面和海底处的VIV 横向偏移均有所缓和,说明铠装层数增加可以有效减小VIV 横向偏移量。
图10 为1 a 重现期时无铠装层脐带缆和两层铠装层的脐带缆有效最大值的对比图,可以看出,从海面到海底脐带缆受到的有效张力最大值逐步减小。就无铠装层脐带缆而言,海面到海底的有效张力最大值变化较为平缓。表5 为不同脐带缆长度位置处一年重现期不同铠装层数有效张力最大值。
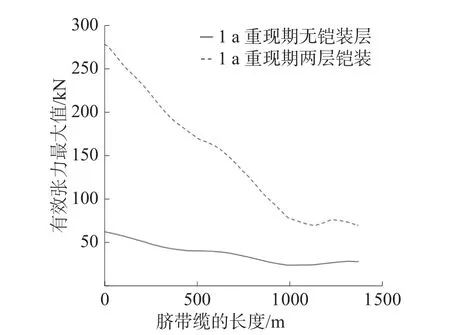
图10 1 a 重现期无铠装层和两铠装层脐带缆有效张力最大值对比
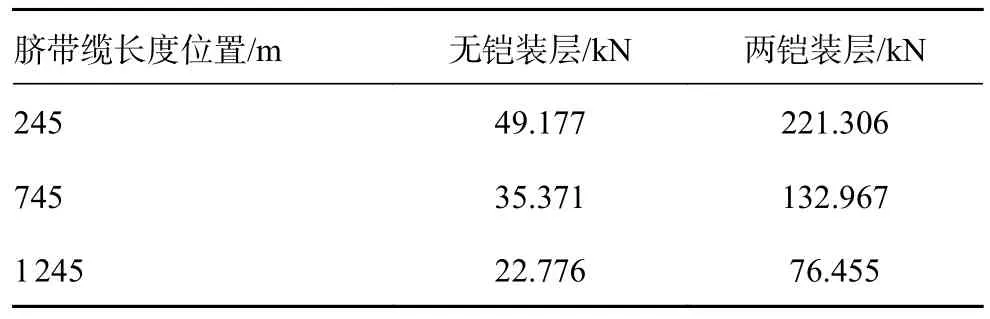
表5 1 a 重现期无铠装层和两铠装层有效张力最大值
由表5 可知,从245~1 245 m,无铠装层有效张力最大值变化是26.401 kN,而两铠装层有效张力最大值的变化则达到了144.851 kN,两铠装层的脐带缆从海面到海中间下部分,呈现一种类似于线性下降的趋势;从海中间下部分到海底,呈现一种较为平滑和缓慢波动的趋势。对比两脐带缆的曲线可以看出,两铠装层脐带缆的有效张力最大值明显大于无铠装层脐带缆的有效张力最大值。由前文可知,增加脐带缆铠装层数会同时导致有效张力最大值增加,其原因很大程度是铠装层数的增加导致单位长度的脐带缆重量增加,从而导致了有效张力最大值的增加,且增加后的有效张力最大值变化幅度也更为剧烈。因此铠装层数要适当的增加才能抵御涡激振动的影响。
图11 是1 a 重现期无铠装层和两铠装层脐带缆加速度数值对比。可以看出,无铠装层和两铠装层的加速度大小总体变化趋势从海面到海底逐步减小。表6 为不同脐带缆长度位置处加速度数值。
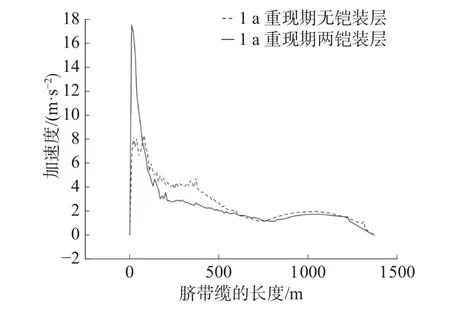
图11 1 a 重现期无铠装层和两铠装层加速度对比
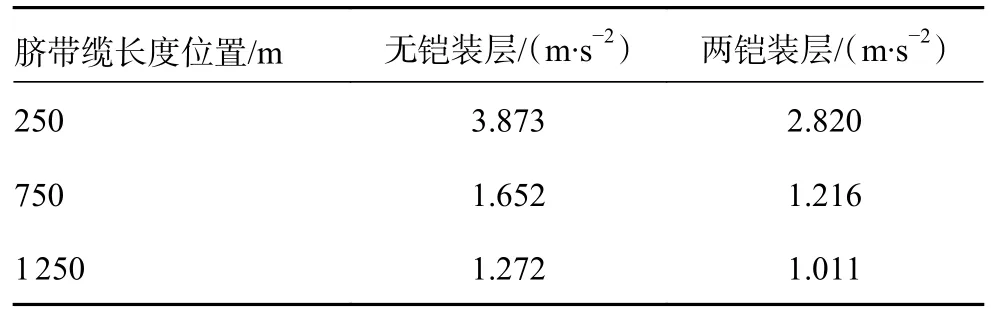
表6 1 a 重现期无铠装层和两铠装层加速度
脐带缆的加速度从其长度250 m 到750 m再到1 250 m 处,呈现减小的趋势。就无铠装层而言,脐带缆的加速度大小从海面到海中间处先波动下降,接着从海中间处到海底,脐带缆的加速度缓慢下降。对于两铠装层,加速度在靠近海面处最大,接着从海面到海中间是一个快速下降的过程,再从海中间到海底也是呈缓慢下降的趋势。对比2 种铠装层数的加速度曲线,随着铠装层数由无增至两层,靠近海面处的加速度有个突出的极值;加速度在海中间靠近海面处是一个减小的趋势;在靠近海底近似可以看成一条重合的曲线。这说明加速度在靠近海面处和海底处均没有得到有效缓解,甚至在海面处铠装层数的增加反而使得加速度极值有所增加,而在海底处几乎没有影响。
3.3 重现期对VIV 的影响
图12 为不同重现期无铠装层脐带缆VIV 横向偏移量对比。可以看出,就1 a 重现期的脐带缆而言,整体在从海面靠近海中间处,脐带缆的VIV 横向偏移量由缓慢波动轻微上升的趋势到缓慢波动下降的趋势,接着从海中间到海底呈现出剧烈上升到缓慢下降再剧烈下降的趋势,且上升后的数值远远大于靠近海面处。无铠装层脐带缆由于单位质量较轻,所以脐带缆所呈现出的VIV 横向偏移量差距较为明显。不同脐带缆长度位置不同重现期无铠装层VIV 横向偏移量数值如表7 所示。
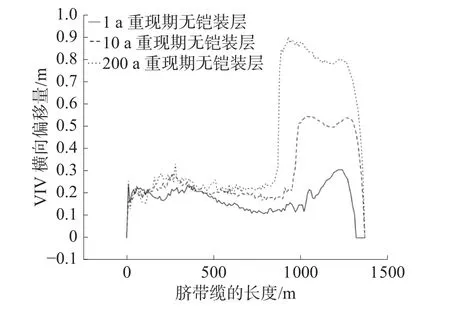
图12 不同重现期无铠装层VIV 横向偏移量对比
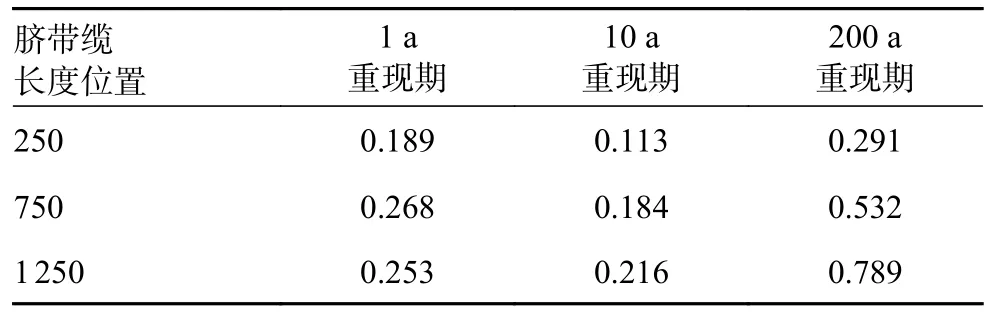
表7 不同重现期无铠装层VIV 横向偏移量 m
在脐带缆1 250 m 处的位置差距明显增大,其中200 a 重现期无铠装层较10 a 重现期无铠装层的VIV 横向偏移量数值差距较达到了0.257 m。随着重现期增至10 a 和200 a,靠近海面处的VIV横向偏移量所受影响不大;但是在靠近海底处,VIV 的横向偏移量明显增大,这进一步反应了脐带缆在海底处所受到VIV 影响程度较大。
图13 为不同重现期无铠装层脐带缆有效张力最大值数值对比,就1 a 重现期而言,从海面到海中间上方,脐带缆有效张力最大值,呈现出较为光滑且快速下降的趋势。不同脐带缆长度位置处不同重现期无铠装层的有效张力最大值如表8 所示。
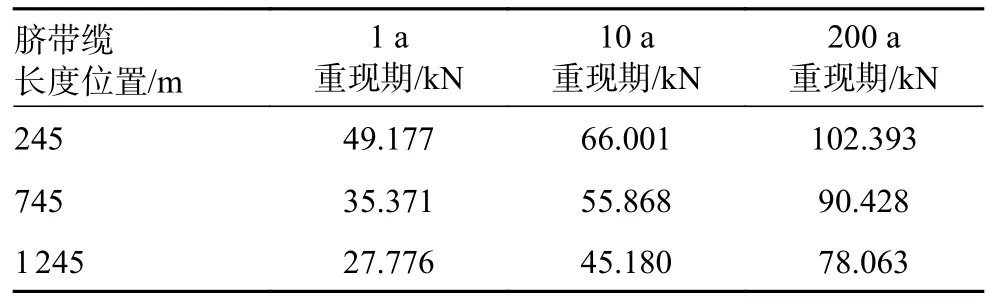
表8 不同重现期无铠装层有效张力最大值
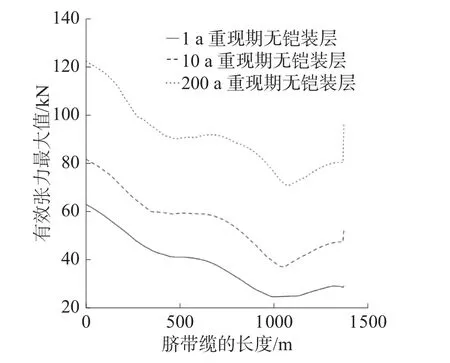
图13 不同重现期无铠装层有效张力最大值对比
如表8 所示,脐带缆位置245 m 处的有效张力最大值要大于位置745 m 和1 450 m 处,海中间上方减小更为快速。从海面中间上方到海面中间下方,呈现出下降趋势较为缓慢且平滑的趋势,接着从海中间下方到海底呈现出平滑缓慢上升的趋势,且随着重现期从1 a 增至10 a 和200 a,各部分的有效张力最大值均有所增加,这说明了海面处所受到的VIV 影响更为明显,且随着重现期的增加整体的影响都有所增大。
图14 为不同重现期无铠装层脐带缆加速度对比图。可以看出,对于1 a 重现期的脐带缆,其最大值在靠近海面处,从海面到海底处,脐带缆的加速度先是波动,接着较为快速下降,再是缓慢下降,最后平缓下降。
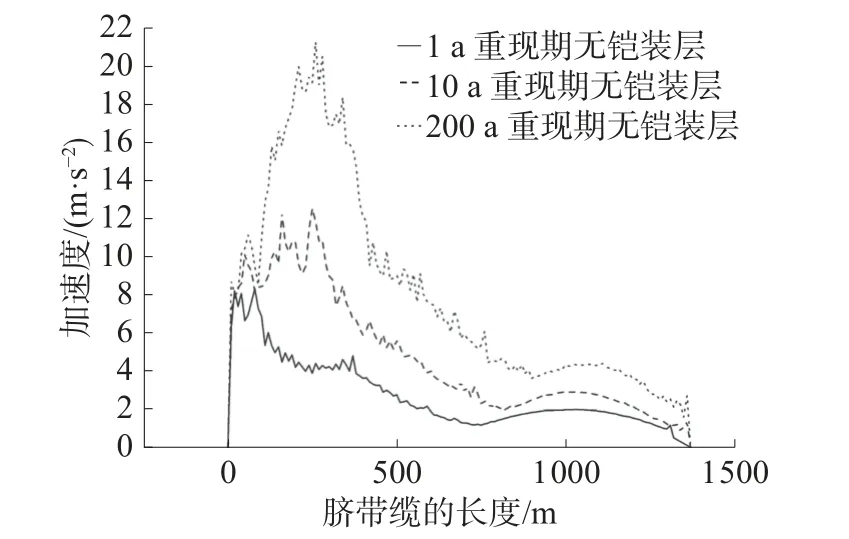
图14 不同重现期无铠装层加速度对比
表9 为不同脐带缆长度位置不同重现期无铠装层加速度数值。在脐带缆位置250 m 处的对应的加速度大小分别为3.873、12.528 和19.142 m/s2,明显大于脐带缆位置750 m 处和1 250 m 处的加速度大小。随着重现期增至10 a 和200 a,整体变化趋势和1 a 重现期类似,但是加速度的数值均有所增加,这说明重现期的增加使得脐带缆所受到的VIV 影响更为明显。
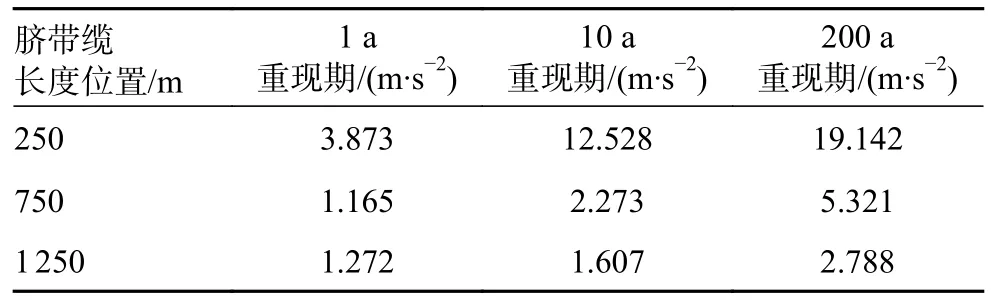
表9 不同重现期无铠装层加速度数值
4 结论
本文工作以脐带缆作为研究对象,运用OrcaFlex 建立悬链线型的仿真模型,对脐带缆所受VIV 横向偏移量、有效张力最大值和加速度进行了系统分析,在此基础上研究了脐带缆铠装层数和重现期对脐带缆VIV 特性的影响,得到的主要结论如下:
1)对于脐带缆的整体分析可知,脐带缆在海底和海面处所受到VIV 影响最大,在整体上都有不同程度的波动,且从海面到海底处会有先下降后上升的趋势。
2)针对铠装层数对脐带缆的影响分析可知,铠装层数的增加,会同时导致脐带缆单位长度的质量增加,虽然对抵御VIV 的横向偏移量有所作用,但是对于脐带缆所受的有效张力是增加的,因此在选取时,应综合考虑,平衡两者之间的关系,适当的增加铠装层数可以抵御VIV 对脐带缆的影响。
3)针对于重现期对脐带缆的影响而言,随着重现期的年限数增大,脐带缆所受到的VIV 影响明显呈增加趋势。
针对上述的结论提出可供参考的有关脐带缆结构设计相应的改进措施:
1)考虑到海面和海底处脐带缆所受的VIV 影响更为明显,可以采取选取局部保护的措施,例如选取更为优质的材料,增加一些保护套等;
2)对于使用周期较长的脐带缆,需要考虑较长的重现期年数,在综合考虑得当的情况下,可以适当增加脐带缆的铠装层数。
