基于改进K-means聚类的惯性行人导航零速检测算法*
2022-03-24戴洪德张笑宇刘郭家豪郑百东吕
戴洪德张笑宇刘 伟*郭家豪郑百东吕 游
(1.海军航空大学航空基础学院,山东 烟台 264001;2.海军航空大学岸防兵学院,山东 烟台 264001;3.海军航空大学教练机模拟训练中心,葫芦岛 125000)
微机电系统(MEMS)的兴起极大地促进了MEMS惯性传感器在导航领域应用的发展。基于MEMS惯性器件的惯性导航系统的发展有效弥补了卫星导航系统在室内、井下和隧道等特殊环境下无法导航的缺陷,成为了导航系统领域重要的研究方向。
为了克服行人惯性导航系统的误差累积问题,Elwell等人根据行人运动时脚相对地面周期性静止的特点,提出了一种以零速作为观测量进行周期性误差修正的算法,即零速修正(zero velocity update,ZUPT)算法[1-2]。零速修正算法的提出为基于惯性的行人导航理论提供了新的研究思路,并逐渐成为惯性行人导航系统的主流研究方向。获取行人步态周期内的零速区间是进行零速修正的前提。根据零速区间的步态特征,国内外学者提出了出了一系列的零速检测算法,如加速度移动方差检测算法(acceleration moving variance detector,)[3-4],加速度幅值检测算法(acceleration magnitude detector)[3,5],角速率能量检测算法(angular rate energy detector)[6-7]等,作者课题组也提出了一种基于伪标准差和N-P准则的行人导航零速检测算法[8]。由于上述几种算法采用固定阈值进行零速检测,因此只能对单一的运动状态进行零速检测,适应性差。为了解决零速检测算法适应性差的问题,国内外学者提出了出了一系列具有自适应特性的零速检测算法[9-11],Isaac Skog提出了一种基于贝叶斯的自适应阈值零速检测算法[12](BAT),孙伟也提出了步态特征提取的K均值聚类自适应判别算法[13](KCA)。
Isaac Skog提出的基于贝叶斯的自适应阈值零速区间检测算法(BAT)虽然利用设定阈值的衰减规律在一定程度上实现了在多种运动状态下的零速检测,但是设定的阈值变化规律在遇到预期之外的运动状态时,很难确保零速检测的精度。孙伟提出的步态特征提取的K均值聚类自适应判别算法(KCA)通过K-means算法对每个步态周期内的所有数据点进行聚类,有效地减小了阈值对零速检测精度的影响,具有良好的适应性,但是还存在Kmeans算法聚类点数过多,计算量大,导致计算时间过长的问题。因此,本论文提出了一种基于改进Kmeans聚类的零速检测算法(IKC),通过K-means聚类算法获取聚类中心点。然后利用聚类中心点实现对零速区间的检测。相比于步态特征提取的K均值聚类自适应判别算法(KCA),本文提出的IKC算法根据同一运动状态下聚类中心点相对稳定的特点,依据数据点与中心点距离差异划分零速区间,简化了聚类流程。该算法有效减小了计算量,缩短了计算时间。本文还将Isaac Skog提出的基于贝叶斯的自适应阈值零速检测算法(BAT)、孙伟提出的步态特征提取的K均值聚类自适应判别算法(KCA)与本文提出的基于改进K-means聚类的零速检测算法(IKC)进行对比分析。理论分析和实际行人导航实验,都验证了本文所提方法的有效性。
1 K-means聚类自适应判别算法
1.1 零速区间步态特征
通常将行走过程中行人从一侧脚跟着地开始,经两只脚步态交替变换,到该侧脚跟再次着地时所经历的过程定义为一个完整的步态周期。其中,当一条腿承重时,其脚底与地面完全接触,此时,将脚与地面完全接触的时间段称为零速区间。零速区间如图1所示[14]。

图1 步态周期
当行人处于零速区间时,其步态特征为:足部的角速度及水平加速度值近似为零,竖直方向的加速度值近似为重力加速度。
本文研究的存在多种运动状态变换的行人运动均是在平地上进行,已有研究证明在平地上运动陀螺仪提供的角速度数据足以完成零速检测任务[15]。因此,在本文后续的实验中只采用了来自陀螺仪提供的角速度数据进行零速检测。
1.2 K-means聚类算法
聚类是一种发现数据内在结构的无监督学习技术,应用聚类算法对行人行走时的运动状态进行划分,可以在不依赖阈值的情况下实现零速检测。
聚类技术包含划分法、层次法、基于密度的方法、基于网格的方法和基于模型的方法等多种算法。这些方法各有优缺点。其中,K-means聚类方法具有简洁高效的优点,也存在需要预先设定K值的缺点。
K-means聚类的具体流程是:先随机选取K个数据点作为初始的聚类中心。然后计算每个数据点与各个聚类中心之间的距离,把每个数据点分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类,称为簇。一旦全部对象都被分配了,每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是以下任何一个:①没有(或最小数目)对象被重新分配给不同的聚类。②没有(或最小数目)聚类中心再发生变化。③误差平方和局部最小。
可以看出,在K-means聚类方法中只需要设定K值就可以实现数据点的聚类,相比于其他聚类方法的条件更加容易满足。
KCA算法将零速检测转化为一种划分零速区间与非零速区间的二分类问题,所以将K值明确取为2。K-means聚类方法如图2所示。

图2 K-means聚类示意图
1.3 KCA算法
为了解决固定阈值无法对步态特征进行自适应判别的问题,孙伟提出了步态特征提取的K均值聚类自适应判别算法[13](KCA)。
此算法通过初步检测将步态周期分为初始动态与初始静态,然后分别进行K-means聚类,分别选取初始动态与初始静态持续时间最长的动态与静态部分作为真动态与真静态,其余部分作为假动态与假静态。
然后,根据Dunn指数作为聚类结果的指标,将真静态与真动态进行对比。Dunn指数的具体公式如下:

式中:dmin(C i,C j)=minx i∈c i,x j∈c jdist(x i,x j);diam(Cl)=max1≤i≤j≤|C|dist(x i,x j)。dmin(C i,C j)反映簇与簇最近样本间的距离;diam(Cl)反映簇内样本间的最远距离;dist(xi,x j)表示样本之间的距离。由于样本为各状态持续时间长度,因此采用绝对值距离。
若真静态的Dunn指数较大,则表明静态聚类效果优于动态聚类,应按静态聚类结果将假静态纠正为动态;反之,则将假动态纠正为静态。
KCA算法在实验中表现出较好的实验结果,解算得到的位置相对误差优于2%[13]。其具体流程图如图3所示。

图3 KCA算法
2 改进K-means聚类零速检测算法
KCA算法虽然有效解决了零速检测结果过于依赖阈值的问题,但是无论是在计算时间还是检测精度上仍具有较大的提升空间。因此,本文根据K-means聚类算法的特点,对其进行了改进,在缩短计算时间的同时提高了导航精度。
2.1 类数目K值
本文通过对角速度数据的分析发现在非零速区间陀螺仪输出的角速度变化范围大,存在正负之分,而在零速区间内陀螺仪输出的角速度理论上为零,取K值为2易将部分非零速区间划分到零速区间。
在KCA算法中,为了避免出现上述问题,会先通过其他零速检测方法进行初始检测。这虽然在一定程度上确保了聚类精度,但是多次的零速检测导致KCA算法计算量过大,不利于实时检测。
因此,本文根据角速度的数据变化规律在将运动划分为零速区间与非零速区间的基础上又将非零速区间划分为正负两个部分,将K值取为3,旨在通过划分三个部分减少引入到零速区间的误差。陀螺仪输出如图4所示。

图4 陀螺仪输出
2.2 改进K-means聚类
KCA算法对步态周期内的每个数据点都进行了K-means聚类,目的是通过这种方法摆脱零速检测对阈值选取的依赖。但是由于整个运动过程中获取的数据点过多,产生了计算量过大,实时性不高的问题。
针对上述问题,本文提出了一种改进的Kmeans聚类算法。该算法根据同一运动状态下,聚类中心点相对稳定的特点,依靠聚类中心点进行零速检测。其具体做法是首先对处在同一运动状态下的部分运动数据进行K-means聚类获得聚类中心点。然后,依据聚类中心点对同一运动状态下的运动进行零速检测,这里零速检测的数据包括在上一步为获取聚类中心点所使用的数据。
当某一数据点满足如下条件时:

则判断该数据点属于零速区间,否则,该数据点属于非零速区间。其中,D0是数据点到零速区间聚类中心点的距离,D1和D2为数据点到非零速区间正负两个部分的聚类中心点的距离,α和β则是对应的比例系数。
本文根据先验信息确定了α和β的取值范围。首先根据图像与数据特点区分出每个步态周期的零速区间与非零速区间的数据点;然后计算出这些数据点的中心点;计算数据点到零速区间中心点的距离与到非零速区间中心点距离的比值,即可求出比例系数的取值范围。

式中:α和β则是第k个步态周期对应的比例系数;D0k是第k个步态周期内,零速区间数据点到零速区间聚类中心点的距离;D1k和D2k为第k个步态周期内,非零速区间正负两个部分数据点到对应部分的聚类中心点的距离。
改进K-means分类结果如图5所示。

图5 改进K-means聚类示意图
考虑到零速区间内部点的紧密程度要远高于零速区间数据点与非零速区间数据点的紧密程度。因此,零速区间内部数据点到零速区间聚类中心的距离远小于零速区间内部数据点到非零速区间聚类中心的距离。据此,本文设计了α和β作为比例系数体现不同区间内点的紧密程度。
2.3 验证
由于K-means聚类算法是对点的数据进行聚类,且陀螺仪输出的角速度数据在非零速区间变化时存在零角速度的数据点,因此,易将非零速区间内零角速度的数据点误判为零速区间的数据点。具体表现在聚类结果不符合实际情况,短时间内检测得到的多个零速区间。
在KCA算法中,会将通过K-means聚类算法得到的多个零速区间中持续时间最长的作为真静态,然后通过Dunn指数与真动态进行比较。但是,由于零速区间内的数据点远比非零速区间内的数据点更密集,导致在大多数情况下,真静态更易被判断为好。
在IKC算法中,由于增设了比例系数,因此,只有将非零速区间内零角速度的数据点误判为零速区间的数据点时才会在短时间内检测得到的多个零速区间的情况,且错误的零速区间持续时间远小于实际零速区间的持续时间。
因此,本文对得到的零速区间进行检验,当满足如下条件时:

则判断该零速区间有效,否则该零速区间无效且变更为非零速区间。其中,Qt为零速区间的结束时对应的数据点编号,Q t-1为零速区间的开始时对应的数据点编号;f为采样频率;T1为设定的零速区间持续时间最小值。
2.4 运动状态检测
由于改进的K-means聚类算法是在同一运动状态下进行的,因此,当运动状态发生变化时,需要重新获取聚类中心点。
为了判断行人运动状态是否发生变化,本文根据行人的运动特点,选取行人在非零速区间时由抬脚运动变为落脚运动的时刻作为统一的判断运动状态的时刻。当行人处于该时刻时,行人的速度即为水平方向上的速度,计算行人的速度,通过比较相邻两个步态周期行人速度的大小判断运动状态是否发生变化。当满足如下条件时:

判断运动状态没有改变,若不满足条件则认为运动状态发生了改变。
其中,a z表示加速度计z轴数据,V k表示第k个步态周期行人的速度,γ为设定的速度波动范围,γ越小运动状态检测的灵敏度越高,但是也会增加检测的计算量。
同时,为了防止运动状态逐步变化导致前后两次对比无法发现运动状态改变的情况,本文还在此基础上设定了固定的检测时间。当判断行人维持某一运动状态时间T超过时间T2时,则同样进行检测。
基于改进的K-means聚类零速检测算法的具体流程图如图6所示。

图6 基于改进K-means聚类的零速检测算法
相比于KCA算法,本文提出的IKC算法有效的减小了零速检测的计算量,具有更好的实时性;IKC算法通过比例系数,有效避免了K-means聚类产生的误差,提高了零速检测精度,并使得算法验证部分更加简洁,进一步缩短了计算时间。
3 实验验证
本文在实验过程中采用荷兰Xsens公司生产的Mti-G-710系列MEMS惯性传感器作为行人导航惯性元件,其内置了三个相互垂直的加速度计和陀螺仪,能够实时测量载体运动的加速度以及角速度。加速度计的量程为±50 m/s2,陀螺仪的量程为±450°/s,惯性传感器的工作频率设置200 Hz。惯性传感器如图7所示。

图7 Mti-G-710系列MEMS惯性传感器
本文中使用的所有实验数据,均是通过将该传感器固定在脚后跟处[14]进行相应的运动得到的。
3.1 K的取值
K的取值是影响本文提出的IKC算法结果的关键。本文提出的IKC算法并没有对全部数据进行K-means聚类,这在减小计算量的同时也导致算法缺少对整体数据情况的把控。因此,本文根据陀螺仪输出的角速度数据特点,设定K值为3,以此来增加改进K-means聚类算法对整体数据的把控。
由于在KCA算法中,比例系数固定为1,为了验证K的取值,本文在设定IKC算法的比例系数均为1,其他实验流程相同的前提下,分别对同一组数据进行取K值为2和3基于改进K-means聚类的零速检测实验以及KCA算法实验。其结果如图8、图9与图10所示。

图8 KCA算法零速检测

图9 IKC(K=2)算法零速检测

图10 IKC(K=3)算法零速检测
图8至图10中,纵坐标为陀螺仪的输出角速度数据以及零速检测的结果Q。当Q为零时,表示行人处于非零速区间,Q为非零时,表示行人处于零速区间。横坐标为运动数据的时间点。
将图9与图10中的零速检测结果分别与图8的进行对比,结合图中角速度数据的波动情况,可以发现当K=3时,本文提出的IKC算法检测得到的零速区间更加符合实际情况,验证了本文提出算法取K值为3的合理性。
3.2 比例系数
结合陀螺仪输出的角速度数据可以看出,在图9与图10中,改进的K-means聚类算法得到的零速区间持续时间还是要略长于实际零速区间的持续时间。这是由于零速区间内的数据点相比于非零速区间内的数据点更加紧密,而无论是K-means聚类还是上述的改进的K-means聚类只考虑了各个数据点到中心点的距离,而缺乏对数据点实际分布情况的考虑。因此,本文在改进的K-means聚类的基础上增加了比例系数,旨在通过零速区间与非零速区间数据点分布密度的差异进一步提高获得的零速区间的精度。
本文根据式(2)和式(3),可以确定最佳比例系数的取值范围。为了对比例系数的作用进行分析,本文在图10比例系数为1的基础上,又分别取比例系数为0.5和0.05进行实验,其中0.05属于最佳比例系数的取值范围,其结果如图11与图12所示。

图11 IKC(0.5)算法零速检测

图12 IKC(0.05)算法零速检测
结合图11与图12的辅助虚线可以看出,比例系数为0.05时的IKC算法的零速检测效果要明显优于比例系数为0.5和1时的IKC算法的零速检测效果。因此,证明可以通过设置比例系数来提高IKC算法零速检测的灵敏度,进而提高零速检测精度,从而有利于提高导航精度。
为了进一步验证比例系数对导航精度的验证,本文通过卡尔曼滤波算法对上述三种不同比例系数得到的零速区间进行位置解算。
在本文路径实验中采用的所有实验数据,其运动轨迹均为矩形,每次矩形运动,会有多次运动状态变化,并要求在结束运动时,尽可能确保安装有传感器的脚回到运动初始点。位置解算得到的运动路径图像如图13所示。图13中,点线代表比例系数为0.05时的IKC算法,点划线代表比例系数为0.5时的IKC算法,虚线代表比例系数为1时的IKC算法,黑线代表行人实际的运动路径。从图13中可以看出,点线与点划线的轨迹相比于虚线更符合实际运动轨迹,进一步证明比例系数能有效提高导航精度。

图13 实验路径对比
3.3 计算时间对比
本文提出的IKC算法只在运动状态发生变化时才进行完整的K-means聚类,在同一运动状态下的零速检测都是依靠K-means聚类获得的中心点实现的,而KCA算法对整个运动过程中的所有数据点进行了完整的K-means聚类。因此,理论上本文提出的基于改进K-means聚类的零速检测算法的计算量更小,计算时间会更短,更符合实时导航的需求。
为了验证本文提出的IKC算法的计算速度优于KCA算法,本文在同一电脑上,取了五组运动数据,分别采用IKC算法、BAT算法以及KCA算法三种算法进行零速检测,记录算法运行时间。
T1表示IKC算法的计算时间;T2表示BAT算法的计算时间;T3表示KCA算法的计算时间。实验结果如表1。

表1 运行时间结果 单位:s
从表1中可以看出,本文提出的IKC算法有效减小了计算量,在计算时间上略优于BAT算法,而相比于KCA算法则是显著地减小了计算时间。
3.4 导航位置精度对比
为了验证本文提出的IKC算法对行人导航精度的影响,本文对同一运动分别采用IKC算法和KCA算法进行零速检测,并采用基于Kalman滤波的零速修正算法进行位置解算,最终实现导航精度对比实验。
由于BAT算法无法适应运动状态变化导致的数据的剧烈波动,因此,在位置精度对比中未采用BAT算法进行零速检测。通过IKC算法和KCA算法得到的运动路径图像如图14所示。图14中,虚线代表采用了IKC算法得到的运动路径,点划线代表采用了KCA得到的运动路径,黑线代表行人实际的运动路径。从图14中可以看出,IKC相比于KCA算法导航精度更高。

图14 实验的路径对比
为了定量对比IKC算法和KCA算法的导航精度,本文取相应的转折点及终点,作为实际行走轨迹参考点在解算轨迹中的对应点。对应点与参考点的位置误差定义为:

式中:r d表示对应点位置,r c表示参考点位置。
分别计算四个对应点与四个参考点的位置误差,将四个位置误差取平均值,作为解算轨迹与实际轨迹的导航轨迹误差平均值;对四个位置误差求标准差,作为解算轨迹与实际轨迹的导航轨迹误差标准差,计算方法为:
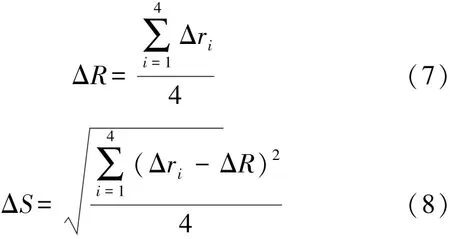
通过导航轨迹误差平均值以及标准差两个定量指标,即可量化IKC算法和KCA算法解算轨迹与实际轨迹的接近程度,从而评估IKC算法和KCA算法导航的准确性和稳定性。
由于矩形实验中涉及的行走轨迹为标准的矩形,解算得到的轨迹也较为接近矩形,因此可以通过上述四个参考点的位置误差平均值以及标准差来描述整个轨迹的导航误差,对于其他较为复杂的行走路径,则应该选择轨迹中多个具有代表性的点来描述导航轨迹误差。
从表2中的计算结果可以发现,在同一运动过程中,IKC算法具有更小的导航轨迹误差平均值ΔR,平均仅为0.57 m,只占总路程的1.14%,相对KCA算法减小了0.97%,表明IKC算法导航的精度更高,验证了IKC算法提高了零速检测的准确性。

表2 三种算法位置误差与导航轨迹误差
4 结论
本文提出的基于改进K-means聚类的零速检测算法在解决零速检测自适应问题的同时,有效减小了计算量,缩短了计算时间。相比于步态特征提取的K均值聚类自适应判别算法以及基于贝叶斯的自适应阈值零速检测算法,IKC算法更能适应在变速情况下的零速检测。
