基于K-近邻域搜索的遗传算法求解旅行商问题
2022-03-24徐伟华魏传祥张根瑞赵彩梅
徐伟华,魏传祥,张根瑞,赵彩梅,熊 坚
(昆明理工大学 交通工程学院,云南 昆明 650500)
0 引 言
旅行商问题(Traveling Salesman Problem,TSP)是多种组合优化问题的集中概括和基本形式,它在物流配送[1]、车辆路径优化[2]和生产调度等领域都有广泛应用.由Holland首次提出的遗传算法(Genetic Algorithm, GA)是一种启发式全局搜索算法,适用于处理离散问题和非线性问题.针对GA存在收敛速度慢、局部搜索能力差和容易早熟等不足,为提高GA求解TSP问题的性能,国内外研究者进行了诸多探索.Chang等[3]通过注入人工染色体的方法保持和提高种群多样性,防止算法陷入局部最优;Chang等[4]利用GA和蚁群算法构成的混合算法求解TSP问题;Victer Paul等[5]采用基于有序距离向量的种群初始化技术以提高种群的多样性;Wang[6]成功运用两种局部优化算子加强GA的局部搜索能力;Rafsanjani等[7]在GA中引入局部搜索算法并采用系数控制机制以弥补GA局部搜索能力较弱的不足;Hassanat等[8]采用基于线性回归分析的种群初始化方法;Riazi[9]在GA中引入双染色体方法,旨在加快算法的收敛速度;Hassanat等[10]研究了GA交叉和变异概率的动态控制策略;Kaabi等[11]采用基于最近邻的贪婪式种群初始化方法;Arram等[12]提出了多父级顺序交叉算子(Multi-Parent Order Crossover, MPOX),遗传算法求解质量有所提高;Paul等[13]为提高种群多样性和遗传算法的收敛速度,设计了基于有序距离向量的交叉算子以提高算法收敛速度;Mirzaie[14]将模因算法应用于GA的变异操作.
综上所述,以往研究的特点如下:(1)依靠种群播种技术和注入人工染色体的方法提高种群多样性;(2)引入其他智能算法弥补GA存在的不足;(3)通过设置参数自适应调节机制,提高算法收敛速度和求解精度;(4)设计新型交叉算子提高GA性能.与上述研究不同,本研究将通过分析TSP的特性,在变异操作中减少无效操作的同时从变异距离中获取启发式信息,提高变异操作的有效性和效率.此外,还通过改进选择模式,确保种群多样性不随种群的进化而逐代降低,防止算法早熟收敛.
1 问题的描述
基于图论可将TSP问题定义为:已知赋权无向完全图G(V,E),V是由n(n为正整数)个不同顶点所构成的顶点集V={v1,v2,…,vn},E是由V中的顶点两两连接而组成的边集E={(vi,vj)|vi,vj∈V},w(vi,vj)表示边(vi,vj)的距离.TSP问题就是要从G(V,E)中找到哈密顿回路X={x1,x2,…,xn},满足目标函数:
(1)
2 改进遗传算法
2.1 编码与种群初始化
GA把问题的可行解视为生物种群中的个体(染色体),通过编码将可行解转化为计算机可以处理的数据结构.本研究采用整数编码方式,一个完全排列的整数序列即为一条染色体.当TSP问题的可行解以染色体形式存在时会有多种等效情况,染色体中基因所代表顶点的相对顺序与哈密顿回路保持一致的染色体都等效,本文将这一特点称为染色体的“多态性”.为提高初始种群质量,借鉴贪婪算法的思想进行种群初始化.产生初始种群的基本步骤:
step1:从顶点集V中随机选择一个顶点作为染色体的首位基因;
step2:逐个从顶点集V中选择距离上一次加入染色体的顶点最近的顶点作为下一位基因,直到所有顶点被加入染色体且保证每条染色体中不存在重复顶点;
step3:重复N(N为正整数)次step1和step2则可生成初始种群,N即为种群规模.
2.2 变异操作

K-近邻域定义为:在给定的距离度量w中,对于包含n个顶点V={v1,v2,…,vn}的TSP问题,顶点vi(1≤i≤n)的K-近邻域是距离顶点vi最近的k个顶点的集合,记为Nk(vi)={c1,c2,…,ck},k(1≤k≤n)代表近邻域范围大小.用K-近邻度Pk(vi,cs)衡量顶点vi与其K-近邻域Nk(vi)中顶点cs(1≤s≤k)间远近程度:
(2)
此外,为提高算法的局部搜索能力,利用TSP问题中顶点间的距离信息,通过计算和比较变异距离差,选择合适的变异位置以提高算法的局部搜索能力.结合上述分析,设计了启发式移位算子(Heuristic Move Operator,HMO)和启发式逆序算子(Heuristic Reverse Operator,HRO).
2.2.1 启发式移位算子原理
step1:按变异概率选择个体X=(x1,x2,…,xn);
step2:从X中随机选择顶点xm(1≤m≤n),按公式(5)从Nk(xm)中选择近邻顶点xd.具体方法如下:先用公式(3)计算Nk(xm)中所有顶点被选概率p(cs),再用公式(4)分别计算Nk(xm)中前s个顶点的被选累计概率ps,最后生成一个随机数r∈[0,1],按公式(5)选择近邻点xd.如果xd==xm-1或xd==xm+1,返回step1;
相关计算公式如下:
(3)
(4)
(5)
step3:计算染色体移位变异后路径距离的变化值Δλ1和Δλ2:
Δλ1=(w(xd-1,xm)+w(xd,xm)+w(xm-1,xm+1))-(w(xm-1,xm)+w(xm,xm+1)+w(xd-1,xd))
(6)
Δλ2=(w(xd,xm)+w(xd+1,xm)+w(xm-1,xm+1))-(w(xm-1,xm)+w(xm,xm+1)+w(xd,xd+1))
(7)
Δλ1、Δλ2计算原理如图1所示.

(a)Δλ1计算原理 (b)Δλ2计算原理
step4:如果Δλ1≤Δλ2,将xm移动到xd-1和xd之间,否则将xm移动到xd和xd+1之间,如图2所示.

图2 染色体移位变异示意图
2.2.2 启发式逆序算子原理
step1:按变异概率选择个体X=(x1,x2,…,xn);
step2:从X中随机选择顶点xm,同上采用公式(5)从xm的K-近邻域Nk(xm)中选择一个近邻顶点xd;
step3:计算染色体逆序变异后距离的变化值Δλ3、Δλ4、Δλ5和Δλ6:
Δλ3=(w(xm-1,xd-1)+w(xm,xd))-(w(xm-1,xm)+w(xd-1,xd))
(8)
Δλ4=(w(xm-1,xd)+w(xm,xd+1))-(w(xm-1,xm)+w(xd,xd+1))
(9)
Δλ5=(w(xm,xd-1)+w(xm+1,xd))-(w(xm,xm+1)+w(xd-1,xd))
(10)
Δλ6=(w(xm,xd)+w(xm+1,xd+1))-(w(xm,xm+1)+w(xd,xd+1))
(11)
Δλ3~Δλ6的计算原理如图3所示:

图3 逆序变异距离计算原理图
step4:由于染色体具有“多态性”,因此xm和xd在染色体中的相对位置关系可能会有m
case0:Δλ3≥0且Δλ4≥0且Δλ5≥0且Δλ6≥0,不进行任何逆序操作;case1:d

图4 染色体逆序变异示意图
2.3 交叉操作
交叉操作是产生优质新个体的重要途径,能直接影响GA的求解精度和效率.多父级顺序交叉算子MPOX[12]是在双亲顺序交叉算子(Order Crossover, OX)的基础上发展而来,它可产生无重复个体且合法的后代.相比于传统的OX,应用MPOX的GA求解效率更高,因此本研究将采用MPOX进行变异操作.
2.4 适应度评价与选择
个体的评价和选择方式对种群多样性发展有重要影响.传统GA采用的轮盘赌法、锦标赛法等可实现优势个体的积累,然而随着种群的进化以及优势个体不断的积累,种群的多样性逐渐降低,不利于全局寻优.为更大程度地保留优质基因和保持种群的多样性,设计全精英选择法进行个体选择.全精英选择法是基于适应度值大小的选择方法,故采用路径总距离作为适应度值.全精英选择法的基本步骤:
step1:将交叉和变异产生的新个体与父代种群合并;
step2:将合并种群中的重复个体剔除;
step3:按照适应度值从小到大将所有个体排序并选择适应度最小的N个个体作为新种群.
2.5 改进遗传算法流程设计
综上,设计改进遗传算法(Improved Genetic Algorithm,IGA),如图5所示.

图5 改进遗传算法流程
3 实验与结果分析
实验在Intel Core i5-5200U 2.20 GHz处理器的计算机上进行,选用MATLAB 2018b作为编程软件和实验平台,对标准TSP问题实例进行仿真计算.设置种群的规模N=100,最大进化代数Gmax=5 000,交叉概率PC=0.8,启发式移位算子变异概率Pmm=0.1,启发式逆序算子变异概率Pmr=0.1,变异操作的K-近邻域搜索范围k=20.
3.1 局部搜索能力分析
图6是采用随机移位算子(Random Move Operator, RMO)和随机逆序算子(Random Reverse Operator, RRO)的GA求解Pcb442的路径图;图7是采用HMO、HRO的GA求解Pcb442的最优路径图.图6明显存在迂回路径,IGA求解效果更优,启发式变异算子可以有效提高算法局部优化能力.

图6 采用RMO和RRO的遗传算法求得Pcb442最优解

图7 采用HMO和HRO的遗传算法求得Pcb442最优解
3.2 种群多样性分析
种群多样性是指种群中所有个体之间的差异程度,有内在结构和外在特征上的差异.根据个体适应度值来定义种群多样性评价指标,已知包含N个个体的种群P={X1,X2,…,XN},种群适应度值F={f1,f2,…,fN}.包含N个个体的种群P的多样性评价指标[16]为:
(12)
在使用相同种群初始化方法(贪婪算法)和变异算子(HMO、HRO)情况下,分别采用轮盘赌选择法和完全精英选择法的GA求解Pcb442.图8展示了采用轮盘赌法的GA求解Pcb442种群进化过程中种群多样性随种群变化的情况,种群多样性呈现震荡下跌的趋势;图9是采用完全精英选择法的GA求解Pcb442过程中种群多样性的变化趋势,种群的多样性程度比较稳定且呈现微弱上升的趋势.通过比较图8和图9可以发现,相较于轮盘赌选择法,全精英选择法能更好地保持种群多样性.

图8 轮盘赌选择法
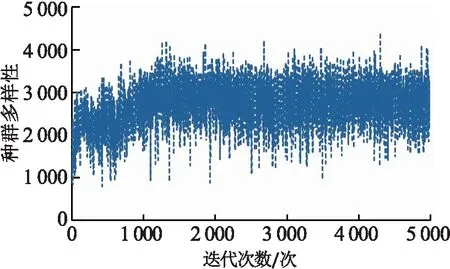
图9 全精英选择法
3.3 改进遗传算法整体性能分析
设计四组实验检验全精英选择法和启发式变异算子对算法性能的影响.Test1:贪婪算法种群初始化+MPOX交叉算子+随机变异算子+轮盘赌选择;Test2:贪婪算法种群初始化+MPOX交叉算子+随机变异算子+全精英选择法;Test3:贪婪算法种群初始化+MPOX交叉算子+HMO、HRO+轮盘赌选择; Test4:贪婪算法种群初始化+MPOX交叉算子+HMO、HRO+全精英选择法.图10分别展示了使用四组实验的GA求解Pcb442的收敛曲线.通过对比收敛曲线Test2和Test1可以看出:在相同遗传代数情况下,采用轮盘赌选择和全精英选择法的GA收敛速度相差不大,然而采用全精英选择法的GA的求解质量总是优于采用轮盘赌的GA,说明全精英选择法对于防止GA陷入局部最优具有较好的效果;通过对比收敛曲线Test3和Test1,采用HMO、HRO的GA寻优速度和质量明显优于采用随机变异算子的GA.由此可知,HMO、HRO有效提升了GA的寻优效率;相较于Test1、Test2和Test3,Test4的收敛速度和求解精度都明显更优.
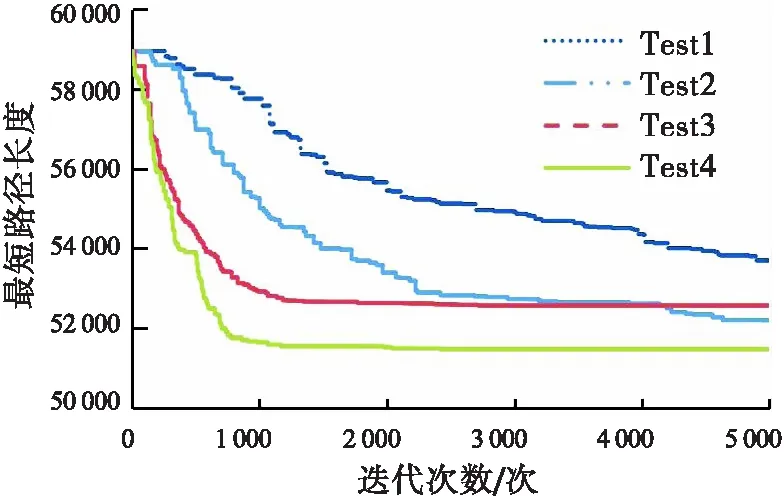
图10 收敛曲线图
为更进一步验证IGA的性能,从标准TSP问题实例数据库TSPLIB中选择21个TSP问题实例进行实验.图11展示了BLS和IGA求解TSP问题实例的平均误差回归曲线,求解误差回归曲线斜率分别为kBLS=0.005 8,kIGA=0.003 1.相较于BLS算法,IGA的求解误差回归曲线斜率更小,IGA的求解误差随着解TSP问题的规模的增大而增加更缓慢.由此说明,IGA的求解性能优于BLS算法.由于其他文献算法求解TSP实例数量较少,在此不做比较.为评价所提出的方法求解TSP问题的精度,采用公式(13)计算误差:

图11 求解误差回归曲线
(13)
式中:Opt表示已知最优解,Mean表示平均解,Err表示平均误差.
表1统计了IGA分别求解21个TSP问题实例10次的最优解(Best)、最劣解(Worst)、平均解(Mean)、平均误差(Err)和平均时间(Time),并与其他研究者论文中采用的算法求解相同TSP问题实例的实验结果进行对比分析.比较算法包括:具有块挖掘和重组启发式的遗传算法(Puzzle-Based Genetic Algorithm,p-ACGA)[4]、混合遗传算法(Hybrid Genetic Algorithm, HGA)[6]、局部搜索算法(Breakout Local Search, BLS)[17]、狼群算法(Wolf Pack Search And Local Search, WPS-LS)[18]、狮子离散群优化算法(Discrete Lion Swarm Optimization, DLSO)[19]、离散社交蜘蛛算法(Discrete Social Spider Algorithm, DSSA)[20].IGA与上述6种算法中求解实例最多且求解效果最好的BLS算法相比,平均求解误差降低了15.36%.

表1 实验结果对比
4 结 论
通过研究选择方法和变异算子对遗传算法求解TSP问题的性能影响,得出如下结论:
1)变异算子是新基因产生的根本途径,优质的启发式变异算子不仅能够提高遗传算法的局部搜索能力,还能加快算法的寻优速度.传统遗传变异算子具有随机性,使算法具有较强的全局搜索能力,但随机变异的方式使算法的效率较低.
2)遗传算法的选择方式关系到种群多样性的发展,种群多样性的增加有利于防止算法陷入局部最优,提高求解精度.虽然传统遗传算法进化模式能逐代积累优势个体,然而种群中重复的优势个体会挤占种群空间,因此可能导致优质基因随劣势个体的淘汰而损失,不利于种群多样性发展.
3)实验结果表明:采用K-近邻域搜索的方式可减少无效搜索,通过变异距离为变异算子寻找有效变异位置,使得变异算子在进行全局搜索时具有较强的局部搜索能力,减少算法寻优时间.通过剔除重复个体再选择优势个体作为新种群会给新个体更大的生存空间,维持种群多样性,有利于防止算法早熟收敛.基于K-近邻域搜索和全精英选择法对提高遗传算法求解TSP问题的性能有显著效果.
