高观点，小学数学教学的时代追求——特级教师周卫东《分数的意义》课例赏析

文 游小云

近日，有幸聆听了全国著名特级教师周卫东一节五年级的数学课——《分数的意义》。教学过程中周老师不断点拨追问，给予学生充分的时间和空间，经历回忆、比较、辨析、变式等过程，循序构建“分数的意义”，培养学生分析、综合、抽象、概括的能力，引导学生深入思考。正如周老师所说“高观点立意，小口径切入”。好课只有细细咀嚼，方能品出独特滋味。

课堂片断一：高观点关注以学生为中心。

师：这节课我们研究什么内容？

生：分数的意义。

师：三年级时，我们两次认识分数，下面来检验一下同学们前面学得怎么样。

图1

师：（指最后一幅图）对于这幅作品，大家有什么好的建议？

生：看不出分的痕迹。这里的4 个圆应该加上一个圈，更容易让我们看出“1”在哪。

【赏析：周老师基于课程内容标准和学生已有经验，按照学生的认知规律进行教学，从顺应教材原有编排的内容结构走向基于学生发展的数学思考，整体思考与设计教学。儿童被看作是由目标指引、积极搜索信息的行动者，他们带着丰富的已有知识、技能和概念进入课堂，而这些已有的知识极大地影响着儿童对周围环境的关注以及组织环境和解释环境的方式。学生带着分数的前概念进入课堂，教师如果忽视学生对分数的初始观念、观点，他们获得的理解可能与教师预期的想法大相径庭。如果学生的初期理解没有被带入其中，那么他们也许不能掌握所教的新概念和信息，否则学生会为了考试的目的而学习知识，但仍会回到课堂之外的前概念。学生对于分数已有初步的认识，课始，周老师唤醒学生的已有经验，请学生画一张图来表示的含义，画图的过程有效唤醒学生对分数的认识，来源于学生的分数作品点燃了学生探究新知的学习欲望。在师生共同欣赏分数作品的过程中，对于的不完整表达（如图2），学生上展台修改（如图3、图4），首先通过画圈，让大家更容易看出单位“1”，然后增加两条虚线，让其余学生一眼看出平均分成4 份。周老师帮助每个学生对“研究分数的过程中，前提是要平均分”达到更成熟的理解。建构主义认为不管如何教一个人，所有的知识是基于已有的知识而建构起来的。诸多证据表明，如果教师关注学习者带到学习任务中的已有知识和观念，将这些知识作为新教学的起点，并在教学过程中监控学生概念的转化，那么就可以促进学生的学习。在“比较三幅作品的画法不一样，却都能表示，有什么变与不变的地方？”时，这一过程凸显出只要“把1 个整体平均分成4份，取其中的3 份”，就能用分数表示。师生在欣赏分数作品的过程中学生学习兴趣浓厚，积极合作、主动探究对这一特殊分数的理解，从一个图形、几个物体组成的一个整体、一个计量单位迁移到单位“1”；从的意义到具体情境中多个分数的意义，最后抽象出分数的意义；培养学生的抽象概括能力，发展学生的数学思维，充分体现了周老师以学生为中心，以学生的经验为中心，以学生的活动为中心的教学设计理念。】

图2

图3

图4

课堂片断二：高观点倡导对话教学方式。

师：其实一个物体、一个计量单位、许多个物体组成的一个整体，它们有一个共同的名称，称作单位“1”。回顾一下，单位“1”有哪几种类型呢？

生：单位“1”有一个物体、一个计量单位、许多个物体组成的一个整体三种类型。

师：你还能再举一些单位“1”的例子吗？

生：一群牛、全校学生……

师：（认识了几个具体情境中的分数之后）同学们能不能概括一下究竟什么是分数呢？

生：把单位“1”平均分成x份，表示其中的n 份。

师：很强的符号意识，如果用文字表示呢？

生：若干份。

师：真有预见性。表示这样的——，用什么词好呢？

生：1 份或几份。

师：你是怎么想的？

生：因为把单位“1”平均分成若干份，可以表示1 份，也可以表示几份。

【赏析：在本课教学中，教师和学生的关系不再是以知识为中介的主体对客体的单向灌输关系，不再是教师选择内容，学生适应学习内容的关系，而是一种教学对话关系。教学过程可以看作是人和文本、教师和学生、学生和学生之间的对话。现代教育观的教学，把教材看作对话的“文本”，教学就是人与文本的对话，包含师生和教材、教师和学生、学生和学生对话，在对话中创生学习内容。通过分数意义的整体分析与重构，指向学生把握数学结构，打破按部就班的传统教学方式，实现“用教材教”而非“教教材”。周老师针对学生好奇的心智特征，教学设计立足于学生心智发展需要和认知发展水平，对教材资源开发、利用、重构及整体设计，满足学生数学思维发展的需要，设计灵活多样的教学对话，尊重个体差异，避免“一言堂”和“满堂灌”的情况。

在教学过程中，周老师设计了一道发展学生求异思维的练习题。（如图5）这一练习促成教师与学生、学生与学生、学生与分数文本的多层次对话。可以是“把单位‘1’平均分成3 份，涂色部分表示其中的1 份，即”，也可以是“把单位‘1’平均分成6 份，表示其中的2 份，用表示”，还可以是“把单位‘1’平均分成12 份，表示这样的4 份，即”。学生随后在第二次“变与不变”的对话中感悟到：同样的单位“1”，不同的分法就能得到不同的分数；分的份数越多，每一份代表的数就越小；阴影部分没变，三个分数的大小相等……既有学生和练习文本的对话，又有学生和学生间不同思维的对话，还有教师和学生的对话，更有学生与自我思维的对话，通过对话过程丰富了学生对分数意义的理解和掌握。】

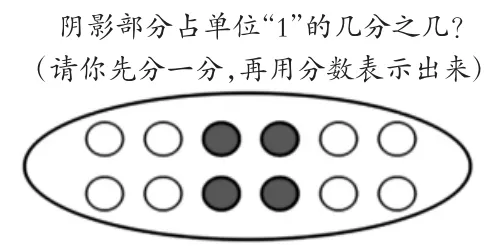
图5

课堂片断三：高观点追求概念理解目标。

师：同学们，分圆片中有变与不变，游戏中也有变与不变。（出示A、B 两个袋子，其中装有一些圆片，分别发给同桌两位同学）数一数一共有多少个？

（A 袋学生贴出5 个，B 袋学生贴出3 个）

生：两个袋子里的单位“1”不一样。

师：请算一算，A 袋的单位“1”是多少？B 袋的单位“1”又是多少？

生：A 袋10 个，B 袋6 个。

师：请两位同学把袋子里的圆片都摆上黑板，公布答案。

（A、B 两袋学生分别摆出2个圆片）

师：同学们看一下他们取的结果，如果你是数学老师，你可能会问一个什么数学问题？

生：为什么分数不一样，拿出的个数却是一样的？

师：谁能回答这个问题？

生：因为它们的单位“1”是不一样的。

师：不一样的单位“1”，不一样的份数，但是他们取出的个数可能是一样的。

【赏析：美国教育心理学家布鲁纳认为：不论教什么学科，都必须使学生理解学科的基本结构，即各门学科的基本概念、基本原理以及它们之间的联系。高观点下的数学教学设计不仅需要了解数学内容本身，还需要了解数学学科的内容结构。周老师根据学生的实际学情，基于“高观点”整体教学视角，研读课程、学段、年级、单元、课时等不同层面的教学资源，分析教学内容及价值，重构教材编排。教学设计的出发点是班级实际学情，包括学生的知识背景、生活经验、年龄和心理特征、学习的需要等，凸显分数的意义结构性、整体性和连续性。教学的着眼点是分数的意义，观点却是数学模型和数学思想，把数学的两个基本对象“数”和“形”有机结合起来。在建立分数模型的过程中，分数的意义在知识技能、数学思考、问题解决和情感态度等方面建立知识结构的横向联系。在知识技能方面，分数的意义得到进一步扩展，在分物活动情境中用分数刻画现实生活现象；在数学思考方面，抽象的分数意义使学生数学思维能力有更大的发展空间；在问题解决方面，分数既能表示部分与整体的关系，又能表示分数是由分数单位累计的数，（课后周老师表示之所以这节课没有涉及分数单位的内容，是想用一节课教学分数单位，从度量角度进一步丰富分数的意义）学生在构建分数模型的过程中进一步提高分析、综合、抽象和概括的能力；在情感态度方面，对分数的意义、价值、性质的探究有更深刻的理解和体验。

周老师的教学设计关注学生的数学理解及程序流程，关注学生的思维，利用已有内容生成或揭示有意义的事情，即利用已有的知识经验去发掘事实和方法背后的含义并谨慎地加以运用，重组单元内容、重构教学内容体系，联系学科的基本概念和原理，指向数学理解进行教学设计。同时，本课教学过程中也渗透了“运算”意义，如10 个圆片的是2 个，6个圆片的是2 个，把16 个圆片都摆在一起，成为一个大的单位“1”，请学生取圆片，打算取几个，是16 个圆片的几分之一？这一开放性练习采用学生喜欢的游戏方式，激发了学生学习分数的兴趣与热情，提升了学生对分数本质的认识，只要把“单位‘1’平均分成若干份，表示这样的一份或几份，可以用分数表示”，而且通过第三次辨析“什么变了，什么不变”，在“变与不变”中凸显分数的意义本质。

将“冰冷的分数意义”化作“火热的数学思考”，离不开周老师高观点视角的教学设计和充满智慧的师生对话与课堂组织。以学生为中心、倡导对话方式、追求概念理解，体现出周老师先进的教学理念和精湛的教学艺术。】