让学生学习『讲道理』的数学

文 高飞

道理，《现代汉语词典》解释说：①事物的规律；②事情或论点的是非得失的根据；理由；情理；③办法；打算。让学生学习“讲道理”的数学，一方面是指引导学生发现数学知识的本质规律;另一方面是指促动学生阐明数学知识产生、发展和形成的依据或理由，等等。让学生学习“讲道理”的数学，不仅有助于学生“触摸”数学知识的本质，提升数学知识的理解水平，而且有助于学生明确数学知识规定的合理性，理解基本技能操作的程序与步骤的道理，培养学生地数学思维能力。综上所述，在数学学习中，引导学生发现与诠释数学知识产生、发展、形成和应用的道理，是实现数学深度学习目标的重要措施之一。那么，在数学教学中，如何引导学生学习“讲道理”的数学，达成深度学习的目标呢？

一、立足本质“讲道理”，促进学生理解概念的内涵

概念教学是小学阶段重点教学内容之一。概念教学的要求是使学生经历概念的产生、发展和形成的过程，促进学生理解概念的本质内涵，达成“知其然，又知其所以然”的目标。为此，在概念教学中，教师要从概念的本质属性出发，设计适当的教与学的活动，引导学生经历对概念例证的观察、操作、推理、抽象、概括和交流等认知活动，通过讲好概念形成的道理，促进学生体验概念的本质属性，达成对概念内涵的深刻理解。

点到直线的距离（苏教版数学四年级上册）是图形与几何领域的重要概念之一。它是学生认识各类图形的高的认知基础。众所周知，数学上，之所以确定从已知点到已知直线的垂直线段作为点到直线的距离，其根本原因是它的唯一属性，而非长度最短的特征。为此，教材先是从已知点向已知直线引出若干条线段，然后，通过测量活动，引导学生探索并发现在这些线段中，与已知直线相互垂直的线段的长度“最”短。力求从词意上，通过“最”字的体悟，帮助学生感受与已知直线相互垂直线段的唯一性。为此，在实际教学中，通常采取的教学路径是：出示从已知点到已知直线的若干条线段—引导学生猜测哪条线段最短—通过测量进行验证，得出结论—揭示点到直线距离的概念。不难看出，不管是猜测环节，还是验证环节，学生的注意力及其探究聚焦点无不集中在“线段的长度”上，从而“短”字成为了探究学习过程中的“强刺激”，而体现与已知直线相互垂直线段的唯一性的“最”字的感悟，无形中被“弱化了”。最终，通过系列活动，学生只是强烈感受了“垂直线段最短”。无疑，学生的体会和教材的编排意图“相距甚远”。那么，如何帮助学生体会点到已知直线的垂直线段的唯一性，进而帮助学生理解点到直线的距离的内涵呢？

出示图1：

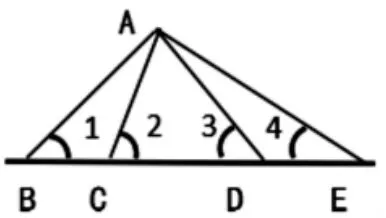
图1

如图1，在已知直线上任取点B，连接点AB，线段AB 和已知直线的夹角为∠1，接着，继续画出线段AC、AD 和AE，夹角分别是∠2、∠3 和∠4。

互动1：像AB、AC、AD 和AE这样，从A 点到已知直线的线段，能画多少条？为什么？

引导学生从“直线上有无数个点”，或者重点从“像AB、AC、AD 和AE 这样的线段与已知直线的夹角，如∠1、∠2、∠3 和∠4 都是锐角，因为锐角有无数种，所以，这样的线段能画无数条”的角度，理解及阐述像AB、AC、AD 和AE 这样的线段有无数条的道理。

互动2：从A 点到已知直线的线段中，“有且只有一条”的线段在哪里？它与已知直线有什么关系？找一找、画一画，说明理由。

引导学生借助图形，找出与已知直线互相垂直的线段（如图2，AF），并从“AF 与已知直线的夹角是直角，直角是唯一的”的角度，说明线段AF 的唯一性。

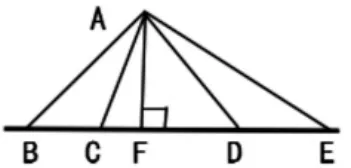
图2

互动3：量一量AB、AC、AD、AE 和AF，你有什么发现？

通过测量，使学生认识“从直线外一点到已知直线的垂直线段是最短的”的特征。

最后，揭示点到直线的距离概念。

角是学生熟悉的知识。特别是，经历小数的初步认识、角的测量和分类等知识技能学习以后，学生对“锐角有无数个”“直角是唯一的”的认识更加充分而深入。为此，案例中，教师“另辟蹊径”从学生已有的“角”的经验出发，引导他们借助“锐角有无数个”“直角是唯一的”的认知与体验，通过推理和想象等活动，感受从直线外一点到已知直线的线段中，与已知直线互相垂直的线段“只有一条”的特性，从而助力学生体会点到已知直线的垂直线段的唯一性，促进学生理解点到直线的距离的内涵，更重要的是，自始至终引发了学生思维活动的深度参与，达成了深度学习的目标。

二、立足意义“讲道理”，促进学生理解计算的道理

运算能力主要是指能够根据法则和运算律正确地进行计算的能力，培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。因此，计算教学在促使学生熟练掌握算法的同时，还要促进学生理解计算的道理。然而，教学假分数化成带分数（苏教版数学五年级下册）时，教师通常是不讲“道理”的。学生往往仅凭教师的简单传授“分子除以分母的‘商’作带分数的整数部分，‘余数’作分子，‘分母’不变”进行模仿和操练。试想：“假分数化成带分数用分子除以分母，为什么‘商’‘余数’分别是带分数的整数部分和分子，分母不变呢？”对这些问题的思辨、解释和澄清，正是学生学习假分数化成带分数必须经历的、不可省却的思考过程！否则，就嬗变为“知其然，而不知其所以然”的机械学习。为此，教学中，教师可以借助几何直观手段，引导学生自主构图并利用图形诠释假分数化成带分数的“算理”：

互动1：分子不是分母的倍数的假分数，怎样化成带分数？试一试。

生1：

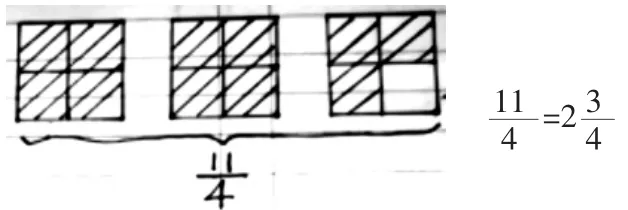
图3

互动2：（指生2）能不能借助生1 的图形，说说你是怎样想的？

接着，让学生“趁热打铁”继续将几个假分数化成带分数，并发现把假分数化成带分数“用分子除以分母的商作带分数的整数部分，余数作分子，分母不变”的规律。

假分数化成整数和带分数的“算理”理解，需要学生从“包含除”的视角进行探索与思考。案例中，把化成带分数。有的学生通过构造图形描述，从而“看”出；有的学生联系分数与除法的关系，通过11÷4=2……3，推导出。为此，教师巧妙利用生成“资源”追问生2：“能不能借助生1 的图形，说说你是怎样想的？”板演学生“心有灵犀”，借着图形，有根有据地阐明了的数学道理，同时，欣然理解：“为什么要每4 个分成一份呢？而不是2 个、3 个？”从而突破了假分数化成带分数的“算理理解”的难点，达成了深度学习的目标。

三、立足需要“讲道理”，促进学生理解操作方法的合理性

《数学课程标准（2011年版）》指出：“在基本技能教学中，不仅要使学生掌握基本技能操作的程序和步骤，还要使学生理解程序和步骤的道理。”画平行线是小学数学学习的重要技能之一，教材（人教版数学四年级上册）基本上是采取“直接告知”的方式进行教学的。即以“图示”的方式，在分步演示选择什么工具，怎样操作的基础上，引导学生讨论、归纳操作步骤和方法。但是，画平行线的基本原理是什么？作图时，可能遇到什么困难？为什么用两把尺子“合作”等等，对这些问题的体验、质疑和阐释，正是学生理解画平行线的方法和步骤需要经历的、不可逾越的思考过程。那么，在教学中，如何引导学生体会平移和平行的关系，经历画平行线的工具选择、方法优化、画法概括等思维过程，促进学生理解操作的合理性？

动画出示：

图4

互动1：说说推拉窗和五星红旗分别是什么运动？用铅笔在方格纸上移一移、画一画，你发现了什么？

引导学生用铅笔在方格纸上，模仿推拉窗和五星红旗的运动轨迹，移一移、画一画，使学生体验平移和平行的关系，促进学生认识通过平移可以得到两条互相平行的直线。

互动2：你能在纸上，利用平移画出两条互相平行的直线吗？试一试，你有什么感受？

通过操作，促使学生体验利用直尺或三角尺进行平移时，会出现“偏轨”现象，产生解决问题的心理需求。

互动3：想一想，有什么改进的办法吗？议一议。

激发学生积极调用已有经验，优化工具，改进操作方法：在三角尺的另一条直角边上，贴紧一把直尺或三角尺作“轨道”，平移时不会发生“偏轨”的现象，体验选用两把尺子的必要性，理解画平行线的方法。

互动4：你能画出一组互相平行的直线吗？说一说画平行线时，要注意什么？

利用改进后的操作工具及其方法，画一组互相平行的直线，并总结画平行线的方法（略），促进学生体验选择工具的必要性及其操作方法的合理性。

案例中，通过动画演示两组平移的现象，同时，引导用铅笔在方格纸上模仿两组平移现象画出两组平行线，促使学生体会平移与平行的内在联系，认识通过平移方式可以画出一组互相平行的直线。在此基础上，引导学生自主选择工具，通过在纸上画平行线，促进他们体验用一把尺子进行平移画平行线的局限性，产生认知冲突，形成“迫切”解决问题的心理需求，从而促动学生积极讨论改进画平行线的操作工具及其方法。整个教学过程，学生经历了平行线的画法及工具的选择、优化与调整的反思、尝试等思维过程，深刻体会了画平行线工具选择的必要性及其操作方法的合理性，达成了“知其然，又知其所以然”的目标，积累了尺规作图的活动经验，提升了操作能力。