以“辩”促“思”，助推深度理解——以《分数乘除法解决问题》练习课教学为例

文|朱 燕

在小学数学教学中实施“辩证式”教学，可提高学生的学习能力和思维品质, 促进学生的深度理解。下面笔者以《分数乘除法解决问题》练习课教学为例，谈谈如何通过“辩证教学”促进学生思维发展，助推学生深度理解。

一、分析学生：在错题研究中发现“辩证需求”

作为“解决问题”教学中的重要组成部分——“分数乘除法解决问题”历来是学生学习的难点。

1.学生错题的问诊。

通过分析研究学生作业发现：学生在学完《分数乘除法解决问题》之后，进行综合练习时，错误率较高的主要原因是：

数量关系比较复杂。例如，“学校科技组有60 人，比书法组少，书法组有多少人？”这题的错误率比较高。其中“比书法组少”是学生理解的难点，很多学生不理解关键句中的数量关系（单位“1”的辨认错误；比较量对应的分率辨认错误；单位“1”与比较量的关系分析错误），导致无法正确解决问题。

相关题目类型多样。在同一情境中，“分数乘除法解决问题”可以变换出多种不同类型的题目，且题目的难易程度也不同。从解题方法看：有些题目用分数乘法计算，有些用分数除法计算，还有些用乘加乘减计算，也有用列方程来计算；从题目难度分，可以分为简单、稍复杂和复杂三类。这对于概念不清的学生来说，理解起来确实有困难。

同一题型方法多样。即使是同一道题，也会出现用多种方法来解决。解题方法多样化拓宽了学生的解题思路，但也正是因为解题方法的多样化，使得部分学生被此所迷惑，个别学生原本就对数量关系分析有困难，再遇到多样化的解题方法，就又增加了学习的难度。

2.辩证思维的需求。

这些对立、多样的因素导致了学生对“分数乘除法解决问题”理解不到位，出现了易混淆出错的情况。但复杂的数量关系间存在联系，多样化的题型中具有共性，多样化的方法里本质相同，这说明“分数乘除法解决问题”存在“对立统一”的辩证关系。如果能够借助这一辩证关系，把复杂的数量关系简单化、多样的问题题型模型化、多样的解题方法沟通化，那么就能大大降低学习难度，同时培养学生的辩证思维，提高学生的解题能力。

为此，笔者将从“分数乘除法解决问题”所蕴含的“对立统一”辩证关系入手，深入研究问题，以“辩”促“思”设计教学，引导学生以“辩”悟“联”，发展学生的“辩证思维”，助推学生对数学知识的深度理解。

二、追本溯源：在教学内容中寻找“辩证方法”

为了帮助学生更好地理解“分数乘除法解决问题”，提升学生的解题能力，笔者纵观“分数乘法”与“分数除法”的教学内容，寻找能够使“复杂的数量关系简单化、多样的问题类型模型化、多样的解题方法沟通化”的教学方法，力图构建“对立统一”的辩证关系，帮助学生正确理清数量关系，形成解决问题的解题模型，沟通多样化算法之间的联系，从而促进学生的深度理解。

1.“观”问题关键句，“探”辩证式的数量关系。

题型多样的“分数乘除法解决问题”中，关键句具有相似性，可将其分类归纳成两类典型的关键句，分别是：一个数是另一个数的几分之几；一个数比另一个数多（少）几分之几。

这两类关键句虽然形式不同，但表示的数量关系本质意义相同，存在“对立统一”的辩证关系。其中第二类的数量关系比第一类更复杂，是学生学习的难点。

借助乘法分配律，我们可以把稍复杂的“一个数比另一个数多（少）几分之几”的数量关系转化成“一个数是另一个数的几分之几”的数量关系，这样就把复杂的数量关系简单化了，可以大大提高学生的分析能力和解题能力。

归纳这两类关键句中的所有数量关系，可整理成以下三种：一个数是另一个数的几分之几；一个数比另一个数多几分之几；一个数比另一个数少几分之几。这些数量关系本质上都在研究“比较量”与单位“1”的“倍数问题”。只是第一个关键句中的分数表示“比较量”对应的直接分率，因此可以直接与单位“1”相乘；第二、三个关键句中的分数表示“比较量”对应的间接分率，所以先要把间接分率转化成直接分率后再乘单位“1”进行计算。

可见，只要把复杂的“一个数比另一个数多（少）几分之几”转化成“一个数是另一个数的几分之几”，再分析其数量关系就非常容易了。辩证研究数量关系降低了学生分析关键句列数量关系的难度，而正确列出数量关系又是正确解答“分数乘除法解决问题”的保障。

2.“析”多样化题型，“构”辩证式的解题模型。

根据关键句中单位“1”的已知和未知，可以构建“分数乘除法解决问题”的解题模型。因为单位“1”×比较量对应的分率=比较量，所以当已知单位“1”时，用“分数乘法解决问题”；当未知单位“1”时，用“分数除法解决问题”。

利用两类典型关键句中“对立统一”的辩证关系，可以把稍复杂的“分数乘除法解决问题”转化成简单的“分数乘除法解决问题”。

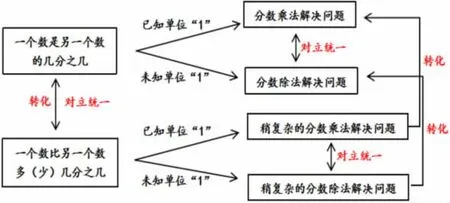
把稍复杂的关键句转化成简单的关键句，这就把稍复杂的“分数乘除法解决问题”转化成了简单的“分数乘除法解决问题”，两者之间“对立统一”的辩证关系是建立“分数乘除法解决问题”解题模型的关键。

3.“品”多样化算法，“创”辩证式的解题方法。

在多种“分数乘除法解决问题”的题型中，“稍复杂的分数除法解决问题”错误率最高，因为这类题型的解题方法最多。方法多样化是一把双刃剑，方法越多，越需要学生理解它们的区别与联系，要求学生能够透过多样化方法的表象，抓住解决问题的本质，从而游刃有余地利用多样化方法正确解决实际问题。

“稍复杂的分数除法解决问题”有三种解题方法，分别是一种“分数除法解决问题”和两种“列乘法方程解决问题”。其中两种方法的解题过程不同，但其内在的数量关系是一样的。第三种方法的数量关系与前两种略有不同，不过根据乘法分配律可以相互转化，由此得出，这三种方法存在着“对立统一”的辩证关系。

通过对比沟通这三种不同方法之间的联系，构建辩证关系，能帮助学生理解“分数除法解决问题”可以用“列乘法方程”解决的原因，感受到三种方法的区别与联系，掌握多样化的解题方法。

4.“思”乘除法意义，“明”辩证式的计算原理。

“分数乘除法的意义”是“分数乘除法解决问题”的基础与核心，学生只有理解意义，体会两者“对立统一”的辩证关系，才能在解决问题中合理地选择适当的计算方法解决问题，并能实现解决问题的方法多样化。

“分数乘法意义”与“分数除法意义”既是对立的，又是统一的，两者存在两层“对立统一”的辩证关系。

关系1：分数除法是分数乘法的逆运算。这是由除法的概念决定的。除法的意义表示已知两数的积与其中一个因数，求另一个因数的运算。这个概念就是在乘法概念的基础上衍生而成的，所以乘除法之间存在“对立统一”的辩证关系。

关系2：除以一个数等于乘这个数的倒数。这是由分数的意义决定的。因为分数的意义是把单位“1”平均分成几份，表示这样的一份或几份的数叫作分数。而平均分又是除法的内在含义，由此就有了“除以一个数等于乘这个数的倒数”的计算方法，也就让分数乘法与分数除法有了另一层“对立统一”的辩证关系。

同一个数量关系之所以能写出三种解题方法，正是因为“除法与乘法”意义中的辩证关系。因为除法是乘法的逆运算，所以可以借助方程把逆向思维的“分数除法解决问题”转化成顺向思维的“列分数乘法方程解决问题”。这有助于学生理解算理，掌握算法。而“分数除法与分数乘法”独有的辩证关系是正确计算分数除法的保障，只有掌握这层辩证关系，学生才能正确计算“分数除法解决问题”。

三、实践研究：在教学环节中培养“辩证思维”

1.转化“问题关键句”，构建辩证关系，降低学习难度。

【环节设计】在这个环节中，笔者设计了找单位“1”、列数量关系的任务。让学生根据这三个数量关系说一说：

（1）谁是单位“1”？

（2）你知道它所表示的数量关系吗？画图验证。

（3）对比观察，你能发现这些数量关系之间有什么联系？

通过对比观察，可以引导学生发现不同事物之间可能存在一定联系，引导学生用“对立统一”的观点去分析问题和解决问题，学会把复杂的关键句简单化，降低学习难度，为接下来的解题建模做铺垫。

【设计意图：对比分析数量关系，发现其“对立统一”的辩证关系。】

2.研究“多样化题型”，孕育辩证思维，建立解题模型。

多样化题型能够驱动学生产生差异与对立的想法，当见解产生差异与对立时，会激发争辩与讨论，由此产生新的发现与见解就是“辩证思维”形成的过程。

（1）自主编题，形成素材。

教师出示研究问题，学生自主编题解答。

根据关键句，你能自己设计条件和问题，编写一道解决问题并自己解决吗？

（2）分类辨析，总结题型。

每位学生设计的条件和问题不可能完全相同，但由于题目中的关键句相同，使得学生设计的题目既有差异性又有相似性，形成具有研究价值的辩证素材。辩证素材具有思辨性，分类辨析这些素材有利于激发学生的探究意识，引发学生的质疑和讨论，孕育学生的辩证思维。通过分析对比学生的作品，就能把全班同学编制的题目按题目类型进行分类。

根据关键句中单位“1”的已知和未知，可以构建“分数乘除法解决问题”的题型。利用关键句中辩证关系，可以把“女生比男生少”转化成“女生是男生的”是正确分析其数量关系解决问题的关键。

（3）发现联系，构建模型。

通过分类辨析，我们已经把开放性的问题总结成四种题型。其实，借助辩证关系，我们还可以把这四种题型统一成一种解题模型：找单位“1”——男生人数；数量关系——男生人数×（1-）=女生人数；根据数量关系，列算式或方程计算；反思检验并写出结论。

【设计意图：从现象到本质，从对立到统一，培养学生用联系的眼光寻找不同题型共性的解题模型，是强化学生辩证意识的有效途径。】

3.聚焦“算法多样化”，强化辩证意识，优化解题方法。

其中，题型3 和题型4 是学生的易错题，也是部分学生理解的难点。例如，男生有250 人，女生比男生少，女生比男生少几人？正确的解题方法有两种：

对比两种方法，第二种方法优于第一种。这就是要学生理清解决问题的关键是理清数量关系，正确把握谁是比较量，比较量对应的直接分率到底是多少。

【设计意图：将不同的题目进行分类、辨析、总结、建模、优化，不仅提高了学生的解题能力，还发展了学生的辩证思维，促进了学生的深度理解。】

4.研究“乘除法算式”，提升辩证能力，发展学生素养。

“乘除法算式”是“分数乘除法解决问题”的外在表象，数量关系是其内在本质，但表象与本质之间是可以双向交流、互相转化的。对此，笔者设计了通过“乘除法算式”分析数量关系、编写关键句的练习，力图通过逆向思维，提升学生的辩证能力，发展学生的学科素养。

（1）类比对照，迁移与应用同推进。

【问题设计】小明有故事书42 本__________，，漫画书有多少本？

根据算式，补充信息。

【设计意图：此题是一道逆向练习，能培养学生的逆向思维和辩证思维。在类比对照中，巩固学生以单位“1”的已知与未知判断解决问题的计算方法，也能反向迁移，凭借算式判断单位“1”的已知与未知，了解比较量对应的分率，实现迁移与应用的共同发展，提高学生的解题能力和辩证思维能力。】

（2）个性创造，创新与技能共发展。

【问题设计】小明有故事书42 本，__________，漫画书有多少本？

如果在补充的关键句中要出示分数，你还能想到哪些关键句？你会自己列式解决吗？（只列式不计算）

【设计意图：设计解决开放性的解决问题能体现学生的个性化，可培养学生的创新能力和解题能力。同一情况下的多样化题型是学生自主创新的智慧结晶，灵活解决多样化题型是学生技能提升的体现。】

（3）对比强化，能力与思维双提升。

分类汇总学生的作品，如图：

纵向观察：已知单位“1”，用分数乘法解决问题，如图中的①③⑤；未知单位“1”，用分数除法解决问题，如图中的②④⑥。

横向观察：“一个数是另一个数的几分之几”的算式是单位“1”×（或÷）分率=比较量，如①和②；“一个数比另一个数多几分之几”的算式是单位“1”×（或÷）（1+分率）=比较量，如③和④；“一个数比另一个数少几分之几”的算式是单位“1”×（或÷）（1-分率）=比较量，如⑤和⑥。

四、对比评价：在前后测试中检验“教学成效”

笔者采用“范希尔理论”的五个思维水平，对学生练习前后的思维水平层次进行了界定及赋值，以此来检测教学前后学生思维水平的变化，检测教学的有效性。通过测试结果的分析研究，笔者认为，上述辩证式的练习课教学，以“辩”促“思”，打通了两个单元解决问题中的“隔断墙”，让学生在活动探究中理解了这两类问题的辩证关系，掌握了两种题型的解题方法，发展了用“对立统一”观点看问题的“辩证思维”。

经过本节课的教学，学生对用分数乘、除法解决的问题类型有了较为深刻的认识，对两者的辩证关系有了体验和认知。这种认知提升了学生解决问题的能力，也促进了学生“辩证思维”的发展。