Entanglement witnesses of four-qubit tripartite separable quantum states*

Miao Xu (徐淼), Wei-Feng Zhou (周伟峰), Feng Chen (陈峰),Li-Zhen Jiang (蒋丽珍),** and Xiao-Yu Chen (陈小余)

1 College of Information and Electronic Engineering, Zhejiang Gongshang University, Hangzhou 310018,China

2 School of Information & Electrical Engineering, Zhejiang University City College, Hangzhou 310015,China

Abstract A quantum entangled state is easily disturbed by noise and degenerates into a separable state.Compared to the entanglement with bipartite quantum systems,less progress has been made for the entanglement with multipartite quantum systems.For tripartite separability of a four-qubit system, we propose two entanglement witnesses, each of which corresponds to a necessary condition of tripartite separability.For the four-qubit GHZ state mixed with a W state and white noise, we prove that the necessary conditions of tripartite separability are also sufficient at W states side.

Keywords: tripartite separability, entanglement witness, GHZ state, W state

1.Introduction

Quantum entanglement [1] as an extremely crucial resource[2] has potential applications for quantum computation and quantum communication.A quantum state is only known as separable if it can be generated by local operations and classical communications (LOCC) only, otherwise it is entangled.It is particularly significant to have a criterion that can systematically determine whether a given quantum state is entangled or separable.In 1996, Peres first put forward positive partial transition(PPT)[3]criterion,later,Horodecki proved that PPT criterion is not only necessary but also sufficient in theH2⊗ H2andH2⊗ H3systems.For example,a quantum state ρ has elements ρμκ,νι=〈μ|〈κ|ρ|ν〉|ι〉, if its partial transpositionis positive, the state is separable [4].However, in some high dimensional quantum state systems, such asH3⊗ H3andH2⊗ H4, the transposition of some entangled state is also positive[5].It shows that PPT criterion may no longer be sufficient for the separability of high dimensional and multipartite quantum states.Another separable criterion, the computable crossnorm or realignment(CCNR)criterion which can detect some other entangled states is regarded as a complement[6]to PPT criterion.Range criterion [7]and some other criteria had also been proposed.However, there is an obvious defect within the range criterion that the density matrix of the quantum state and its partial transposition are generally full rank in a noise environment,which makes the criterion no longer applicable.Quantum Fisher information (QFI) [8–10] has been used in the detection of the entanglement and the k-nonseparability of multipartite quantum systems.Entanglement witness [11] is also widely used and appropriate for multipartite systems in entanglement detection [12–17].Theoretically, an entanglement witness exists which can be a sufficient and necessary condition for detecting entanglement.The entanglement witness is essentially an observable Hermitian operator, we havefor all separable quantum state ρsand there is at least an entangled state ρesuch thatwe assert that the state ρeis witnessed by[18].Then the task of detecting entanglement is transformed into searching for an entanglement witness.

we call it k-separable [26, 27], where ∣I ∣is the number of elements of set I, andis a classical probability distribution.In the four-qubit triseparable system, if qubits 1, 2, 3, 4 exist, we divide the first and second qubit into the first and second part respectively, and the third and fourth qubits as the third part,which is denoted as |1|2|34|.Consequently the pure product state is

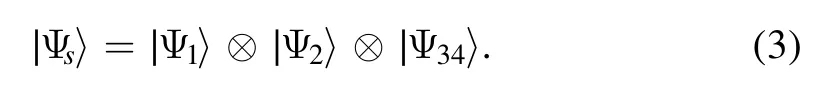
In computational basis, a single qubit pure state is

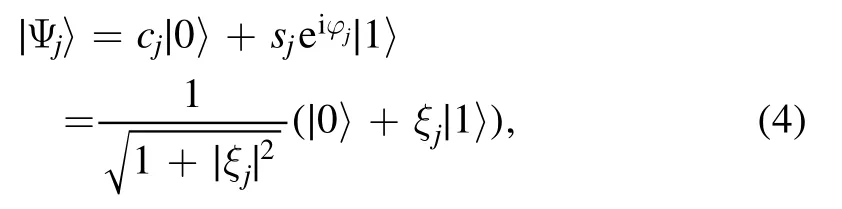
The paper is organized as follows.In sections 2 and 3 we propose two entanglement witnesses, respectively, each of which corresponds to a necessary condition of tripartite separability for any four-qubit quantum state.We conclude in section 4.GHZ states [28] and W states [29] as the common multipartite entangled states are often used in quantum information processing.Additive white noise has been introduced to describe the effect of the environment on a quantum state.The density matrix of a four-qubit GHZ state mixed with a W state and white noise (denote as noisy GHZ-W state) is

2.The first entanglement witness

We propose the first entanglement witness.We arrange the order of four qubit computation basis |k〉 with the ascending order of |k|.In such a basis, the 16×16 matrixis defined as

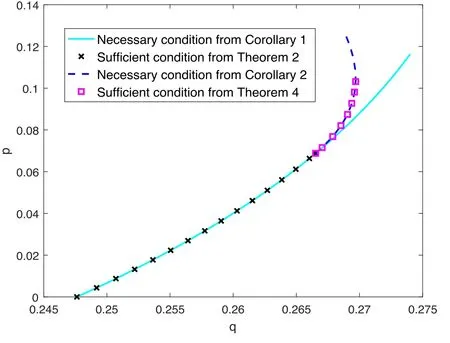
Figure 1.Necessary and/or sufficient criteria for the triseparability of state ρ = p∣GHZ〉〈G HZ∣ + q∣W

Corollary 1.A necessary condition of tripartite separability for a noisy GHZ-W state is

Proof.According to Theorem 1,we can obtain the result for a noisy GHZ-W state as follows:

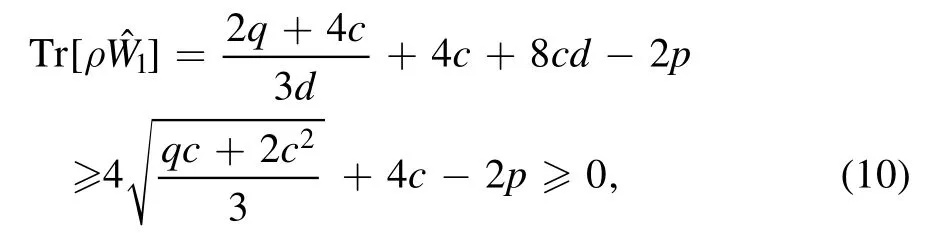
Theorem 2.For a noisy GHZ-W state,the necessary criterion of tripartite separability in corollary 1 is also sufficient in the parameter interval of Θ ∈ [0, 0.080401π].

In the type I and type II, the density matrices are ρIand ρIIrespectively, where ρI(ρIIis similar) can be written as

The results are

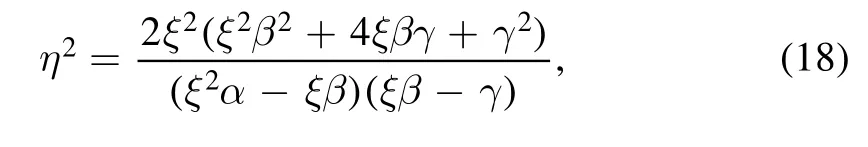
and

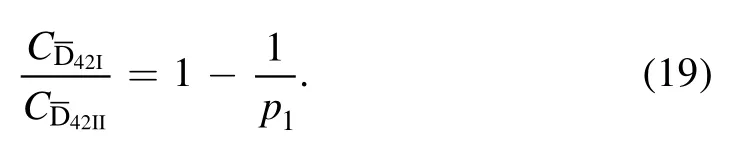
Combining with equation (23), then

We get Θ ≈0.080401π, namely the upper bound distinguishing the sufficient condition and the necessary condition.When y1=y2, we can get Θ ≈0.024073π, i.e.the lower bound.In all, the sufficient condition is consistent with the necessary condition in Θ ∈[0.024073π,0.080401π].Next we will consider the case in Θ ≤0.024073π, and there is little difference in step 1 and 2 compared to above processes.

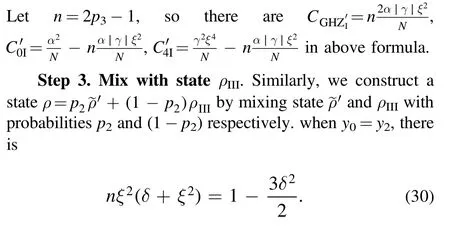
The value ofrmaxcan be deduced to

The sufficient condition of tripartite separabilityr≤rmaxis equivalent to the necessary condition after a simple transformation within Θ ∈[0, 0.024073π].At last, the necessary condition in Corollary 1 for a four-qubit noisy GHZ-W state is also sufficient in Θ ∈[0,0.080401π].And the sufficiency is displayed with the black cross line in figure 1.

3.The second entanglement witness

We propose the second 16th order witnesswhich is

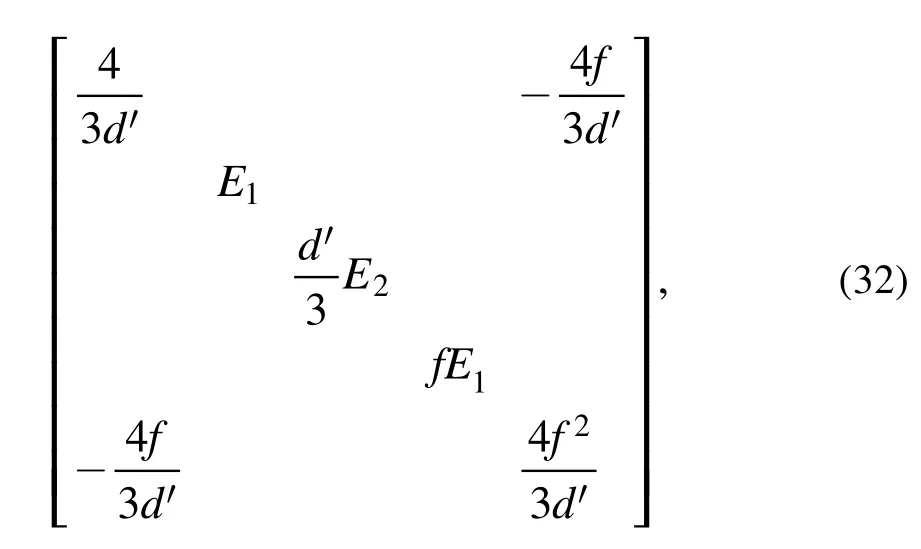
in the basis |k〉 with the ascending order of |k|, wheref＞ 0,d′ ＞ 0with,and the matrices E1and E2refer to equation (6), and other unidentified elements are zeros.

Theorem 3.For any four-qubit quantum state ρ, another

necessary criterion of tripartite separability isTr≥ 0.

Corollary 2.Another necessary condition of tripartite separability for a noisy GHZ-W state is

wherec= 1-p-q, with

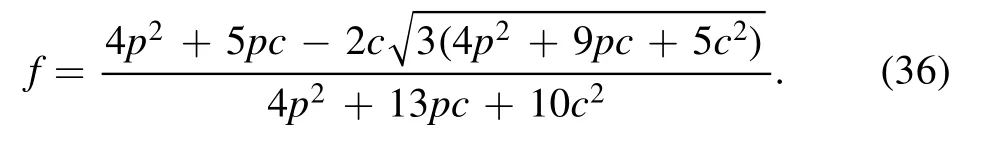
Theorem 4.For a noisy GHZ-W state,the necessary condition of tripartite separability in corollary 2 is also sufficient in the parameter interval of Θ ∈ [0.080401π, 0.11628π].

The construction of the triseparable states can also be divided into the following three steps:

4.Conclusion

In a four-qubit system, bothTr≥ 0andTr≥0 are the necessary criteria of tripartite separability for any quantum state ρ.For a four-qubit noisy GHZ-W state,we get two necessities of tripartite separability at |W〉 state side.In the derivation of sufficiency,we make use of the eigenvectors corresponding to zero eigenvalues of some matrices derived from witness to construct quantum states for the aim of obtaining boundary hypersurface distinguishing separable states from entanglement states.Significantly, the pure product state |Ψ〉 constructed by entanglement witness should read= 0, noise Dias a special case of the optimal product states should also satisfy the condition= 0.Finally, We prove that two necessary conditions of tripartite separability for a noisy GHZ-W state are also sufficient for the parameter interval of Θ ∈[0,0.080401π]and[0.080401π,0.11628π] respectively.

ORCID iDs