Nonequilibrium effects of reactive flow based on gas kinetic theory*

Xianli Su and Chuandong Lin

Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519082,China

Abstract How to accurately probe chemically reactive flows with essential thermodynamic nonequilibrium effects is an open issue.Via the Chapman–Enskog analysis, the local nonequilibrium particle velocity distribution function is derived from the gas kinetic theory.It is demonstrated theoretically and numerically that the distribution function depends on the physical quantities and derivatives,and is independent of the chemical reactions directly as the chemical time scale is longer than the molecular relaxation time.Based on the simulation results of the discrete Boltzmann model, the departure between equilibrium and nonequilibrium distribution functions is obtained and analyzed around the detonation wave.In addition,it has been verified for the first time that the kinetic moments calculated by summations of the discrete distribution functions are close to those calculated by integrals of their original forms.

Keywords: discrete Boltzmann method, reactive flow, detonation, nonequilibrium effect

1.Introduction

Chemical reactive flow is a complex physicochemical phenomenon which is ubiquitous in aerospace, energy and power fields,etc[1,2].It exhibits multiscale characteristics in temporal and spatial scales, incorporates various hydrodynamic and thermodynamic nonequilibrium effects [3].The nonequilibrium effects exert significant influences on fluid systems especially in extremely complex environments [3],such as the spacecraft reentry into the atmosphere [4], multicomponent reactive flow in porous media [5, 6], fuel cells[7, 8], phase separation [9], hydrodynamic instability [10],and detonation [11, 12].At present, how to accurately probe,predict and analyze chemical reactive flows with essential nonequilibrium effects is still an open issue.

Actually, there are various classes of methodologies to retain the information of velocity distribution functions for fluid systems.For example, on the basis of the distribution function, Nagnibeda et al established the kinetic theory of transport processes and discussed the features of complex system strongly deviating from the thermal and chemical equilibrium [3].Besides, on the microscopic level, the distribution function can be obtained by using the direct simulation Monte Carlo [13, 14], or molecular dynamics [15, 16].As a kinetic mesoscopic methodology, the discrete Boltzmann method (DBM) is a special discretization of the Boltzmann equation in particle velocity space, and has been successfully developed to recover and probe the velocity distribution functions of nonequilibrium physical systems[11,17–20].

In fact, the DBM is based on statistical physics and regarded as a variant of the traditional lattice Boltzmann method (LBM) [21–24].Compared to standard LBMs, the DBM can address more issues, in particular to simulate the compressible fluid systems with significant nonequilibrium effects [17, 20, 25–30].At present, there are two means to recover the velocity distribution functions.One relies on the analysis of the detailed nonequilibrium physical quantities to obtain the main features of the velocity distribution function in a qualitative way [11, 17, 18].The other is to recover the detailed velocity distribution function by means of macroscopic quantities and their spatio derivatives quantitatively,which can be derived by using the Chapman–Enskog expansion[19,20].The two methods are consistent with each other [20].

In the rest of this paper,we firstly derive the nonequilibrium velocity distribution function of reactive fluid based on the Boltzmann equation in section 2.In section 3, we give a brief introduction of the DBM for compressible reactive flows.In section 4,we verify the consistency of theoretical and numerical results of the equilibrium or nonequilibrium manifestations of reactive flows.The nonequilibrium and equilibrium distribution functions as well as their differences are obtained and analyzed in section 5.Finally, section 6 concludes.

2.Derivation of velocity distribution function of reactive fluid

Now, let us introduce the popular Bhatanger–Gross–Krook(BGK) Boltzmann equation

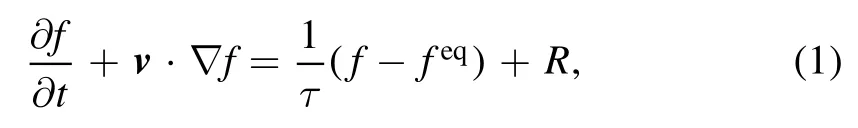
where τ denotes the relaxation time, t the time, f the velocity distribution function.The equilibrium distribution function[31, 32] is

where D=2 denotes the dimensional translational degree of freedom, I stands for extra degrees of freedom due to vibration and/or rotation, and η represents the corresponding vibrational and/or rotational energies.Here n is the particle number density, u the hydrodynamic velocity, T the temperature, m=1 the particle mass, and ρ=nm the mass density.

On the right-hand side of equation (1),R is the chemical term describing the change rate of the distribution function due to chemical reactions, i.e.

To derive the explicit expression of the chemical term, the following qualifications are assumed [26]: tmr＜tcr＜tsys, where tmr, tcrand tsysrepresent the time scale of molecular relaxation,the time scale of chemical reaction and the characteristic time scale of the system, respectively.Under the condition tmr＜tcr,equation (3) can be approximated by

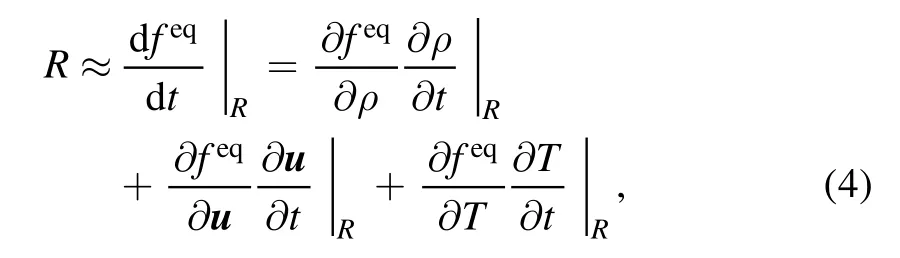
as feqis the function of ρ, u, and T, respectively.Furthermore,the assumption tcr＜tsysleads to the following conclusion: the chemical reaction results in the change of temperature directly,as the density and flow velocity remain unchanged during the rapid reaction process.Consequently, equation (4) can be reduced to

Substituting equation (2) into equation (5) gives

where Q indicates the chemical heat release per unit mass of fuel,λ′ is the change rate of the mass fraction of chemical product.Additionally, a two-step reaction scheme is employed to mimic the essential dynamics of a chain-branching reaction of detonation in this paper [33].

Via the Chapman–Enskog analysis, we derive the firstorder approximation formula of the velocity distribution function of reacting flows through the macroscopic quantities and their spatial and temporal derivatives

in terms of

and

Note that the change rate of temperature consists of two parts,i.e.

on the right-hand side of which the first term describes the part caused by the heat release of chemical reactions

and the other two terms reflect the parts due to the spatial gradients of velocity and temperature.

Therefore, equation (7) can be simplified as

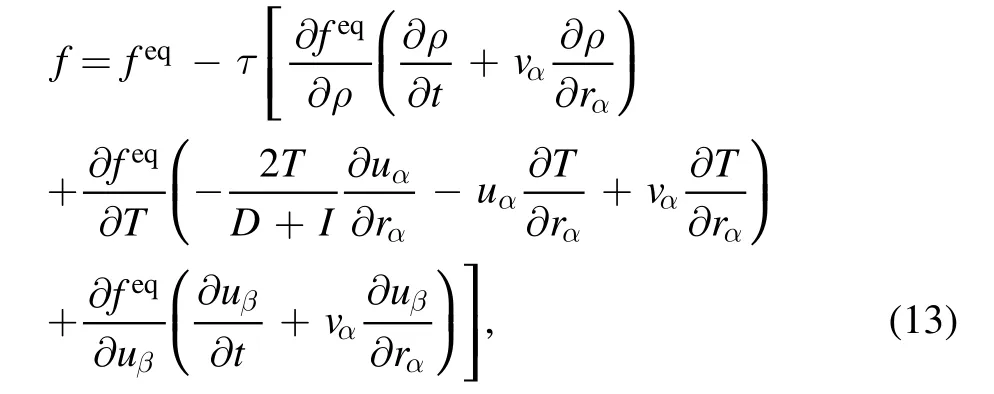
with

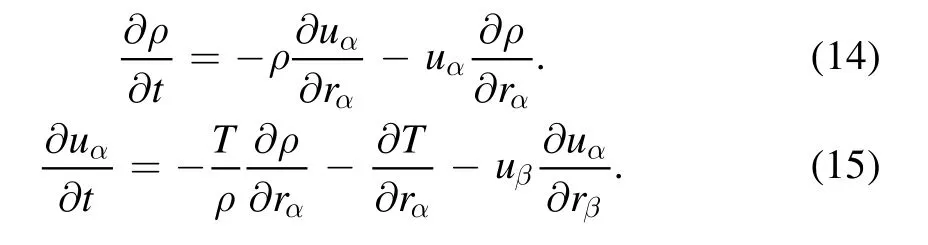
It can be found from equations (11), (12), (14) and (15)that the temporal derivatives can be expressed by the spatial derivatives.Those formulas are obtained from the Chapman–Enskog expansion.In fact,there are two ways to calculate the simulation results ofor.One method is to calculate the temporal change rate directly.For example

The other method is to use equation(11),(14)and(15)where the spatial derivatives can be computed by the finite difference scheme.The results given by the two methods are similar to each other.

Moreover, it can be inferred from equation (13) that the chemical reaction term is eliminated,so it has no contribution to the velocity distribution function directly.This is due to the aforementioned assumption that the chemical time scale is longer than the molecular relaxation time.The case where the chemical time scale is close to or less than the molecular relaxation time is not considered in this work.

3.Discrete Boltzmann method

In this work, the BGK DBM is used to mimic and measure the nonequilibrium reactive flows [34].The discretization of the model in particle velocity space takes the form

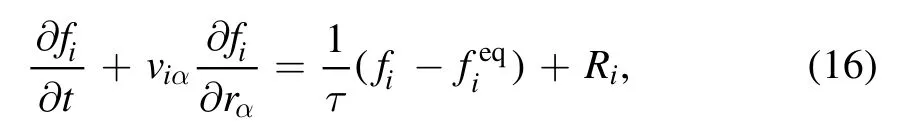
where fiandrepresent the discrete distribution function and its equilibrium counterpart, respectively.videnotes the discrete velocity with i=1,2,3,…,N,and N=16 is the total number of discrete velocities.Here a two-dimensional sixteen-velocity model is employed, see figure 1.

Figure 1.Sketch for the discrete velocity model.

Physically, the DBM is approximately equivalent to a continuous fluid model plus a coarse-grained model for discrete effects.Meanwhile,the DBM is roughly equivalent to a hydrodynamic model plus a coarse-grained model of thermodynamic nonequilibrium behaviors.For the sake of recovering the NS equations in the hydrodynamic limit, the discrete equilibrium distribution functionsare required to satisfy the following relationship

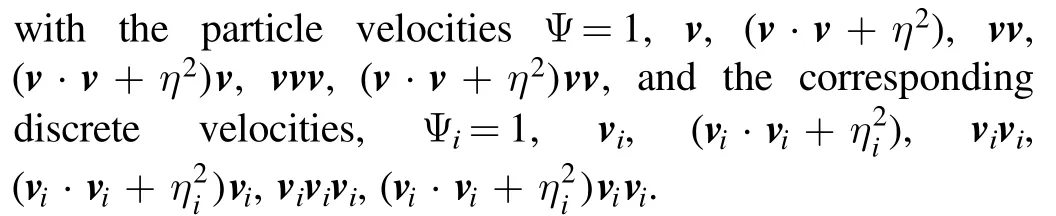
Furthermore, one merit of the DBM is to capture nonequilibrium information described by the following (but not limited to) high-order kinetic moments

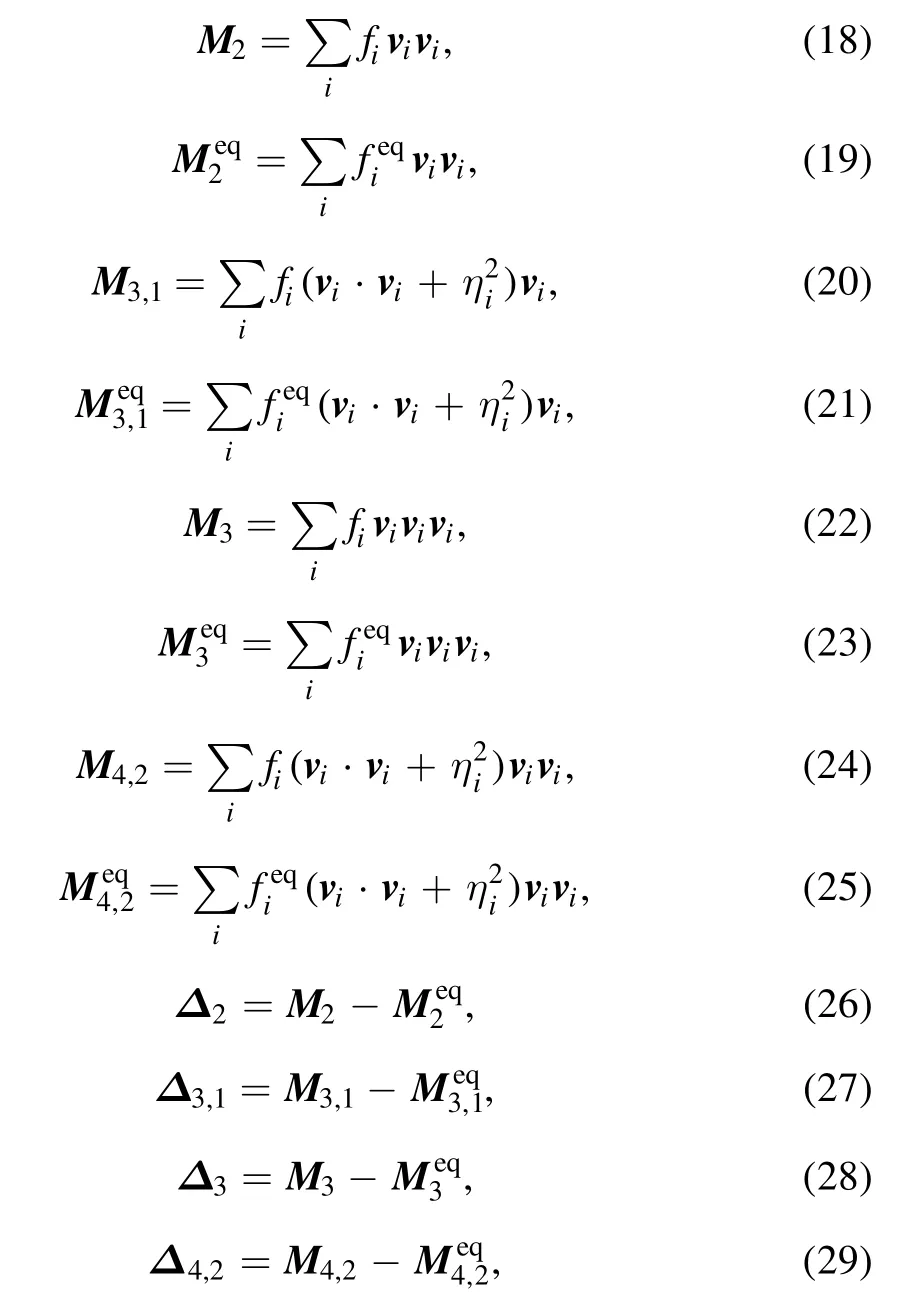
where M2,M3,1, M3and M4,2are the kinetic moments of the distribution functions,anddenote the corresponding equilibrium counterparts, Δ2, Δ3,1, Δ3and Δ4,2are the differences between them.Here, Δ2represents the viscous stress tensor and disorganized momentum flux,Δ3,1and Δ3are relevant to the disorganized energy fluxes.Δ4,2is related to the flux of unnorganized energy flux.

4.Verification and validation

To verify the consistency of theoretical and numerical results of the nonequilibrium manifestations of reactive flows,firstly,we simulate a reaction process in a uniform resting system.The specific-heat ratio is γ=5/3, the chemical heat release Q=1, the space step Δx=Δy=5×10-5, the time step Δt=2×10-6, and the discrete velocities (va, vb, vc, vd, ηa,ηb, ηc, ηd)=(3.7, 3.2, 1.4, 1.4, 2.4, 0, 0, 0), respectively.In order to possess a high computational efficiency, only one mesh grid (Nx×Ny=1×1) is used, and the periodic boundary condition is adopted in each direction, because the physical field is uniformly distributed.It is found that all simulated nonequilibrium physical quantities (including Δ2,Δ3,1, Δ3, and Δ4,2) remain zero during the evolution.Therefore, in the process of the chemical reaction, the deviation of velocity distribution function f from its equilibrium counterpart feqis zero,i.e f=feq.Besides,all physical gradients are zero in the simulation process due to the uniform distribution of physical quantities.Consequently, it is numerically verified that the chemical reaction does not contribute to the nonequilibrium effects directly1It should be mentioned that the chemical reaction may change the physical gradients which make an impact on the nonequilibrium effects.In other words,the chemical reaction plays an indirect role in nonequilibrium effect of the reactive flows..This result is consistent with the aforementioned theory that the distribution function depends on the physical quantities and derivatives,and is independent of chemical reactions directly,see equation (13).

For the purpose of further validation, the one-dimensional (1D) steady detonation is simulated.The initial configuration, obtained from the Hugoniot relation, takes the form

where the subscript L indicates 0 ≤x ≤0.00555, and R indicates 0.00555 ＜x ≤0.555.The Mach number is 1.96.To ensure the resolution is high enough, the grid is chosen as Nx×Ny=11 100×1, other parameters are the same as before.Furthermore, the inflow and/or outflow boundary conditions are employed in the x direction, and the periodic boundary condition is adopted in the y direction.

Figure 2 displays the kinetic moments of velocity distribution function (M2,xx, M2,xy, M2,yy, M3,1,x, M3,1,y), the equilibrium counterpartsand the nonequilibrium quantities (Δ2,xx, Δ2,xy, Δ2,yy, Δ3,1,x,Δ3,1,y) around the detonation front.Here Δ2,xxrepresents twice the disorganized energy in the x degree of freedom,and Δ2,yytwice the disorganized energy in the y degree of freedom.Δ3,1,xand Δ3,1,ydenote twice the disorganized energy fluxes in the x and y directions, respectively.The legends are in each plot, where the dashed line is located at the position x=0.50375.

Next, let us verify that the kinetic moments calculated by the summations of the discrete distribution functions are close to those calculated by integrals of their original forms at the location x=0.50375.The kinetic moments calculated by the summations of the discrete distribution functions are (Δ2,xx, Δ2,xy,Δ2,yy, Δ3,1,x, Δ3,1,y) = (0.48449, 0, -0.35844, 2.891 23, 0),while the results of the corresponding integration counterparts are(Δ2,xx,Δ2,xy,Δ2,yy,Δ3,1,x,Δ3,1,y)=(0.56488,0,-0.27255,2.801 81, 0).The relative errors are (17%, 0%, 24%, 3%, 0%),which is roughly satisfactory.For the first time, this test demonstrates the accuracy of the nonequilibrium manifestations measured by the DBM, and validates the consistence of the DBM with its theoretical basis.

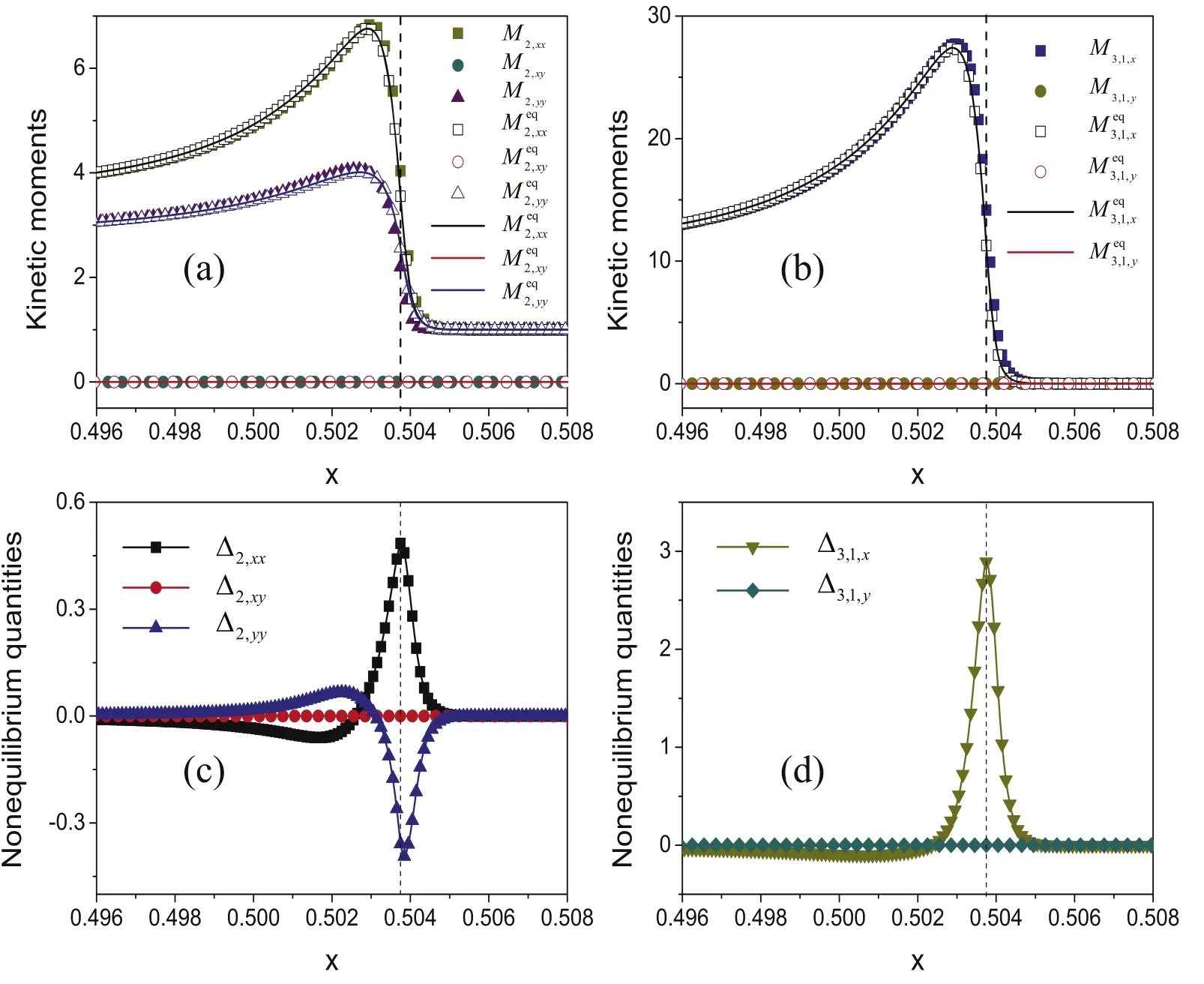
Figure 2.The nonequilibrium and equilibrium kinetic moments, and the differences between them.Plots (a)–(d) show the independent variables of M2 (, M3,1 Δ2, and Δ3,1, respectively.

5.Recovery of velocity distribution function around detonation wave

To further perform a quantitative study of the nonequilibrium state around the detonation wave, figure 3(a) displays the velocity distribution function at the peak of Δ2,xx,which is on the vertical dashed line in figure 2.It is clear that the velocity distribution function has a peak in the two-dimensional velocity space.Actually, due to the nonequilibrium effects,the velocity distribution function deviates from its local equilibrium counterpart, i.e.the Maxwellian velocity distribution function.

In order to have an intuitive study of the local velocity distribution function, figure 3(b) shows its contours in the velocity space, which is in line with figure 3(a).Clearly, the peak is asymmetric in the vxdirection and symmetric in the vydirection.The contour lines are close to each other near the peak (especially on the left side), and becomes sparse away from the peak(especially on the right side).That is to say,the gradient is sharp near the peak (especially on the left side),and smooth far from the peak (especially on the left side).

To have a deep understanding of the deviation of the velocity distribution function from the equilibrium state,figure 3(c) depicts the difference between the nonequilibrium and equilibrium distribution functions in the two-dimensional velocity space.It is obvious that there are both positive and negative deviations around the detonation wave.Along the vxdirection, a high positive peak first appears, then decreases to form a valley, and then increases to a low positive peak.

As can be seen in figure 3(d), the deviation is symmetric about vy=0, and asymmetric about vx=ux.The contour plot consists of three segments along the vxdirection.The leftmost segment is in the region of the first peak, where the contour lines are approximately elliptical.The middle part is in the low valley area that seems like a‘moon’ shape.And the rightmost one is in the low peak area, which likes a ‘cobblestone’.The contour lines between the high peak and the valley are closer to each other than those between the valley and low peak,because the gradients between the leftmost and middle parts are sharp than those between the middle and rightmost regions.

Finally, let us investigate the one-dimensional distribution functions and the corresponding deviations from the equilibrium states.Figures 4(a) and (b) depict the velocity distribution functions in the vxand vydirections,respectively.The solid lines represent the velocity distribution functions f(vx)=∫∫fdvydη and f(vy)=∫∫fdvxdη, the dashed curves express the equilibrium counterparts feq(vx)=∫∫feqdvydη and feq(vy)=∫∫feqdvxdη, respectively.Figures 4(c) and (d) show fneq(vx)=f(vx)-feq(vx) and fneq(vy)=f(vy)-feq(vy) which indicate the departures of distribution functions from the equilibrium state in the vxand vydirections,respectively.The following points can be obtained.

(I) In figures 4(a)–(b), there is a peak for each curve of f(vx),feq(vx),f(vy),and feq(vy).In figures 4(c)–(d),there are two peaks and a trough for fneq(vx), while a peak and two troughs for fneq(vy).Along the vxdirection,fneq(vx) forms a positive peak firstly, then decreases to form a valley, and then increases to a second positive peak.Because f(vx)is first greater than feq(vx),then less than feq(vx), and finally greater than feq(vx) again.Similarly, the relation f(vy)＞feq(vy) or f(vy)＜feq(vy)in figure 4(b) leads to the results fneq(vy)＞0 or fneq(vy)＜0 in figure 4(d).

(II) f(vx) and fneq(vx) are asymmetric about the vertical dashed line located at vx=ux, while feq(vx) is symmetric.Physically, as the detonation evolves, the compressible effect plays a significant role in the front of the detonation wave,and the internal energy in the x degree of freedom increases faster than in other degrees of freedom, and there exists disorganized heat flux in the x direction.

(III) In figures 4(b) and (d), each curve of f(vy), feq(vy) and fneq(vy) has a positive peak which is symmetric about vy=0.On the left and right parts of fneq(vy) are two identical troughs that are symmetrically distributed in figure 4(b).Because the periodic boundary condition is imposed on the y direction, the equilibrium and nonequilibrium velocity distributions for vy＞0 and vy＜0 are symmetrical.

Figure 3.The velocity distribution function(a)and its corresponding contour(b),the deviation of the velocity distribution function from the equilibrium state (c) and its corresponding contour (d).

Figure 4.One-dimensional nonequilibrium and equilibrium distribution functions in the vx (a) and vy (b) directions, and the differences between them in the vx (c) and vy (d) directions.

(IV) The nonequilibrium manifestations in figures 2(a)–(d)are consistent with the deviations of distribution functions in figures 4(a)–(d).Specifically, the trend of fneq(vx) indicates that f(vx) is ‘fatter’ and ‘lower’ than feq(vx), which means the disorganized momentum flux Δ2,xx＞0.The trend of fneq(vy) means that f(vy) is‘thinner’ and ‘higher’ than feq(vy), which indicates Δ2,yy＜0.Meanwhile, the portion f(vx＞ux) is ‘fatter’than the part f(vx＜ux), which is named ‘positive skewness’ and indicates Δ3,1,x＞0.And the symmetry of fneq(vy) means Δ3,1,y=0.

6.Conclusions

Via the Chapman–Enskog expansion,the velocity distribution function of compressible reactive flows is expressed by using the macroscopic quantities and their spatial derivatives.The equilibrium and nonequilibrium distribution functions in oneand two-dimensional velocity spaces are recovered quantitatively from the physical quantities of the DBM, which is an accurate and efficient gas kinetic method.The departure between the equilibrium and nonequilibrium distribution functions is in line with the nonequilibrium quantities measured by the DBM.Moreover, it is for the first time to verify that the kinetic moments measured by summations of the distribution function resemble those assessed by integrals of the original forms,which consists with the theoretical basis of the DBM.In addition, under the condition that the chemical time scale is longer than the molecular relaxation time, it is numerically and theoretically demonstrated that the chemical reaction imposes no direct impact on the thermodynamic nonequilibrium effects.