Thermal currents obtained and mutually switched by a modified Haldane model in graphene

Xiao-Long Lü and Hang Xie

1 College of Science, Guangxi University of Science and Technology, Liuzhou 545006, China

2 College of Physics, Chongqing University, Chongqing 400000, China

3 Chongqing Key Laboratory for Strongly-Coupled Physics, Chongqing University, Chongqing 400000,China

Abstract By using the transfer matrix method,we discover three types of current,such as the 100%spinvalley polarized current, pure spin-valley current and pure charge current, in a two-terminal graphene system.These types of current can be obtained and mutually switched by modulating the parameters of the modified Haldane model (MHM).In our work, these types of current are driven by the thermal bias.Compared with this method of increasing the one-lead temperature(with a fixed temperature difference),the thermal currents can be more effectively strengthened by increasing the temperature difference(with a fixed one-lead temperature).In order to rapidly turn off these currents,we choose to enhance the intensity of the off-resonant circularly polarized light instead of canceling the temperature difference.These results indicate that the graphene system with the MHM has promising applications in the spin and valley caloritronics.

Keywords: graphene, modified Haldane model, thermal currents

1.Introduction

Due to the valley degree of freedom in addition to the charge and spin of an electron, novel valleytronics that can store,manipulate and encode information rises.In two-dimensional materials, two inequivalent valleys origin from the maximum(minimum) of valence (conduction) band in the first Brillouin zone [1–9].And the valley degree of freedom has been experimentally realized by the means,such as electric,magnetic and optical fields [10–12], which is an important platform to design valleytronics.In graphene, the valley polarized transport is theoretically proposed by the strain and magnetic field[13–16].In recent years, valleytronics has been applied in the caloritronics called as the valley caloritronics using the thermoelectric heat to drive the valley current[17–20].Based on the valley caloritronics,some related valley phenomena appear.For instance, the valley Seebeck effect is proposed by breaking the transmission symmetry around zero energy in the first subband of the zigzag graphene nanoribbon [20]; and the valley-locked spin-dependent Seebeck effect is discovered with a proximityinduced asymmetric magnetic field [17].

Haldane first introduced the Haldane model to realize the quantum anomalous Hall effect in the absence of external magnetic field [21], and the experimental realization of the Haldane model is first achieved by using cold atoms in a shaken optical lattice [22].The means, such as Fe-based honeycomb ferromagnetic insulator[23]and transition-metal pnictides[24],are also proposed to realize the Haldane model.Based on the Haldane model,Colomés and Franz have theoretically proposed the modified Haldane model revealing the antichiral edge modes,where two copropagating edge modes are compensated by the bulk counterpropagating modes.Actually, the modified Haldane model might be possible with Weyl semimetals and transition metal dichalcogenides monolayers [2, 25–28].The modified Haldane model has been used in some applications.For instance,Marc Vila obtained a rich phase diagram of optical absorption with a modified Haldane model [28], and Marwa Mannaï and Sonia Haddad obtained a strain-tunable edge current in topological insulator with a modified Haldane model[29].

2.Model and methods

In figure 1,we theoretically propose a two-terminal graphenebased system to design three types of current.Before introducing the results, we define the direction of the current propagating from the left thermoelectrode (region I) to the right thermoelectrode (region IV)as the positive direction.In the region II called as a valley chooser, we consider a modified Haldane model and staggered potential, while in the region III called as a spin chooser, the staggered exchange interaction and off-resonant circularly polarized light are considered.Near two momentum valleysKandK′, the lowenergy effective Hamiltonian can be expressed as

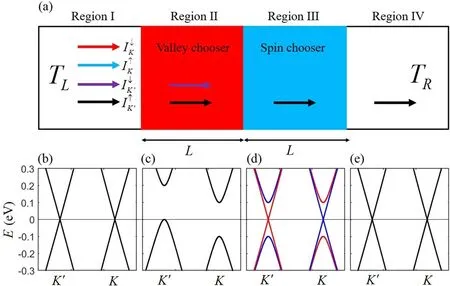
Figure 1.(a)Schematic illustration of a two-terminal graphene-based system with left and right thermoelectrodes that have a kinetic energy difference Δω = kB TL - kB TR = 0.005 eV,the widths of regions II and III are set as L.The energy bands in figures (b)–(e) correspond to regions I–IV,respectively.In the energy bands,the red and blue lines denote the spin-up and spin-down modes,respectively,and the black line denotes the degeneracy of the spin.In the region II, φ= 5 π/6,t 2 = 90 eV and Δ = 0.1 eV.In region III, λ Ω=0.05 eV and λ AF = 0.05 eV.In regions I and IV, no external fields exist.

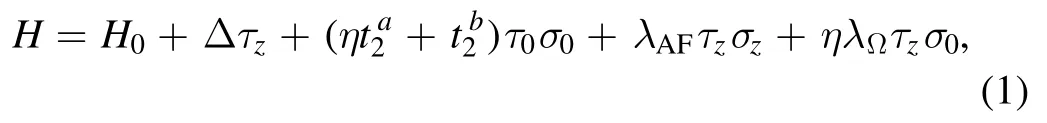
where the first termH0=ħvF(ητxkx+τy ky)denotes pure graphene interactions in regions I and IV without external fields.vF= 1 × 106m s-1represents the Fermi velocity andħ is the reduced Plank constant.η= ±1 correspond to the valleysKandK′,τiandσiwith the indexi=x,y,zdescribe the sublattice and spin Pauli matrices,respectively.Besides,0τand0σare the corresponding unit Pauli matrices.The second term denotes the staggered potential,which can be obtained by putting the graphene-based model on an h-BN substrate[30, 31], the third term denotes the modified Haldane model,wherecosφ.In addition,some possible schemes have been proposed to obtain the modified Haldane model in graphene[25,28].The fourth term represents the staggered exchange interaction, which can be hardly realized in planar structure such as graphene.We proposed an appropriate method that depend on the bulk or planar structure to induced staggered interaction.Based on the ab initio calculations [32], the exchange interaction and staggered potential emerge as the graphene is put on the hexagonal BN planar deposited on ferromagnetic Co or Ni[33]or the hBN/(Co,Ni)[34].For the purpose of obtaining the exchange interaction,one can use the staggered potential of the second term of equation (1) to balance the induced staggered potential by the ferromagnetic proximity.And the exchange interaction can be expressed aswhereandare the exchange interaction at the sublattices A and B,respectively.In a special case ofthe fourth term appears.The fifth term arises from the case, where a beam of off-resonant circularly polarized light ofA(t) =A[ξsin (ωt)ex+cos (ωt)ey]is coupled to the graphene-based model [35–37].AndλΩ=ξ(eAvF)2/ħω,whereξ= ±1 represent the right and left polarized light.The basis of the Hamiltonian equation(1)is presented in detail in the appendix A.

From the Hamiltonian (1), we can easily obtain the eigenvalues

where the signs ± denote the conduction and valence bands, respectively.The variableS= ±1 are defined for the spin-up and spin-down modes, respectively.Based on the equation (2), the corresponding wave function with a given energyEcan be derived as

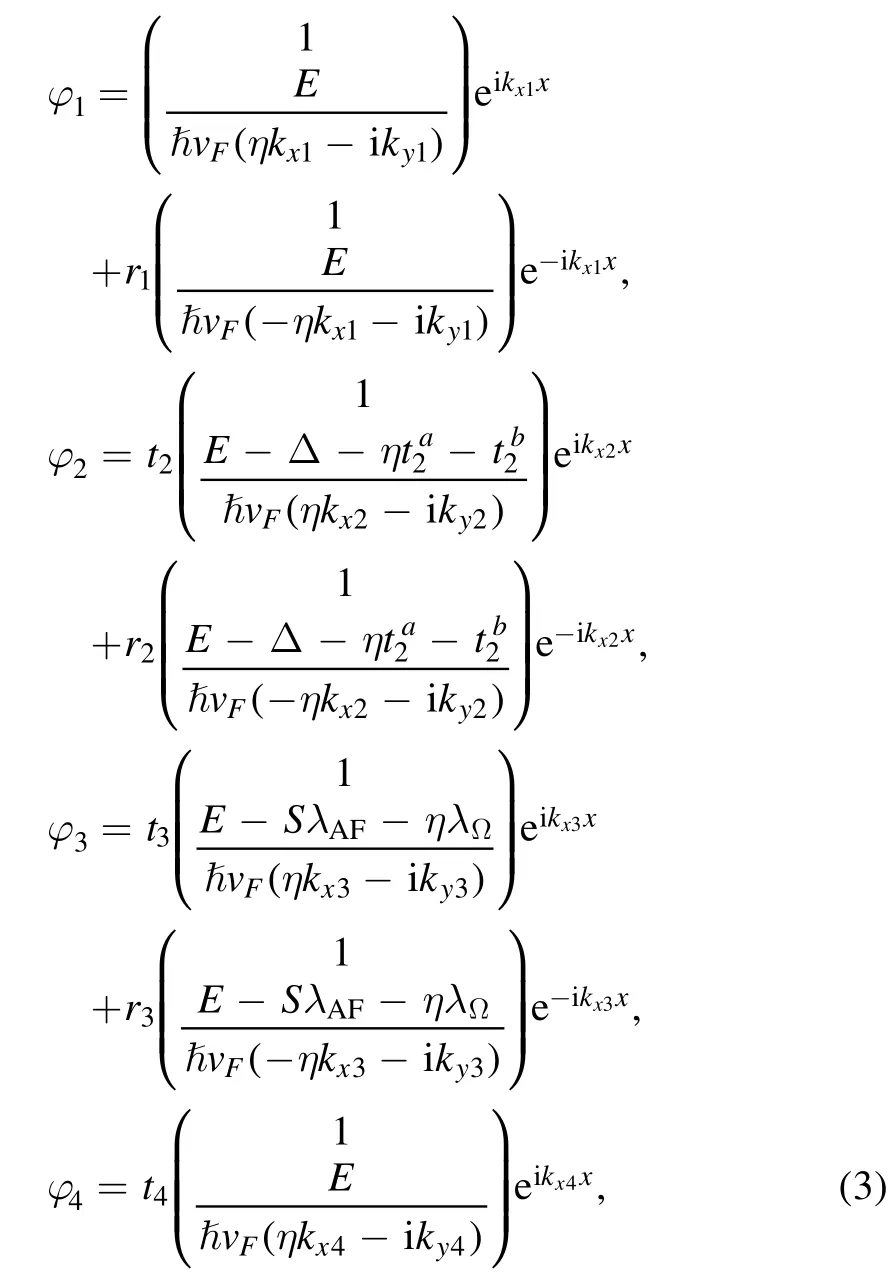
where the indicesi=1, 2, 3, 4of the wave functionφirepresent the regions I–IV, respectively.In the same case,the indicestiandridenote the transmission and reflection coefficients in the corresponding regions, respectively.In addition,kxiandkyiare the wavevectors.

Here, we use the transfer matrix method to obtain the total transmission.By using the continuity condition of the wave functions at each interface between nearest regions, we can get simple formulas at each interface as

10. Husband: The father/husband s role in the tale is an interesting one. While the father is usually the birth father of the children, he has different levels of responsibility for the abandonment across versions of the tale. In some versions he willingly leaves the children in the forest. In other versions, he ineffectively protests their abandonment. The textual hint that the wife s wishes will win over the children s safety comes from the word choice of husband over father to describe the man s primary role.Return to place in story.

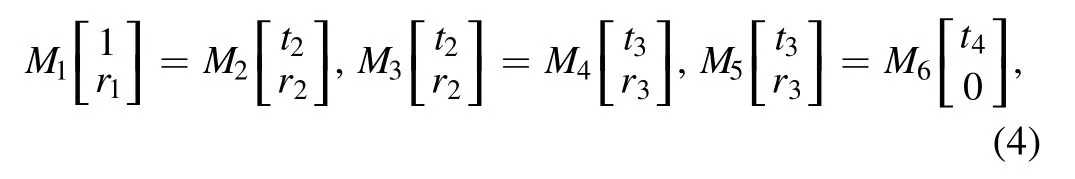
where the matricesMiare expressed as

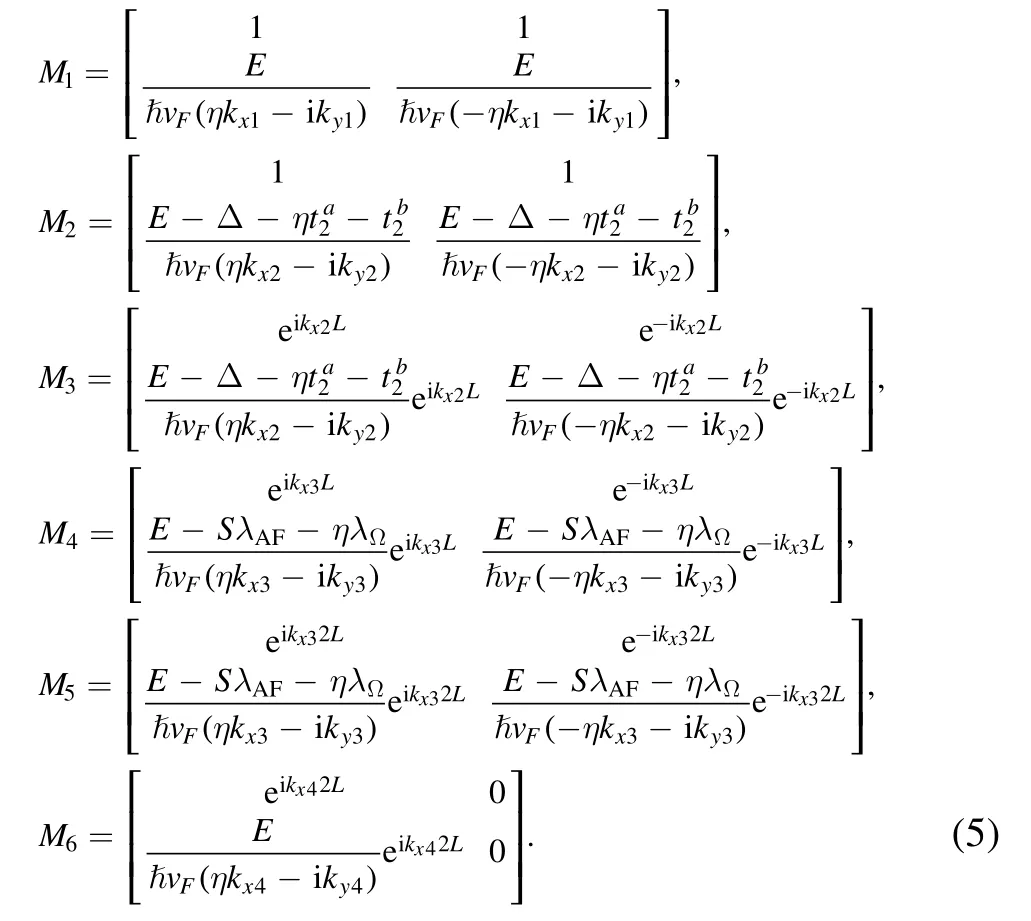
It is obvious that the rearranged formula for the equation (4)can be reduced as

with the total transfer matrix[38].Then, the transmission coefficient is easily derived aswhereM11is the element of the total transfer matrixM.The spin-valley dependent transmission probability is also easily obtained as

this formula is suitable for the case, where the left and right thermoelectrodes are symmetrical.In addition, another method for calculating the transmission coefficientt4is presented in the appendix B.Furthermore, the total spin-valley transmission probability with incident angleθis expressed as

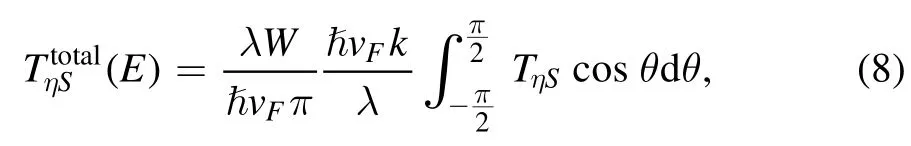
with large enough widthWof graphene-based system.We introduce the energy scaleλ= 0.0039 eV to make these termsλW/ħvFπand ħvFk/λdimensionless.In addition, this term ħvFk/λis dimensionless variable due to the wavevectork.And the incident angleθsatisfies the condition ofθ=arctan (k y1/kx1) .After obtaining the total transmission probability, one can get the formula of the spin-valley current by using the generalized Landauer–Büttiker transport approach as

3.Results and discussion

As we know,the size effect has an important influence on the transport property, which can be ignored by choosing an appropriate size.Before analyzing three types of current arising from a temperature difference, the effect of different widths of the regions II and III on the transport property has been discussed below.According to equation (8), the total spin-valley transmission can be calculated easily, which corresponds to the model shown in figure 1.From figures 2(a)–(d),it reveals that the gaps of those transmissions tend to be a steady region with the increasing widths of the regions II and III.We find that the total transmission gaps in figure 2(d) are well consistent with the energy band gaps in figures 1(b)–(d)as the length exceeds a certain value,such asL= 150a.Therefore, we choose the appropriate length asL=150ato calculate the transport property in the following.Besides, all these total transmissions are based on the model in figure 1.

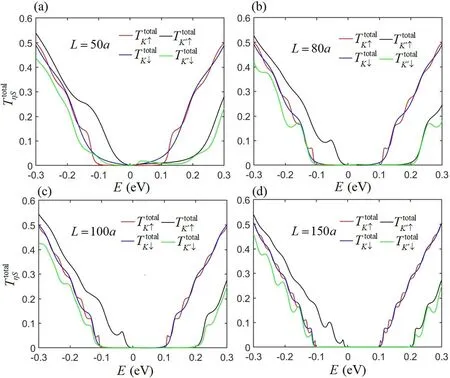
Figure 2.Transmissions with different width L of regions II and III, a is the lattice constant of graphene.

In figure 1(a),we modulate the phaseφof the modified Haldane model in the region II to obtain 100% spin-valley polarized current (SVPC) shown in figures 3(e) and (f),which can be used as a spin-valley filter.Before we give a detailed discussion on the 100%SVPC,the character of the Fermi function should be simply described.According to the calculation of the Fermi function, the states can be excited about the region of -7kBT≤E-Ef≤7kBTby the temperature, which is important for explaining the results in the following.In the region of0 ≤k B TR≤0.01 eV,there exist the spin and valley currents, while the absolute values of the spin and valley polarizations are both 1,which is called as 100% SVPC shown in figure 3(e).We can use the induced formularewritten from equation (9) to explain these phenomena.In the region of0 ≤kBTR＜0.01 eV,the states can be excited for the region of -7kBTL＜E-Ef＜7kBTL(-0 .102 eV ＜E-Ef＜ 0.102 eV) .In figures 1(d)and 3(a),it is clearly shown that the Fermi function difference for the spin-up mode with the valleyK′ satisfeis the case, where Δf＜ 0under0 ＜E＜ 0.102 eV due to the excited states and Δf= 0underE≥ 0.2 eV orE≤0.102 eV due to no excited states.Moreover, the total transmission also satisfies the case, whereunder0 ≤E≤ 0.2 eV due to the gap effect andunderE＜0 due to the specific spin-matching tunneling.Thus, the currentis opposite according to the reduced formulaAtkBTR= 0.01 eV,a little state with spin-down mode can be excited in the valleyK′ as a result of that the excited state region of -0.102 eV ≤E-Ef≤ 0.102 eV exceeds the boundary of the gap of[- 0.1 eV, 0.2 eV] .And the currents with the valleyKare also zeros as a result of the symmetric bands in the valleyK[9].Thus,the valley currentJVis positive and the spin currentJSis negative in the region ofkB TR≤ 0.01 eV.Meanwhile, the value ofPSis almost 0.99,which can be regarded as a critical value of the 100%SVPC.In the region ofkBTR＞ 0.01 eV,the currentemerges due to the larger temperature broadening.Therefore, the value of the spin polarization is obviously less than 1,while the value of the valley polarization is not changed.Compared with the case in figure 3(c), the spin and valley currents are strengthened as a function of the kinetic energy differenceΔωshown in figure 3(d),which is also called as 100%SVPC in the region of 0 ＜Δω≤ 0.011 eV.At Δω= 0.011 eV,a little state with the spin-up mode can be excited in the valleyK′, but the error of the valley polarization is inside 1%from 1,which is safe to be called as the 100% SVPC.

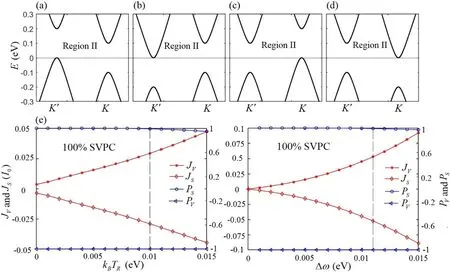
Figure 3.Band structures in region II shown in figure 1(a)and the corresponding quantities JS , JV ,PS and PV .(a) φ= 5 π / 6,(b) φ =π / 6,(c)φ= -5 π/ 6,(d) φ= -π / 6.(e)The quantities JS , JV ,PS and PV as a function of kB TRwith respect to the band structure(a).(f)The quantities JS , JV ,PS and PV as a function of Δω with a fixed k B TR = 0.005 eV with respect to the band structure (a).

In the region II,we modulate the phase asφ=π/ 6instead ofφ= 5π/ 6,and the corresponding band structure shown in fgiure 3(b) implies that the direction of the 100% SVPC is opposite, which can fliter the spin-up current with the valleyK′.The phaseφis further modulated as -5π/6shown in fgiure 3(c),which means the 100% SVPC can fliter the spin-down current with the valleyK.And the direction of this current can be opposite by modulating the phase asφ= -π/ 6shown in fgiure 3(d).In the region III shown in fgiure 1(a), when we modulate the polarized direction of the light from the right to the left, the bands in the valleysKandK′ shown in fgiure 1(d) are interchanged not shown here.Therefore, the 100% SVPC can also fliter the spin-up current with the valleyKand the spin-down current with the valleyK′.

We modulate the phase asφ= -π/ 2shown in figure 4(c),the direction of the pure SVC can be opposite not shown here.In the region III shown in figure 1(a), we also modulate the polarized direction of the light from the right to the left, so that a spin chooser selects different spin modes in the same valley.Then, another two forms of the pure SVC emerge not shown here.

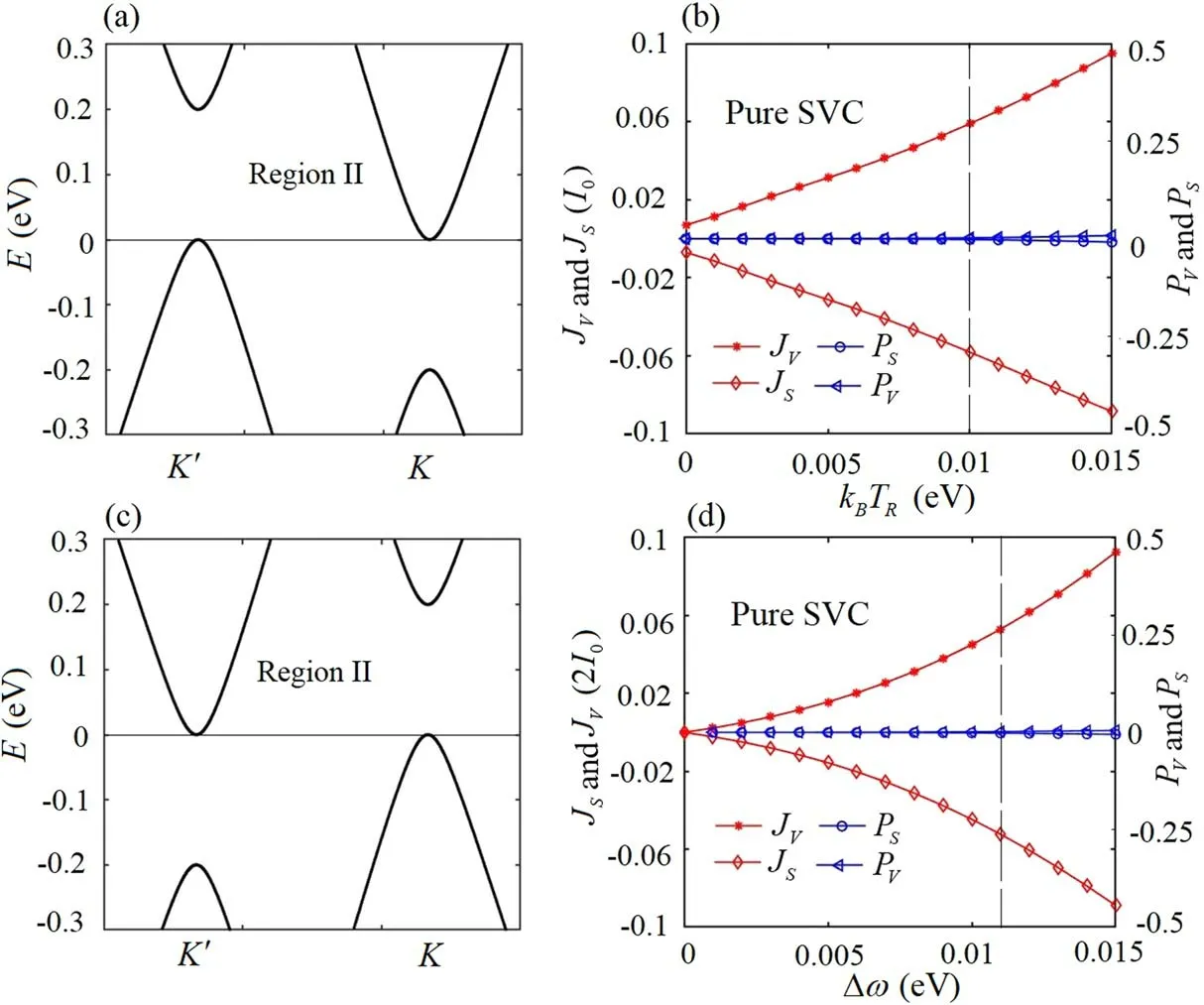
Figure 4.Band structures and the corresponding quantities JS , JV ,PS and PV .(a) φ =π / 2,(b)The quantities JS , JV ,PS and PV as a function of k B TRwith respect to the band structure (a), (c) φ= -π/ 2.(d) The quantities JS , JV ,PS and PV as a function of Δω with a fixed k B TR = 0.005 eV with respect to the band structure (c).

We further modulate the phase asφ= ±πand next-nearneighbor hopping ast2= 1 /3 0 eV in the region II, then the pure SVC can be switched into the pure charge current(CC) shown in figures 5(b) and (d).In figures 5(a) and 1(d),there exist four gaps for four types of the bands, such as[0 , 0.2 eV] , [0 , 0.2 eV] , [- 0.1 eV, 0.2 eV]and[-0.1 eV, 0.2 eV] .It is shown that atkB TR= 0.01 eV the currentsandcan contribute to the transport due to the larger temperature broadening.In figure 5(b),the values ofPVandPSare almost 0.002 atkB TR= 0.01 eV,which can be regarded as a critical value of the pure CC.Compared with the case in figure 5(b), the pure CC can be strengthened by increasing the kinetic energy differenceΔωshown in figure 5(d).The values ofPVandPSare also 0.002 at Δω= 0.011 eV,which can be regarded as a critical value of the pure CC.We also modulate the phase asφ=0 shown in figure 5(c),corresponding to the opposite direction of the pure CC shown in figure 5(b).

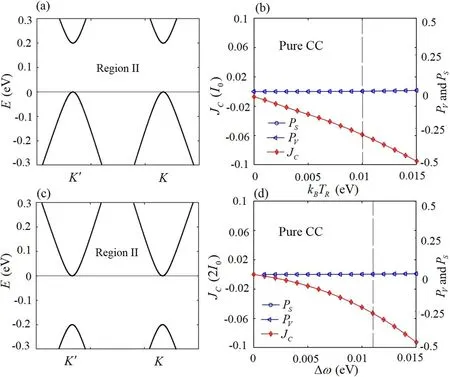
Figure 5.Band structures and the corresponding quantities JS , JV ,PS and PV .(a)φ= ± πandt2 = 1 /3 0 eV.(b)The quantities JS , JV ,PS and PV as a function of k B TRwith respect to the band structure(a),(c)φ = 0andt 2 = 1 /3 0 eV.(d)The quantities JS , JV ,PS and PV as a function of Δω with a fixed k B TR = 0.005 eV with respect to the band structure (c).

Here, we just pay attention to the off-on state of these types of current, such as the 100% SVPC, pure SVC and pure CC.It is required a long time to turn off the states by canceling the kinetic energy difference [39–41],which is a low efficiency.We find that these types of the current can be turned off by the off-resonant circularly polarized light.The currentsJαin figures 6(a)–(c) correspond to the cases in figures 3(a)–5(a), respectively.In figure 6, the off states are in the region of∣λΩ∣ ≥0.12 eV as a result of that the excited state region of-7kBTL＜E-Ef＜ 7kBTL(- 0 .07 eV ＜E-Ef＜0.07 eV)is inside four gaps such asAnd the critical valueλΩof the off state satisfies the simple formulaλΩ=λAF+7kBTL.

Figure 6.Currents Jα as a function ofλΩ with a fixed k B TL = 0.01 eV and kB TR = 0.005 eV (a) corresponds to the case in figures 2(a), (b)corresponds to the case in figures 3(a), (c) corresponds to the case in figure 4(a).

4.Conclusion

In summary, we propose a two-terminal graphene-based system with four regions to generate three types of thermoelectric current.And these currents stem from the functions of a valley chooser and spin chooser,as well as the temperature difference.By just modulating the modified Haldane model in the region II while other parameters are kept unchanged,these types of current can be obtained and mutually switched.Moreover, the on states can be efficiently turned off by increasing the circularly polarized light intensity.

Acknowledgments

This work was supported by the starting foundation of Guangxi University of Science and Technology (Grants No.21Z52).The support from the National Natural Science Foundation of China(No.11847301)and the Natural Science Foundation of Chongqing (No.cstc2020jcyj-msxmX0860)are also appreciated.

Appendix A

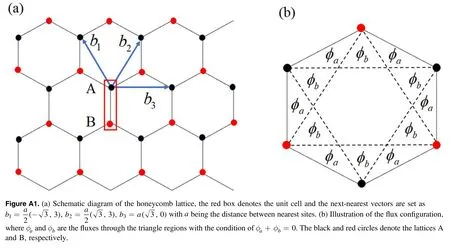
Without the off-resonant circularly polarized light, the tightbinding model of graphene can be written as:

whereξ= ±1 denote the right and left polarized direction of the light, respectively.In the limit ofA2≪1,the effective Floquet Hamiltonian equation(A3)is approximately expressed as

Appendix B

The wave functions in corresponding regions in equation (3)can be rewritten as

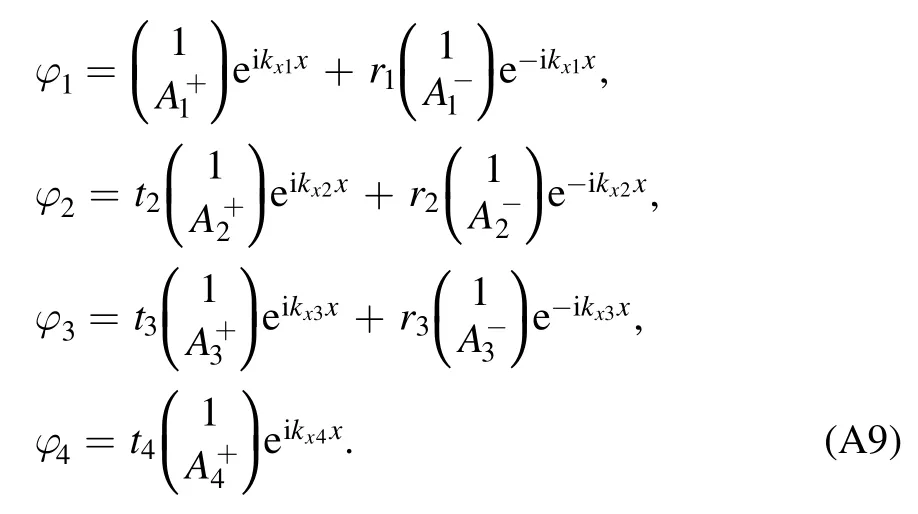
According to the continuity of the wave functions at each interface between nearest regions, we can get a series of equations in the following

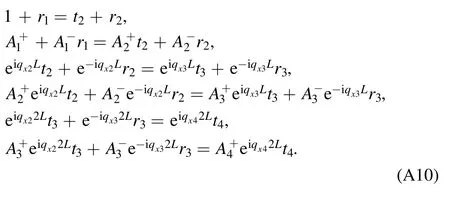
In the matrix form, equation (A10) can be rewritten as

where

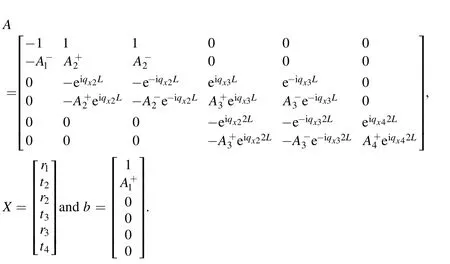
To avoid inverting the matrixAfor calculating the transmitted coefficientt4, we choose the Cramer’s Rule.Then,the transmitted coefficientt4can be obtained by this formula

where

Compared with the Cramer’s Rule, the transfer matrix method can easily handle large number of the scattering regions in the heterojunction system.