计及运行风险与韧性的综合能源系统薄弱环节辨识

2022-03-23陈丽娟许晓慧

电力系统自动化 2022年6期

陈丽娟，刘丽，周昶，许晓慧

（1. 东南大学电气工程学院,江苏省南京市 210096；2. 中国电力科学研究院有限公司（南京）,江苏省南京市 210003）

0 引言

在环境问题和气候危机的影响下,中国提出了“碳达峰、碳中和”目标,致力于推动能源绿色化、低碳化发展,在此背景下,有必要发展融合多种新型清洁能源的综合能源系统（integrated energy system,IES）［1-4］。然而,IES 在运行过程中面临多种不确定性因素,当存在新能源出力及负荷随机波动或随机故障扰动时,需要建立评估指标综合反映IES 运行安全性水平［5］。

目前,针对电网的风险评估［6］发展较为迅速。在电力系统风险评估方法方面,用于刻画不确定性因素对电网影响的概率潮流［7-10］应用较为广泛。文献［11］考虑了风电波动,利用概率潮流获取电压的概率密度并评估了电网风险。文献［12］采用基于场景削减的概率潮流方法,从电压、网损、支路潮流三方面评估电网运行风险。但是,上述风险评估研究均局限于单一电网,尚未扩展到多能流耦合的IES。对于IES 的运行风险研究,目前主要着重于可靠性评估。文献［13］基于状态抽样建立了电-热互联IES 的可靠性评估模型。文献［14］通过马尔可夫链评估IES 的可靠性。然而,上述评估的模拟周期通常是较长的时间段（如1 a）,同时需要多次反复模拟以满足收敛性要求［13］,仿真时间较长且只能得到平均概念上的可靠性指标。这种评估方法不适用于短时间尺度的运行层面,只适用于长时间尺度的规划层面。上述可靠性研究均基于确定性IES 模型,未考虑到源荷随机性的影响。因此,需要从运行层面考虑不确定性因素构建能够指导在线运行的IES风险评估方法。

以上研究内容是针对正常运行时面向风、光、荷随机波动的风险分析,这些扰动往往发生概率高但严重度低,而发生概率低但高严重度的极端事件下的随机故障也是影响IES 安全性的一个重要因素,在评估中也是需要考虑的［15］。针对极端事件,文献［16］考虑了台风天气下的故障,定义了电力系统韧性指标,评估故障下的系统性能。文献［17］基于韧性梯形曲线量化了故障带来的影响。电力系统韧性用于描述极端事件下故障发生前、中、后系统的性能［18］。目前,韧性研究大多集中于电力系统,需要将韧性的概念扩展至IES 层面,实现极端事件下的安全性分析。同时,将其与正常态下的风险指标相结合,通过综合指标判断系统的薄弱环节。

针对以上问题,本文开展了计及运行风险和韧性的IES 薄弱环节辨识研究。基于半不变量法概率多能流建立了风险评估模型,实现风险的快速分析。针对极端事件提出了IES 运行韧性评估方法,并将概率多能流与韧性优化计算相结合,提出了IES 的薄弱环节辨识方法。

1 电-热-气互联IES 稳态多能流

对IES 进行考虑多种不确定性因素的运行风险评估,需要分析IES 的随机性多能流,随机性能量流的计算基于如下的确定性稳态能量流模型。

1.1 电力系统数学模型

电力系统数学模型的极坐标形式潮流方程［18］为：

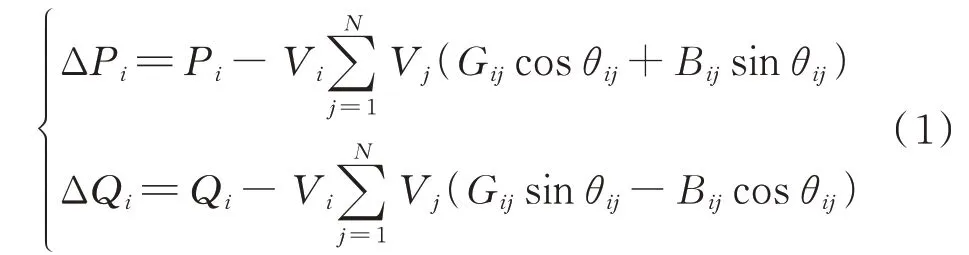
式中：ΔPi和ΔQi分别为节点i注入的有功和无功功率的不平衡量；Pi和Qi分别为节点i注入的有功和无功功率；Vi为节点i的电压幅值；θij为节点i和节点j之间的电压相角之差；Gij和Bij分别为节点i和节点j之间的电导和电纳；N为节点总数。

1.2 热力系统数学模型

热网供回水管道数学模型包括水力和热力模型方程［19］,表达式为：

式中：A为节点-管道关联矩阵；B为回路-管道关联矩阵；hf为压头损失矩阵；K为阻力系数矩阵；m为管道流量矩阵；mq为节点负荷流量矩阵；Φ、Cp、Ts和To分别为节点热功率矩阵、比热容、供水温度矩阵和出口温度矩阵；Tend、Tstart、Ta、λ和L分别为管道末节点温度矩阵、管道首节点温度矩阵、环境温度矩阵、导热系数和管道长度矩阵；Λout和Λin分别为流出和流入节点的流量集合；TW为水流流入温度集合；mout和min分别为流出和流入管道的流量；Tout和Tin分别为节点混合温度和水流流入温度。

1.3 天然气系统数学模型

天然气稳态能流模型常采用Weymouth 方程［20］进行表征,表达式为：

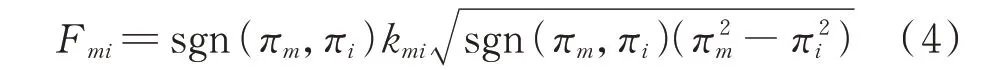
式中：Fmi和πm分别为管道m-i的流量和节点m的气压；kmi为管道特性参数；sgn(πm,πi)为符号函数,若πm＞πi则该值为1,否则为-1。

1.4 耦合设备数学模型

电网、热网、气网中能源形式各不相同,需要利用耦合设备实现不同能量流的转化。本文考虑的耦合设备包括电转气、燃气发电机、热电联产机组。

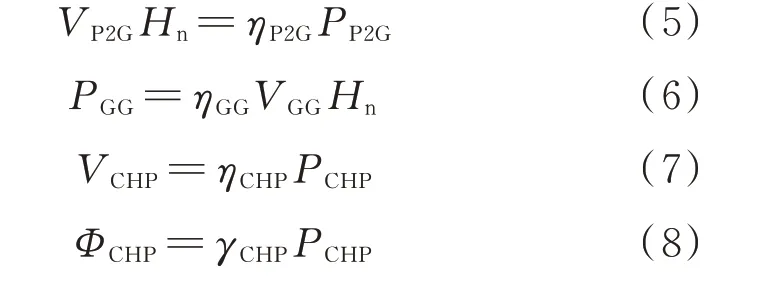
式中：Hn为天然气热值；VP2G和PP2G分别为电转气发出的天然气流量和消耗的电功率；VCHP、PCHP和ΦCHP分别为燃气热电联产设备消耗的天然气流量和其发出的电、热功率；VGG和PGG分别为燃气发电机消耗的天然气流量和发出的电功率；ηP2G、ηGG、ηCHP和γCHP为与转换效率有关的比例系数。

1.5 基于牛顿拉夫逊法的多能流计算数学模型

将电力系统中牛顿拉夫逊法潮流计算模型运用至多能流计算中,求解式（1）—式（8）构成的IES 多能流计算数学模型,该模型中的待求状态变量包括电网的节点电压相角矩阵θ与幅值矩阵V、热网的管道流量矩阵m与节点供回水温度矩阵T、气网的节点气压矩阵π。若存在压缩机管道,则采用文献［21］中方法进行处理,将其转化为节点等效负荷。最终,由修正量及雅克比矩阵J构成的迭代方程为：

式中：ΔW为输入变量的不平衡量矩阵；ΔX为状态变量的不平衡量矩阵；ΔP和ΔQ分别为节点有功功率及无功不平衡量矩阵；ΔF为气网节点流量不平衡量矩阵；ΔT为包含供水管道节点温度不平衡量和回水管道节点温度不平衡量的矩阵；ΔΦ为节点热功率不平衡量矩阵；Δθ为节点电压相角不平衡量矩阵；ΔV为节点电压幅值不平衡量矩阵；Δm为热网管道流量的不平衡量矩阵；Δπ为节点气压平方的不平衡量矩阵。

2 IES 运行风险量化评估

IES 中存在着诸多不确定性因素,如分布式新能源出力和负荷的随机波动。为了分析不确定性因素带来的影响,基于如下的概率多能流计算建立运行风险指标。

2.1 IES 概率能流计算

为了保证风险评估的快速性,采用基于半不变量法的概率能流计算。该方法与常规的电力系统概率潮流计算有相似之处,本质都是利用已知随机变量的矩与半不变量求出待求量的概率分布。

本文计及的随机变量包括随机性新能源出力和电、热、气负荷,其v阶原点矩为：

最后,结合Gram-Charlier 展开级数［22］快速求解出θ、V、m、T、π的概率密度和概率分布。

2.2 IES 运行风险指标定义

基于概率能流计算得到的状态量概率分布,定义风险指标,包括电网节点电压越限风险及线路过载风险、热网节点温度越限风险及管道流量越限风险、气网节点气压越限风险及管道流量越限风险。

采用指数型效用函数刻画电压越限严重程度,在此基础上,基于概率能流算法,综合考虑越限概率与越限严重程度,定义节点电压越限风险指标为：

热网的流量越限风险和节点温度越限风险以及气网的流量越限风险和气压越限风险定义与电网风险定义类似,其表达式见附录A 第A1 章。

3 IES 运行韧性量化评估

前文运行风险评估是用于分析正常运行过程中风、光、荷等随机因素波动下IES 安全性水平的一种方法,着重考虑高概率低严重度的小扰动事件对系统的影响。针对低概率高严重度的事件,如地震等小概率极端灾害造成的线路或管道故障,单从概率角度分析无法得知其对IES 造成的恶劣影响,本文从运行韧性的角度加以分析。通常认为,电力系统韧性包含充裕性、鲁棒性和快速性等方面［23］,充裕性越好,极端灾害下故障发生的可能性越小；鲁棒性越好,故障发生时系统的失负荷量越小；快速性越好,故障后负荷恢复越迅速。本文将电力系统韧性的定义进行扩展,建立极端事件下的IES 运行韧性指标。需要说明的是,韧性是一个内涵较为丰富的概念,本文重点在于评估层面,关注故障发生后的鲁棒性,鲁棒性评估结果可以辅助IES 进行灾后恢复。

3.1 IES 运行韧性指标定义

本文选择地震作为极端自然灾害,该场景下电、热、气网的线路及管道故障概率模型参考文献［18］。对于极端自然灾害出现时每种故障状态下的IES,本文从失负荷量的角度提出IES 运行韧性指标为：

3.2 IES 运行韧性指标计算

采用最优切负荷模型计算韧性指标。首先利用拉丁超立方抽样［24］对分布式新能源出力和负荷功率进行随机采样获取场景集。为减少计算负担,采用同步回代削减技术［25］获取典型场景。以极端情况发生时的负荷削减量最小为目标函数：

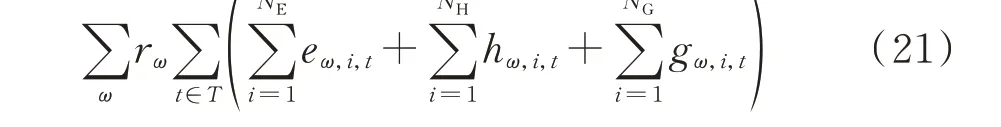
式中：rω为场景ω出现的概率；eω,i,t、hω,i,t和gω,i,t分别为电、热、气网在ω场景t时刻节点i的失负荷量；T为时刻集合；NE、NH和NG分别为电、热、气网的节点数。

3.2.1 电网约束

对于每个典型场景,电力系统需要考虑如下的约束条件。

1）电负荷削减量约束

式中：am,t为t时刻节点m气压的平方；kmi,t为t时刻管道m-i的特性参数；Fmi,t为t时刻管道m-i的流量。

进一步,对上式进行增量分段线性化处理,得到线性化的网络约束：

4 IES 薄弱环节辨识

系数,其求取方法见附录A 第A3 章。

上述薄弱节点辨识方法用于辨识系统的短板,对于极端事件,由于多能流系统中多种可调度资源的存在,一方面可以通过优化控制尽可能降低灾害发生时的负荷损失水平；另一方面通常会有相应的预案实现灾后负荷恢复。因此,在权重系数确定方面不需要对韧性指标做出很高的冗余,以防评估结果过于极端。

管道或支路的风险-韧性双维度综合指标用于寻找薄弱管道或支路,电、热、气网中故障线路和故障管道的薄弱环节辨识综合指标分别为LEk、LHk、LGk,其表达式分别为：

根据上述指标寻找IES 薄弱环节,综合评估流程如附录B 图B1 所示。

5 算例分析

本文算例基于改进的IEEE 33 节点配电网、比利时20 节点气网和13 节点热网构成的IES。在配电网中,节点11 和31 接入风电机组,基准容量为1.5 MW 和2 MW。风电及负荷具有随机性,风速在一段时间内服从Weibull 分布［28］,尺度参数和形状参数分别为7.2 m/s 和2,风机出力模型参考文献［28］,其切入、切出及额定风速分别为3 m/s、25 m/s 和15 m/s,各节点负荷服从正态分布。系统架构和源荷数据见附录B 图B2 和图B3,预测值为风电出力及负荷的期望值。

5.1 半不变量法概率能流有效性验证

基于23：00 时的时序运行数据,采用本文方法计算状态量的概率密度。并将蒙特卡洛法模拟10 000 次的结果作为标准值判断本文方法的准确性,结果如附录B 图B4 所示。图B4 为热网管道13-1 的流量、气网节点15 气压的平方、电网节点22电压幅值和支路32 有功功率的概率密度图。2 种方法所得结果较为接近。因此,本文方法具有一定的准确性。模拟法和本文方法的用时分别为232.67 s和7.05 s,可见本文方法在保证一定精确性的同时可以减小计算耗时,适用于实时的运行风险评估。

5.2 风险指标分析

分析负荷波动这一随机因素对风险指标的影响,分别在以下2 种情况下计算系统的风险值。场景1：电、热、气负荷波动标准差分别为0.20、0.10、0.15。场景2：电、热、气负荷波动均有一定程度的增加,分别为0.50、0.20、0.20。IES 的风险分布见图1。

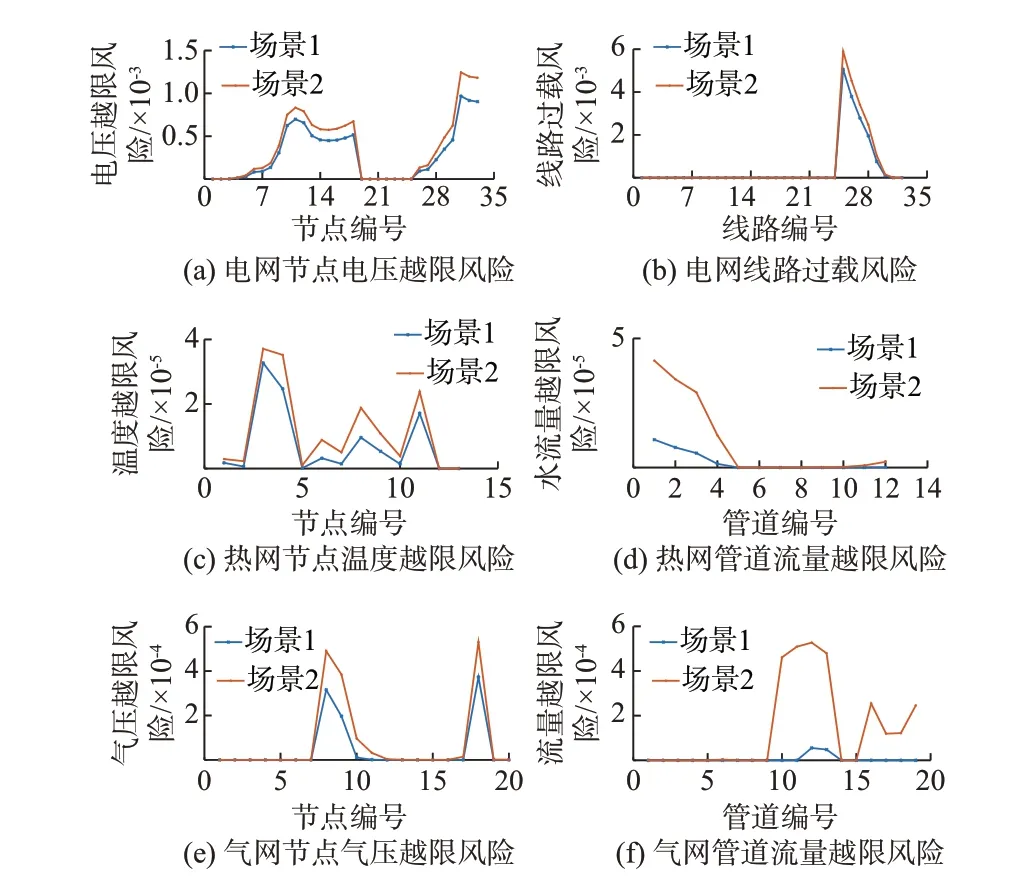
图1 不同负荷波动标准差下的风险值Fig.1 Risk value under different standard deviation of load fluctuation

此外,电热气耦合关系的存在也会使一个子系统的变化影响到与之耦合的其他系统。当热网负荷波动标准差分别为0.1 和0.2,电网、气网负荷波动标准差保持场景1 中的值不变时,电网和气网的风险值如附录B 表B1 所示。结果表明,当热负荷波动增加时,电网及气网的风险值将会变大。这是因为热负荷波动会造成耦合设备出力变化,进而对其他子系统的风险造成影响,但风险值会小于电、热、气负荷波动量同时增加的情况。

计算场景1 中每个时刻IES 的综合风险,结果如图2 所示,综合风险定义见附录C。

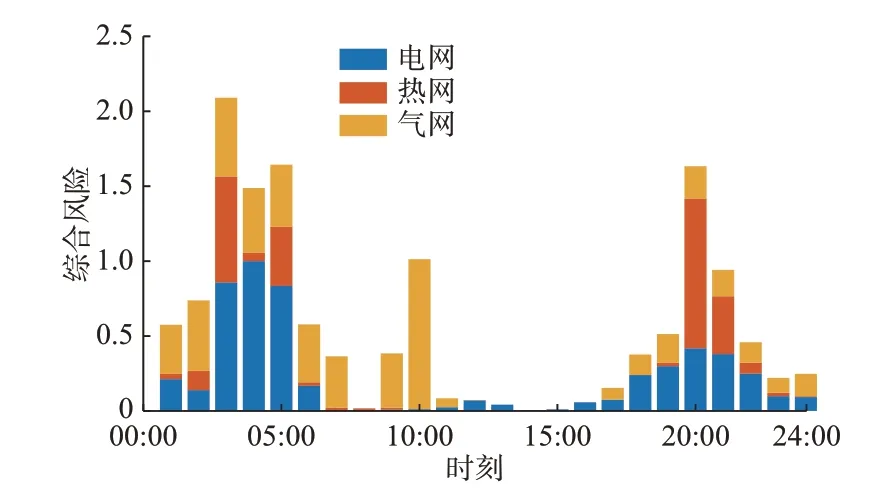
图2 IES 各时刻的综合风险Fig.2 Comprehensive risk of IES at each moment

由图2 可知,电、热、气网综合风险最大的时刻分别在04：00、20：00 和10：00。04：00 时风电出力最大,会带来较大的节点电压越限风险；20：00 时热负荷量最大；10：00 时气负荷量最大,会带来较大的管道流量越限风险。

5.3 计及极端情况的韧性指标分析

本文考虑的极端自然灾害为地震,地震发生时的故障场景集见附录D 表D1,以故障2 为例计算韧性指标。为实现时序分析,本文以1 h 为时间间隔计算IES 在1 d 的韧性指标,如图3 所示。

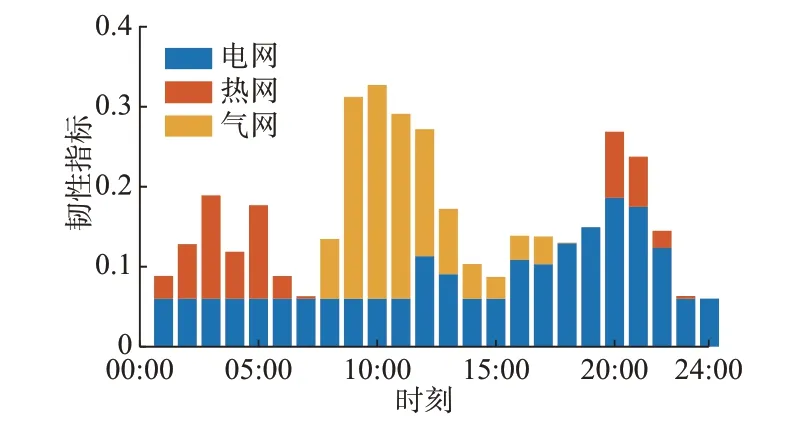
图3 IES 各时刻的韧性指标Fig.3 Resilience index of IES at each moment

由韧性指标的时间分布图可知,09：00—12：00和20：00 时的综合韧性指标较大,鲁棒性差。09：00—12：00 时,风电出力较小,电负荷处于次高峰状态,气负荷量也较重。若该时段出现电网支路30-31 断线,一方面处于孤岛部分的节点全部停电；另一方面由于故障发生,孤岛部分与主网失去联系,节点31 的电转气设备仅能依靠风机发出的电能实现电到气的转化,产气量低且具有随机性,使得气网的重载情况进一步加重,需要切除较大的负荷量维持IES 的安全稳定运行。

5.4 基于风险与韧性的薄弱环节辨识

综合考虑极端自然灾害发生时的韧性指标和正常运行情况下场景1 的风险指标,得到薄弱节点辨识结果,如图4 所示。

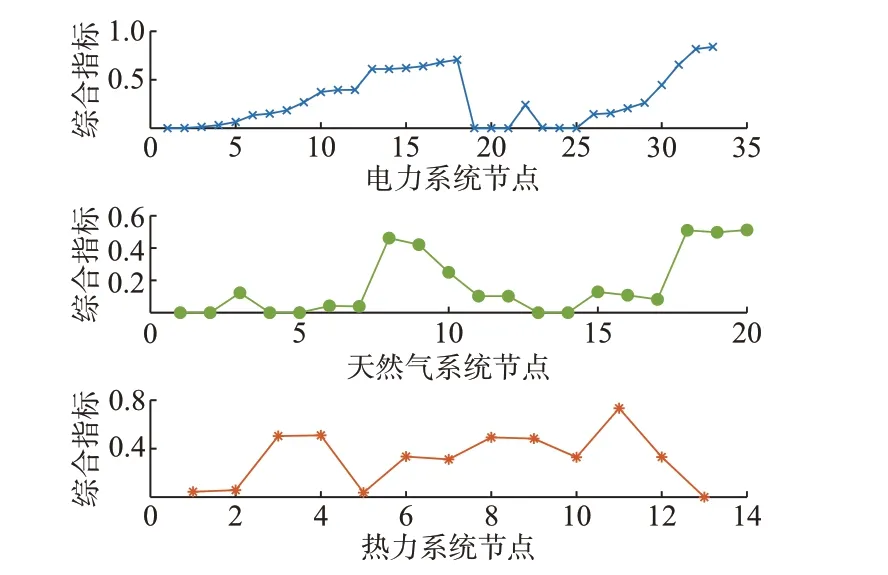
图4 IES 各节点的综合指标Fig.4 Comprehensive index of each bus in IES

电网最脆弱的节点为节点33,一方面,该节点在系统无故障运行状态下有较大的电压越限风险；另一方面,当故障包含线路29-30、30-31、31-32、32-33 时,均会出现节点33 的负荷被削减的情况。气网最脆弱的节点为节点20,节点8 虽不在故障集所包含的区域内,但综合指标也较大,这是因为节点8 在无故障运行时存在较大的节点气压越限风险。热网最脆弱的节点为节点11,该节点既处于故障集包含的区域,在无故障运行时也存在较大的温度越限风险。

各故障支路的薄弱环节辨识综合指标见附录D图D1,电网中最脆弱的支路为12-13,热网中最脆弱的支路为4-12,气网中最脆弱的支路为18-19。在运行过程中应当着重关注这些线路,采取措施降低其正常运行时的越限风险,并实施加固措施,降低其在极端灾害发生时发生故障的可能性。

图5 为IES 每个时刻的风险-韧性双维度综合指标,电网最脆弱的时刻为04：00,气网和热网最脆弱的时刻分别为10：00 和03：00。对于整个IES 而言,03：00 时系统的综合指标值最大,IES 的总体薄弱性最强,此时热负荷量较重,风电出力到达了峰值而负荷量为谷值,因此存在一定的节点电压越限风险和线路过载风险,且若极端灾害造成热网管道故障,会带来较大的热力系统失负荷量。10：00—11：00 和20：00 时的综合指标也较大。10：00—11：00 时,气负荷、热负荷均较重,风电出力较小,若极端状况在该时段发生,特别是当故障包含了电转气和风机所在支路时,会导致供能水平有所降低,系统整体的失负荷比例较大,风险-韧性双维度综合指标较大。20：00 时,电、热负荷达到峰值,IES 处于重载状态。一方面,存在较大的线路过载风险；另一方面,极端灾害条件下的故障也会造成较大的失负荷量,因此综合指标也较大。在运行过程中应当着重关注这些辨识指标较大的薄弱时刻,提前采取经济调度等相关预防措施,维持IES 安全稳定运行。

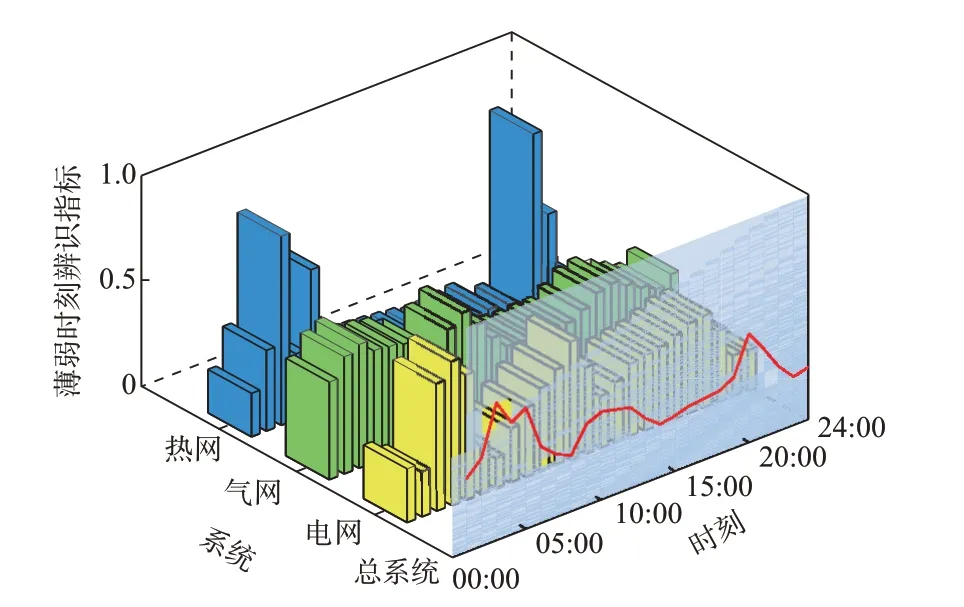
图5 IES 运行薄弱时刻综合指标Fig.5 Comprehensive index of IES risky operation moment

为进一步分析风险与韧性相结合的评估方法的优越性,本文将仅考虑风险、仅考虑韧性、同时考虑风险与韧性的薄弱环节辨识结果进行对比,如附录D 图D2 所示。仅考虑风险时,式（36）—式（41）等号右边的第2 项和式（42）—式（44）等号右边的第3 项为0,仅考虑韧性时,式（36）—式（41）等号右边的第1 项和式（42）—式（44）等号右边的第1 和第2项为0。由附录D 图D2（a）可知,仅考虑风险时,电网节点22 的综合指标为0,但节点22 处于故障集所包含的区域,因此,仅考虑风险不能合理评判节点22 的薄弱性。由附录D 图D2（b）可知,仅考虑风险时电网中线路29-30 薄弱性指标最大,热网管道4-12 的薄弱性指标几乎为0；但仅考虑韧性时线路29-30 薄弱性指标最小,热网管道4-12也存在一定的薄弱性指标。因此,单从风险或韧性角度分析薄弱线路或管道都较为片面。由附录D 图D2（c）可知,在11：00—12：00 时,仅考虑风险时薄弱时刻辨识综合指标几乎为0,说明这段时间运行风险较小,但这段时间电、气负荷均较重。因此,该时段的线路或管道故障会带来较大的失负荷量,IES运行具有一定的脆弱性。综合以上分析,将风险与韧性结合的评估方法可以较为全面地评判系统的薄弱性。