基于特征选择实现多因素电力负荷预测
2022-03-23徐先峰王世鑫
胡 欣,冯 杰,徐先峰,王世鑫
(长安大学电子与控制工程学院,陕西 西安 710064)
0 引言
随着我国电力市场化改革的深入发展以及新能源的逐渐应用,不仅电力行业对负荷预测的精度要求越来越高,而且在负荷数据不断丰富的情况下,剔除冗余因素以提取出关键因素也给负荷预测带来了一定的挑战[1]。因此,在选择科学、合理的负荷预测方法的同时,全面分析研究各因素之间的联系,对于提高负荷预测精度至关重要。
历史负荷数据通常蕴含着自身特性及其相关变化规律。深入挖掘剖析历史信息,并将其延伸至预测未来趋势,是电力负荷预测领域的常用数据基础之一。文献[2]利用聚类算法和门控循环单元网络,提高预测性能。文献[3]提出基于K近邻的深度学习方法。文献[4]提出了一种基于长短期记忆(long short-term memory,LSTM)网络和极速梯度提升方法的组合预测模型,均改善了预测准确性。文献[5]结合了评价指标和优化算法,实现了负荷预测。文献[6]提出了由单一乘性神经元模型、粒子群优化算法和非线性滤波器组成的混合方法。上述基于历史负荷数据预测只是考虑到历史负荷的变化规律对未来用电量的影响,没有涉及其他外在因素的作用。但是随着电力行业的不断发展,越来越多的学者也考虑到其他外在因素对负荷预测产生的影响。文献[7]和文献[8]同时考虑了历史负荷数据和气象因素,利用LSTM实现负荷预测。文献[9]结合了电价,提出了基于卷积神经网络和LSTM相结合的预测模型。文献[10]在历史负荷数据基础上,考虑了气象和季节因素两方面,提出基于电力负荷因子的深度聚类神经网络。文献[11]针对温度、日期以及历史数据,提出了注意力机制的多层门控循环单元网络进行多步预测。
从上述文献可以看出,大多数研究只是针对历史负荷数据或者人为主观指定外在因素来实现负荷预测。但是在日新月异的电力行业中,采集的负荷数据越来越丰富,使得对电力负荷预测产生影响的因素不仅局限于历史数据或者气象因素等,还包括其他一些外在因素,比如电价、温度等;各因素对负荷变化的作用或大或小,如果仅凭主观指定某一因素作为辅助输入数据,则无法充分挖掘出外在因素对真实负荷的潜在信息。因此,本文在考虑涉及电价、气象等诸多因素的基础上,基于特征选择能寻找最优子集的优势,遴选出与真实负荷相关性较高的关键因素,并且利用注意力机制根据不同影响因素的不同信息,以减少不相关信息干扰的功能,给予重要因素更高的权重,从而搭建基于注意力机制的长短期记忆网络预测模型。
1 基于特征选择的LSTM-Attention预测模型
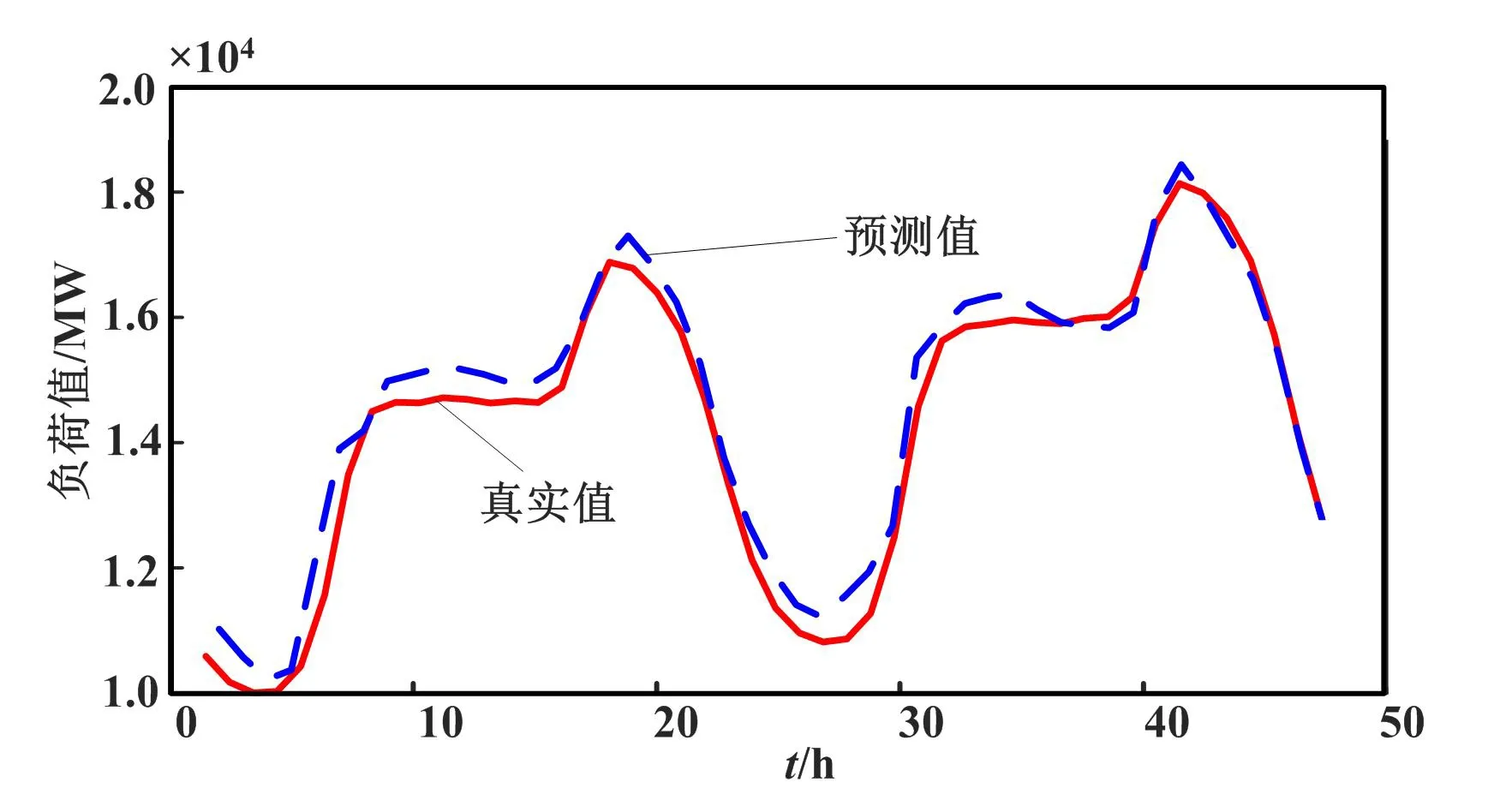
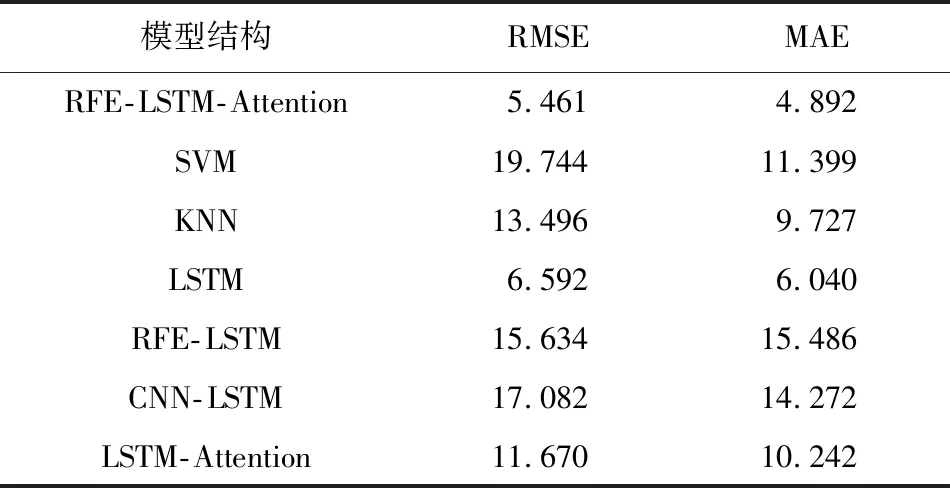
负荷预测领域中的特征选择本质上就是从原始的n个负荷测试样本数据选择m(m 本文结合RFE、注意力机制(Attention)和LSTM的特点,利用RFE自动计算得出的待测历史负荷数据与其他负荷影响因素之间的重要性关系,构造新的输入负荷数据集;将其在不断循环调整输入因素个数的试验过程中,依次引入LSTM中得到输出值,并通过Attention分配权重实现最终的预测结果,从而完成预测性能指标评价。 基于特征选择的LSTM-Attention预测流程如图1所示。 图1 基于特征选择的LSTM-Attention预测流程图Fig.1 Flowchart of LSTM-Attention prediction based on feature selection RFE主要用于评价特征变量的重要性。首先,针对初始负荷特征数据集,通过循环迭代的方式,根据系数选出与真实负荷相关性高的特征(即影响因素)。然后,在剩余的特征上重复这个过程,以此逐渐消除相关性不强的特征,直至达到所需的特征数量。在迭代过程中,特征被删除的顺序就是特征的最后排序。这样能够有效去除冗余的特征变量。RFE具体执行步骤如下。 ①初始的负荷特征集为所有可以使用的特征,需对其进行标准化处理。 (1) 式中:Y*为标准化处理后的负荷数据;Y为负荷数据序列;Ymax为序列Y中的最大值;Ymin为序列Y中的最小值。 ②使用当前特征集进行建模,计算每个负荷特征的重要性,通过循环迭代的方式,根据系数选出与真实负荷相关性高的特征(影响因素);然后,在剩余的特征上重复这个过程,以此逐渐消除相关性不强的特征,直到最终得到所需的特征数量。 ③删除最不重要的一个(或多个)特征,更新特征集。 ④跳转到步骤②,直到完成所有特征的重要性评级。 在电力负荷预测模型学习训练过程中,当外在影响因素输入越多,模型预测性能会更好,也能够保存更多的有用负荷信息。但是这样容易复杂化网络拓扑结构,引起模型学习速度缓慢的问题。因此,为了让相关性小的因素减少对真实负荷的影响度,本文利用注意力机制对输入的13种外在影响因素数据Xi(i=1,2,...,13)进行动态加权的处理方式,以降低与真实负荷相关性较低的影响因素的权重,着重关注相关性高的因素。 以此为基础,本文搭建了基于LSTM-Attention的预测模型,得到最终预测结果Y,以实现高精度的电力负荷预测。 LSTM-Attention模型结构如图2所示。 图2 LSTM-Attention模型结构图Fig.2 LSTM-Attention model structure diagram 如今,注意力机制已成为深度学习神经网络的重要组成部分,并且在自然语言处理、统计学习、语音翻译和计算机视觉等领域具有大量的应用。注意力机制源自人类的视觉直觉。人类视觉快速扫描图像全局选择性地关注一部分目标区域,即所谓的关注焦点,在抑制其他无用信息的同时,更多地关注目标的重要信息。注意力机制[11]可以根据输入数据的不同特征动态调整重视程度的一种学习机制:对于输出结果的重要信息,给予更高的权重;同时,减少不相关信息的干扰。因此,该模型可以更好地学习有效信息。在引入注意力机制的LSTM模型的实现过程中,将参与负荷预测试验的一系列历史数据X看作是由寻址操作中的存储内容数据的地址Key和该数据对应的注意力值Value组成的,则通过计算给定元素和各个Key的相似性或者相关性,可得到每个Key对应Value的权重系数,再对Value进行加权求和,即可得到最终的注意力数值。注意力qi的计算式如式(2)所示。 (2) 式中:vi为注意力机制中第i个数据的注意力值;ai为vi的权值系数。 ai的具体计算方法如式(3)所示。 (3) 式中:Si为第i个数据的余弦相似性。 (4) 式中:Ki为输入负荷信息第i个数据对应的地址。 LSTM改善了循环神经网络可能会引起梯度消失或爆炸的问题,能够存储较长时间的信息,并且可以使模型获得更好的预测效果[13]。 LSTM模型结构如图3所示。 图3 LSTM模型结构图Fig.3 LSTM model structure diagram ①遗忘门。根据当前的输入负荷信息xt和(t-1)时刻负荷信息的输出ht-1,共同确定LSTM需要剔除(t-1)时刻负荷状态信息冗余的部分。 ft=σ{Wf·[ht-1,xt]+bf} (5) 式中:ft为遗忘门;σ为Sigmod函数;Wf为遗忘门的连接权重矩阵;bf为遗忘门的偏置项;·为矩阵相乘。 it=σ{Wi·[ht-1,xt]+bi} (6) (7) (8) ③输出门。决定将被用作当前状态的输出状态ht。ht-1和xt先通过Sigmod激活函数得到ot,以控制负荷预测输出;接着利用tanh函数将Ct值变换至[-1,1]之间;最后将变化结果与ot相乘,得到新的负荷预测状态ht。 ot=σ{Wo·[ht-1,xt]+bo} (9) ht=ot·tanh(Ct) (10) 式中:ot为输出门;Wo为输出门的连接权重矩阵;bo为输出门的偏置项。 为验证本文算法的有效性,利用新英格兰地区电力负荷数据集进行试验分析。数据集包括2014年共365天的负荷数据。同时,考虑了日前竞标负荷、真实负荷、电价温度、湿度等13个负荷影响因素,并每隔一小时采集一次数据,共得到8 760个数据样本。本文选取真实负荷为待测负荷因素,其余因素为辅助影响因素。在试验时,选择2014年9月1日到11月30日共2 184条数据作为训练集、12月1日和12月2日两天共48条数据作为测试集。 新英格兰地区数据集说明如表1所示。 表1 新英格兰地区数据集说明Tab.1 New England regional data set description 表1中采集时所涉及的因素首先考虑到了新英格兰所处的地理位置情况。由于该地区靠近大西洋,容易受近海的寒流影响,导致其每年降水量和降雪量较大,尤其第四季度的寒冷天气,加剧了人们的供热需求,故温度和湿度的数据采集必不可少。其次,新英格兰的电力市场管制比较放松,市场参与成员可以通过竞拍购买或者发售一定的输电权,也可以在二手市场中进行自由交易[14]。这期间,一旦竞争激烈,电价随时可能因各种原因产生波动。而且电力市场会因用户的需求高峰期而带来价格的剧烈上涨,对该地区的用电量也会产生不小的影响。由此可见,在对该地区进行负荷预测的过程中不能忽视电价对负荷的影响。为了更全面地考虑上述因素对历史负荷数据的影响,本文采用RFE对各负荷影响因素数据进行重要性排序,结合LSTM的长时记忆功能,以及注意力机制的权重分配优势,实现多因素电力负荷预测,为预测电力需求变化趋势提供理论依据。 RFE评价得出了13个影响因素对真实负荷的重要性排序。部分RFE排序结果的对应因素如表2所示。排序中的K值表示每次试验包含关键性因素的个数。 表2 部分RFE排序结果的对应因素Tab.2 Corresponding factors of partial RFE ranking results 根据试验最终选择的关键因素,分析原因除了文中2.1节提到的采集电价因素原因之外,还与竞标负荷及电力行业各部门的利益密切相关。如果真实负荷最终小于竞标负荷,被市场统筹调度的可能性会很小,造成电能资源浪费;反之则会影响电网稳定,不利于电力市场的运行调度。而且,竞标负荷往往是根据历史负荷数据的变化规律确定的。另外,阻塞电价通常会对电力负荷造成影响。当阻塞区内出现电量相对稀缺时,由于电力市场一般不是竞争市场,发电公司为获得高额利润,使用保留部分可调度发电容量或采用报高价等策略,以实现其市场势力。同时,温度、湿度也会造成一定的影响,主要体现在特定时间段内对电器的过渡使用造成负荷的波动。因此,试验结果所选择的关键因素较符合实际情况。 为了评价文章提到的模型预测效果,本文选择了均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)这2个性能指标作为负荷预测的评价指标。这2个指标的计算如式(11)和式(12)所示。 (11) (12) 本次试验中,LSTM模型采用自适应矩估计(adaptive moment estimation,Adam)优化算法,根据前一小时历史负荷数据,结合特征选择算法遴选的其他负荷影响因素,预测下一小时通过计算梯度的一阶矩估计和二阶矩估计,为不同的参数设计独立的自适应学习率。经过多次超参数试验,最终确定的部分超参设置如下:隐藏层神经元数量为50个;步长为100;批大小为72个;学习率为0.01。 经过试验仿真,RFE-LSTM-Attention预测曲线如图4所示。 图4 RFE-LSTM-Attention预测曲线图Fig.4 RFE-LSTM-Attention prediction curves 图4中:实线表示真实值;虚线表示预测值。此时,递归特征选择算法选出的关键因素个数为3,即真实负荷、日前阻塞电价以及日前竞标负荷时,预测效果最佳。从图4中也可以看出,预测值与真实值具有较高的拟合程度。 为了验证使用的方法有效性,本试验计算了模型的RMSE和MAE,选取了仅使用历史负荷数据时的K-近邻(K-nearest neighbor,KNN)、LSTM、支持向量机(support vector machine,SVM)、LSTM结合卷积神经网络(convolutional neural network,CNN)、LSTM-Attention以及RFE-LSTM作为对照试验。对比算法试验结果如表3所示。从表3中可以看出,RFE-LSTM-Attention的RMSE和MAE更小。与SVM相比,RFE-LSTM-Attention的RMSE和MAE分别降低了14.283和6.507。而且与适合处理长序列数据的LSTM相比,RFE-LSTM-Attention预测性能相对更优。 表3 对比算法试验结果Tab.3 Experimental result of comparison algorithm 为了进一步提高电力负荷预测精度,本文提出了RFE-LSTM-Attention的电力负荷预测模型。在新英格兰地区的原始数据集的基础上,以遴选关键因素为切入点,利用RFE按照重要性自动排序关键因素,从而生成新的数据集。基于Attention分配权重的优势,搭建了LSTM-Attention电力负荷预测模型,并进行了仿真试验。从预测结果可以看出,RFE-LSTM-Attention提高了整体预测精度。与其他单一算法、组合算法对比,RFE-LSTM-Attention的误差最小,具有良好的预测性能。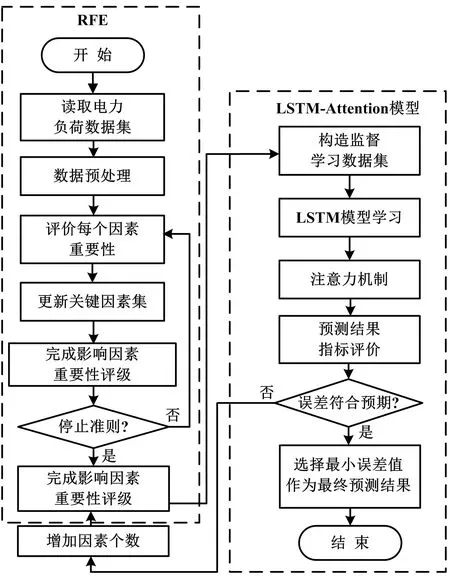
1.1 基于RFE的关键因素遴选模块
1.2 LSTM-Attention电力负荷预测模型

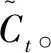
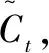
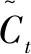
2 LSTM-Attention预测模型分析
2.1 数据集分析

2.2 关键因素分析

2.3 评价指标
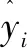
2.4 超参数设置
3 试验结果分析
3.1 试验结果
3.2 对比试验
4 结论
