采样率对PMSM的SMC控制性能影响研究
2022-03-23马家庆
颜 坤,马家庆
(贵州大学电气工程学院,贵州 贵阳 550025)
0 引言
近年来,随着经济的飞速发展,国内自动化水平迅速提升,以电机为核心的驱动控制领域取得了长足进步,并且深入到各行各业。为了使永磁同步电机(permanent magnet synchronous machine,PMSM)性能指标更加突出,不仅需要对控制器进行研究,还需要匹配对应性能指标最优的采样率,以实现更高的效率。Utkin和Emelyanov[1-2]提出的滑模控制(sliding mode control,SMC)是一类可变结构系统。目前,SMC已在许多领域成功实施,在滑动面设计方面,有学者选择比例积分(proportional integral,PI)滑模面[3],也有学者选择比例微分(proportional differential,PD)滑模面[4]。已有学者证明,比例积分微分(proportional integral differential,PID)滑模面可提供比PD滑模面更快的响应[5]。
本文提出了一种新型分数阶双幂次快速趋近率,通过理论与仿真证明所提新型趋近率的稳定性、可达性以及存在性。
在计算机控制系统中,为了使计算机能处理被控对象的输入和输出信号,首先要将误差信号这一模拟量按一定的采样周期T进行采样。采样率控制系统的研究也开始得较早。通过单采样率设计,保证了离散时间模型输入状态的稳定性[6]。此外,也有学者提出频域分解方法,以及传递函数的方法[7]。本文通过采样率对最小相位系统理论分析,试验验证理论的可行性,并得出采样率对永磁同步电机的滑模控制性能影响的结论。
1 采样率对控制系统理论分析
采样定理是将连续时间信号转变为离散时间信号的有效工具[8]。当永磁同步电机没有负载时,其矢量控制模型可通过标准形式表达为:
(1)
式中:x(t)为系统状态变量,x(t)∈Rn;u(t)为系统控制输入,u(t)∈Rn;y(t)为系统输出观测量y(t)∈Ra;A∈Rn×n、B∈Rn×m、C∈Ra×n、G1∈Rn×b均为系统矩阵。
由于电机矢量控制系统中存在包含滑模非线性控制器在内的非线性部分,所以f[x(t)]∈Rb总存在一个非负常数μ,使之满足Lipschitz条件:

(2)
假设:系统矩阵(A,C)可观和(A,G1)可控,且(A+αI,G1,C)满足最小相位最小相位条件;I为单位矩阵;参数α>0。
对于无负载的矢量控制系统,设计采样观测器如式(3)所示。
(3)
式中:L=QCT∈Rn×a,Q为对称对称正定矩阵,并且可通过LQ Riccati方程求得。
在(A,C)可观和(A,G1)可控的条件下,对于符合α>0和ε>0,始终存在一个对称正定矩阵Q满足LQ Riccati方程[8-9]。而存在对称正定矩阵Q-1,满足LQ Riccati方程的条件是当且仅当式(4)成立。
(4)
定义参数ε>0和δ>1。若满秩矩阵C和G1满足rank(CT)=rank(G1),且(A+αI,G1,C)是最小相位系统,那么存在正定矩阵Q-1满足以下条件:
(5)
(6)
通过式(5)和式(6),求出正定矩阵Q和参数ε。若存在采样周期T满足不等式(7)条件,则说明对任意常数μ的误差估计系统是全局指数稳定。对于不等式(7),一定存在一个足够小的采样周期T。则T为式(7)的最优解[9]。
(7)
2 滑模控制器设计及仿真分析
2.1 滑模控制器设计
本文提出一种新型分数阶双幂次快速趋近率,为:
(8)
式中:k1>0;k2>0;0 系统能快速趋近滑模面。当系统接近滑模面时,趋近速度能较快降低并稳定在滑模面附近,而幂函数能明显解决系统抖振问题。 通过李雅普洛夫(Lyapunov)函数,证明提出的新型趋近率的可达性和存在性: (9) 对式(9)求导,并将式(8)代入式(9),有: (10) 用滑模控制器代替传统矢量控制中速度环的PI控制器。定义以下非线性滑模面切换函数: s=cx1+x2c>0 (11) 式中:c为待定参数;x1为系统状态变量。 定义PMSM状态变量: (12) 式中:ωref为电机参考转速,通常为常量;ωma为电机实际转速。 对式(11)求导,并将式(12)代入式(11)。令s=σ,有: (13) (14) 图1 滑模控制器仿真模型Fig.1 Simulation model of sliding mode controller 三种控制器速度响应曲线如图2所示。图2中,分别为基于PI控制器、基于指数趋近率的滑模控制器以及基于新型趋近率的滑模控制器的速度响应曲线。在0.2 s处,同时加入10 N·m的负载转矩。 图2 三种控制器速度响应曲线Fig.2 Speed response curves of three controllers 由图2可知,采用PI控制器、基于指数趋近率的滑模控制器以及基于新型趋近率的滑模控制器下的电机速度响应时间分别为0.018 s、0.014 s、0.007 s,超调量分别为253 r/min、222 r/min、6 r/min。在0.2 s加负载后,本文设计的滑模控制器的鲁棒性能明显高于PI控制器。 三种控制器电机定子三相电流如图3所示。由图3可知,新型趋近率的定子三相电流脉动较小。新型趋近率控制器电机空载启动到稳定时间约为0.02 s,而PI控制器和基于指数趋近率的滑模控制器分别为0.07 s、0.06 s;0.2 s后加入负载。对比结果表明新型趋近率的定子三相电流脉动质量更好。 图3 三种控制器电机定子三相电流Fig.3 Three-phase current of the stator motor of the three controllers 三种控制器电机电磁转矩如图4所示。 由于启动时新型趋近率超调量微小,在0.2 s时加入10 N·m负载后,新型趋近率的抖振相对最小,效果最稳定;PI控制器抖振大,波动明显。 搭建以TMS320F28335为控制核心的PMSM试验平台。平台由计算机、直流稳压电源、驱动板、控制板、PMSM、磁粉制动器搭建组成。 本次试验电机的型号为ACSM80。电机额定电压为220 V,额定功率为0.75 kW,额定转矩为2.4 N·m,最大转矩为7.2 N·m,额定转速为3 000 r/min,额定电流为4.22 A,相电阻为0.901 Ω,相电感为6.552 mH,极对数为4对。 这里对电机的速度响应在不同采样率下进行试验分析,即分别测试永磁同步电机在滑模变控制器下7~12 kHz的速度响应。试验中,通道1是电机速度响应,对应电机实际转速为1 050 r/min,通过磁粉制动控制器给电机加入4 N·m的负载转矩。 通道1垂直间隔单位为200 mV,水平间隔单位为500 ms。电机转速降通过示波器电压线性表示,单位为mV。通过试验可以看出,电机在7~12 kHz采样率加负载时电机的响应时间分别是715 ms、650 ms、640 ms、660 ms和920 ms。因此,电机在9 kHz采样率时电机响应时间较快。电机在7~12 kHz采样率加负载时电机的转速降低分别是56.6 mV、63.3 mV、63.3 mV、80 mV、86.6 mV和96 mV。因此,电机在7 kHz采样率时其稳态误差最低。 试验还测试了当电机转速为1 050 r/min时加速60 r/min的加速响应情况。从试验中可看出,电机在滑模变控制器下7~12 kHz的提速响应时间分别是238 ms、265 ms、325 ms、318 ms、375 ms和248 ms。显然,采样率在7 kHz时响应时间最短。而在采样率分别是9 kHz、10 kHz、11 kHz和12 kHz时,电机提速出现了超调量,采样率越高其超调量越明显。试验验证在电机减速的时候也具有相同的结论。 由于受到软硬件限制,不排除采样频率受到周期中断的影响。但采样率范围设置在7~12 kHz时,针对转速超调量、响应时间等某一项性能指标有最优采样周期。就上述试验而言,永磁同步电机加负载在采样率为9 kHz时,电机响应时间比较短;在系统允许的范围内适当降低采样率,可使电机转速稳定性相对较高;在电机加减调速时,一定范围内的采样率越高,则其响应时间越长,其超调量也越明显。 本文提出一种新型趋近率,设计滑模控制器并将其应用于永磁同步电机矢量控制系统速度环,再由理论与仿真试验证明其有效性及可行性。通过研究采样率对永磁同步电机滑模控制性能影响,证明了存在任意非负常数u,使得误差估计是稳定收敛的。最佳采样周期T可通过求解多阶线性矩阵不等式得到,即误差估计稳定收敛的最佳采用周期存在。试验分析了采样频率在7~12 kHz电机加减速以及加减负载时的速度响应,得出针对某项性能相对最优的结论:永磁同步电机加载在采样率为9 kHz时电机响应时间较短;加减调速时,在一定范围内采样率越高,其响应时间越长,且超调量越明显。本文设计适用于工程应用。
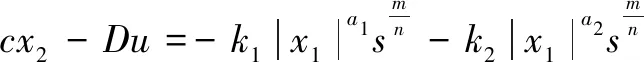

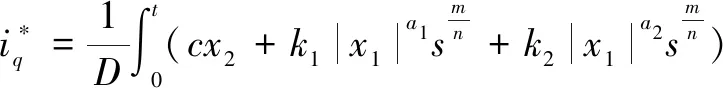
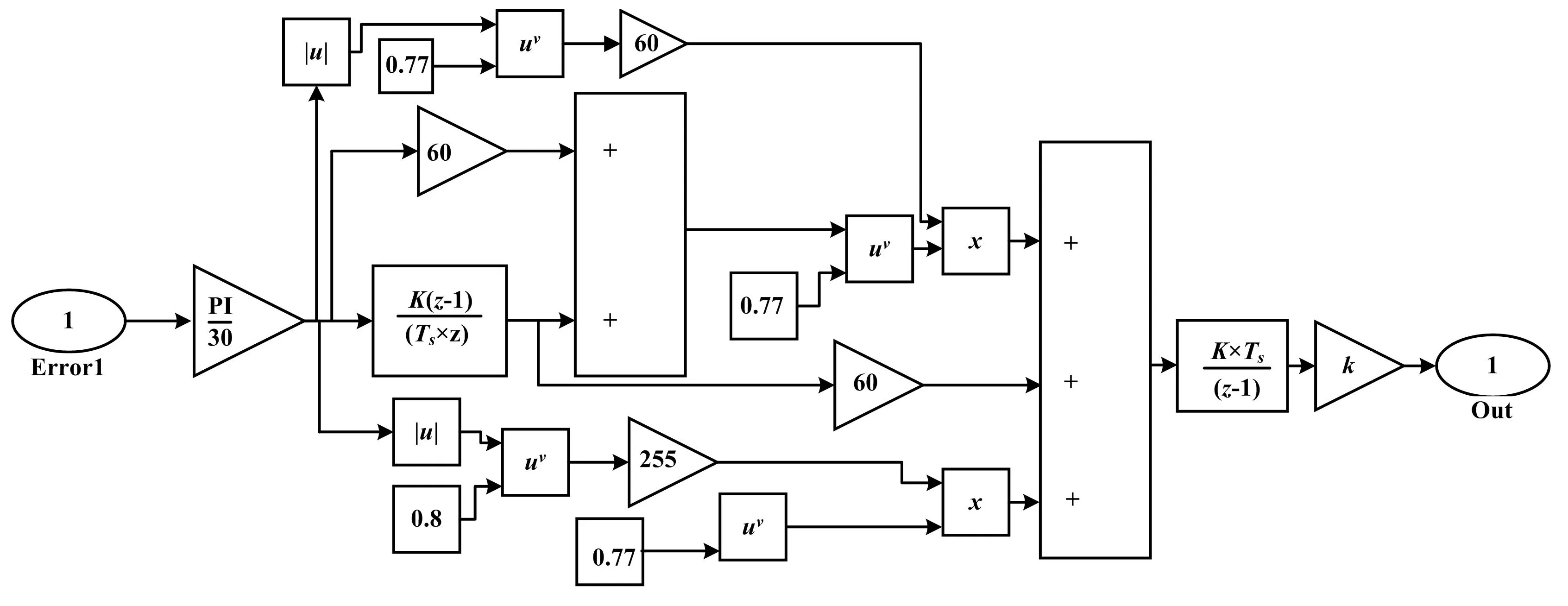
2.2 PMSM滑模变结构控制仿真分析

3 控制系统的平台搭建与试验验证
4 结论
