有源电力滤波器的滤波和无功补偿方法研究

毛以平,董 博,夏 晟,裘 鑫,王善杰

(1.国网浙江宁波市奉化区供电有限公司，浙江 宁波 315000；2.上海电力大学电子与信息工程学院，上海 200000)

0 引言

半导体器件技术[1]的进步推动了电力电子技术的革命。然而，基于电力电子技术的设备，包括调速电机驱动器、电子电源、直流电机驱动器、电池充电器、电子镇流器，也导致了电能质量相关问题的增加。非线性负载产生的谐波电流[2]通过公共耦合点(point of common coupling，PCC)注入配电系统。这些扰动(谐波)是许多问题的根源，会影响与电源相连的电气设备。谐波会导致敏感设备故障、电压应力、导体发热增加以及影响功率因数的网络阻抗谐波电压降。传统的无源滤波器[3]可用于补偿谐波和无功功率。但无源滤波器体积大，存在老化和调谐问题，并且会与电源阻抗发生共振。近年来，有源电力滤波器[4](active power filter，APF)被用于同时补偿电流谐波和无功功率。

并联型有源电力滤波器[5]设计中的一个重要任务是保持与逆变器相连的电容器上的直流电压恒定。这是因为与逆变器可控开关相关的传导和开关功率损耗会导致能量损失，从而降低直流电容器上的电压值。为此，国内外众多学者进行了研究，并取得了丰硕成果。李达义等[6]提出了一种并联型有源电力滤波器的新型控制方法，通过电力电子逆变器产生一个基波电压源施加到变压器二次侧。调节施加到二次侧的电压源的大小，可以使并联变压器对基波呈现为一个可调电抗器，从而实现无功补偿。张国荣等[7]通过瞬时功率流分析得到对直流侧电压波动有影响的功率分量，并在特定的负载条件下对该功率分量进行积分，从而得到电容能量波动精确值。薛花等[8]在建立有源电力滤波器仿射非线性模型的基础上，提出基于李雅普诺夫函数的并联型混合APF非线性控制方法，并设计了电压-电流双闭环控制回路。然而，在大多数时间和大多数工业电力系统中，电源电压可能不平衡及失真。在这种情况下，使用p-q理论的控制不能提供良好的性能。

为有效解决电源电压不平衡及失真问题，本文对一种并联型APF拓扑进行了分析和仿真。该拓扑能够在电网电压不平衡的情况下同时实现谐波电流阻尼和无功补偿。

1 系统构成

三相供电系统APF方案如图1所示。

图1 三相供电系统APF方案Fig.1 APF solution for three-phase power supply system

负载可以是单相、两相或三相，通过定义负载非线性的桥式整流器平衡或不平衡地连接到供电干线。在这种情况下，三相非受控二极管桥式整流器的电阻感性负载被认为是非线性负载连接到电源。这种负载从供电干线吸取非正弦电流。基于绝缘栅双极晶体管(insulate gate bipolar transistor，IGBT)的电压源逆变器用作电能质量补偿器，以补偿非线性负载产生/需要的必要谐波和无功功率。此外，系统采用的逆变器由六个电压应力为Vdc的IGBT开关、一个直流电容和三个升压电感组成。逆变器由基于滞环规则的无载波脉冲宽调度剂(pulse width modulation,PWM)电流控制技术控制。其表现为受控电流源。

2 控制策略及系统架构设计

2.1 控制策略

基于瞬时功率理论的控制策略指出，电压型逆变器(voltage source inverter，VSI)可以瞬时提供无功功率并补偿非线性负载的谐波。这个假设形成了著名的p-q理论。根据p-q理论，由开关器件组成的瞬时无功功率补偿器实际上不需要任何储能元件，可以补偿瞬时状态下的基波无功功率以及由负载瞬时虚功率引起的谐波电流。

根据式(1)和式(2)，基本p-q理论由a-b-c坐标系中测量电源电压(vsa,vsb,vsc)和负载电流(iLa,iLb,iLc)到α-β坐标系的代数变换组成，然后计算瞬时功率分量(p,q)。

(1)

(2)

瞬时实功率p和虚功率q的计算如下所示：

(3)

此外，瞬时实功率和虚功率包括交流值和直流值，可表示为：

(4)

此外，负载电流的α-β分量可分为α-β轴瞬时真实分量和负载电流的无功分量。根据负载瞬时实际功率和无功功率的直流和交流分量，负载电流的两个重要方程式可表示为：

(5)

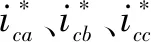
基本p-q理论控制算法如图2所示。

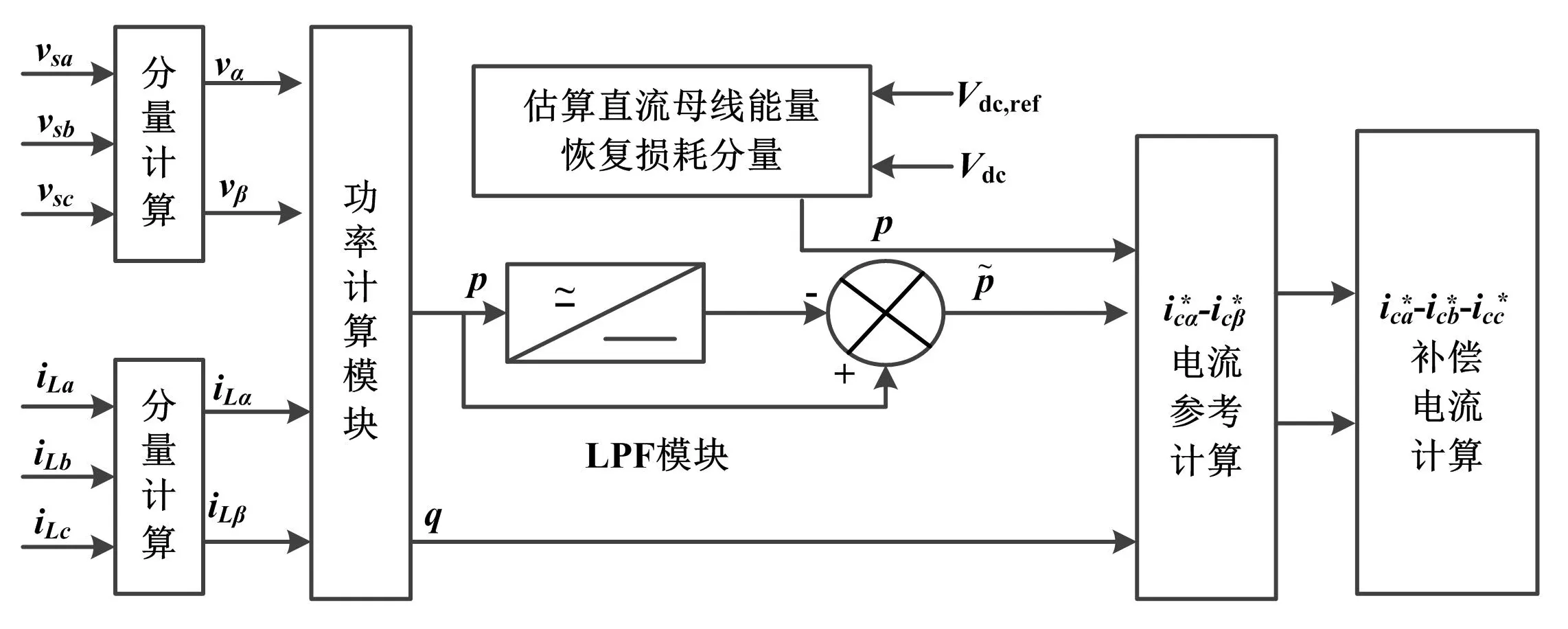
图2 控制算法框图Fig.2 Block diagram of control algorithm

通常情况下，可利用低通滤波器[9]将基波分量与实际情况下不理想的电压分离。但由于其存在相位和增益精确调谐的问题，需要三个以上的电流传感器来检测负载电流。同时，特定阶数和截止频率的确定对滤波器的设计也起着重要的作用。因此，该方法采用神经网络从电源电流中提取基波分量，而不是从非理想电源的负载电流中提取基波分量，只计算由基波分量引起的实际功率。

2.2 控制架构设计

控制结构的重要组成部分是参考信号的估计。p-q理论适用于理想电源电压，但在非理想电源电压条件下不适用[10]。瞬时实功率和虚功率的交替值具有电流谐波和电压谐波。因此，有源电力滤波器产生的补偿电流不等于电流谐波。为了在电源中施加具有适当基频的正弦电流，有必要使用低通滤波器对交流电压进行滤波，从而获得传统p-q理论中使用的基波分量。但是这种低通滤波器在系统中会产生相位延迟，需要对增益和相位裕度进行微调。一个锁相环(phase-locked loop,PLL)块可以用来代替低通滤波器产生基本成分。PLL在电网电压不平衡或失真时性能较差。

为了克服这些局限性，本文提出了基于自适应神经网络逻辑控制的p-q理论，在非理想电源电压条件下，降低一定范围内的总谐波失真。本文采用鲁棒模糊控制器代替低通滤波(low pass filtering，LPF)的方案。控制方案如图3所示。

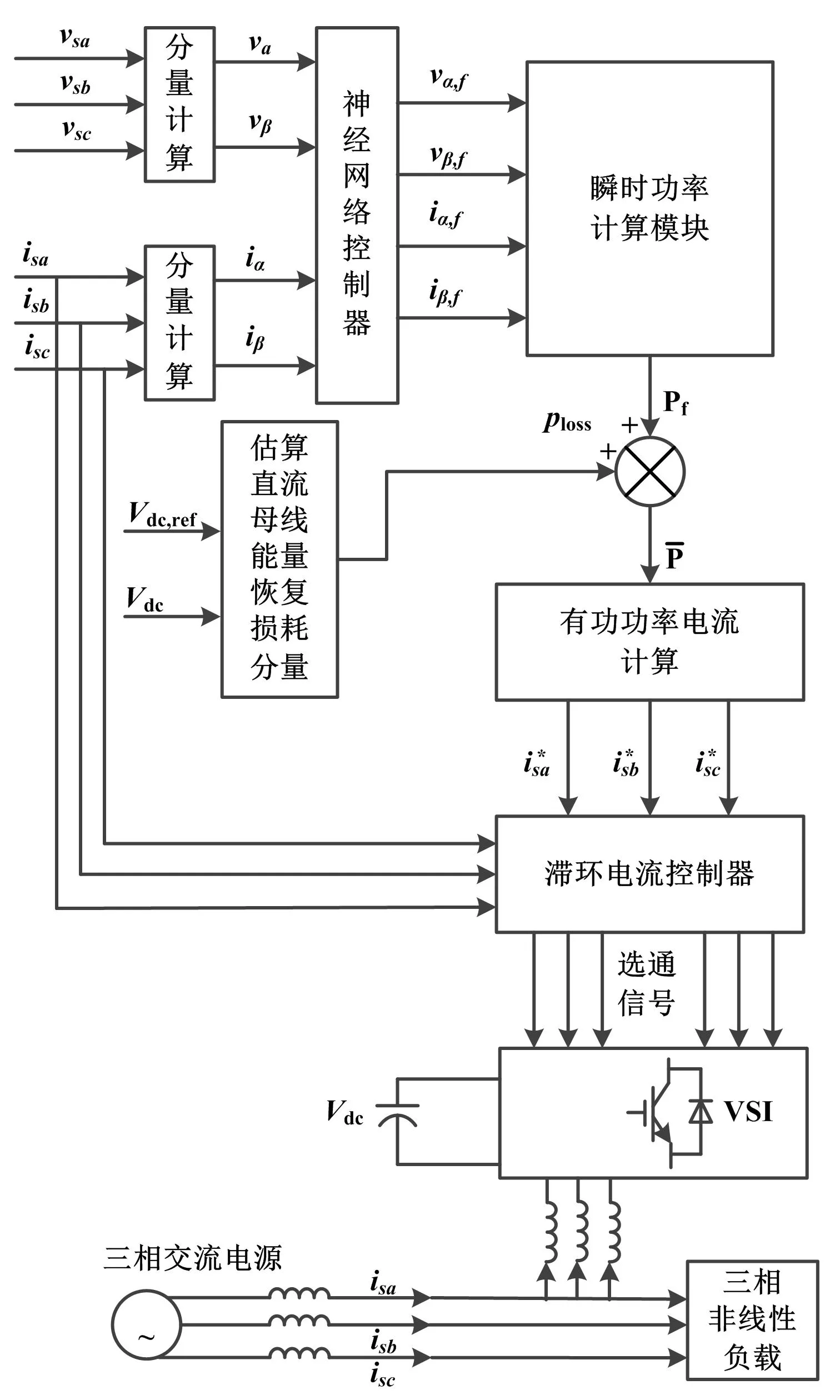
图3 控制方案框图Fig.3 Block diagram of control scheme

首先，进行三相到两相的变换。然后，利用模糊规则从电压和电流信号中提取基波分量，进而计算电源和负载之间的实际功率交换。即使在电源发生畸变的情况下，基波分量的提取也能快速、准确。该电源不仅提供负载电流的有功功率分量，还提供电流的损耗分量，使直流母线电容器的平均电压保持恒定。电源电流的这个损耗分量在稳态条件下供给逆变器电桥中的损耗，如开关损耗、电容器的泄漏电流等，并在施加于系统的瞬态条件下调节有源电力滤波器直流母线上的储能。该功率分量通过平均直流母线电压(Vdc)和所需的直流母线电压参考值(Vdc,ref)来计算。式(6)显示了电源的净实际功率，即基本实际功率和少量损耗功率之和。

(6)

供电系统应仅提供上述衍生电源。因此，CC-VSI的α-β参考电源电流表示为：

(7)

(8)

(9)

针对有源电力滤波器三相感应电流和参考电流的电流误差，采用基于PLL规则的无载波PWM电流控制技术，将选通信号传输到VSI桥的IGBT。有源电力滤波器从交流电源中提取所需电流，以供给谐波和无功电流，并在所有运行条件下产生正弦单位功率因数供电电流。

3 自适应神经网络逻辑控制器

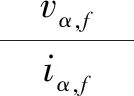
自适应神经网络[11]的结构为一个典型的两层(输入和输出)网络，包括n个输入和一个输出。该网络的基本模块是输入信号延迟向量、线性传递函数、权值矩阵和偏差。因此，输入和输出可描述为：

(10)

式中：b为偏差；wn为权重；in为网络输入；N为网络节点个数。

此外，由于网络的输入受信号的时间延迟序列影响，且考虑到预期的最大失真和三相输入信号的不平衡，故取N=61；网络系统的输入为电源电压和电流，输出为有源电力滤波器参考电流。

神经网络的控制器结构如图4所示。

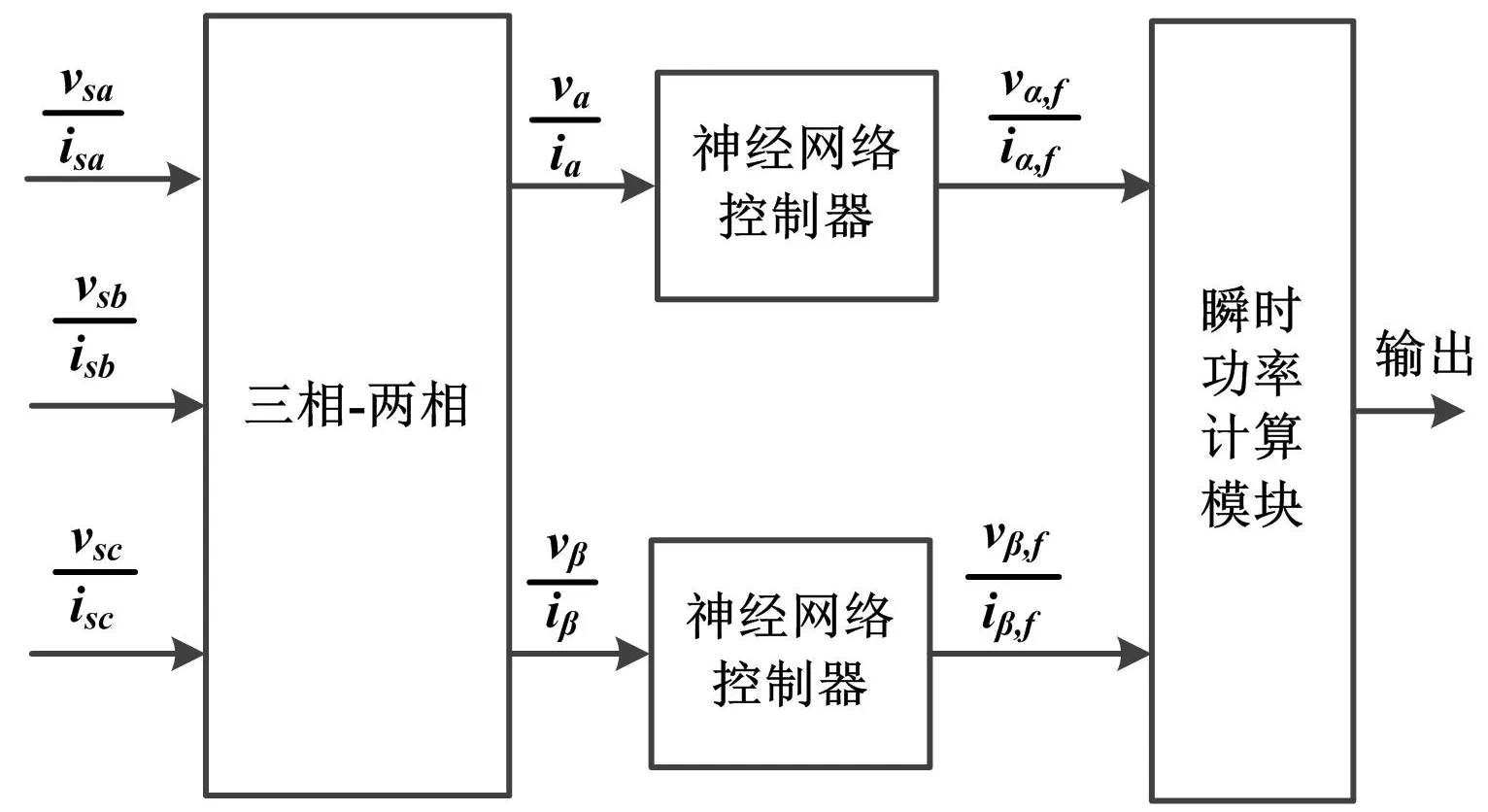
图4 神经网络的控制器结构Fig.4 Controller structure for neural networks

为确保训练效率，自适应神经网络在训练过程中使用Widrow-Hoff规则进行权值调整。通过重复训练，期望输出与实际输出的均方误差减小到3.2×10-5，学习率为0.000 6。

4 仿真及分析

为了对基于神经网络的有源电力滤波器进行仿真，本节在Matlab中Simulink TM模块下建立了仿真模型。整个有源滤波系统由三相电源、PWM电压型逆变器和带三相二极管整流器的R-L负载组成。

系统动态性能如图5所示。图5显示了在t=0.34 s时，负载突然增加和减少，负载平衡和不平衡时APF控制方案和系统的动态性能。此外，APF滤波器在0.30 s时打开。由图5可知：电源电流总谐波失真由28%降低到2.68%；在负载不平衡的情况下，电源电流的总谐波失真度约为2.3%，负载电流的总谐波失真度约为29%。仿真结果证明了控制器的性能和基准生成的准确性。

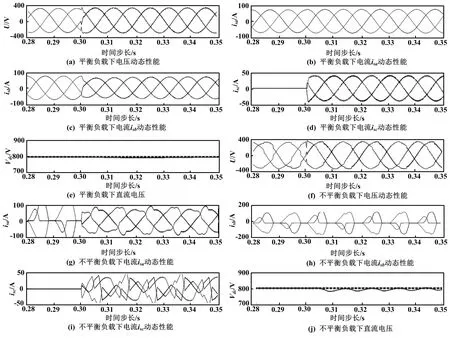
图5 系统动态性能Fig.5 Dynamic system performance

不同方法及总谐波失真值如图6所示。图6(a)和图6(b)所示为采用传统LPF方法和本文所提自适应神经网络控制方法总谐波失真(total harmonic distortion，THD)对比结果。可以看出，在电源电压畸变的情况下，THD由19.74%降低为2.41%。电压信号的输入分量失真，而神经网络控制的输出分量是基频为50 Hz的纯正弦。采用LPF控制时，电源电流波形不是正弦的。因此，本文所提方法具有良好的谐波抑制效果。

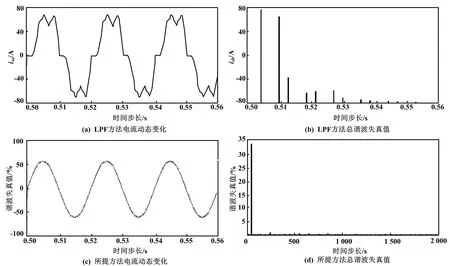
图6 不同方法及总谐波失真值Fig.6 Different methods and total harmonic distortion values

5 结论

本文设计了一种基于神经网络的鲁棒有源电力滤波方法，用于在平衡和不平衡的非线性负载类型和非理想供电电压条件下有效地补偿电流谐波和无功功率。神经网络控制性能的提高在仿真中得到了证明。该方案在系统相电压不对称和畸变的情况下也能较好地替代低通滤波器。所提出的方法能够在不需要无源滤波器的情况下提供补偿，并且能够在不考虑电源电压和负载电流条件的情况下保持补偿的源电流“正弦”和几乎“无失真”。