声激励液体透镜腔形状的模态仿真分析

霍明杰，石广丰，孟巳崴，姚 栋，梅毅杰，梁明波

(1.长春理工大学 机电工程学院， 长春 130022；2.深圳市大族思特科技有限公司， 广东 深圳 518103)

在日常生活中，透镜模块被电子器件大量使用，如智能手机、数码相机、智能机器人等[1-4]。传统变焦透镜一般由多组塑料、玻璃镜片组合在一起，利用齿轮在同一直线上不断调焦获得物体清晰的图像。液体变焦透镜根据设计原理分为基于液体折射率改变、电润湿液体接触角改变、液体表面曲率改变的液体透镜[5]。液体透镜具有响应速度快、轻便的优点。针对动态目标的观察，高速相机就显得尤为重要[6-11]。Koyama等[6]通过声辐射力作用的液体透镜仿真设计，得到双液体柱状腔高速变焦液体透镜。Jia等[12]在ANSYS中分析了3种不同边界约束下的等厚、不等厚薄膜透镜的情况，得到多焦点不等厚薄膜不规则柱形腔室液体透镜。Jones等[13]研发出一种偏振独立的半月形腔室电润湿液体透镜。Lpez等[14]研究发现谐波驱动毫米级柱状高速变焦液体透镜变焦规律。上述研究更多关注液体透镜的焦距、耗能等，没有关注液体透镜腔室的形状对液体透镜产生的影响。本文基于声激励液体透镜，分析液体透镜腔室形状对液滴表面的影响。

1 数值计算理论1.1 液滴平衡形态能量方程

液滴平衡形态能量方程为：

(1)

式中：σls为液固表面张力；σgs为气固表面张力；σlg为液气表面张力。

1.2 液滴自然频率控制方程

早期的毛细现象研究，有助于复原的表面张力被用来和弹性体比较，在忽略黏性的液滴中，Rayleigh研究得到黏性液滴振动的频率[15]。

(2)

式中：ωn为液体振荡频率；σ为表面张力；R为液滴的初始半径；ρi、ρe分别为内部流体和外部流体的密度；n为勒让德多项式对应模型形状的阶数。

1.3 液滴压强方程

在不考虑重力的情况下，利用矢量和速度势得到液滴压强计算公式[15]:

(3)

(4)

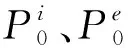
2 锥形腔室仿真前处理

2.1 液体透镜三维模型

通过对液体透镜结构的简化，利用三维建模软件SolidWorks构造0°、5°、10°、15°张口角度下的液体透镜模型(图1)。透镜模型由上下Polydimethylsiloxane(PDMS)膜，铝质腔壳，腔内的水组成。PDMS膜的厚度取相应半球形液滴半径的4%[16]，薄膜产生变形时，薄膜前后表面挠度差量为零[3]，模型的具体参数见表1。

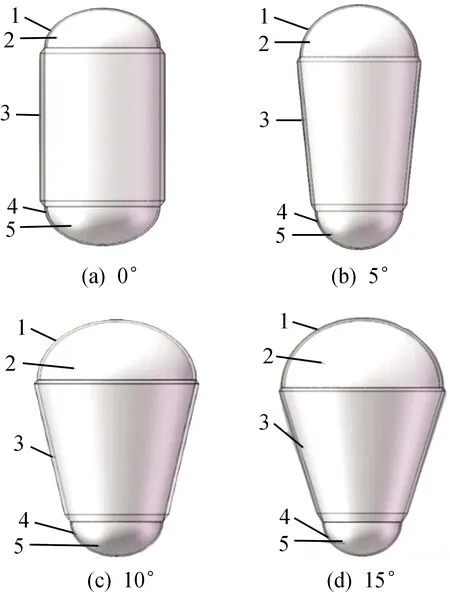
1-上薄膜；2-上球冠；3-铝质腔壳；4-下薄膜；5-下球冠

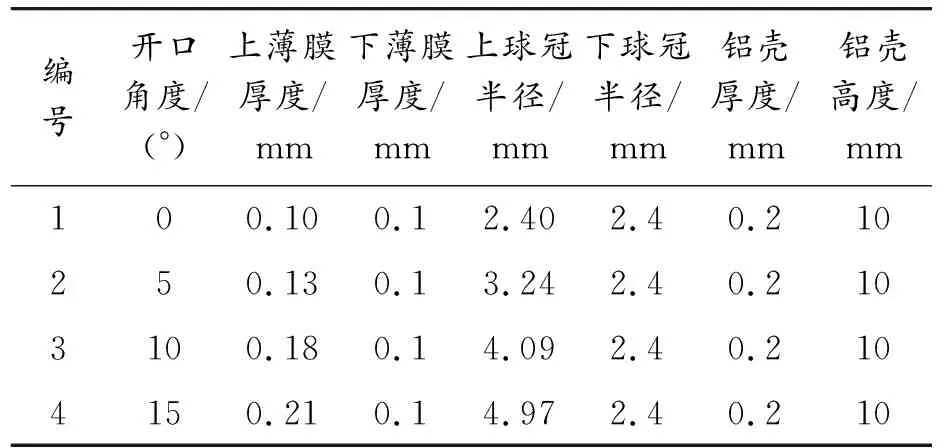
表1 不同张口角度液体透镜模型基本参数

2.2 网格划分

在COMSOL中导入1-4号模型，分别进行自由四面体细化网格划分，网格模型如图2所示。

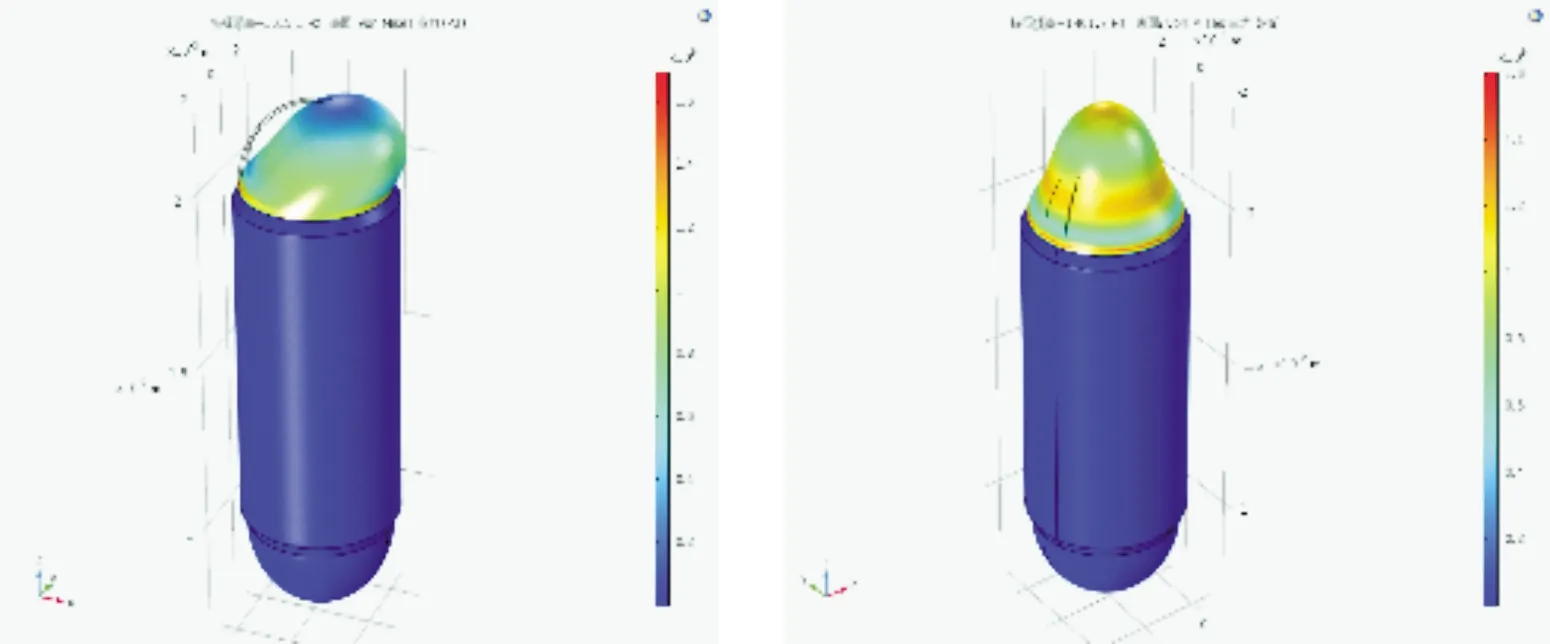
图2 不同张口角度液体透镜网格模型

2.3 边界条件设置

COMSOL多物理场仿真软件能很好的计算、模拟、仿真多物理场耦合下的物理现象，具有大规模计算能力和强大的前后处理功能。将网格模型导入三维声固相互作用，选择压力声学，固体力学接口。固体力学中对铝质腔体的外周面、倒角面、PDMS薄膜与铝腔体的接触面添加固定约束。在COMSOL中设置域的物理参数，水域的主要物理参数是关于温度的变量，PDMS膜，铝(3003-H18)的主要参数[17]见表2。

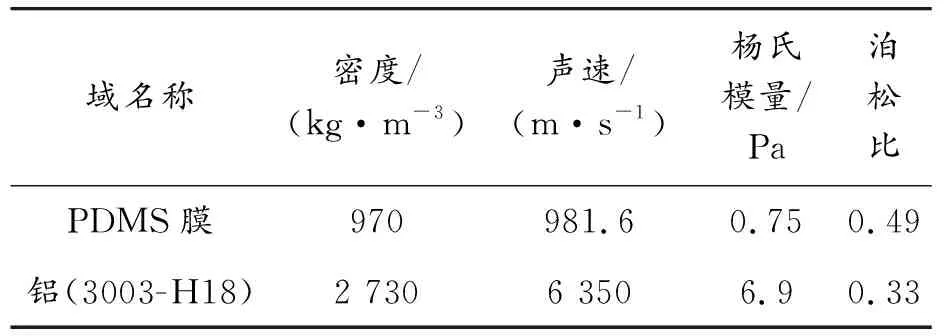
表2 PDMS域，铝的主要物理参数

3 液体透镜腔室仿真结果分析

3.1 液体透镜模型球冠面模态分析

球形谐波的指数(k，l)对仿真结果进行命名，利用式(4)得到波峰层数n与k，l的联系[18-22]。

(4)

式中：n为波峰层数；k为极波数；l为方位波数。

图3、4、5、6(n，l)模型中，(2，1)属于sectoral 模型，(4，0)，(6，0)属于zonal模型，(1，3)属于tesseral模型。在(2，1)模型中有2层波峰，一个偏轴向的隆起，(4，0)，(6，0)有4层和6层波峰，没有偏轴向的隆起，(1，3)模型中有1层波峰，3个均匀分布的隆起，呈“丫”字状。

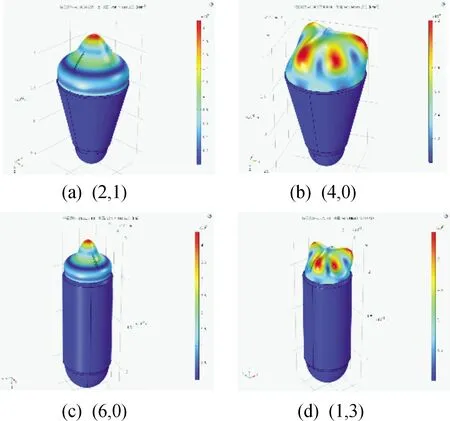
图3 0°液体透镜(n，l)模型

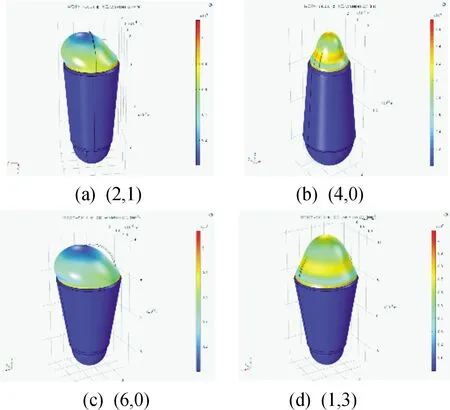
图4 5°液体透镜(n，l)模型

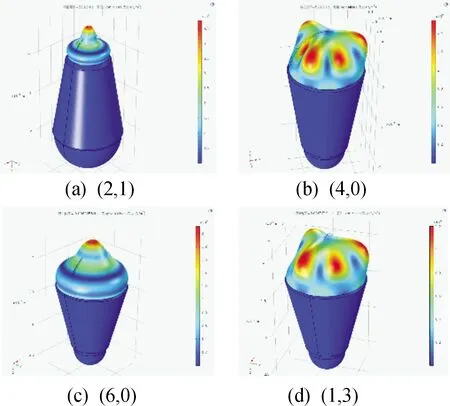
图5 10°液体透镜(n，l)模型

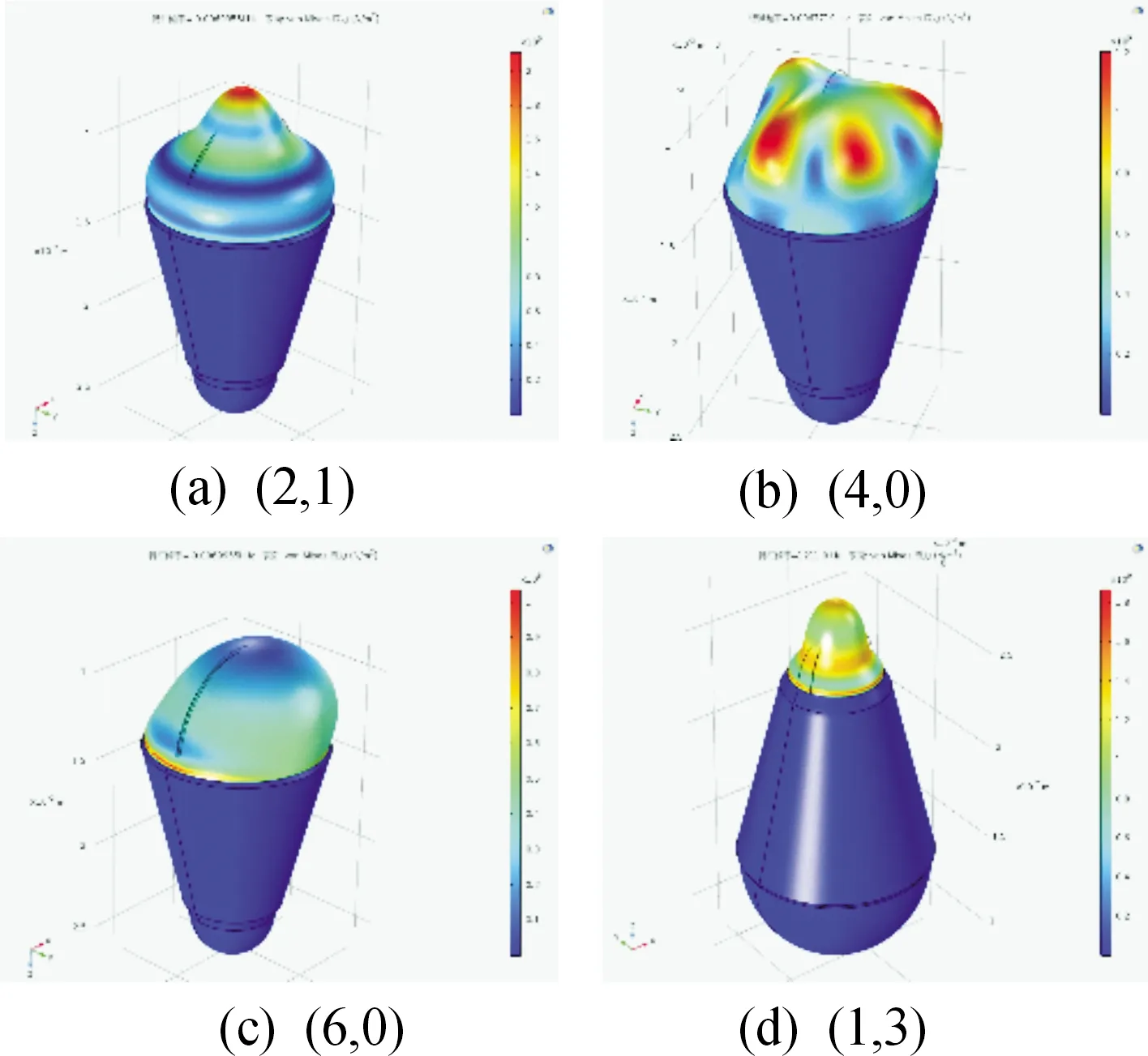
图6 15°液体透镜(n，l)模型

在(2，1)模型中，液体球冠偏轴向的隆起引起焦点变化，为液体渐进多焦点透镜的制造提供了良好的基础[23]。(4，0)，(6，0)模型中，液体表面曲率的变化引起正负焦距的变化，拓展了它的用途[24]。

3.2 液体透镜模型球冠面特征频率分析

图7、8、9中的(n，l)模型(2，1)，(4，0)，(1，3)，(6，0)对应于(k，l)模型(3，1)，(6，0)，(3，3)，(10，0)模型。在(k，l)模型中，当l=0属于zonal模型，k=l属于sectoral模型，k≠l属于tesseral模型。由图7可以得到(n，l)模型中(2，1)，(1，3)对应的(k，l)模型(3，1)，(3，3)随着张口角度的增加，模型的特征频率下降。对照图4、5、6中的模型，(2，1)，(1，3)模型中变形的球冠面都发生在液体透镜中较大球冠面。(n，l)模型(4，0)即(k，l)模型(6，0)，在图7中可以看到，液体透镜模型在张口角度0°至5°和10°至15°处出现了停滞和较大的增长，对照图4、5、6中的模型可以看到，(4，0)模型中的变形球冠面发生在液体透镜较小的球冠面。同理，从图7分析(n，l)模型(6，0)可以得到，液体透镜模型在10°的张口角度处，图4、5、6模型中的变形球冠面应该发生在较小球冠面。以上现象与自然频率计算结果一致。经过较多的试验研究，可以观察到，随着开口角度的增加tesseral模型更多的出现在液体透镜中较大的球冠面。

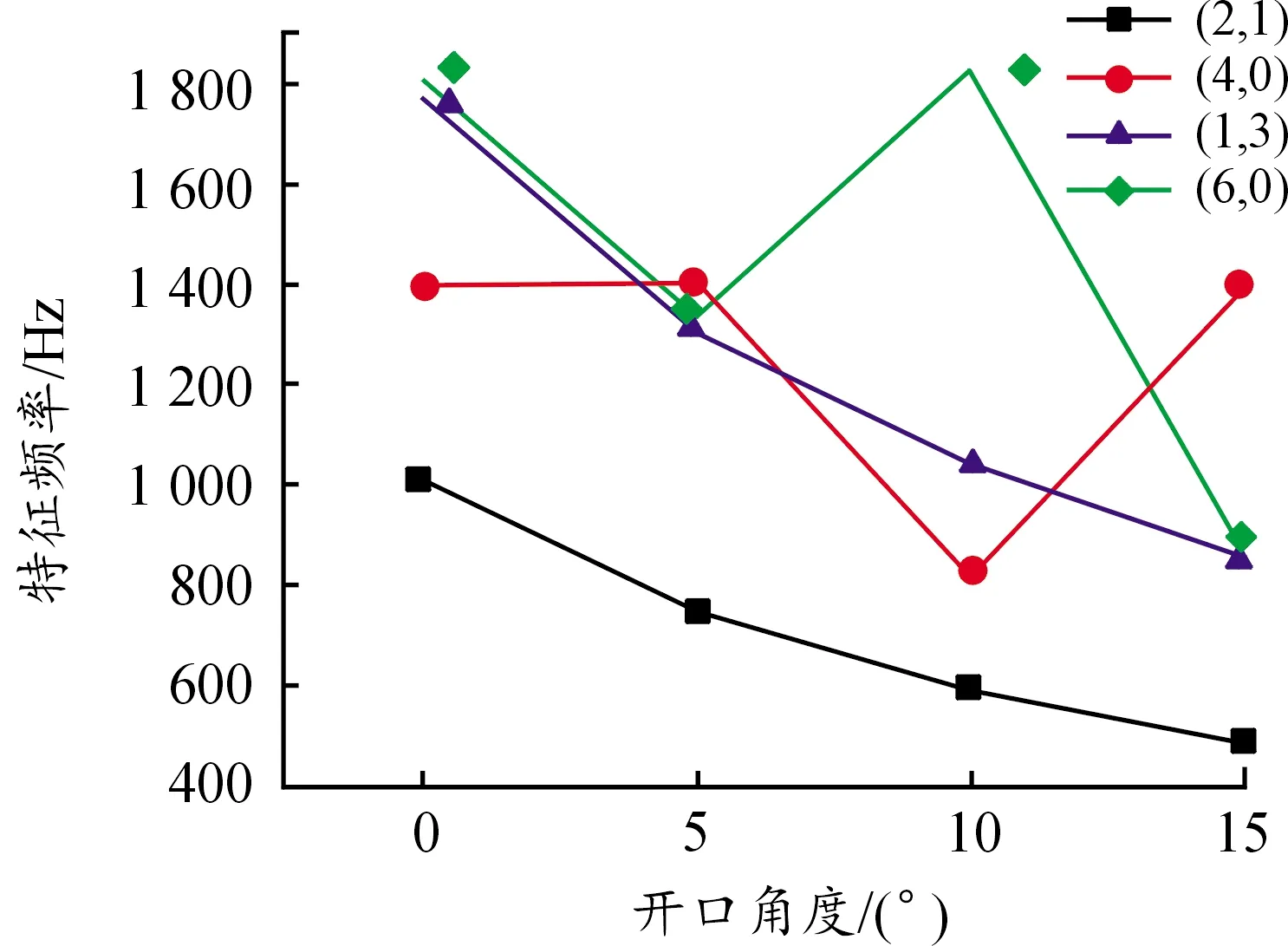
图7 4种模态中不同张口角度对特征频率的影响曲线

3.3 液体透镜模型球冠面应力分析

从图8可以看到(n，l)模型(2，1)，(1，3)随着开口角度的增加，液体球冠表面的最大应力值逐渐减小，对照液体透镜模型图可以发现，图3～6中发生变形的液体球冠面直径依次增加。(n，l)模型(4，0)在0°到5°的变化中，随着开口角度的增加，最大应力值出现了较小幅度的增加；5°到10°的变化中，最大应力值出现较小幅度的减小；10°到15° 的变化中，最大应力值发生较大幅度的增加。观察图4～6，发现5°、10°时液体球冠面的变形发生在较小球冠面，15°时发生在较大的球冠面。同理，研究(n，l)模型(6，0)发现在液体透镜模型张口角从5°变化到10°时，图8中最大应力值出现了较大幅度的增加，对照图4～6发现，液体张口角10°时，液体球冠面的变形发生在较小的球冠面。

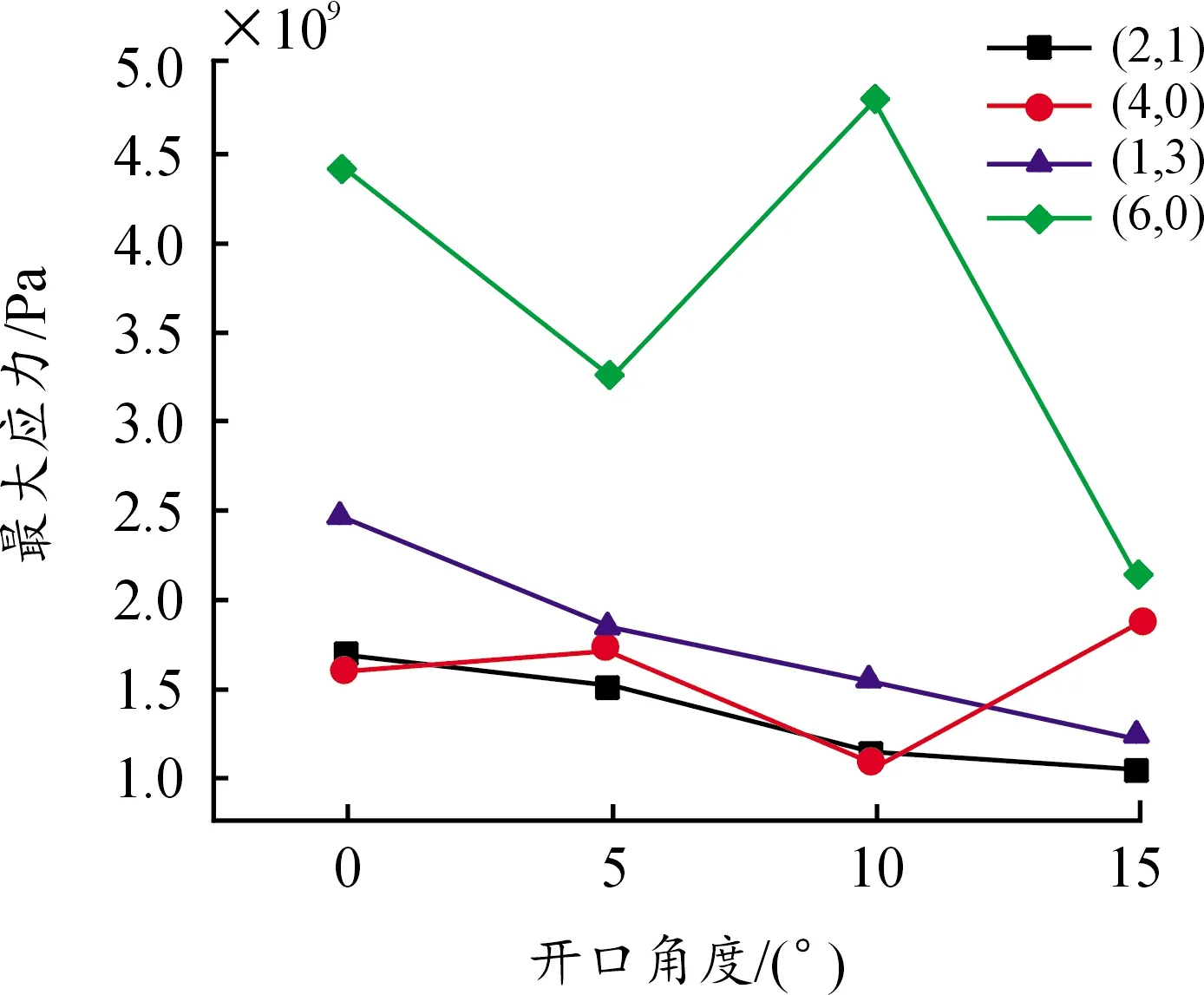
图8 4种模态中不同张口角度对最大应力的影响曲线

图9中可以看到，最小应力在(n，l)模型中的(2，1)，(4，0)模型发生了较小的浮动变化，而(1，3)，(6，0)模型在液体透镜模型张口角度从0°到5°时发生了较小范围的增加，5°变化为10°时,都发生了较大幅度的增加。对照图4、5、6发现，(n，l)模型(6，0)在液体透镜模型张口角度10°时，液体球冠面的变形发生在液体透镜模型较小的液体球冠面上，(n，l)模型(1，3)在液体透镜模型中没有表现出较大的模态特征。(n，l)模型(2，1)随着张口角度从0°到5°、10°、15°的变化，最小应力值依次减小。(n，l)模型(4，0)在液体透镜模型张口角度从0°变化到5°时，最小应力值出现了较大幅度的增加，5°到10°、15°变化时，最小应力值依次减小。

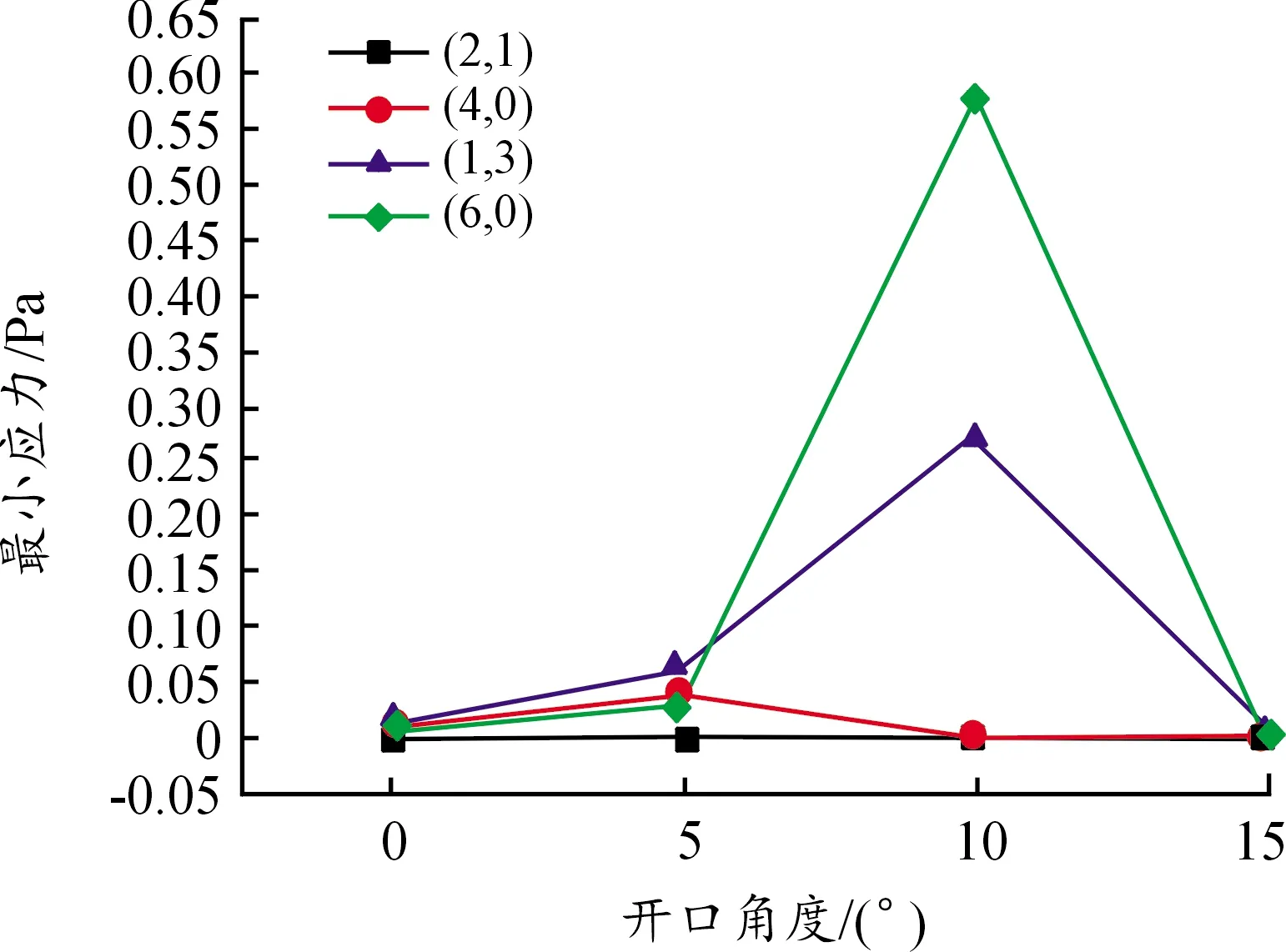
图9 4种模态中不同张口角度对最小应力的影响曲线

4 结论

1) 当液体透镜模型不存在张口角度时，zonal、sectoral、tesseral模型会交替出现在液体透镜模型的液体球冠面，其中tesseral在3种模型数目中占较大的比例。当液体透镜模型存在张口角度时，zonal、sectoral会交替出现在液体透镜模型的液体球冠面，tesseral模型更多的出现在较大球冠面，较小球冠面几乎不会出现tesseral模型。

2) 随着毛细锥形腔张口角度的增加，当液体球冠变形发生在较大球冠面上，液体球冠变形中的sectoral和tesseral模型对应的液体透镜模型的特征频率减小，液体球冠面最大应力减小，zonal模型已经出现在张口角度较小的液体透镜模型中的较大球冠面，在较小的球冠面再次出现时，特征频率会停滞或增加，液体球冠面的最大应力会增加，有利于选择合适的倾角降低能量消耗。

3) 随着毛细锥形腔张口角度的增加，液体球冠变形发生在较大的球冠面上时，液体球冠变形的tesseral模型最小应力减小。