涡扇发动机内外涵道水量分布比例数值仿真
2022-10-13薛文鹏宋江涛张琦
薛文鹏,宋江涛,张琦
(中国飞行试验研究院,西安 710089)
0 引言
航空发动机可能会在不同的环境条件下运行,即使在恶劣的天气条件下,也需要保障其安全和可靠地工作。雨天时,气流中的液态水会对发动机的性能和操作性产生不利影响。对于涡扇发动机而言,进入核心机的水会直接影响发动机的工作稳定性和性能,而吸雨考核也是发动机交付使用前必须进行的试验项目。一般为节省试验成本和降低试验风险,在发动机吸雨考核试验前需进行发动机吸雨仿真计算,以确定吸雨对发动机的影响,而内外涵道水量分配的确定(或进入内涵的水量)是进行发动机吸雨仿真计算中的关键,因此需对发动机吸雨状态下进入核心机的水量比例进行分析研究。
发动机在吸雨状态时,大量的雨滴撞击风扇,产生飞溅、扩散或反弹。Roumeliotis等研究表明,大约20%的水量撞击在进气锥的外表面,一部分液滴附着在叶片表面并形成水膜。对于风扇转子,旋转产生的较小液滴由于其惯性较小而随着气流进入外涵道。此外,撞击产生的部分二次液滴继续撞击转子叶片,产生更小的液滴。液滴与液滴、液滴与壁面碰撞以及风扇旋转导致外涵道和核心机之间的水重新分布。国外对航空发动机吸入雨水的研究较为成熟;Murthy等建立了航空发动机吸雨后对发动机特性的影响及各截面参数的变化规律;Schmehl等对工业燃气轮机中液滴的飞溅过程进行了研究,建立了1个基于经验数据的修正公式,以评估液滴与壁碰撞后产生的液滴直径;Nikolaidis采用3维建模仿真的方法研究不同转速下叶片形成水膜的厚度;Rajmohan等研究了不同吸雨量对发动机排气组分浓度的影响;Kaushik等采用数值计算的方法进行液滴直径轨迹追踪,将液滴直径看作质子,并未考虑碰撞、传热等对液滴轨迹的影响。中国学者对发动机吸雨的研究主要集中在吸雨对发动机的性能影响方面;李一光在航空发动机稳态性能模拟技术基础上,结合水的物理性质,采用数值方法研究了某双转子涡喷发动机吞水后的性能变化过程;陈光等总结了CFM56-3发动机投入使用后出现的一些吞雨停车故障,并提出了在发动机设计中采取的尽量减少雨水流入内涵的4点措施,介绍了喷水增大推力的机理和其在一些军民用飞机发动机上的应用情况;邢洋等按照GJB 241A的要求,进行了发动机地面吸雨试验,并结合试验数据分析了吸雨对发动机性能的影响。上述文献对发动机吸雨的研究均集中在发动机整机性能的变化方面,对发动机吸入雨水后雨滴在压气机内部的变化过程涉及较少,且未计算吸入雨水在叶片旋转和碰撞作用下水量在内外涵道的分配比例。
本文通过欧拉-拉格朗日法建立了两相流模型,研究了不同水气比、初始液滴直径和风扇转速对内外涵道水分分配比例的影响。
1 发动机吸雨现象
1.1 集雨系数
飞行条件对进入发动机的水浓度有显著的影响。在发动机低转速和高飞行速度(空慢下降)时,发动机捕获空气流管面积小于发动机进口几何面积,风扇进口截面的水浓度显著增加,高于大气环境的水浓度,这种现象称为集雨现象。为了表征集雨现象对风扇进口截面的水浓度影响,定义集雨系数为

式中:为发动机进口几何面积;为空气捕获流管面积。
发动机吸雨适航认证试验的最大水浓度为20 g/m,约等于3%的水气比。然而,欧洲航空安全局(European Aviation Safety Agency,EASA)提出了4%的水气比作为最大值来补偿因集雨现象引起的风扇进口截面的水浓度。
1.2 液液滴破碎
液滴在气-液两相流动中移动,由于速度差异,液滴可能会破裂,形成更小的液滴。液滴破裂高度依赖于气动力和液体表面张力,液滴破裂过程如图1所示。
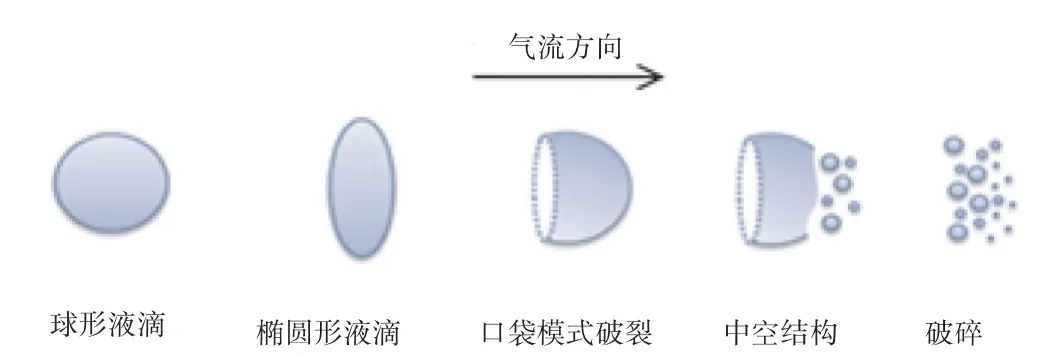
图1 液滴破裂过程
液滴破裂由韦伯数来确定,对于球形液滴,韦伯数和奥内佐格数定义为
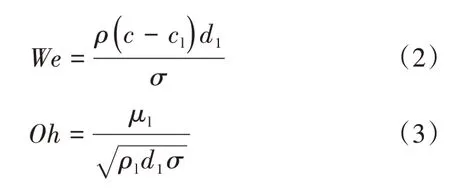
式中:为气流密度;为初始液滴的密度;为液体的速度;为气流速度;为初始液滴直径;为液滴的黏性系数;为液滴的表面张力系数。
液滴韦伯数表示气动力与表面张力之间的关系,而奥内佐格数表示液滴黏度的影响。表面张力对液滴的凝聚性很重要。如果超过临界韦伯数,则发生特定的破碎机制。若干学者分析了不同条件下液滴破裂的机理,所制定的液滴破碎准则见表1。

表1 液滴破碎准则
1.3 液滴与液滴和液滴与壁面的碰撞
发动机在吸雨时,气流中的液滴会产生液滴与液滴之间相互碰撞、液滴与发动机部件的碰撞。液滴与液滴、液滴与壁面碰撞会产生更小的二次液滴。
液滴与固体避面的碰撞如图2所示。图中,为碰撞后的二次液滴直径液滴与壁面碰撞后一般产生3种情形:液滴与固体壁面碰撞后附着形成液膜(附着)、反弹并保持其初始液滴尺寸(反弹)和破碎成较小的液滴重新进入气流(飞溅)。飞溅过程取决于液滴的初始尺寸、速度、风扇速度和液滴与风扇的相对位置。
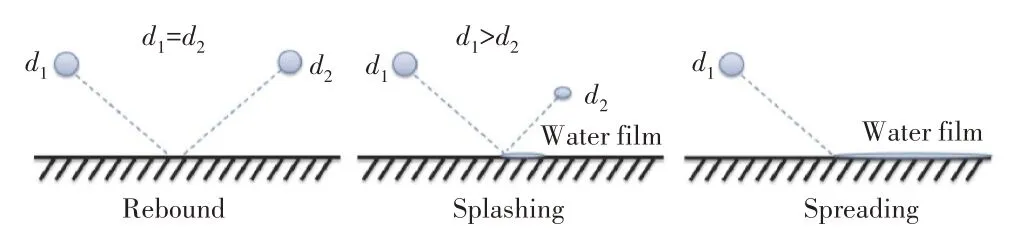
图2 液滴与固体避面的碰撞
1.4 水膜的形成
如果液滴发生飞溅,则产生更小的二次液滴,并在壁面上形成液体水膜。水膜在离心力作用下可能会沿着径向向外涵道流动。DAS等对压气机转子叶片上的水膜形成进行了数值研究,表明当含水量大于2%时,会在叶片压力表面上形成水膜。叶片上的水膜形成相当于增加了叶片的截面厚度,导致压气机的效率降低。
2 两相流模型
航空发动机的雨水吸入流动过程包括连续相(空气相)和离散相(液滴相),为了处理离散相和连续相的流动过程,本文采用两相流耦合算法进行计算。目前在两相流的计算中广泛应用的计算方法为欧拉法和拉格朗日法,如图3所示。欧拉法将携带气体和液滴作为1个连续体处理。在这种情况下,两相流在每个时间步长上都由热力学和流体力学状态变量来描述。假设流体是1个连续体,在1个平稳的参考框架中导出了基本的运动方程。而拉格朗日法中的液滴是在1个移动的参考框架中计算的,液滴和连续相是相互作用的。欧拉法分别计算每个液滴的轨迹,导致需要求解的方程数量增加;而欧拉-拉格朗日法将液滴分组为有限数量的液滴组,每组的轨迹表示流场中的一部分液滴。本文为了减少计算时间,采用欧拉-拉格朗日法进行液滴轨迹的计算。
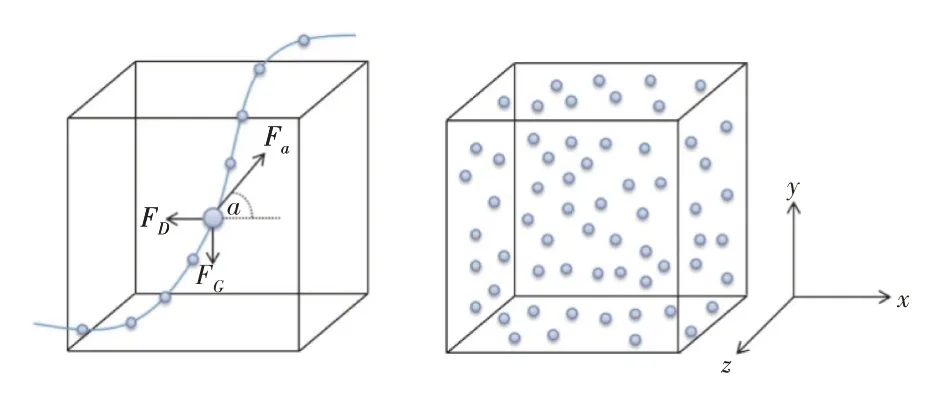
图3 欧拉法和拉格朗日法
在发动机吸雨过程中,液滴在气流中的运动过程可以通过液滴的受力情况进行研究。液滴受到作用力包括重力、拖曳力和离心力。因液滴与气流之间存在相对滑移速度,则液滴二者之间的拖曳力可以根据相对运行速度确定,因此液滴速度的变化可表示为

式中:为液滴和气流之间因滑移速度而产生的附加拖曳力;为液滴受到的离心力;为重力加速度。

式中:为拖曳力系数。
根据Young提出的液滴相在气流中运动的拖曳力计算方法,液滴在气流中运动的拖曳力系数可表示为
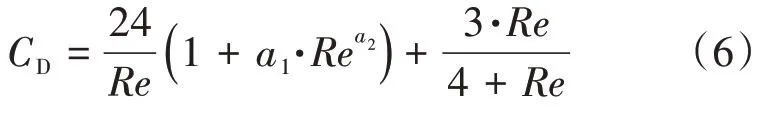
液滴的雷诺数为
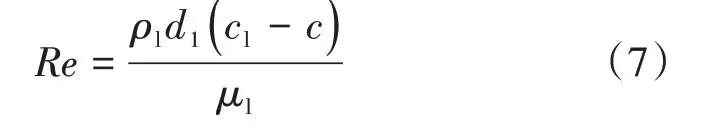
式中:、为液滴拖曳力修正系数。
液滴在离心力作用下产生径向速度,使液滴向沿着径向向外壁面移动。
3 数值仿真
本文对涡扇发动机风扇进行了数值仿真。风扇的几何模型(如图4所示)包括进气锥、分离器和转子叶片。考虑到风扇的几何对称性,为了减少计算时间,只对30°的截断进行了建模,进口条件为干空气和液滴组成的两相流。对不同的初始液滴直径、水空气比和风扇转速进行了数值计算。
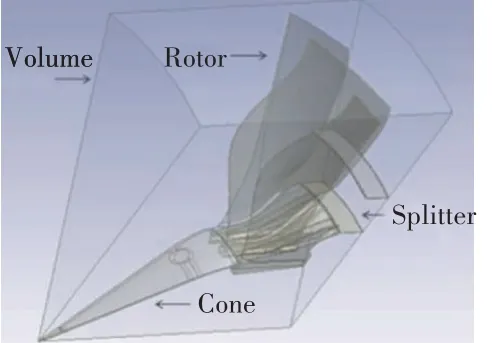
图4 风扇几何模型
利用-湍流模型对风扇的流场进行仿真计算。液滴相在进口截面均匀分布,压力为101325 Pa,温度为300 K,湍流强度值为1(中等强度),采用破碎模型计算液滴与液滴和液滴与壁面碰撞以及由此产生的二次液滴。进气锥和分离器采用六面体网格划分,计算收敛速度快。因风扇转子几何形状更复杂,采用多面体网格划分,网格总数为10。
4 仿真结果分析
采用上述模型计算了不同水气比、风扇转速和初始液滴直径条件下的水量分离比例。进入核心机和外涵道的水量分布表示为

式中:S为进入外涵道的水量比例;为进入核心机的含水量;为进入发动机的含水量;̇进入发动机中水的质量;̇为进入发动机空气的质量。
在水气比=1%、5%、10%,发动机转速=60%,初始液滴直径=1 mm的进口条件下进行水量分配计算,结果见表2。计算结果表明,随着含水量的增加,水量分离比例S略有增大。含水量从1%增大到10%,水量分离比例增大0.5%。液滴与液滴碰撞随着水浓度的增大而增强,并产生较小的液滴。液滴与液滴碰撞导致液滴直径从原来的=1 mm减小到=0.89 mm,当水气比增大到10%时,二次液滴直径减小到=0.62 mm,由于较小的液滴的惯性也较小,导致产生较大的水量分离比例。计算结果表明,初始含水量对水量分离比例的影响较小。
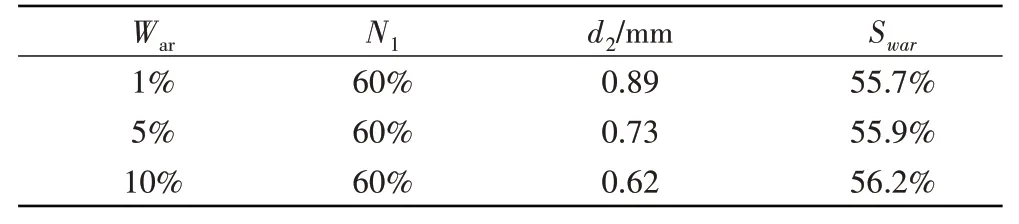
表2 水量分配比例
4.1 风扇转速影响
在风扇转速=60%、70%、80%、90%、100%时,计算在相同初始液滴直径下水量分配比例S的变化,仿真结果显示,风扇转速对分离水量有显著影响。初始液滴直径为3 mm、含水量为4%时,=60%、100%的径向水量分布如图5所示。从图中可见,当风扇转速从60%提高到100%时,进入核心机的从1.33%减小到1.14%,风扇转速越高,离心力越大,导致进入外涵道的水分比例增大。此外,对于高风扇速度,分离的水大部分聚集在叶片的尖端区域(图5(b))。

图5 风扇转速为60%和100%时的径向水分分布
进入外涵道的水量比例S随风扇转速的变化如图6所示。从图中可见,在所有初始液滴直径(1~5 mm)范围内,风扇速度与分离水量之间存在近似线性关系,且随着转速的升高,水量分离比例增大。
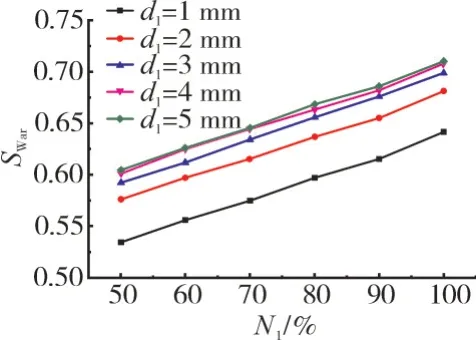
图6 进入外涵道的水量比例随风扇转速的变化(War=4%)
4.2 初始液滴直径的影响
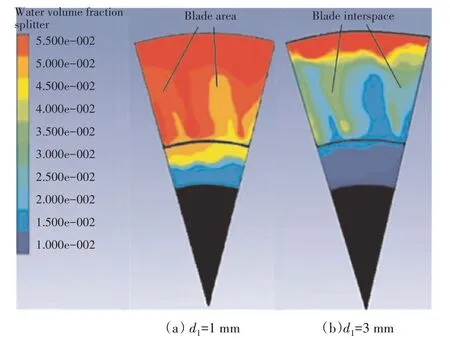
图7 d1=1、3 mm时的径向水分分布(War=4%,N1=60%)
为了确定液滴直径对水量分离比例的影响,对液滴直径为1~5 mm的液滴进行数值分析。水气比为4%、转速为60%时,=1、3 mm的径向水分分布如图7所示。从图中可见,初始液滴直径从1 mm增大到3 mm,进入核心机的水气比减小了0.64%。进入外涵道的水量比例随初始液滴直径的变化如图8所示。从图中可见,分离的水量随初始液滴直径的增大而增大,对于不同的液滴直径,其变化趋势一致。通常认为直径较大液滴的惯性也较大,因此需要较大的离心力才能改变原来的轨迹。但是较大的液滴碰撞后会产生较小尺寸的二次液滴,初始液滴直径越大,分离器入口平面上的二次液滴尺寸越小。较小液滴的惯性也较小,从而导致进入外涵道的水量增加。

图8 进入外涵道的水量比例随初始液滴直径的变化(War=4%)
4.3 进气锥表面的液膜
液滴撞击固体部件壁面形成液膜,一部分以液滴的形式重新进入气流,另一部分附着在固体表面。产生的液膜厚度取决于吸入水量、风扇转速和进气锥的几何形状。风扇速度为60%、水气比为4%时,进气锥表面的水膜厚度如图9所示。在进气锥正面,液膜厚度约为10 um。轴向方向,随着轴向位移的增加,液膜厚度减小;径向方向,随着半径的增大,液膜厚度减小。

图9 风扇进气锥上的水膜厚度(War=4%,d1=3 mm,N1=60%)
5 仿真结果验证
将仿真计算得到的二次液滴尺寸与文献中的数据进行比较。Schmehl等对工业燃气轮机中液滴的飞溅过程进行了研究,建立了1个基于经验数据的修正公式,以评估液滴和壁面碰撞后产生的液滴直径。
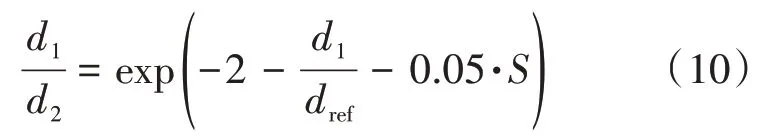
式中:为参考液滴直径;为飞溅参数。
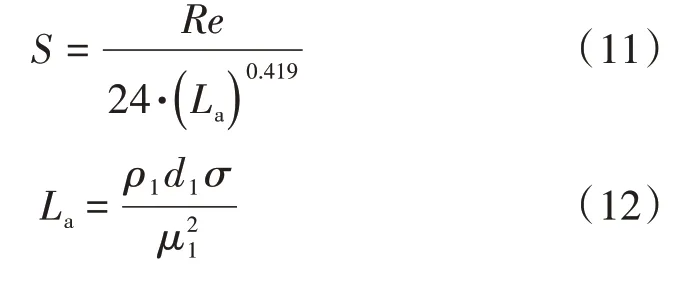
航空发动机与工业燃气轮机的工作原理一致,对于空气压缩部件而言,二者具有相似的气动结构和热力学过程,因此式(10)也适用于航空发动机。
飞溅参数用于判别液滴与壁面碰撞现象,碰撞现象与韦伯数的关系见表3。

表3 碰撞现象与韦伯数的关系
将二次液滴尺寸的仿真计算值与文献[6]中的数据进行比较(如图10所示),二者相关性均呈相同趋势。初始液滴直径越大,飞溅后的二次液滴尺寸越小。结果表明,飞溅后原液滴尺寸减小为原来的1/50~1/100。产生的二次液滴尺寸高度依赖于初始液滴速度。本文初始液滴速度为185 m/s,与飞机在颠簸气流中的典型飞行速度相当。

图10 仿真数据与文献[6]中的数据对比
为评估仿真结果与文献[6]的差异,定义仿真偏差
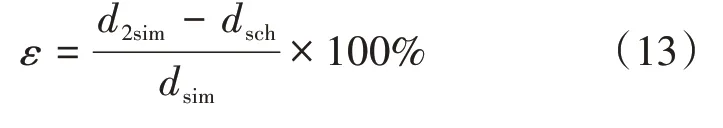
式中:为仿真计算得到的二次液滴直径;为文献[6]中的液滴直径。
二次液滴直径的仿真计算值与文献[6]中数据的偏差如图11所示。从图中可见,初始液滴直径为1 mm时偏差最大,为3.3%。
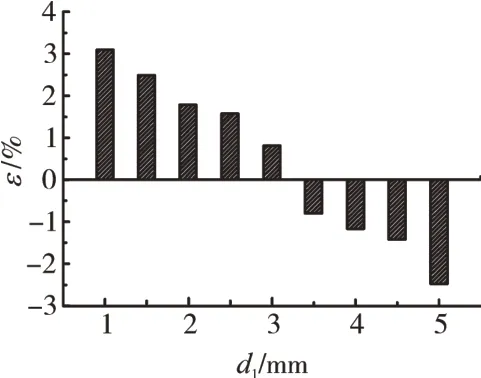
图11 仿真数据与文献[6]中的数据偏差
6 结论
(1)进入核心机的水量取决于液滴的初始液滴直径和风扇速度,含水量对进入核心机的水量影响较小。
(2)二次液滴直径的计算值与文献[6]中的数据相符合,最大误差为3.3%。
本文建立的试验仿真方法对计算液滴的内外涵道分配具有一定的参考价值。
