复杂路况下无人车辆全速域路径跟踪复合控制研究
2022-03-23黄迎港罗文广蓝红莉
黄迎港,罗文广,蓝红莉,陈 锴
(1.广西科技大学 电气与信息工程学院, 广西 柳州 545006;2.广西汽车零部件与整车技术重点实验室(广西科技大学), 广西 柳州 545006)
无人驾驶技术作为未来汽车的发展趋势——如何提高路径跟踪精度和控制器的鲁棒性,仍是当今的研究热点和难点。现有研究中,路径跟踪常见方法有PID、LQR、自抗扰算法、预瞄控制、模型预测控制和显式模型预测控制等。
PID控制是一种依靠误差量进行反馈控制的方法,为提高控制器的响应速度设计增量式PID控制策略[1],为解决PID参数在不同环境运行时需要反复调整的问题,构建自适应PID路径跟踪控制结构[2-3],提高跟踪控制器的鲁棒性。由于PID控制仅依靠运行时的误差信息,并未考虑车辆自身特性对控制器的影响,因此,陈亮等[4]考虑横向动力学特性对车辆的影响,采用LQR算法求解车轮侧偏力,通过刷子轮胎模型计算出前轮转角量,该方法仅适用于中低速下的路径跟踪;闫振争等[5]使用粒子群优化的自抗扰算法设计路径跟踪器,但PSO算法中粒子的种群趋同现象将导致寻优结果未必为全局最优解,将量子行为粒子群优化算法(QPSO)用于控制器参数选择,提高全局加权矩阵的寻优能力[6]。预瞄控制算法是基于几何关系设计的,实时性强,但预瞄距离限制了该方法的应用,因而,刁勤晴等[7]采用动态双预瞄点策略保证大曲率条件下车辆路径跟踪精度。模型预测控制(MPC)以其在处理非线性模型和多约束问题方面的优势,近年来在路径跟踪领域应用广泛。张会琪等[8]将输出量约束考虑到MPC控制器设计中,采用多约束模型预测控制器完成路径跟踪任务;刘英杰等[9]在分析汽车线控转向操纵模型的基础上提出MPC路径跟踪控制方法,该方法受预测时域影响较大,一般模型预测控制器参数多为定值,容易导致控制参数与实际道路环境不匹配,降低跟踪精度。在MPC路径跟踪控制器的基础上衍生出自适应变参数控制方法,解决权重系数及预测时域对跟踪效果影响的问题[10-12];考虑预测时域和速度对跟踪精度的影响,设计非线性MPC(NMPC)控制器,提高了车辆行驶的稳定性[13]。前视距离是影响纯追踪控制器稳定性和精确跟踪的关键参数,将变前视距离的纯追踪控制与MPC控制算法结合,根据横向误差设计切换逻辑解决横向偏差过大模型预测控制失效问题,但复杂环境下的驾驶适应性有待提高[14]。通过加入道路边界约束表征车辆实际行驶状态,防止车辆出现冲出路面现象的发生[15],刘凯等[16]考虑道路曲率和路面附着系数对车辆转向的影响,设计变步长离散化方法解决控制器实时性和跟踪精确性相矛盾问题,建立滑移和道路约束应用MPC算法求解控制量,但其仅考虑当前道路曲率对性能的影响,导致跟踪控制器对前方道路的预见性差。将实时性较强的显式MPC(EMPC)算法用于路径跟踪中可降低算法运行时长[17]。以上方法解决了无人车辆路径跟踪问题,并一定程度上提高了跟踪精度,但并未考虑高速行车情况,即未实现宽速度变化范围的路径跟踪。
针对上述问题,建立3自由度车辆误差状态方程,并对其进行离散化线性化,得到车辆状态误差预测模型,并对车辆行驶过程中动力学特性进行分析,建立车辆动力学和控制输入量约束,建立二次型性能指标,运用模型预测控制实时求解满足约束条件的控制量;在深入分析不同车速和路面附着系数对踪精度和车辆稳定性影响的基础上,将车辆横摆角误差与位置误差作为输入量,运用模糊控制进行转角补偿,并以道路曲率信息作为是否进行补偿的选择机制;二者共同构成无人驾驶车辆全速域路径跟踪复合控制器,以实现车辆宽速度变化范围下路径跟踪任务。
1 车辆模型
1.1 动力学模型
建立3自由度(纵向、侧向和横摆)车辆模型,如图1所示。在保证控制效果的基础上做出如下假设:① 车辆悬架系统为刚性连接,忽略其对转向系统的影响;② 忽略轮胎的横纵向耦合关系;③ 忽略车辆的Z轴运动,假设车辆行驶在水平道路上;④ 忽略空气动力学对车辆行驶造成的影响;⑤ 忽略轮距对车辆转弯半径的影响。
图1 3自由度车辆模型
图1中,Fxf、Fxr为车辆前后轮胎在x轴受力;Fyf、Fyr为车辆前后轮胎在y轴受力;lf、lr为车辆质心到前后轴的距离;Vx、Vy为车辆x、y方向车速;V为实际车速;φ为车辆横摆角;δf为前轮转角。xoy坐标系为车身坐标系,XOY坐标系为地球坐标系,坐标变换关系为:
(1)
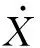
车辆动力学微分方程为:
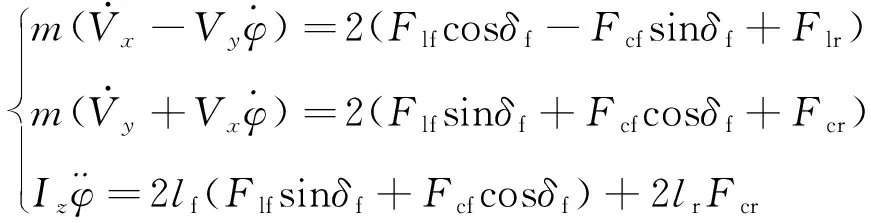
(2)
式中:Fcf、Fcr为车辆前后轮胎侧向力;Flf、Flr为车辆前后轮胎纵向力;m为车辆质量;Iz为车辆绕z轴的转动惯量。
车辆轮胎力为:
(3)
式中:Ccf、Ccr为前后轮胎侧偏刚度;Clf、Clr为前后轮胎纵向刚度;sf、sr为前后轮胎滑移率。
基于小角度假设简化式(2),即sin(δf)≈δf,sinα≈α,cos(δf)≈1,cosα≈1,并联立以上各式得车辆动力学方程:
(4)
1.2 误差模型
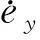
(5)
车辆的期望加速度为:
(6)
可得
(7)
(8)
eφ=φ-φt
(9)
代入式(4)可得车辆误差状态方程为:
(10)
2 全速域路径跟踪复合控制器
行车时除受自身动力学条件约束外,还受当前车速及地面附着系数变化的影响。表1为不同条件下常规的MPC控制器对双移线路径的跟踪效果。由表1可见,当道路附着系数为0.85时,随着车速的增加,横向误差越来越大,当车速增大到108 km/h时,车辆将失去跟踪能力,并出“画8”现象,控制器失效,路径跟踪失败;车速为72 km/h时,随着路面附着系数的降低,行驶横向误差值越来越大,当车辆行驶在μ=0.3时,车辆在刚入弯处由于转向不足导致车辆偏离目标轨迹,之后误差不断累积,在出弯道时最大横向误差达到1.753 m,车辆出现占道行驶。
显然,常规的MPC控制对低附着系数路面及高速行驶均不能实施良好的路径跟踪,甚至出现路径跟踪失败情况。MPC控制器无法满足复杂路况下无人驾驶车辆全速域跟踪精度要求。为了解决此问题,考虑模型预测控制反馈校正与模糊控制能克服非线性系统不确定性干扰的优点,提出无人驾驶车辆全速域路径跟踪复合控制方法,如图2所示。图中,u1为MPC控制器输出,u2为转角补偿控制器输出,将二者的输出加权得到当前时刻的车辆控制量。图中的“选择机制”用于选择何时投入转角补偿控制器。
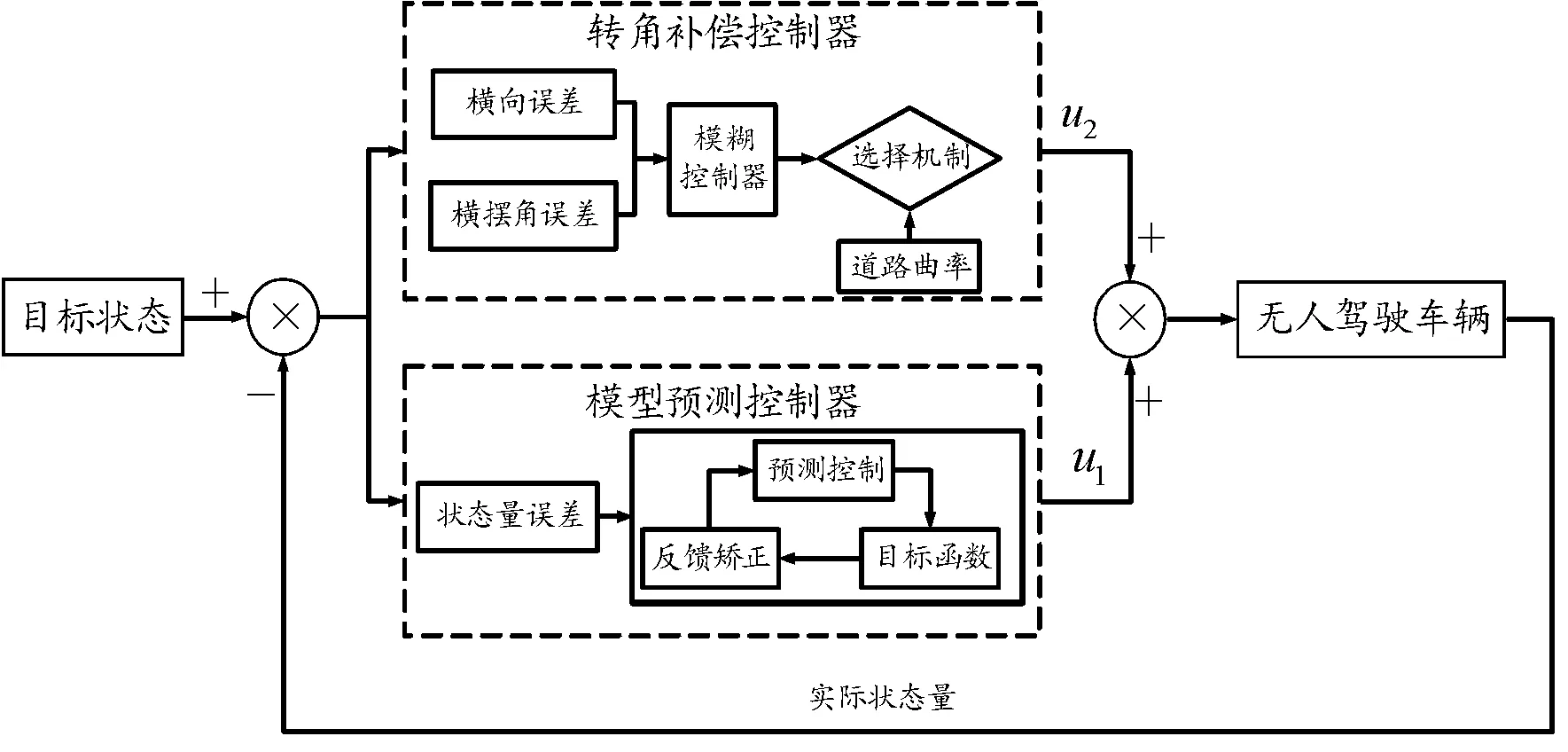
图2 无人驾驶车辆全速域路径跟踪复合控制框图
2.1 路径跟踪的模型预测控制器
对式(10)进行离散化处理,得:
ξ(k+1)=Akξ(k)+Bku
(11)
式中:Ak=I+ATs,Bk=BTs,Ts为采样时间。
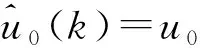
(12)
式(12)为非线性系统,直接用于预测模型计算量大,需对其进行线性化。在其工作点处进行泰勒级数展开:
(13)
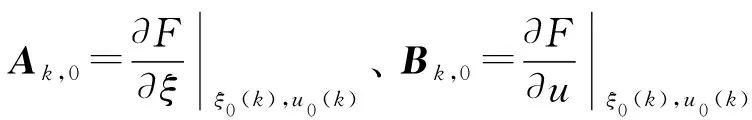
式(13)减去式(12):
ξ(k+1)=Ak,0ξ(k)+BVk,0u(k)+dk,0
(14)
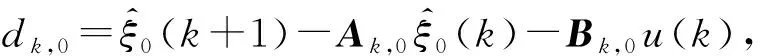
在每个采样时间的系统线性时变方程为:
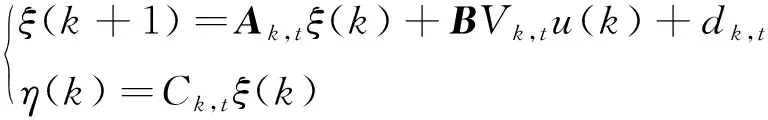
(15)
构造一新的状态变量
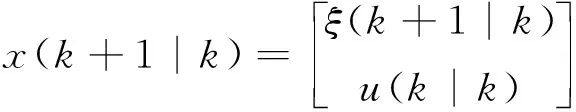
(16)
代入式(14)得新的状态空间表达式:
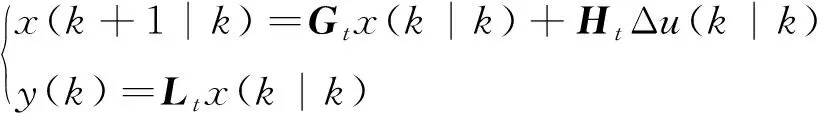
(17)
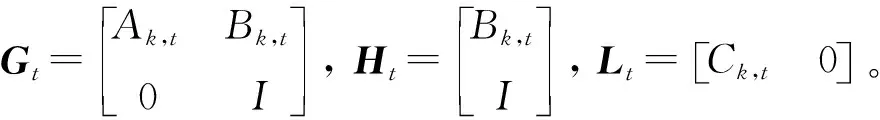
为便于计算,令控制时域外系统控制量不变,则每一时刻系统预测方程为:
Y(k)=χ(k)x(k|k)+ρ(k)ΔU(k)
(18)
式中:Np为预测时域;Nc为控制时域。
Y(k)= [y(k+1|k)y(k+2|k) …y(k+Np|k)]T
(19)
ΔU(k)= [ΔU(k|k) ΔU(k+1|k) … ΔU(k+Nc-1|k)]T
(20)
(21)
(22)
为满足控制器对车辆稳定性和响应快速性的设计要求,建立如下目标函数:
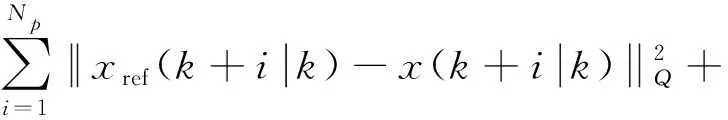
(23)
式中:Q、R、ρ为权重系数;ε为松弛因子,用于防止求解QP问题时找不到可行解。
从行车安全性和驾乘人员乘坐舒适性的角度出发,需对控制器的输入量和车辆动力学进行限制。
控制约束条件为:
umin(k)≤u(k)≤umax(k)
k=0,1,…,Nc-1
(24)
控制增量约束条件为:
Δumin(k)≤Δu(k)≤Δumax(k)
k=0,1,…,Nc-1
(25)
车辆轮胎侧偏力在±5°与轮胎侧偏角呈线性关系,考虑行车路面附着系数对轮胎摩擦力的影响,设前轮侧偏角约束为:
-3°≤β≤3°
(26)
车辆加速度约束为:
-0.4g≤a≤0.4g
(27)
k时刻控制量的矩阵形式为:
u(k)=u(k-1)+Δu(k)
(28)
设:
Ut=1Nc⊗u(k-1)
(29)
(30)
结合式(30)可得式(24)的矩阵形式,如下:
Umin≤AΔUt+Ut≤Umax
(31)
将式(23)转化为二次型目标函数,并结合约束条件式(31),构成路径跟踪优化问题。
通过以上分析,建立基于车辆误差状态空间方程的无人驾驶车辆路径跟踪模型预测控制器,求解该优化问题得到控制时域内的前轮转角及和纵向加速度控制量序列值,将第一组元素作为实际控制量,前轮转角实现对车辆的横向控制,纵向加速度实现对车辆转向过程中速度的控制,重复上述过程,完成车辆对期望轨迹的跟踪任务。
2.2 转角补偿控制器
无人驾驶车辆是高度非线性系统,并且模型预测控制器无法在线修改整定好的参数,这将降低其适应性和鲁棒性。模糊控制算法不依赖精确模型,能够对复杂系统进行控制。采用模糊控制原理对车辆行驶过程中的前轮转角量进行补偿,达到车辆稳定、快速准确地跟踪目标路径的效果。通过对车辆行驶状态的分析可知,跟踪效果与车辆的横向偏差、横摆角偏差以及道路的曲率有关,故将当前时刻的横向偏差与横摆角偏差作为模糊控制器的输入,前轮转角作为控制器的输出,设计转角补偿控制器。
定义输入输出变量的基本论域为[-3,3],为确保控制的灵敏度以及控制器的响应速度,选择5个模糊子集的语言变量,分别为[NB、NS、ZE、PS、PB],并选择三角形隶属度函数。模糊控制规则如表2所示。
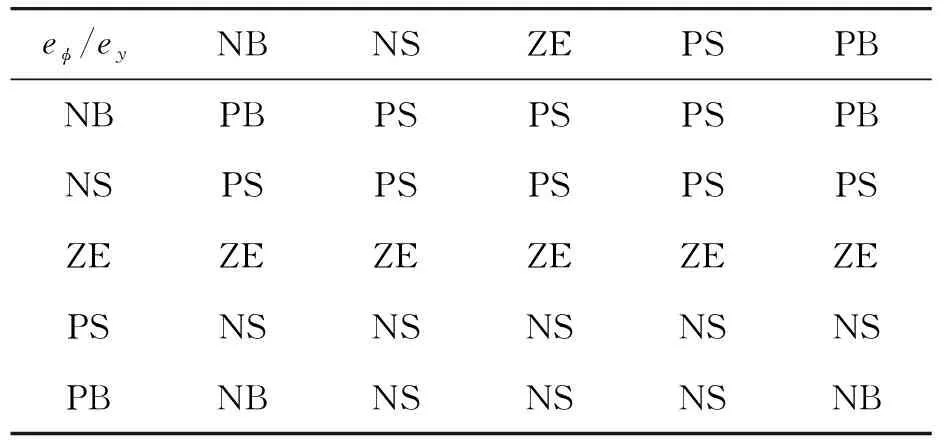
表2 模糊控制规则
模糊控制规则:保证路径偏差不超过最大允许值,同时满足车辆的舒适性和车辆稳定性要求。根据驾驶经验可知,当位置误差较大时,为了使车辆能够快速回到目标路径,减小跟踪偏差,应适当增大前轮转角,直到误差减小到允许范围内;当位置误差较小,横摆角误差较大时,为了使车辆有更好的稳定性,若位置误差保持在允许范围内则不进行控制,反之则使用小转角加以补偿,提高司乘人员的舒适性。
关于“选择机制”,前文分析表明,车辆直线行驶时MPC控制可实现目标路径的跟踪任务,而道路有弯道时可能会产生跟踪效果不佳或不能跟踪现象,为此选择道路曲率为是否引入转角补偿控制器的判断标准。通过V2X技术获得道路曲率信息,当曲率超出(0±0.05%)时,补偿控制器对MPC控制器前轮转角控制量进行补偿,提高弯道跟踪精度及连续弯道时的切换速度,避免转向不及时导致跟踪偏离问题的发生。
3 仿真实验和分析
为验证所提出方法的控制效果,搭建Simulink与Carsim联合仿真模型,并与预瞄控制器、纯追踪控制器、文献[8]方法以不同车速(36、72、180 km/h)在不同路况下进行对比仿真试验。
3.1 避障路径规划
无人驾驶车辆实际行驶环境未知,外部环境是复杂的、动态的,预设轨迹不一定满足实际行驶要求。要实现复杂路况下全速域跟踪控制,须加入避障规划模块,而传统的避障规划多基于安全距离设计,这仅仅适用于中低速情况。由于刹车距离与车速成正比,从兼顾高速行车防碰撞角度出发,提出一种考虑安全行车的避障路径规划方案。该方案由高精度地图(H_Map)提供前方的道路及障碍物信息,通过插值方法生成满足安全行车距离的防碰撞行驶路径,如图3所示。通过模拟生成双移线避障路径来同时测试路径跟踪控制器性能及路径重规划的有效性。
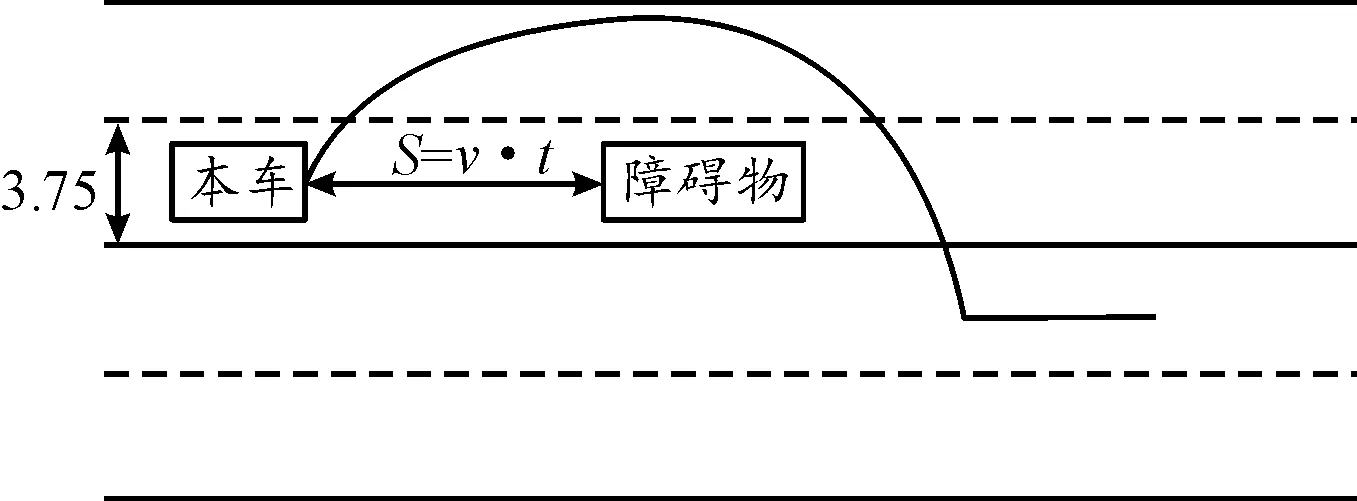
图3 避障路径规划示意图
安全行车距离与当前车速成正比,可得安全行车时间t1=s/v。据当前车速和最大制动减速度as=4 m/s2可计算出车辆紧急制动停止时间t2=v/as。人类神经反应时间t3为0.5 s。根据GB12676规定车辆制动生效时间t4最大为0.6 s,故车辆避障时应与前车保持的最小距离为s=v·(t1+t2+t3+t4)。仿真道路选用3.75 m宽的高速道路,车辆实际宽度约为1.9 m。假设车辆保持在车道中心线行驶,从安全角度考虑车辆行驶过程中的横向允许误差不应偏离目标路径0.9 m,即车辆不发生占道行驶现象,以实现安全范围内的路径跟踪。
3.2 相同路面附着系数下不同车速的路径跟踪实验
本节验证不同控制器在干燥路面(μ=0.85)、不同速度下的跟踪效果,无人驾驶车辆车速分别为36、72、180 km/h。由图4可见,车速为36 km/h时,所有控制器都可实现良好跟踪。当车速增大到72 km/h时,预瞄控制器由于连续转弯导致误差累积,在327 m处最大横向误差达到0.826 m,并且出现 “画8”现象;纯追踪控制器基本能实现跟踪,而文献[8]方法仍能够实现良好跟踪。当车速增大到180 km/h时,预瞄控制器在弯道后几乎不能实现跟踪;纯追踪控制器是依靠车辆与追踪点的几何关系而忽略车辆动力学特性设计的,导致在第一个弯道处转向不足,并在下一弯道处失去跟踪能力;文献[8]方法的跟踪误差在允许误差范围内,但在入弯处发生转向迟滞现象,导致直线行驶时未能行驶在路径中心线上,产生一定的跟踪误差。本文方法在72、180 km/h高速度下均能实现良好跟踪。
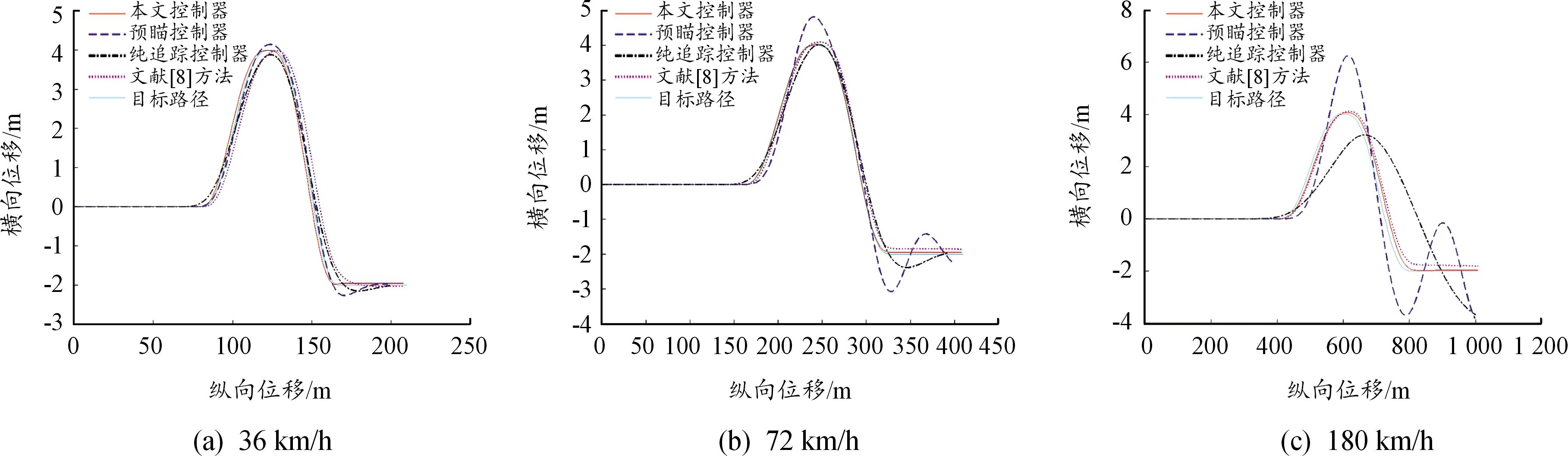
图4 车辆路径跟踪仿真结果
为了进一步说明本文方法性能的优越性,给出了各种控制方法的横摆角速度、侧向加速度和前轮转角仿真情况,如图5~7所示。可见,基于反馈控制方法设计的控制器(本文方法、文献[8]方法)优于基于转向几何方法设计的控制器(预瞄控制、纯追踪控制),且车辆各项参数均处在允许范围内,而后者在高速情况下不能完全满足车辆的稳定与舒适性要求。本文方法随着车速的增加,车辆的横摆角速度降低,有利于提高转向稳定性,降低侧翻现象发生概率(图5);能够将侧向加速度控制在±0.24g范围内,使轮胎侧偏特性始终保持在线性区域,提高了无人车辆的操纵稳定性、安全性与乘坐舒适性(图6);另外,由于加入转角补偿器,180 km/h行驶时会提前计算转角量,入弯后车辆转向角度会保持一段时间,换向时斜率更大,响应速度更快,且并未发生文献[8]方法中前轮转角剧烈抖动的现象,在高速过弯时具有更高的跟踪精度和稳定性(图7)。
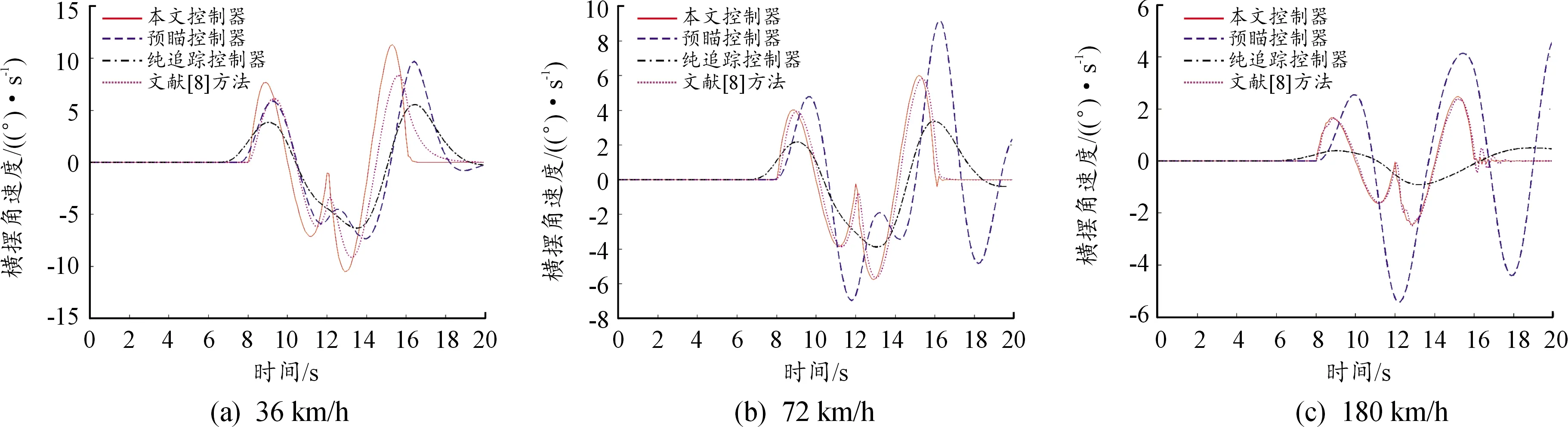
图5 车辆横摆角速度仿真结果
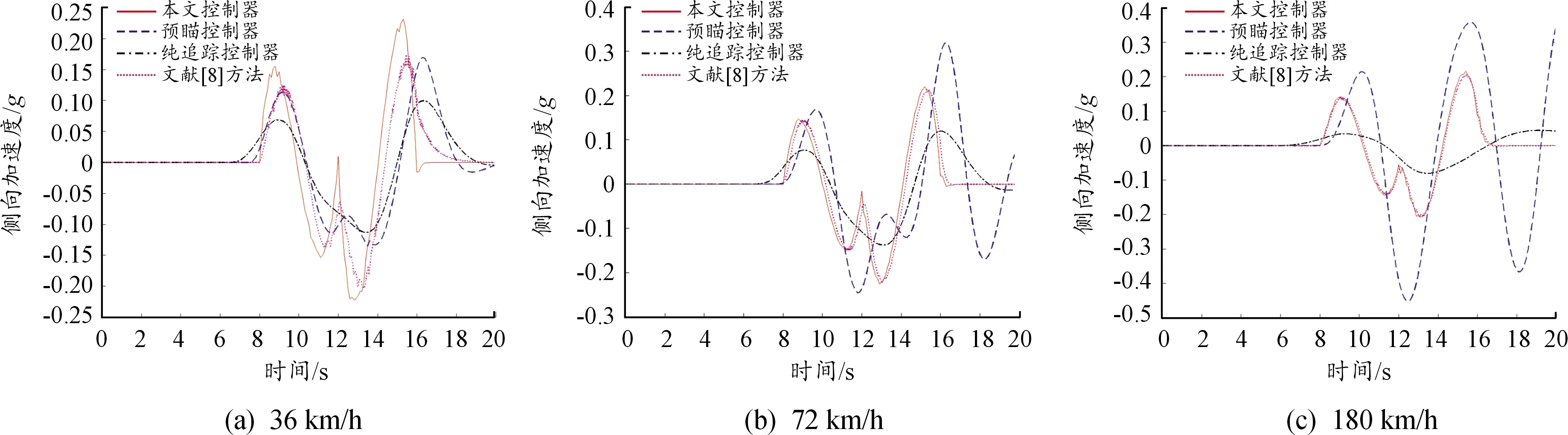
图6 车辆侧向加速度仿真结果
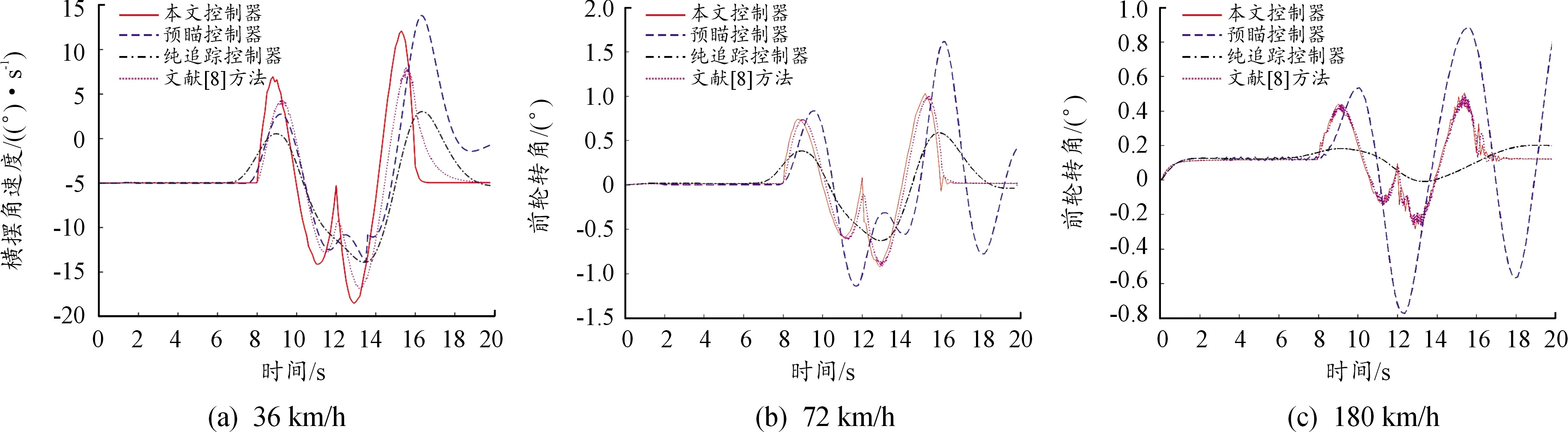
图7 车辆前轮转角仿真结果
3.3 相同车速下不同道路附着系数的路径跟踪实验
为验证复杂路况下路径跟踪效果,进一步对模拟湿滑路面(μ=0.5)和冰雪路面(μ=0.3)进行仿真实验,仿真结果如图8、9所示,干燥路面结果参见上节。
由图8可见,各控制器的跟踪性能随路面附着系数的降低而下降,其中预瞄控制器冰雪路面时的最大横向误差为0.871 m,跟踪能力不足;纯追踪控制器虽没有发生失稳现象,在冰雪路面下后期产生0.402 m的跟踪横向误差;文献[8]方法对弯道响应较差、易积累横向行驶偏差,致使车辆在弯道结束后无法回到路径中心线,产生跟踪偏差;而本文方法的横向误差最大仅有0.041 m,对于实际情况来说可以忽略,仍具有精确的跟踪能力。图9表明车辆以180 km/h行驶时,本文方法在湿滑路面时最大横向误差仅为0.07 m,冰雪路面时最大横向误差为0.36 m,仍具有较好的跟踪能力,车辆各项稳定性参数都在安全范围内。
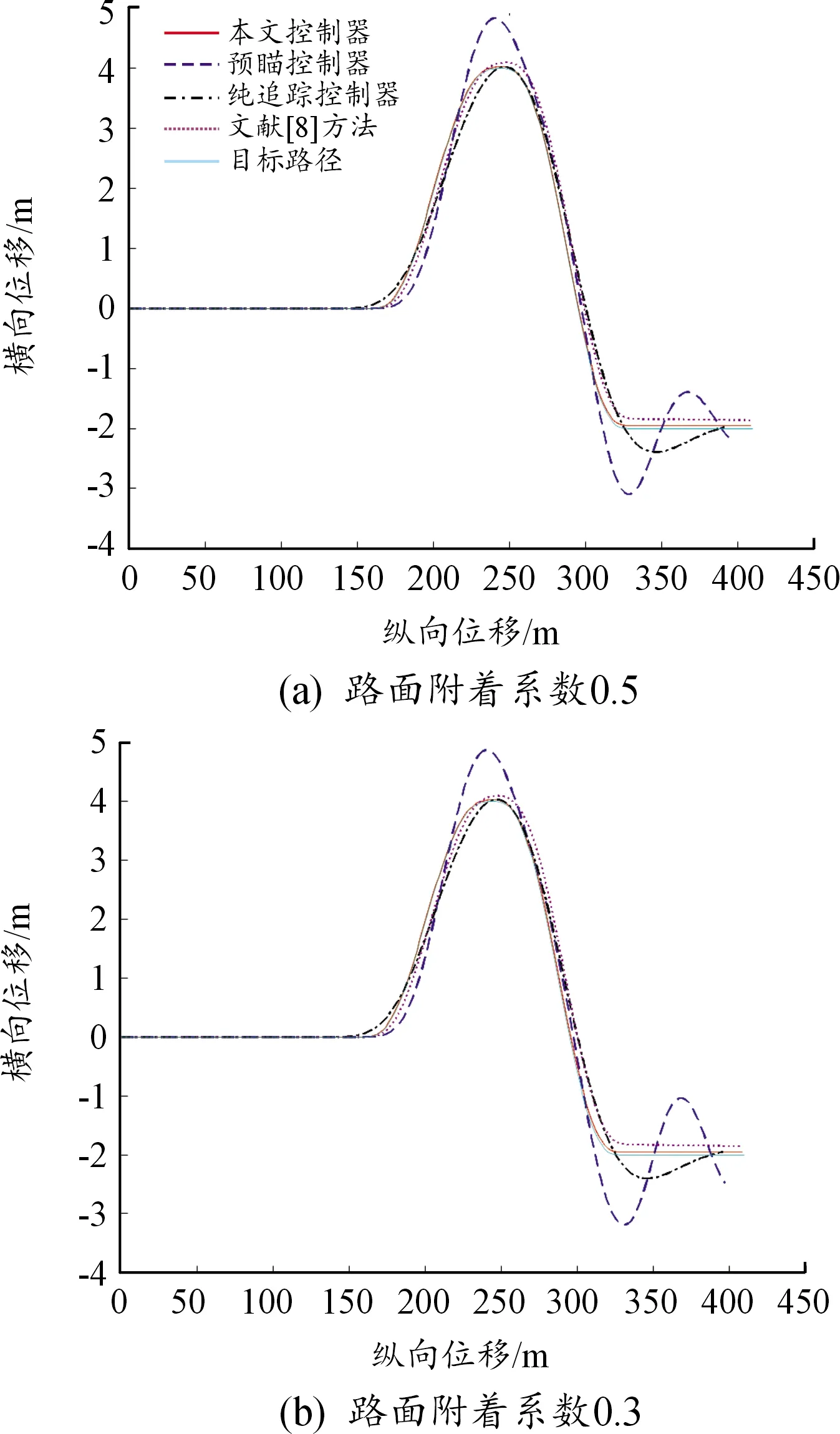
图8 72 km/h路径跟踪效果
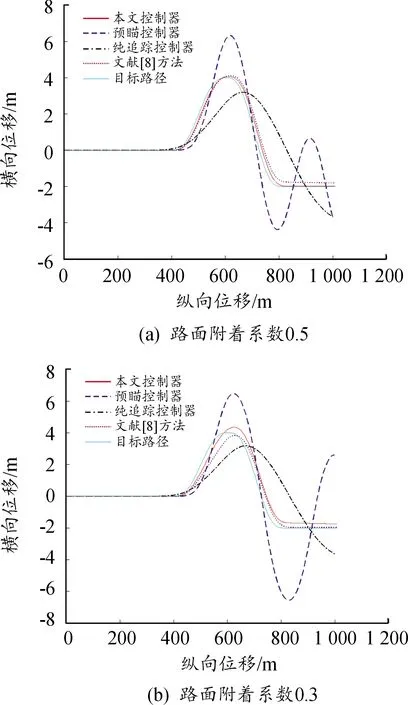
图9 180 km/h路径跟踪效果
4 结论
针对无人驾驶车辆路径跟踪控制器难以满足复杂路况下全速域行驶的问题,提出一种无人驾驶车辆路径跟踪复合控制策略,在保证跟踪精度的前提下,同时能够满足车辆的操纵稳定性和乘坐舒适性要求。主要工作如下:
1) 建立车辆误差状态预测模型,运用MPC控制实现车辆的路径跟踪控制;考虑车速和道路附着系数对跟踪效果的影响,为解决宽速度变化范围及复杂路况下的跟踪精度问题,基于车辆行驶误差信息和道路曲率,运用模糊控制原理设计转角补偿控制器。
2) 建立Simulink和Carsim联合仿真模型,与预瞄控制器、纯追踪控制器和文献[8]方法进行了对比仿真实验,结果表明:本文方法在全路面附着系数及全速域下具有最好的路径跟踪效果,且车辆的动力学参数都处在安全的范围内。虽在极限条件下(高速低路面附着系数)跟踪精度有所下降,但结合转角补偿控制后可有效降低车辆的不安全行为,提高了复合控制策略的鲁棒性。
