绍兴重塑非饱和黏土三轴剪切特性试验研究
2022-03-22吴瑞潜林群仙项祺辰
吴瑞潜 杨 光 林群仙 项祺辰
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000;2.浙江工业职业技术学院 建筑工程学院,浙江 绍兴 312000)
非饱和土在地球表面的分布十分广泛,地下水以上的土体通常处于非饱和状态.随着气候与降雨量的变化,土中吸力会随之改变,非饱和土强度问题也会逐渐突显出来.迄今为止,非饱和土为四相体系(固体、水、空气、收缩膜)这一理论被更多的学者所认可.非饱和土中孔隙气压力与孔隙水压力的差值即为基质吸力.由于历史环境原因,绍兴地区软黏土成因与性质区别于杭州萧山与宁波软黏土,绍兴地区存在大量的第四纪泄湖相、溺谷相与滨海相等海相沉积软黏土层.该软黏土层常年平均水位埋深为0.5~1.0 m,且软黏土沉积厚度大,成层稳定,上部存在大量非饱和土.由于非饱和土中基质吸力的存在使其土性相较于饱和土更加的复杂多变,对工程建设产生重大影响,因此,对非饱和土的研究无论是从理论方面还是工程应用方面都具有非常重要的意义.
在学术界与工程界,针对非饱和土抗剪强度与变形特性问题研究较多.Hogentogler和Barber[1]描述了非饱和土中毛细水的流动状态并且证明了毛细水的流动符合表面张力、重力和水力学的原理.A W Bishop[2]对Terzaghi饱和有效应力公式进行拓展,引入参数χ提出单变量抗剪强度理论公式;D G Fredlund[3-4]经过大量试验总结得出用应力状态变量描述非饱和土强度特性与非饱和土四相体系更加符合,提出了双变量抗剪强度理论.尹俊等[5]通过改进的普通三轴试验让不同含水率的重塑土样恢复原始应力研究非饱和土的应力-应变关系,在双曲线模型基础上总结出含水率引入硬化参数中的非饱和土本构模型.王斯海等[6]针对宁波地区筑堤黏土运用土水特征曲线与非饱和土直剪试验相结合的方法分析了含水率、颗粒级配及基质吸力对非饱和土抗剪强度的影响,研究结果表明:非饱和土抗剪强度很大程度上取决于土体内基质吸力转化为有效黏聚力的转化情况及基质吸力和吸应力之间的转化关系.戚国庆等[7]等利用某滑坡体的原状样与重塑样研究基质吸力变化与体积应变之间的关系,研究结果表明:试样的体积应变随着基质吸力的增大以对数函数形式线性增大,并且体积模量服从幂函数关系.基质吸力在非饱和土中对其强度的影响机理认识尚未完全成熟,以不同类型非饱和土为研究对象,探讨其强度参数的影响规律,一直是国内外非饱和土的研究热点之一.
本文以浙江绍兴某基坑黏土为研究对象,用非饱和土三轴仪对重塑样进行控制基质吸力与净围压的三轴固结排水剪切试验,研究绍兴地区非饱和重塑黏土强度、变形特性,为实际工程应用提供参考.
1 非饱和土抗剪强度理论
由于基质吸力的存在,土中的有效应力不再等于粒间压力,因此饱和土的抗剪强度理论公式不适用于非饱和土.经过国内外学者的不断试验与总结,经典非饱和土抗剪强度公式主要是A W Bishop等提出的单变量抗剪强度公式与D G Fredlund等提出的双变量抗剪强度公式,在此基础上还有学者提出了一些经验公式.其中由于Bishop单变量抗剪强度公式参数χ取值的影响因素众多,不容易确定且有效应力与基质吸力对土体抗剪强度作用机理不同,简单的叠加是不合理的,这使其在实际工程中的应用受到了限制.因此在理论与实际工程中应用较为广泛的是Fredlund双变量抗剪强度公式[8],如下:
τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb
(1)
式(1)中:c′与φ′均是饱和黏性土的抗剪强度指标,(σ-ua)是净法向应力,(ua-uw)为基质吸力,φb表示抗剪强度随基质吸力而增加的速率.
将常规三轴Mohr-Coulomb强度破坏包络进行延伸,以剪应力τ为纵坐标、(σ-ua)和(ua-uw)为横坐标,可以绘制出三维非饱和土强度破坏包络面,在空间上,平面可能会有一些弯曲.如图1所示.三维坐标的前缘面表示饱和土状态.从图中可以看出,净法向应力与基质吸力对非饱和土的力学特性影响是不同的,有效摩擦角φ′表示抗剪强度随净法向应力变化情况,φb表示抗剪强度随基质吸力变化情况.除了以上两种经典非饱和土抗剪强度理论公式,还有一些学者总结得到的非饱和土经验公式,如Vanapalli等[9]经过大量试验总结得出了采用土水特征曲线(SWCC)来预测非饱和土抗剪强度的公式;沈珠江等[10]发现可以采用双曲线模型来拟合重塑非饱和黏土抗剪强度公式等.
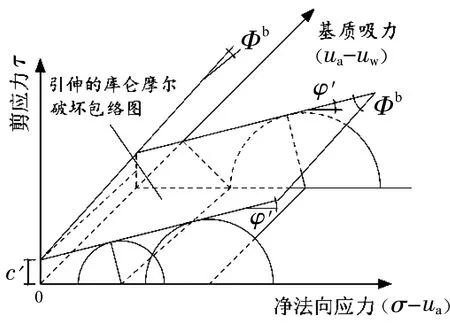
图1 非饱和土的Mohr-Coulomb破坏包络面
2 试验概况
2.1 试验土样
试验全部用土取自浙江绍兴某基坑,取土深度为3.5~4.0 m,为第三系上更新统上段黏性土,冲湖积成因,土体呈棕黄-灰黄色,具少量铁锰质浸染与钙质结核.在室内对原土进行烘干、碾碎,过2 mm筛,根据试验所需含水率配制土样放置保湿缸内静置24 h后备用.试样为标准三轴土样,高80 mm,直径39.1 mm,试样的基本物理性质指标如表1所示.

表1 试样的基本物理性质
2.2 试验方案
共3组9个土样进行控制吸力的三轴固结排水试验,研究在不同吸力作用下土的强度与变形特性.试验中基质吸力s分别控制为50 kPa、100 kPa、200 kPa,净围压(σ3-ua)分别为30 kPa、130 kPa、230 kPa.控制土样初始含水率w=21.0%,干密度ρd=1.6 g·cm-3.详细试验方案如表2所示.
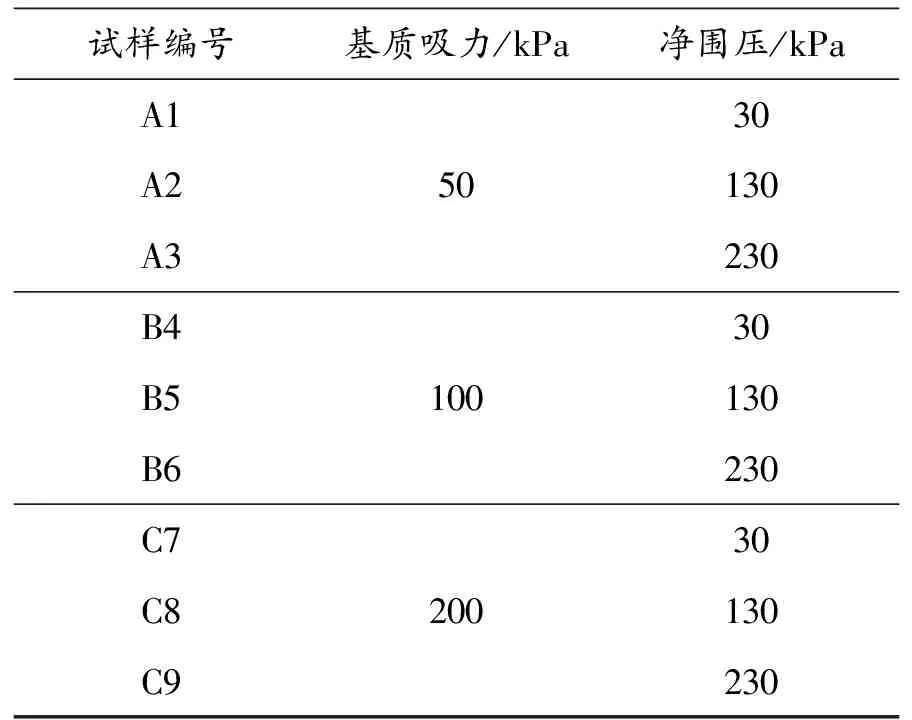
表2 试验方案
2.3 试验过程
①在试验开始之前要先制备“无气”实验用水,将试验仪器的控制器与管路内气体排净并且需饱和陶土板24 h以上;②按照《土工试验方法标准》(GB/T 50123—2019),试验前将试样放入真空饱和装置内饱和24 h,确保试样完全饱和;③取出预饱和试样称其重量,在试样一端放透水石与滤纸,另一端无透水石、滤纸置于陶土板上,用橡胶膜固定试样;④安装内外压力室罩,将轴向压力传感仪紧置于试样帽上;⑤注水排气,检查有无漏气或漏水现象,打开、关闭相应阀门即可进行试验.
试验采用轴平移技术,试样在仪器设定的孔隙气压与围压下至固结稳定,固结稳定的判定标准为2 h内体变和排水均不超过0.01 cm3,且最少历时40 h.待试样固结稳定后即可剪切,剪切速率为0.003 2 mm/min;剪切至轴向应变达15%后停止剪切.
2.4 试验仪器
本试验所用的仪器为南京泰克奥公司生产的TKA新型双压力室非饱和三轴仪,内外压力室壁均由高强度的有机玻璃材质构成,玻璃能够彻底根除水的吸附作用,有效控制试验误差.控制方式与数据采集全部由电脑自动控制,其主要组成部分有双腔压力室、控制系统、测量与采集系统以及数据处理四个部分.具体构成如图2所示.

图2 TKA双压力非饱和土三轴仪
3 试验结果分析
在非饱和土中运用净总应力(σ-ua)和基质吸力(ua-uw)两个独立的应力状态变量来衡量强度特性,并且通过指定不同的参数反映状态变量对土样抗剪强度的影响,大量的试验表明这种方式具有很好的可行性.因此本文采用以下公式及符号来描述应力状态[11]:
(2)
q=σ1-σ3
(3)
s=ua-uw
(4)
式中:p为净平均应力,q为偏应力,s为基质吸力,ua为孔隙气压力,uw为孔隙气压力.
3.1 应力-应变关系曲线
在相同基质吸力,不同净围压下三轴剪切试验的应力-应变曲线如图3所示.从中可以发现,应力-应变关系曲线近似双曲线函数,与1963年Kondner[12]根据大量室内三轴试验得出的结论一致.该土样的应力-应变曲线主要表现为硬化型,没有明显的破坏点.在同一基质吸力下,随着净围压的增大,非饱和黏性土的抗剪强度逐渐增大,且前期偏应力上升较快,当轴向应变至3%后,曲线斜率明显减小.尤其是在净围压为30 kPa时,前期应力快速增加,后期应力增大曲线斜率近似为0,表明在低围压状态下,土样强度主要由前期强度提供.在较高吸力的作用下,土的硬化特征更加明显.在相同的净围压下,随着基质吸力的增加,土的抗剪强度性质也有明显增强.其主要原因是基质吸力的增强,减少了土体孔隙中的水分,使土颗粒间缺少了水的润滑作用,同时气—水界面的收缩膜随着基质吸力的改变对土体的抗剪强度也起到了很大作用.
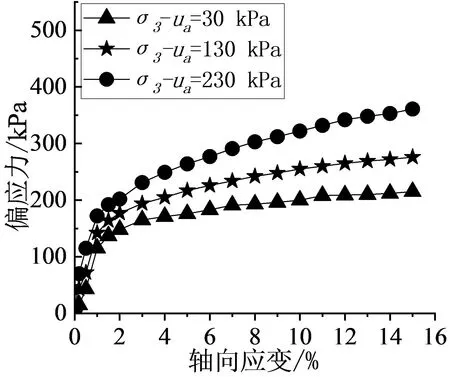
(a)s=50 kPa
根据既有研究成果,本试验土样的应变硬化特性与非饱和红土[13]在较高围压条件下表现出明显的硬化特性,而在低围压下表现不明显相似,但与非饱和黄土[14]剪切破坏特性具有明显的差异.非饱和黄土破坏形式分别为:硬化型、理想弹塑性和软化型,并且绍兴非饱和黏土由于历史成因与环境因素,其与杭州萧山[15]、宁波非饱和黏土区别是其轴向应变3%之前偏应力增大较快,后期增幅逐渐减小.因此在工程设计中可充分利用非饱和黏土前期偏应力增大较快,后期残余强度较大特性,提高工程效益与安全性.
3.2 基质吸力与抗剪强度参数关系
本试验中的9个土样均呈应变硬化型特征,无明显的破坏点,因此选取轴向应变15%所对应的轴向应力作为破坏应力(qf,pf).具体破坏应力值如表3所示.根据表3中数值在p-q平面内画出强度包线如图4所示,从图中可以发现,基质吸力相同的p-q值点均在一条直线上,因此可用陈正汉提出的有关非饱和土强度参数算法[16]进行参数计算.运用如下函数关系式对图中直线进行拟合:
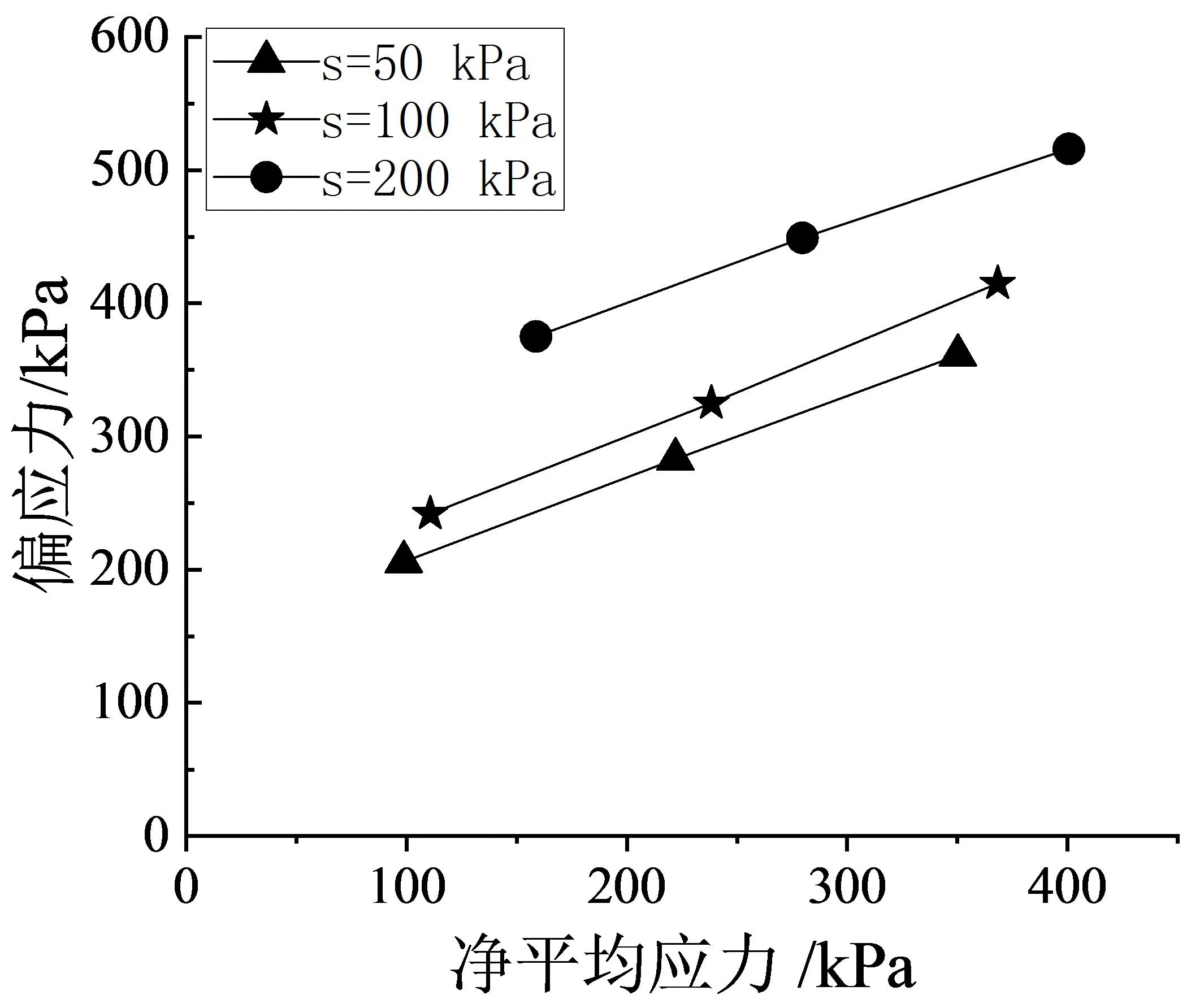
图4 偏应力-净平均应力平面强度包线
qf=ξ+pftanω
(5)
式(5)中:ξ和tanω分别为直线的截距和斜率.
土的有效内摩擦角φ′由下式求得:
(6)
土的总黏聚力c由下式求得:
(7)
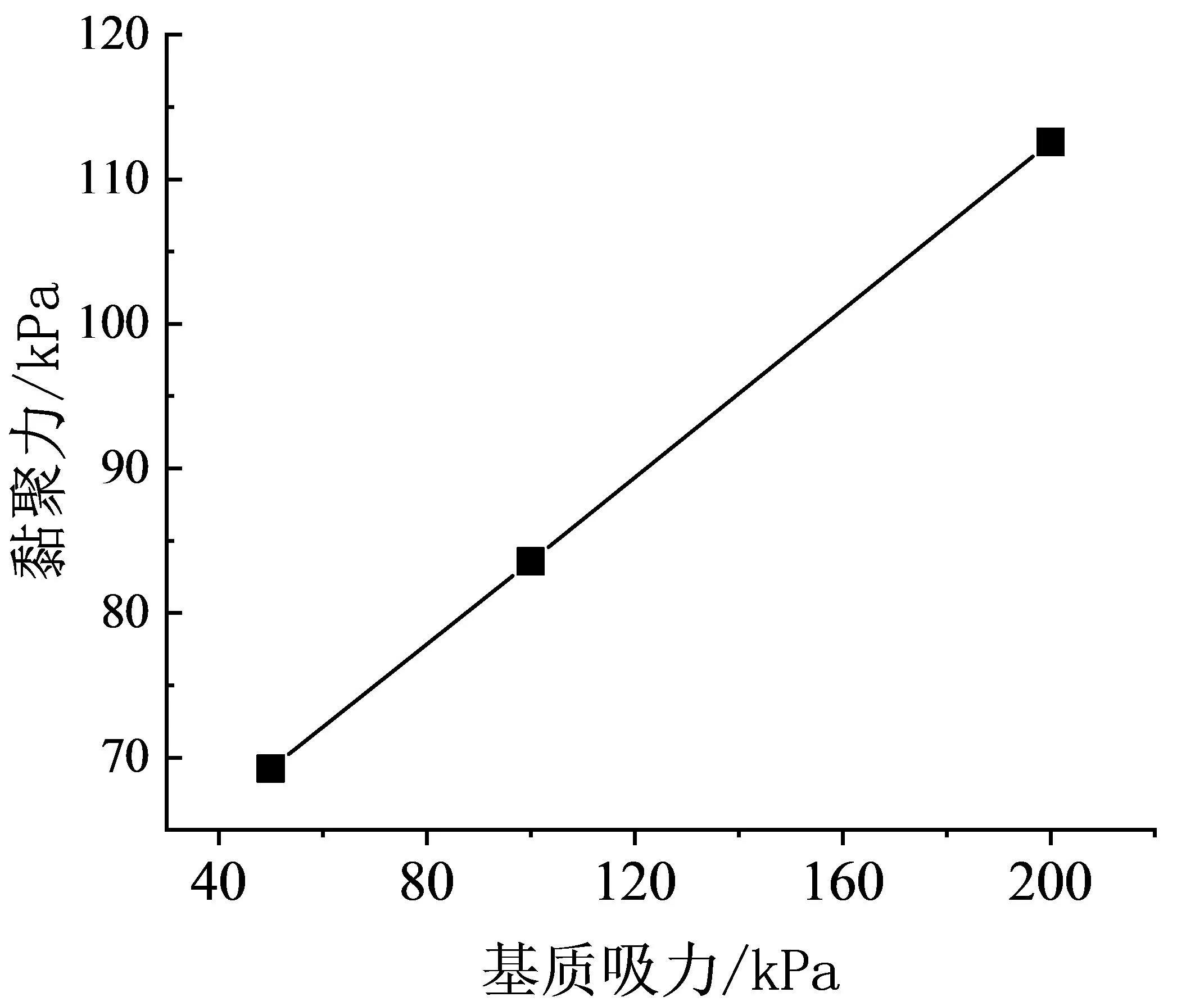
从表3中可以看出,随着基质吸力的增大,重塑非饱和黏土的黏聚力c与有效内摩擦角φ′都有不同程度的增大,黏聚力的增大更为明显,这也充分说明了基质吸力在增强土样的抗剪强度机理上主要是黏聚力起主导作用,特别是在高吸力的作用下其影响更加突出,究其原因是土体孔隙的毛细作用使表面张力增加,引起土颗粒的气封增加.根据表3中的值可绘制出黏聚力c、有效内摩擦角φ′与基质吸力的关系曲线,如图5所示.
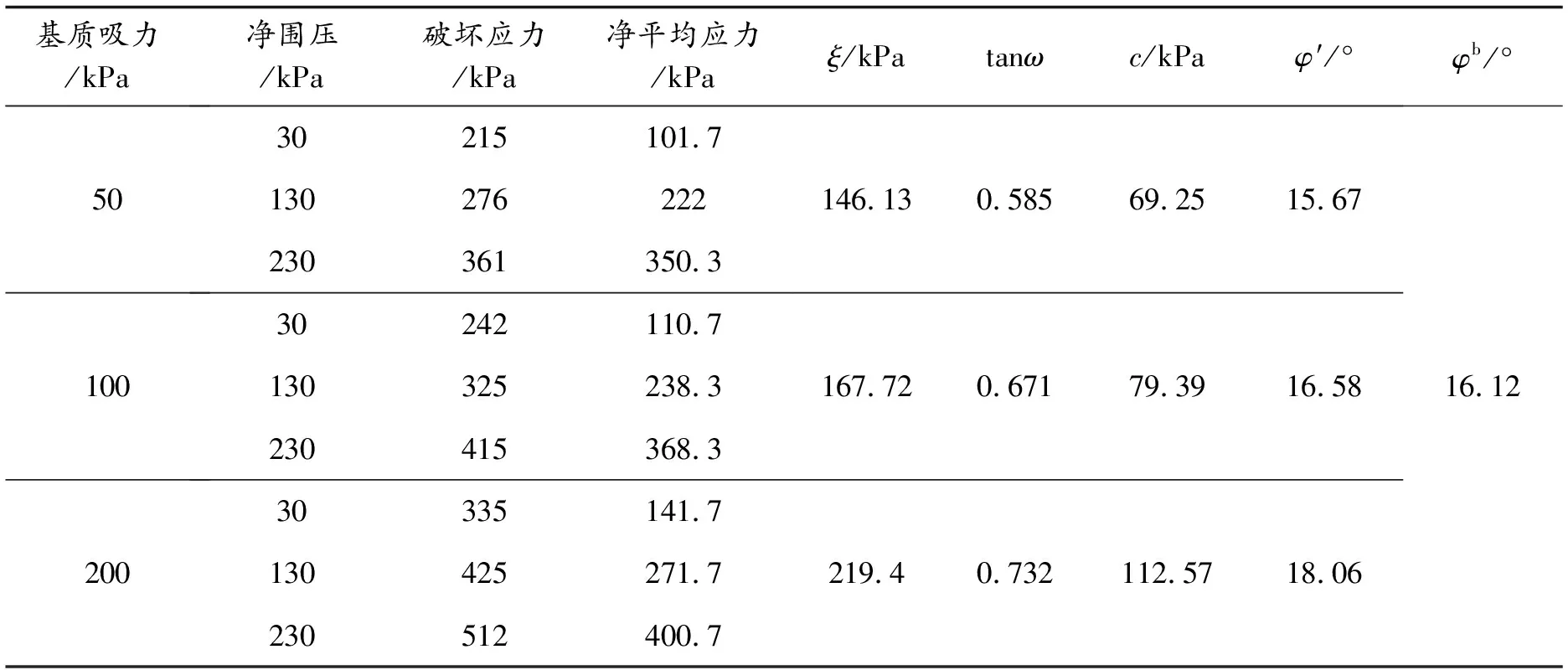
表3 土样的强度参数
(a)黏聚力与基质吸力关系曲线
由于本试验分析采用2个应力状态变量,因此运用Fredlund等提出的双变量非饱和土抗剪强度公式即式(1)来描述土体的强度,从图中可以看出:c-s近似线性关系,随着基质吸力的增大,土的有效黏聚力c也随之增大,其在单位基质吸力上的增幅就是tanφb,φb即为c-s拟合直线的倾角,由此便可计算出本试验土样φb=16.12°.
3.3 体积应变-轴向应变关系
本试验采用的是双压力室非饱和三轴仪,由于内外压力室壁都是高强度有机玻璃材质,同时内外围压均为σ3,内压力室不会产生变形,因此本试验认定内压力室的水体积变化就是试样体积的变化,通过体变仪就能够自动连续的记录试样体积变化.
土样在剪切过程中体积变化(εv)与轴向应变(εa)的关系曲线如图6所示.从图中可以看出,在不同的基质吸力与净围压下,体变呈剪胀趋势,不存在剪缩现象.从数值上可以看出,基质吸力为50 kPa、100 kPa时,体积应变随净围压的增幅大致相同,其分别增加0.57%、0.51%、0.7%、0.7%.基质吸力为200 kPa时,其随每级净围压的增幅分别为0.59%、1.35%.由于基质吸力的增大,土体中孔隙气体积增大,在剪切过程中更多的孔隙气被压缩,且净围压增大,土中孔隙半径减小.因此基质吸力越大,净围压越大,体积应变随轴向应变增大,在轴向应变达至3%之前体积应变增幅较大,之后增幅逐渐减小.这与前面分析的应力-应变关系相对应,表明偏应力的增幅与体积应变的增幅成正比关系.根据既有研究成果,合肥地区[17]非饱和黏土体积随轴向应变先剪缩后剪胀,并且与净围压有关,净围压越小,形成的反差越大.而非饱和黄土随着基质吸力的增大剪胀特性越明显,表明不同区域的非饱和黏土受到基质吸力与净围压的影响而产生的现象是不同的,并且土体体积的变化对实际工程有重大的影响,因此研究绍兴地区非饱和黏土基质吸力对体积应变的影响具有一定的工程意义.
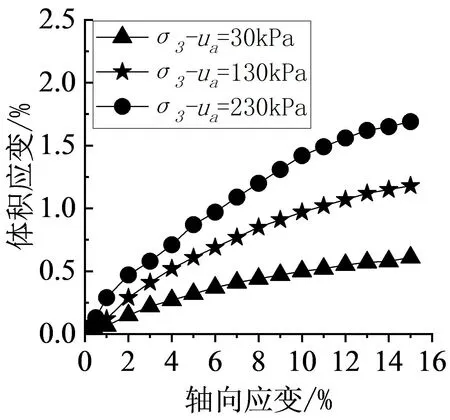
(a)s=50 kPa
将基质吸力、净围压相同的试样破坏后的体积应变取平均值,分别绘成如图7、图8所示的体积应变与基质吸力的关系曲线、体积应变与净围压的关系曲线.从图中可以看出,基质吸力改变引起的体积应变小于由净围压改变引起的体积应变,且基质吸力引起的体应变的变化斜率逐渐减小,净围压引起的体应变斜率逐渐增大,这与沈珠江[18]提出的“基质吸力只有一部分能有效增加土体的强度与抗变形能力”广义吸力概念相符.因此在重塑非饱和黏土中,对体积应变影响更大的是作用于土骨架上的“净法向应力”[19-20].
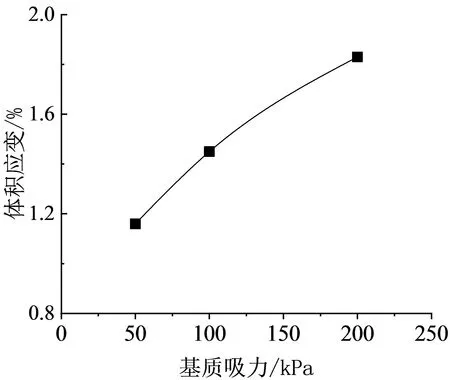
图7 体积应变-基质吸力关系曲线
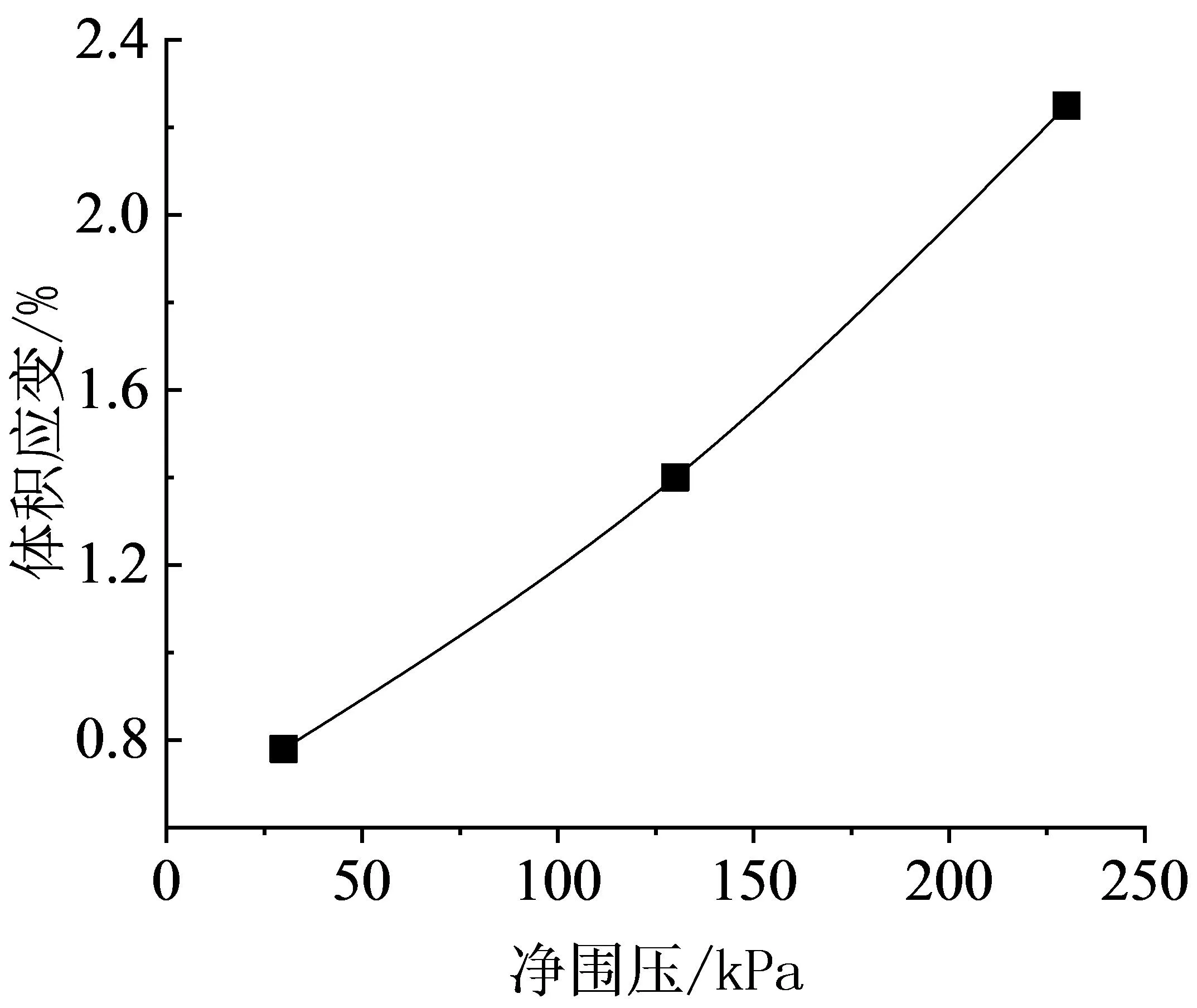
图8 体积应变-净围压关系曲线
4 结论
以绍兴重塑非饱和黏土为研究对象,采用双压力室全自动非饱和土三轴仪,进行控制基质吸力与净围压的三轴固结排水剪切试验,主要得出以下结论:
(1)基质吸力与净围压为常数时,试样的应力-应变曲线近似双曲线函数,主要表现为应变硬化型,基质吸力越大,净围压越大,土样硬化特征越明显,抗剪强度越大.绍兴重塑非饱和黏土与杭州萧山、宁波非饱和黏性土区别是其轴向应变3%之前偏应力增大较快,后期增幅逐渐减小.
(2)随着基质吸力的增大,试样的黏聚力c值与有效内摩擦角φ′值都有不同程度的增大,前者对基质吸力的改变更加敏感.此外,根据双变量抗剪强度理论得出与基质吸力相关的内摩擦角φb=16.12°.
(3)随着净围压与基质吸力的增大,试样体积应变都有不同程度的增幅,且基质吸力引起的体积应变小于由净围压引起的体积应变,说明在重塑非饱和黏土中,对体积应变影响更大的是作用于土骨架上的“净法向应力”.与合肥地区重塑非饱和黏土先剪缩后剪胀特性不同的是绍兴地区非饱和黏土在三轴剪切过程中体变呈剪胀趋势,无剪缩现象.
研究了解绍兴重塑非饱和黏土三轴剪切特性,尤其是其硬化特性以及体积应变规律,有助于我们正确认识土体特性,并为绍兴地区地基处理、基坑工程等设计施工土体参数选择提供借鉴.
