地铁隧道施工引起地层变形的模型试验研究

王天佐 陈 雷 薛 飞 王林翔 SANA Moctar

(1.绍兴文理学院 土木工程学院，浙江 绍兴 312000；2.浙江省岩石力学与地质灾害重点实验室，浙江 绍兴 312000；3.浙江省山体地质灾害防治协同创新中心，浙江 绍兴 312000)

0 引言

近年来，随着城市的经济发展，地面交通愈加拥堵，许多城市开始发展地下空间，修建地铁隧道.地铁隧道施工会对土体产生扰动从而引起地层变形，对上层建筑物以及各种埋设管线产生巨大影响，甚至导致地面塌陷、建筑物开裂、管线破裂等灾害[1].地铁施工中引起的地层变形是各种因素综合作用的结果，众多因素之间又相互影响相互作用，使得原本复杂的地层变形问题更加难以考虑.而从根源上讲，地铁隧道施工产生的地层损失是导致地层变形的根本原因[2-3].从地层损失的角度出发可抓住沉降问题的本源，使复杂的隧道施工引起的地层变形问题在一定简化的基础上得以解决，具有理论和现实意义.

国内外针对地层损失对地层沉降影响规律的研究中，物理模型试验法是最有效且直观的方法之一.Mair等[4]针对浅埋隧道进行了离心模型试验，研究浅埋粘土地层中隧道施工产生的地层损失对地表沉降的影响.Idinger等[5]通过小型隧道模型的离心试验，研究了不同覆盖压力下隧道工作面的塌陷破坏机理及地表沉降规律.何川等[6]基于自主研制的土压平衡式模型盾构机开展室内掘进实验，研究了黄土地层条件中盾构掘进对地层扰动情况及盾构施工关键参数的匹配问题，并总结了地表沉降曲线的特征参数.王忠昶等[7]通过建立双洞隧道模型，研究左右隧道错开施工导致的变形问题，发现随着地层深度的增加，地层沉降曲线的非对称双峰特征越明显，并从水平变形的角度提出了研究区域的工程建议.王正兴等[8]通过室内模型试验研究了砂土中沉降槽宽度系数与深度及最大沉降量之间的关系，并提出了地层体积传递率的概念.王非等[9]通过自制模型试验箱研究了砂性土中隧道施工引起的地层沉降模式，发现沉降槽宽度系数只与沉降槽所处深度密切相关而与沉降槽中心最大沉降无关.Fang Y等[10-11]进行了大型室内盾构模拟试验，探究盾构施工过程中不同开挖参数所引起的地表沉降特性，得到了盾构开挖前、开挖中、开挖后地层的变形演变规律.梁庆国等[12]通过石膏模拟隧道衬砌，并在观监测点布置土压力盒、应变片、百分表等，研究了隧道施工过程中衬砌的应力及变形特性.黄赵美等[13]通过自制砂箱模型试验研究了盾构超挖过程中埋深及土体损失率对地表沉降变化规律的影响.大多学者针对不同性质的土层中地表的沉降规律进行研究，而对土层内部的变形及传递过程研究较少.

本研究通过自制模型试验箱，利用排液法改变隧道体积来直接控制地层损失率，探究不同地层损失率下地表及地层内部的变形过程，以揭示地层直接损失对地层环境的影响规律.

1 室内模型试验介绍

1.1 模型试验箱与隧道模型

研究所用的模型试验箱为自主研发并已申请专利，宽度方向尺寸可调，可用于模拟平面应变问题或三向应变问题，本次研究主要针对平面应变问题.实际模拟对象中盾构隧道直径为6 m，取相似系数40，则隧道模型直径15 cm，模型箱长度至少大于3倍硐径范围，取为150 cm.模型高度为70 cm，宽度无须过大，设置为30 cm，即模型箱尺寸为150 cm×100 cm×30 cm，如图1所示.

图1 物理模型试验箱

隧道模型由PVC材料自制而成，模型外部贴合一层乳胶膜，并用聚氨酯胶密封.乳胶膜与PVC管间通过细管注排水，基于卡默尔KKDD24B-17A型蠕动泵控制液体体积排出量，如图2所示.

图2 隧道模型

乳胶膜内水的排出体积，即为地层的直接损失量，地层损失率如公式(1)所示，此即为排液法.

(1)

式中Vl为地层损失率，V为单位长度地层损失量，2r0为隧道外径.

1.2 土层铺设

试验以烘干的石英砂作为填筑材料，通过筛分法确定石英砂颗粒直径主要分布在0.3～1 mm之间，d50为0.6 mm.通过直剪试验测得石英砂内摩擦角为32 °，粘聚力为0.本次试验考虑到地层均匀性，用简化砂雨法进行填筑，即在固定高度石英砂通过筛网自由下落，下落高度为80 cm.石英砂密度经过测试为1.53 g/cm3，实际隧道埋深约为10～20 m，试验中隧道埋深取1.5d，即22.5 cm，隧道下部土层厚度为35 cm.

1.3 位移传感器布置

本次试验主要测量地表及地层内部的竖向位移变化，所用位移传感器为北京泽佰斯特科技有限公司定做的全桥位移计，共17支，精度0.01 mm，探头长度分别为30 cm、35 cm、40 cm，分别用来监测地表及地层内部不同深度处的竖向位移，如图3所示.位移计端部粘贴小铁片，增大与土层的接触面积以提高精度.另外，采用信恒电子科技有限公司32通道CM-1L-32型静态电阻应变试仪用于数据实时监测.

图3 模型箱内位移监测点布置

测量点位的布置分为4层，每层点位间距5 cm，如图4所示.同一层点位之间，中间密两边疏，间距分别为7.5 cm、7.5 cm、11 cm、11 cm，由于变形的对称性及布置空间限制，监测点位中心轴线两侧交错布置，其中实心圆点为位移计监测点位，空心圆点为对称换算点位.

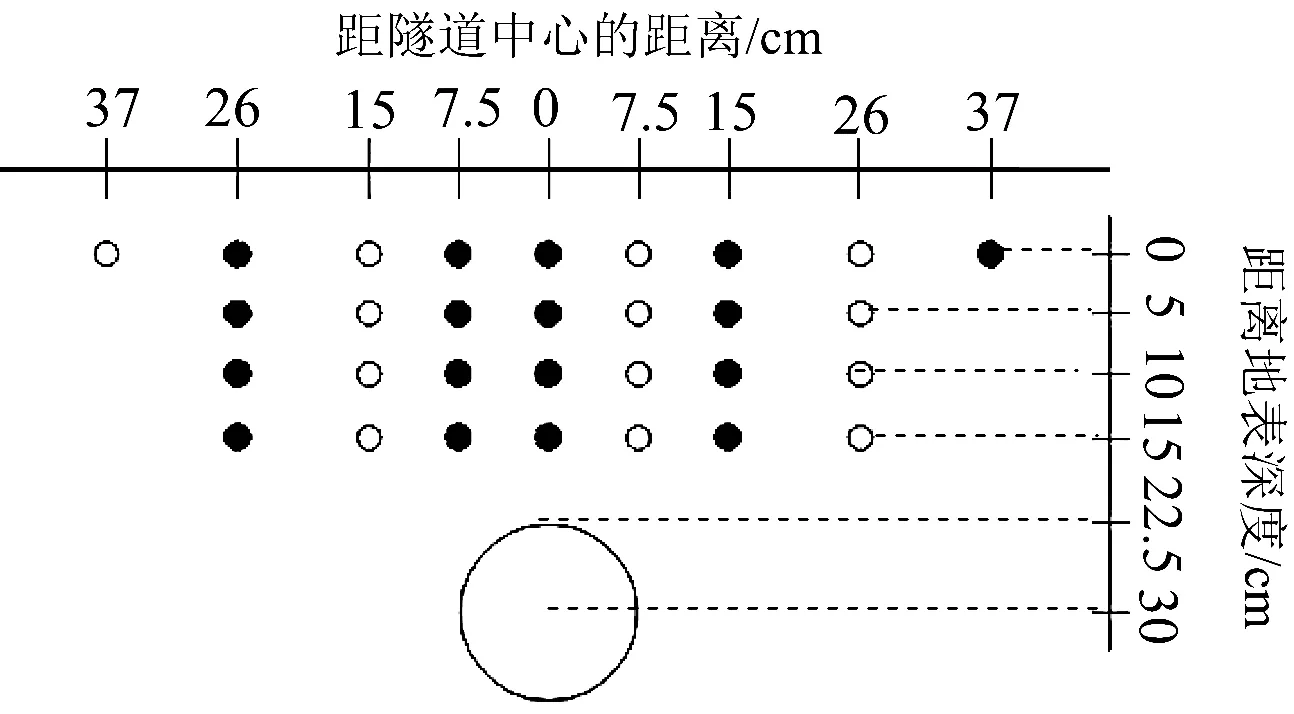
图4 位移计点位布置图

1.4 试验过程

试验开始前，将17支位移计连接32通道静态电阻应变试仪并用电脑进行数据采集调试工作.将隧道模型乳胶膜外细管连接蠕动泵，液体排出速度为300 ml/min.启动蠕动泵后，实时监测不同点位变形数据.模型布置完成如图5所示，模型箱上已标注比例尺以方便观测，柱体上二黑一白段标尺共15 cm.

图5 室内模型试验布置图

2 试验结果分析

通过排液法可以控制地层损失率，分别进行了地层损失率为5%、10%、15%、20%和25%的试验，同步进行地层内部及地表的位移监测.

2.1 地层损失率对地表沉降的影响

不同地层损失率下地表沉降监测结果如图6所示.

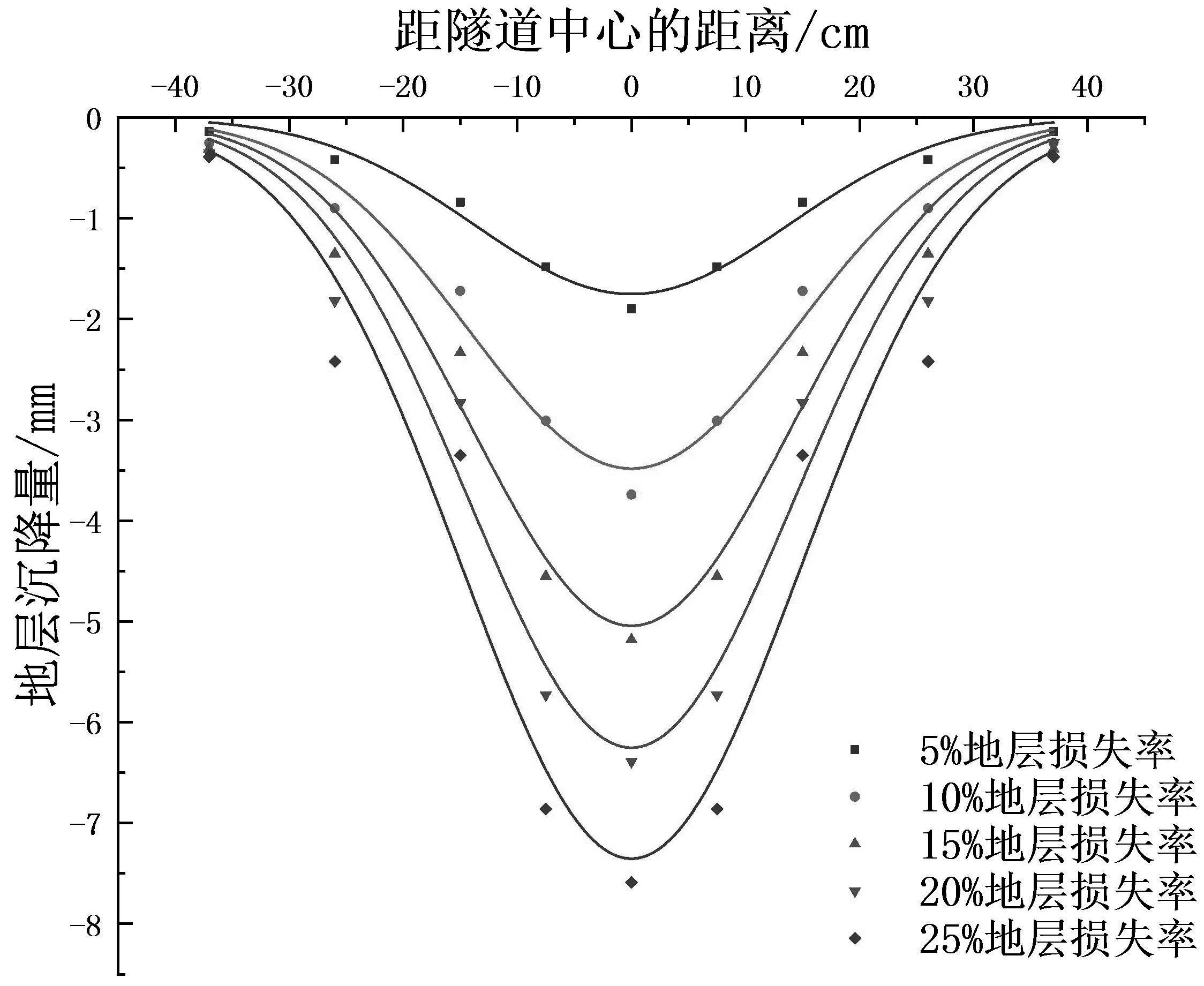
图6 不同地层损失率对地表沉降影响曲线图

将沉降曲线分别用Peck高斯公式进行拟合，如表1所示.

表1 不同地层损失率下地表沉降

从地表沉降曲线可以看出，不同地层损失率下地表变形规律基本一致：隧道中心正上方地表沉降最大，往两侧逐渐减小；随着地层损失的增大，沉降增加，基本符合正态分布，决定系数R2为0.933～0.971，拟合效果较好.

为探明地表沉降的大致范围，对拟合曲线上的特征点进行求算.距离中心22.5 cm(1.5d)的沉降量为-0.46 mm～-2.32 mm，为最大沉降量的26%～32%；距离中心30 cm(2d)的沉降量为-0.16 mm～-0.95 mm，为最大沉降量的6%～13%；距离中心37.5 cm(2.5d)的沉降量为-0.05 mm～-0.33 mm，为最大沉降量的3%～4%.可知，地表沉降量距离隧道横断面中心轴线2.5倍硐径范围外均小于最大沉降量的5%，沉降相对较小可以忽略，故可视隧道上方5倍硐径为地表沉降的影响范围.

为研究地表沉降量与地层损失率之间的关系，做出地层损失率与对应地表最大沉降量之间的关系，如图7所示.当地层损失率为0时，地表最大沉降为0.用二次函数进行拟合得到：

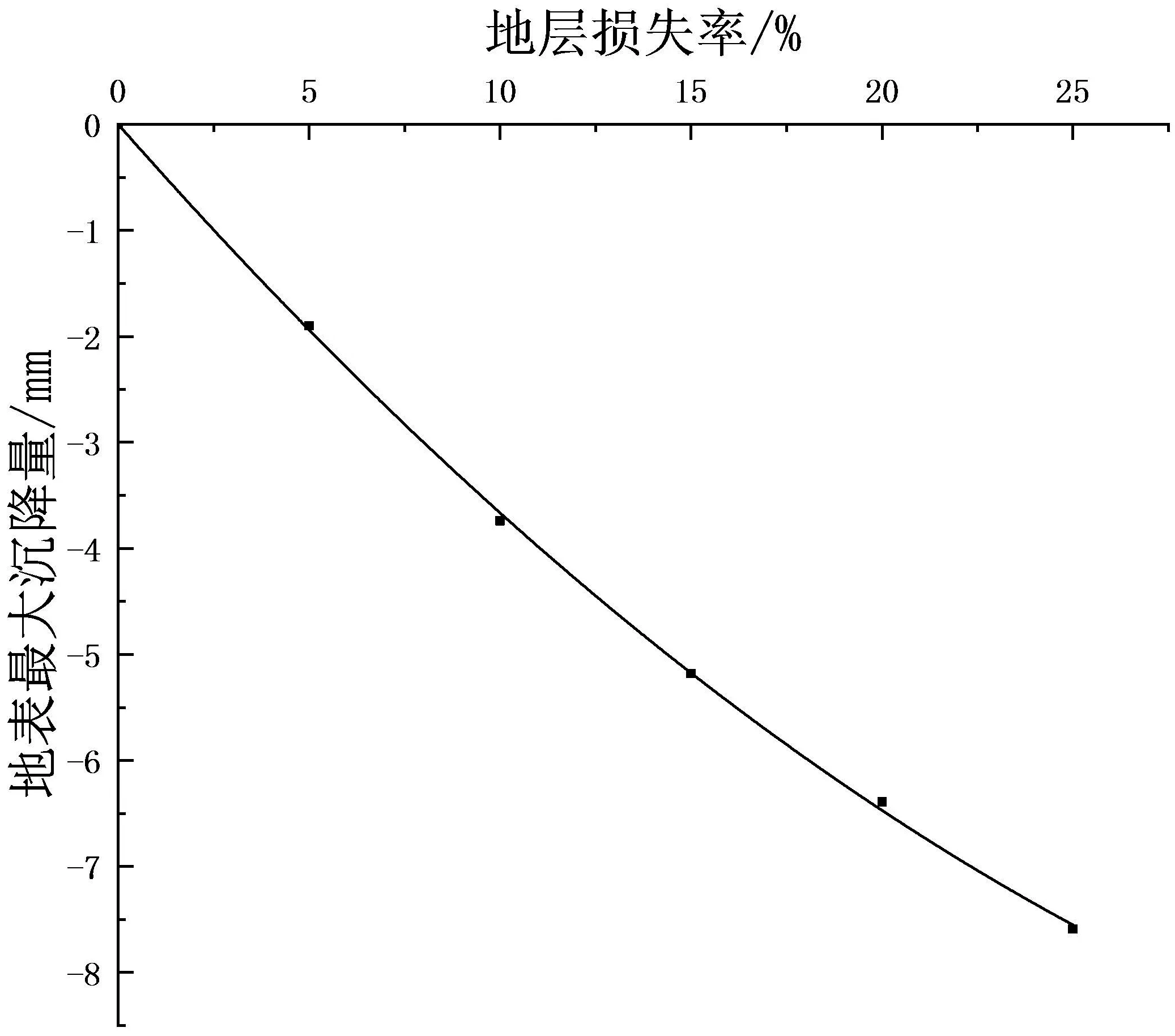
图7 地表最大沉降量与地层损失关系图

y=-0.41x+0.0043x2

(2)

二次函数拟合效果很好，决定系数R2达到1.00.从图7可以看出，地表最大沉降随着地层损失率的增加而增大，且基本呈二次函数关系.可见地层损失对地表最大沉降的影响显著.通过该趋势，可对其他非黏性土中由于地层损失而产生的地表最大沉降进行预测.

将各地层损失率对应的沉降槽宽度系数绘制成曲线得到图8.

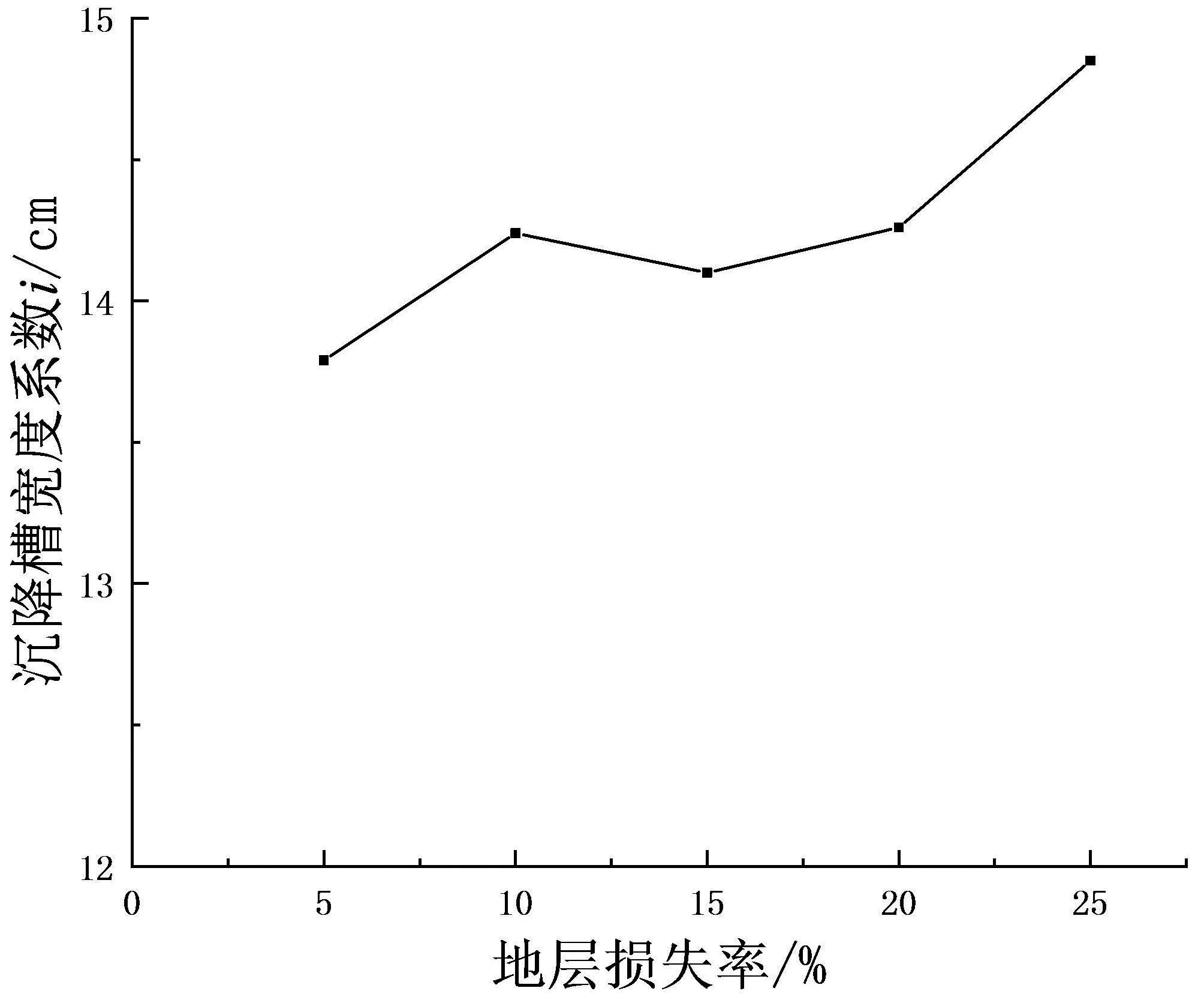
图8 地表沉降槽宽度系数与地层损失率关系图

从图8可以看出，沉降槽宽度系数的范围为13.5～15，约为2倍硐径.基本趋势为随着地层损失率的增加而增大，但增长量较小.说明地层损失率对地表沉降槽宽度的影响不显著.

2.2 不同地层损失率下地层内部变形传递

由不同埋深处的位移计可以得到对应的位移沉降曲线，不同地层损失率对应的沉降曲线如图9—图13所示.

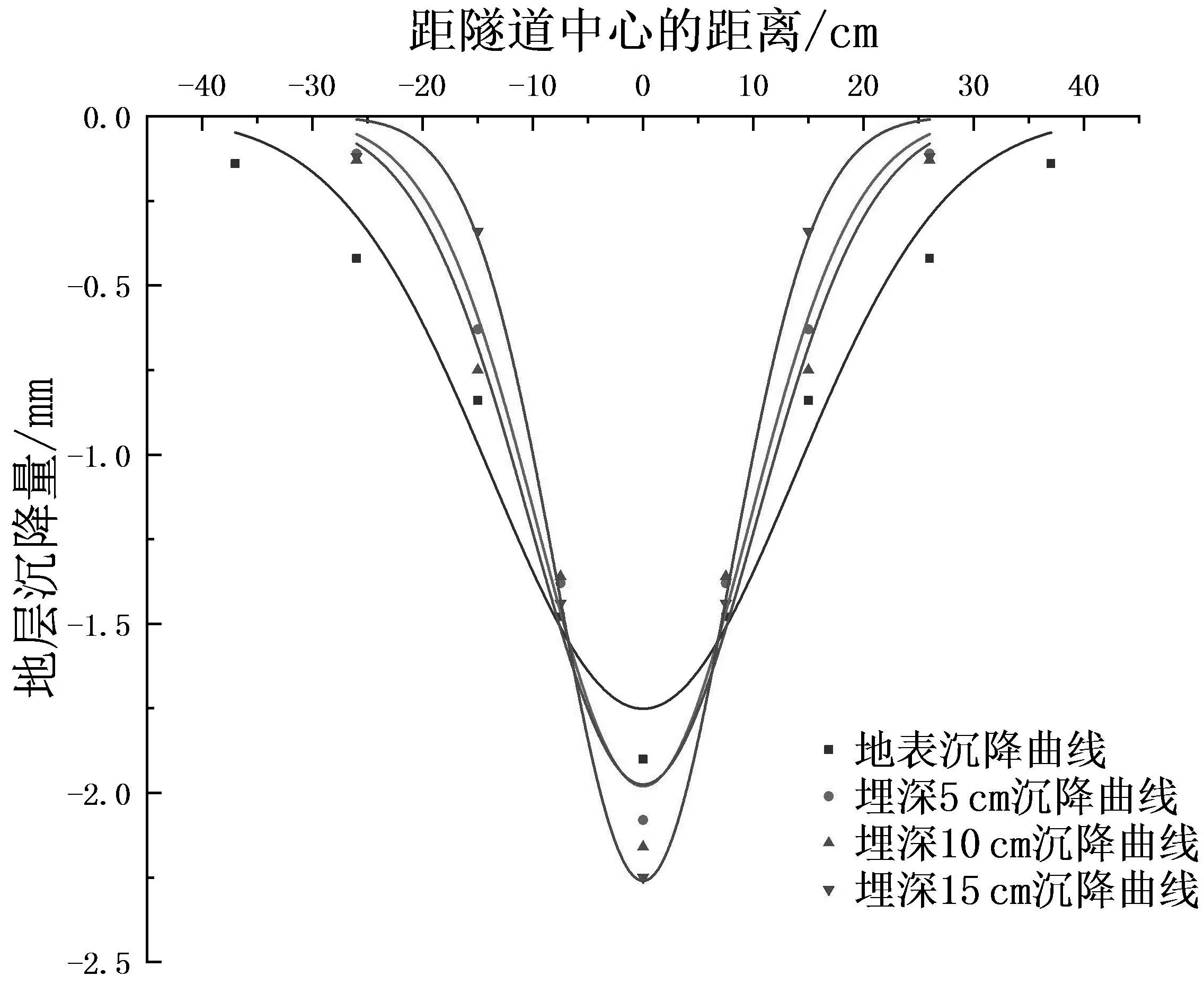
图9 5%地层损失率下地层沉降曲线

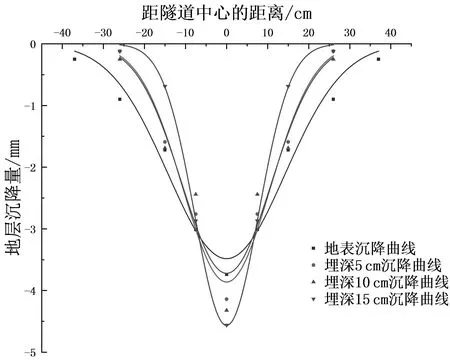
图10 10%地层损失率下地层沉降曲线

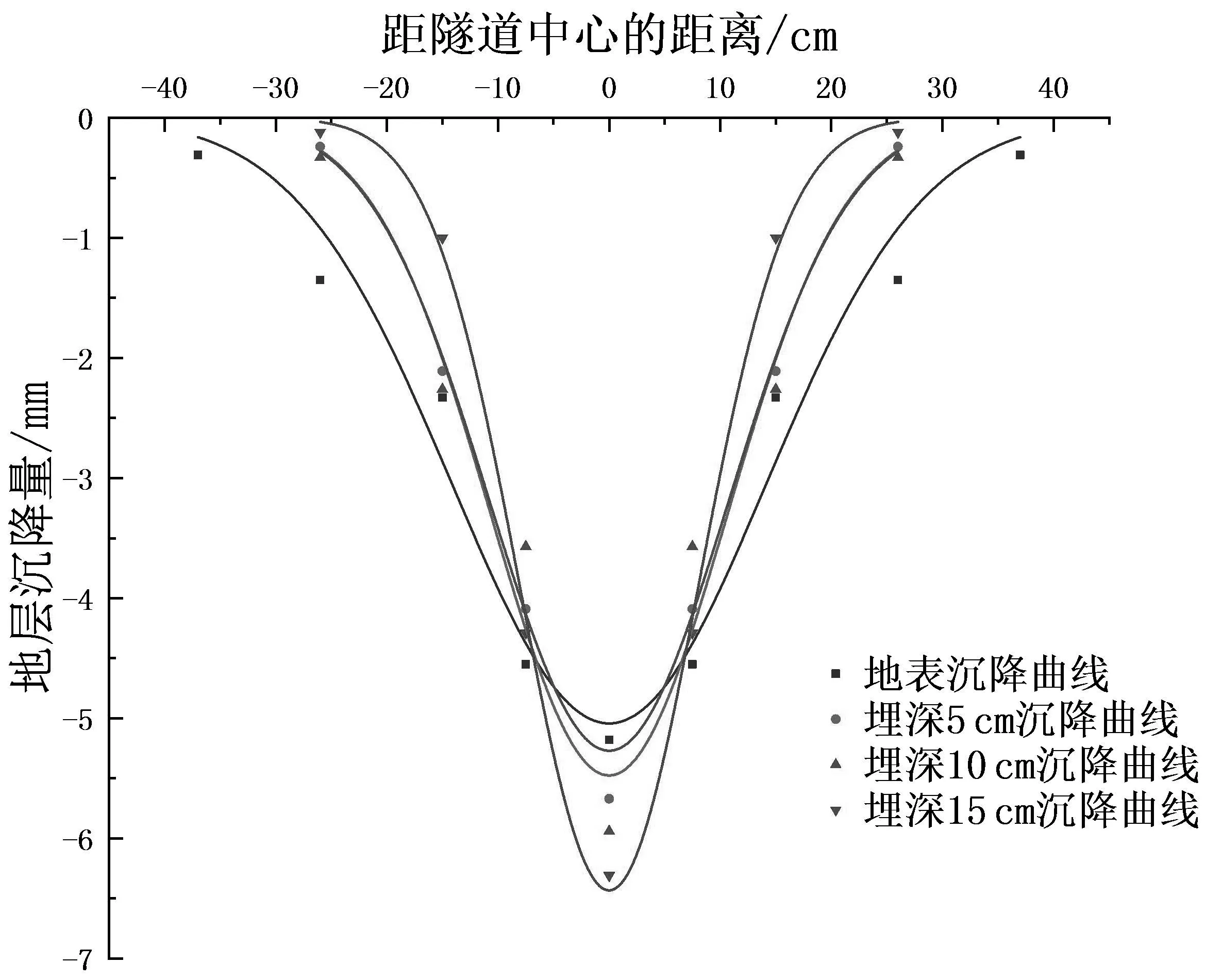
图11 15%地层损失率下地层沉降曲线

图12 20%地层损失率下地层沉降曲线

图13 25%地层损失率下地层沉降曲线

从图9至图13可以看出不同地层损失率下各深度处的地层沉降曲线均近似成高斯正态分布，用Peck公式进行拟合，如表2所示.

表2 不同地层损失率下地层沉降

用Peck高斯公式拟合，结果的决定系数为0.934～1.000，拟合效果较好.另外从图中可以看出，深度较大的位置处的中心沉降量较大，越靠近地表，中心最大沉降量减小的同时，沉降槽宽度系数增大，即沉降变形的影响范围增大.可以做出不同深度下最大沉降量及沉降槽宽度的曲线，如图14所示.

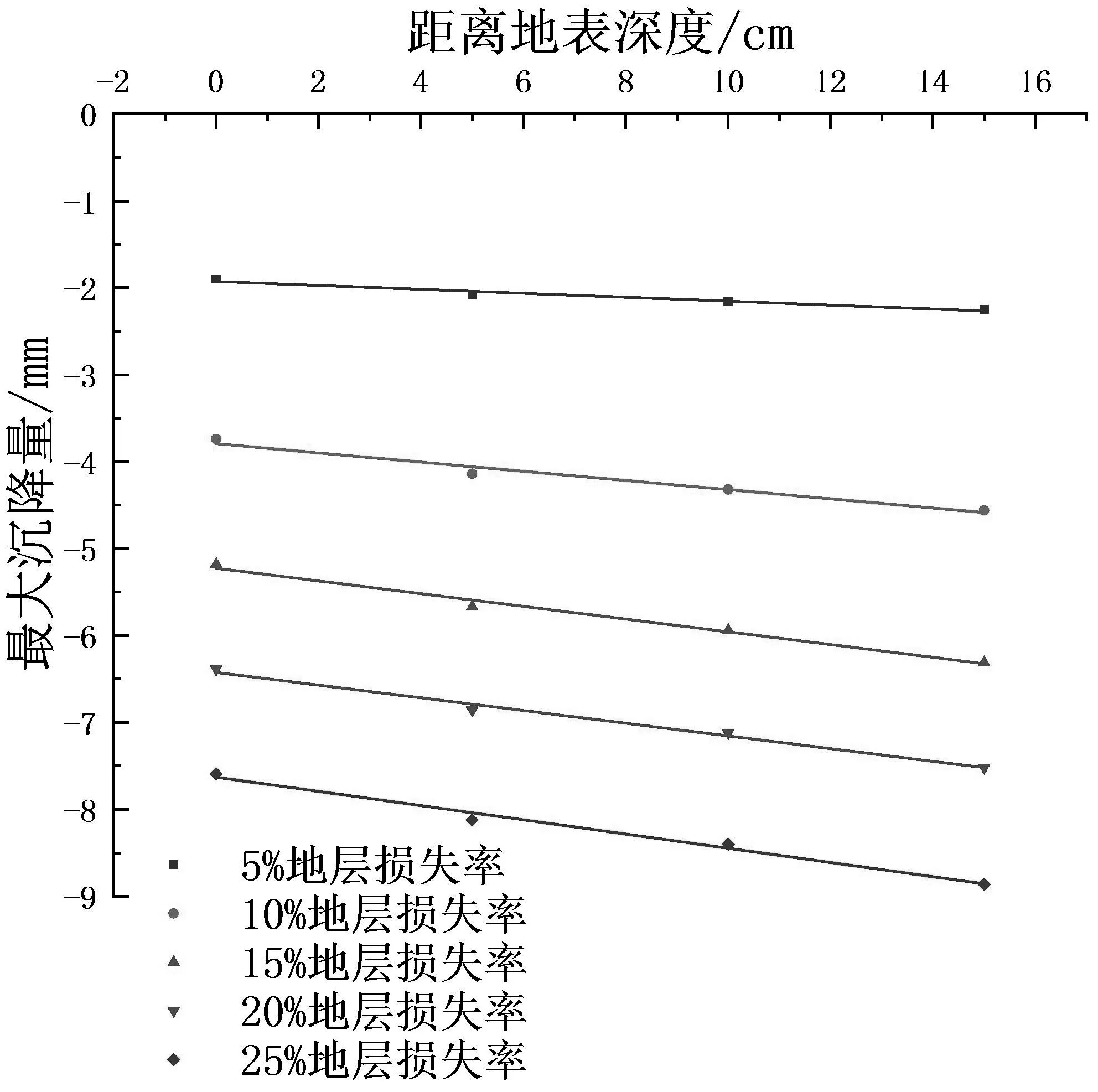
图14 不同深度下的最大沉降曲线

从图14可以看出，地表及地层内部最大沉降与地层深度呈线性关系，用一次函数进行拟合得到表3.可以看出，一次函数拟合效果很好，深度越大，最大沉降量越大.另外，地层损失率越大，直线斜率越大，这意味着随着地层损失率的增加，对地层内部的变形影响增大，地层变形的传递率增加.

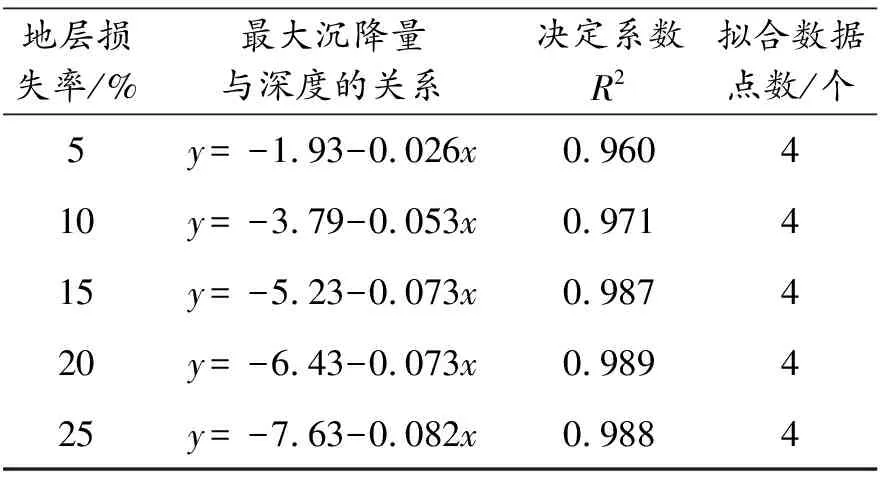
表3 地表及地层最大沉降量与深度的关系

O’Reilly等[14]认为地层沉降槽宽度系数i与h有关，其中h为隧道横轴线至地层的深度，本次试验测点一共布置四层，地表处测点h为30 cm，地层内部h依次为25 cm、20 cm和15 cm，本次实测试验数据通过Peck高斯公式的拟合效果良好，通过拟合结果可以得出各曲线的i值，并做出i与h的关系图,如图15所示.

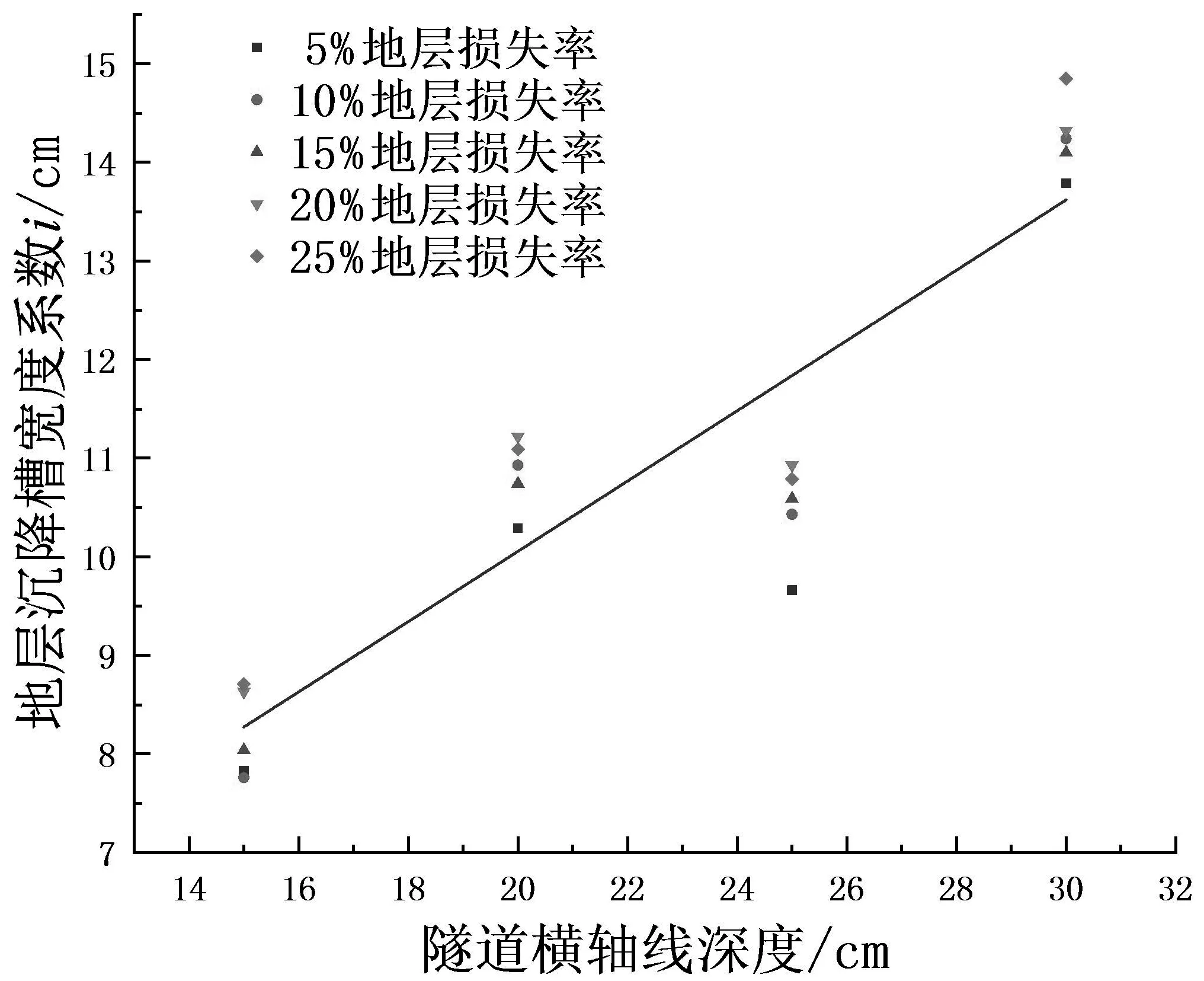
图15 沉降槽宽度系数与隧道横轴线深度关系图

通过回归拟合分析可以得到i与h的关系为式(3)：

i=2.92+0.356h

(3)

通过图15及式(3)可以看出，地层沉降槽宽度系数i与隧道横轴线至地层的深度h呈线性关系，地层沉降槽宽度系数随着h的增加而增加，地表处地层沉降槽宽度系数最大，沉降范围最广.

2.3 地层损失率对不同深度地层沉降槽体积影响

在计算隧道施工引起的地层损失时，一般假定在不排水条件下，地层损失即为地表沉降槽体积，即认为不同深度处沉降槽体积为常数，与地层损失量相等.本次试验地层损失量可通过排水量人为控制，地表及地层内部沉降槽体积可根据沉降曲线积分获得.由此可得到不同深度下的沉降槽体积曲线，如图16所示.

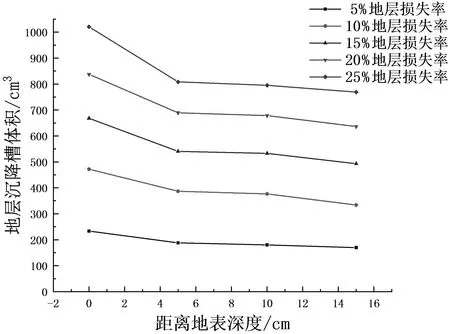
图16 沉降槽体积与地层深度关系图

结果显示，不同深度下沉降槽体积并非保持不变，地表处的沉降槽体积最大，随着埋深的增大，沉降槽体积减小.也就是说，地层直接损失引起的沉降槽体积有自下而上不断增大的趋势，但并非呈线性关系.可进一步根据王正兴等[8]定义的沉降槽体积传递率C进行分析，表达式为：

(4)

其中V为单位长度地层损失量，VS为单位长度地层沉降槽体积.可以做出不同地层损失率下，地层深度与沉降槽体积传递率之间的关系，如图17所示.

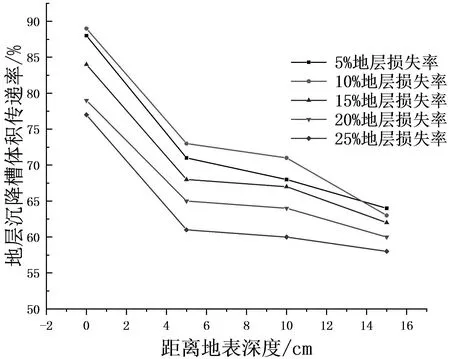
图17 沉降槽体积传递率与地层深度关系图

从图17可以看出，在不同地层损失率下，地表沉降槽体积传递率最大，随深度的增加，沉降槽体积传递率减小，与沉降槽体积的变化趋势基本一致，沉降变形的发生是一个自下而上的过程，沉降槽体积逐渐增大，砂土地层条件下沉降槽体积传递率均在60%至90%之间.对不同深度条件下不同地层损失率的地层沉降槽体积传递率进行离散性分析，结果如表4所示：

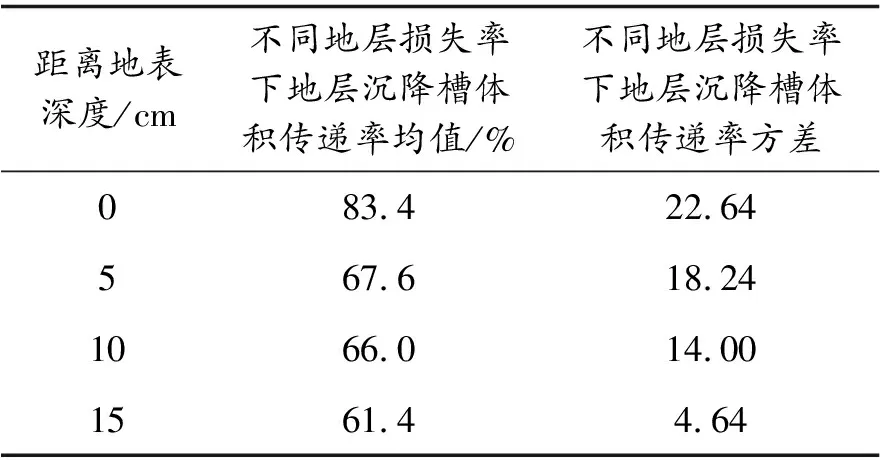
表4 地层沉降槽体积传递率离散性分析表

从表4可以看出，在地表阶段地层沉降槽体积传递率为83.4±7%，5 cm深度地层的地层沉降槽体积传递率为67.6±6%，10 cm深度地层的地层沉降槽体积传递率为66±6%，15 cm深度地层的地层沉降槽体积传递率为61.4±4%.同时随着地层深度的增加，不同地层损失率下地层沉降槽体积传递率的方差随之减少，数据更加集中,说明沉降槽体积传递率主要受地层深度影响，与地层损失率之间的关系并不明显.从前文图中还可看出，地层损失率较大时，沉降槽体积较大，而沉降槽体积传递率较小.说明随着地层损失的增大，沉降变形的体积向上传递的效率反而降低.推测原因为随着地层损失的增大，对周边土层的变形影响增大，水平位移的比例增大，竖向位移的比例较小造成表面上的传递效率降低.由于本试验只进行了竖向位移监测，该推断需要进一步的试验证实.

3 结论与展望

本次模型试验通过系统地进行不同地层损失率下的地层沉降变形研究，探讨了不同地层损失率下地层内部变形传递及地表变形规律，得到如下结论：

(1)影响地表沉降的直接因素是地层损失，不同地层损失率下，隧道轴线上方的地表沉降最大，地表沉降影响宽度约为5倍硐径，沉降槽符合高斯正态分布.地表最大沉降随着地层损失率的增加而增大，大致呈二次函数关系.地表沉降槽宽度系数随着地层损失率的增加而增大，沉降槽宽度系数在13.5～15范围之内，约为2倍硐径.

(2)在不同地层损失率下，不同深度处的沉降变形均符合高斯正态分布.其中，中心最大沉降与深度均呈线性关系，深度越大，最大沉降量越大.地层沉降槽宽度系数i与距离隧道横轴线的深度h呈线性关系，地层沉降槽宽度系数随着h的增加而增加，地表处地层沉降槽宽度系数最大.

(3)地层直接损失引起的沉降槽体积自下而上有增大趋势，但并非呈线性关系.砂土地层条件下沉降槽体积传递率的范围为60%～90%，沉降槽体积传递率主要受地层深度影响，与地层损失率之间的关系不明显.地层损失率较大时，沉降槽体积较大，而沉降槽体积传递率较小，推测为随着地层损失的增大，对周边土层的变形影响增大，水平位移的比例增大所造成.

(4)本研究对象为非黏性土地层内的地层变形，通过排液法可以人为有效地控制地层直接损失率，试验结果可完善地层损失率对地层变形的影响研究.另外，本次试验只进行了竖向位移监测，水平位移及应力监测有待进一步完善.