影响大学生考试作弊的相关因素分析——基于 SPSS 统计分析的实证研究
2022-03-22王洁
王 洁
影响大学生考试作弊的相关因素分析——基于 SPSS 统计分析的实证研究
王 洁
[作者:沈阳师范大学高等教育学硕士研究生]
近年来大学生作弊问题突出,出现了手机作弊、网络作弊等不良现象,作弊手段发生着新的变化,性质恶劣。学生考试作弊情况及其形成因素是复杂的。本文根据某大学一至四年级学生的专题抽样调查,并对获取数据进行描述性统计分析、相关分析和回归分析,用以探究影响大学生考试作弊行为发生的相关因素。结果表明,学生的学习能力与自身是否作弊情况的相关性较大。据此,就杜绝学生作弊行为发生提出一些建议。
SPSS;大学生;考试作弊;相关分析;回归分析
一、研究目的
越来越多的人能够有机会接受高等教育,受教育机会的增多为大学生个人发展带来了机遇。但不得不承认,一些在校大学生“迟到逃课” “课上睡觉”“考试作弊”甚至“学术造假”等问题在大学的校园里层出不穷。[1]学生的作弊手段也是越来越高级,出现了手机作弊、网络作弊等高科技作弊的手段。[2]甚者,出现了论文造假、学术造假的问题,在学生群体和网络中还出现了代课代考代写的专业群体,这些问题无疑不是个别大学生诚信严重缺失的体现。
笔者针对大学生诚信问题中的考试作弊情况展开调查研究,结合收集的数据,试图分析大学生考试作弊行为发生的相关影响因素,并就如何杜绝学生作弊行为发生提出一些建议。
二、相关设计
(一)研究方法
本研究采用问卷调查的抽样方法,调查大学生考试作弊的相关因素,将学生的年级、学习能力、道德教育、周围环境作为自变量,学生作弊情况作为因变量,并对变量进行赋值,进而采用SPSS软件对数据进行相关分析,研究影响大学生考试作弊的相关因素。
在自变量的设计中,将学生年级赋值,大一为1,大二为2,大三为3,大四为4;在调查学习能力时,询问学生认为自己的学生能力如何,设置很弱、弱、一般、强、很强五个选项,表示学习能力的由低到高,并分别赋值1、2、3、4、5;在调查学生是否接触道德教育课时,设置一次都没有、上过一两次、上过三次以上三个选项,表示学生接受道德教育程度的由低到高,并分别赋值1、2、3;在调查学生对周围考试作弊现象的感知中,询问学生周围考试作弊现象时,设置没有、很少、普遍三个选项,表示学生周围作弊现象的存在程度由低到高,并分别赋值1、2、3。
在因变量的设计中,询问学生是否有过作弊的想法或行为,并设置都没有、有想法没行动、都有三个选项,表示学生自身考试作弊程度的由高到低,并分别赋值1、2、3。
编制调查问卷,问卷采取不记名形式,每道题为单选,分发问卷进行调查。
(二)研究对象
研究对象为某大学一至四年级的学生,共发出问卷56份。
三、数据分析
(一)描述性分析
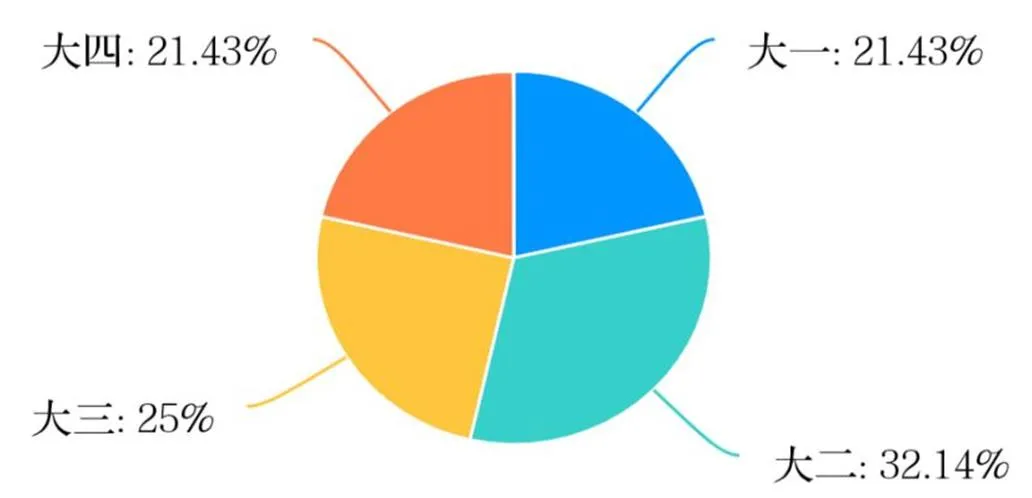
图1 年级分布图
使用SPSS软件对数据进行描述性统计分析,共收集一至四年级学生数据56份,年级情况分布如图 1年级分布图图 1。
在所有的被调查者中,12.5%的人认为自己学习能力很弱,19.64%的人认为自己的学习能力弱,41.7%的人认为自己的学习能力一般,23.21%的人认为自己的学习能力强,3.57%的人认为自己的学习能力很强。如图 2所示,大多数学生觉得自己的学习能力一般。
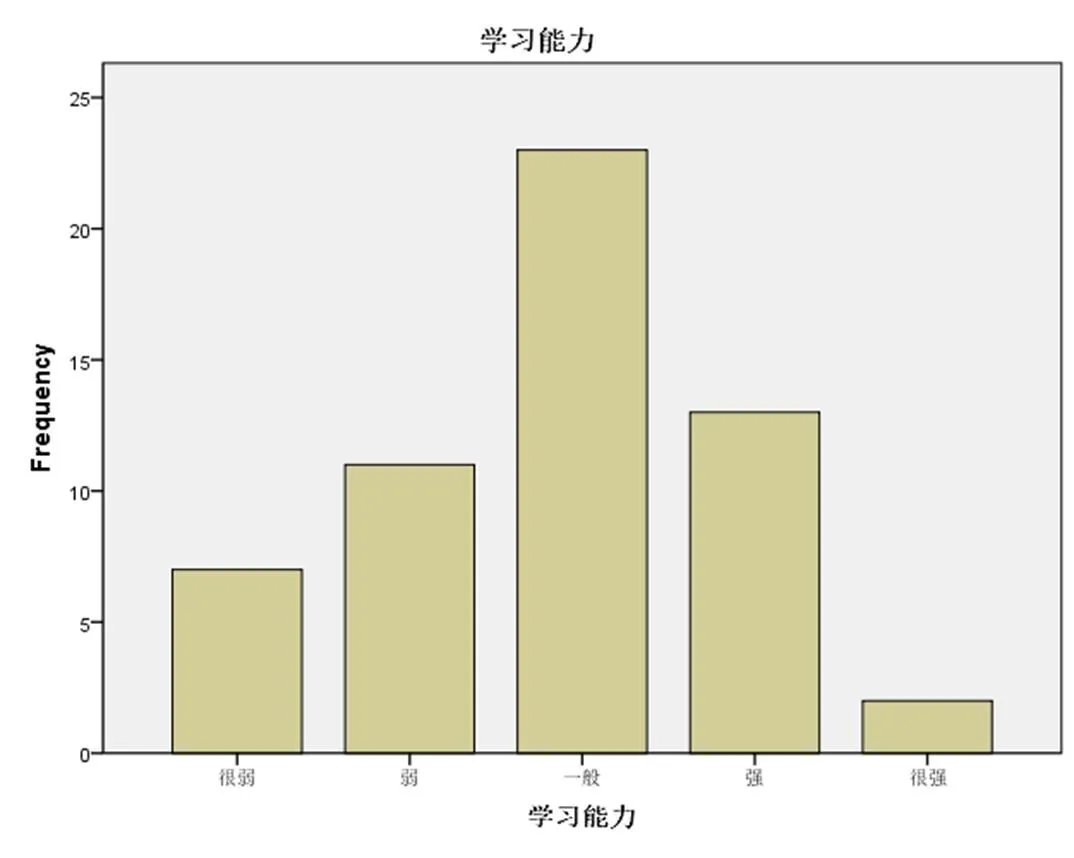
图2 学习能力条状图
14.29%的人一次都没有上过相关的道德教育课程,60.71%的人上过一两次道德教育课程,25%的人上过三次以上的道德教育课程。如图 3所示,大多数学生上过一两次道德课,极少数学生一次也没有上过道德教育课。对周围考试作弊情况的感知,10.71%的人认为身边没有作弊情况,67.86%的人认为周围考试作弊情况很少,21.43%的人认为周围考试作弊情况普遍。在调查被调查者自身是否有过考试作弊的想法和情况时,35.71%的人都没有,41.07%的人有想法没行动,23.21%的人都有。周围考试作弊情况与自身考试作弊情况关系如表1周围作弊情况与自身作弊情况交叉表表1。
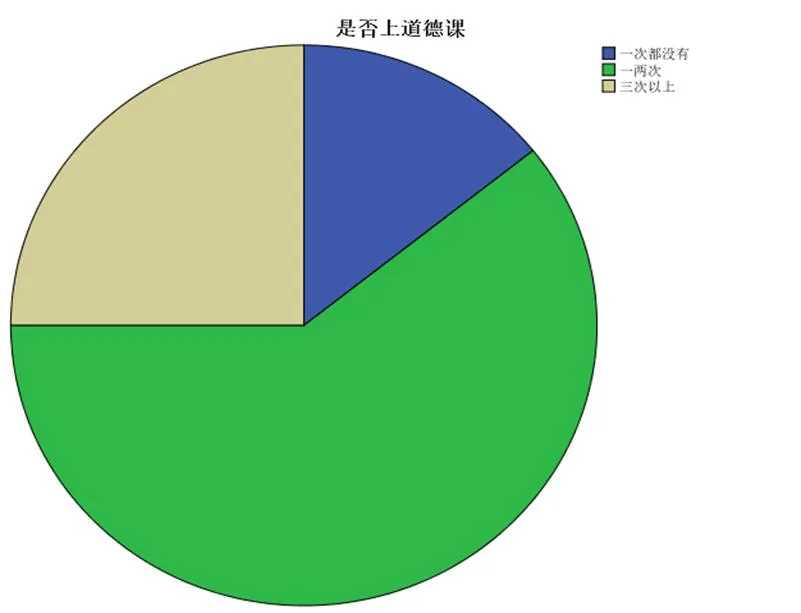
图3 道德课程上课情况
表1 周围作弊情况与自身作弊情况交叉表
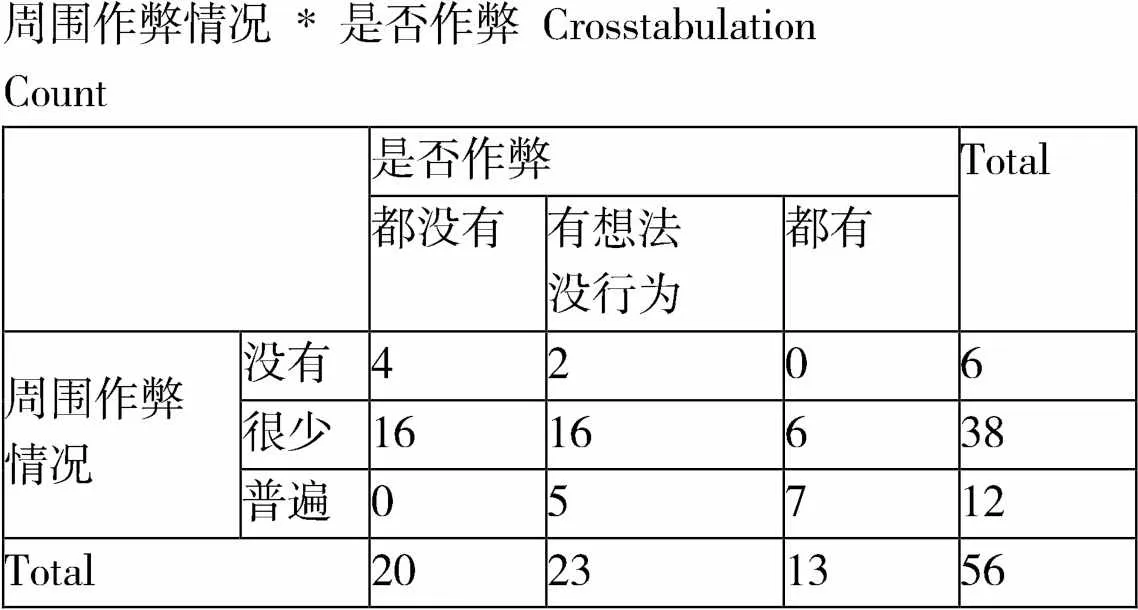
周围作弊情况 * 是否作弊 Crosstabulation Count 是否作弊Total 都没有有想法没行为都有 周围作弊情况没有4206 很少1616638 普遍05712 Total20231356
(二)相关性分析
使用SPSS软件分别对各个自变量与因变量之间进行相关性分析。选取相关性分析,采用双侧检验,得到相关系数。将年级情况与自身是否有作弊的想法和情况进行相关性分析,如表2所示,得到p值为0.344,0.344>0.05,说明两者关系是大概率事件。r值为-0.129,r值的绝对值<0.3,说明两者关系极弱,年级情况与是否作弊两者并不具有相关性。
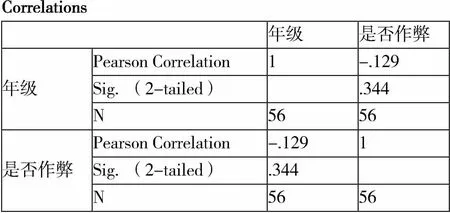
表2 年级与是否作弊相关性分析
将学习能力与是否作弊进行相关性分析,如表3所示,得到p值为0.000,0.000<0.01,说明进入了几小概率事件,r值为-0.690,而值的绝对值大于0.5小于0.8,说明两者中度相关。所以学习能力与是否作弊成负相关。学习能力越强,考试作弊的可能性越低。
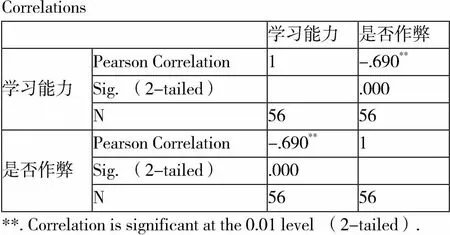
表3 学习能力与是否作弊相关性分析
将是否上过道德课与是否作弊进行相关性分析,如表4所示,得到p值为0.03,0.03大于0.01小于0.05,说明进入了小概率事件。r值为-0.391,r值的绝对值小于0.5大于0.3,说明两者低度相关,所以是否上过道德课与是否作弊呈负相关。上过的道德课次数越多,考试作弊的可能性越低。
表4 是否上过道德课与是否作弊相关性分析
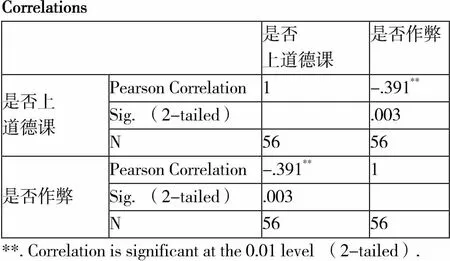
Correlations 是否上道德课是否作弊 是否上道德课Pearson Correlation1-.391** Sig. (2-tailed) .003 N5656 是否作弊Pearson Correlation-.391**1 Sig. (2-tailed).003 N5656 **. Correlation is significant at the 0.01 level (2-tailed).
将周围考试情况与是否作弊进行相关性分析,如表5所示,得到P值为0.000,0.000小于0.01,说明进入了几小概率事件。r值为0.498,0.498小于0.5大于0.3,说明两者低度相关。所以,周围作弊情况与自身是否作弊呈正相关。周围考试作弊情况越普遍,自身作弊可能性越高。
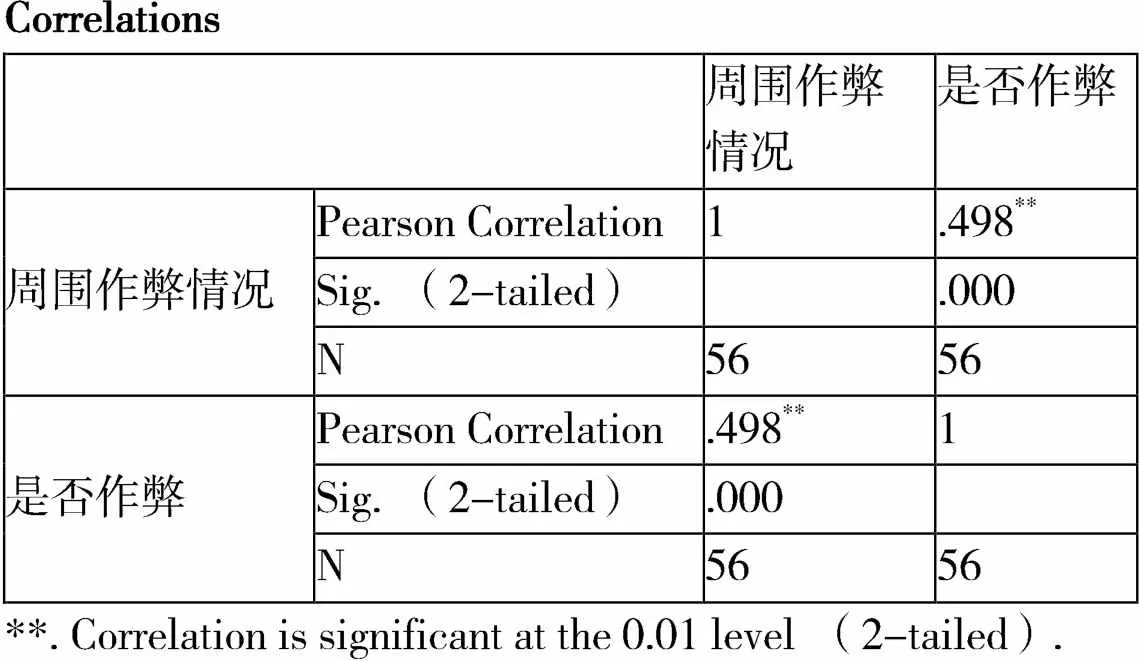
表5 周围作弊情况与是否作弊相关性分析
从上面的数据分析可知,学生的学习能力与其自身是否作弊情况的相关性较大,但还不能完全说明学习能力弱的同学,就一定容易发生考试作弊情况。为了使问题研究更加严谨,将学习能力与自身是否作弊进行回归分析,以提高分析结果的可靠性。根据回归分析原理,将大学生的学习能力当成自变量,是否作弊作为因变量,用SPSS软件进行操作可得。
表6表示两者相关系数为0.690,r的平方为0.476,用r表示学生的学习能力对自身是否作弊的拟合程度,学生学习能力对于自身是否作弊情况的拟合度较高,也就是说,该方程对于学生学习能力和自身是否作弊情况的线形关系的拟合程度是较高的。
表6 回归方程拟合程度
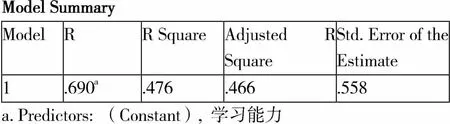
Model Summary ModelRR SquareAdjusted R SquareStd. Error of the Estimate 1.690a.476.466.558 a. Predictors: (Constant), 学习能力
表7表示对回归方程进行方差分析的结果,F值等于49.052,P值为0.000小于0.01,则该回归方程具有显著的统计学意义,也就是说该回归方程可以用来描述学生学习能力与是否作弊情况之间的关系。
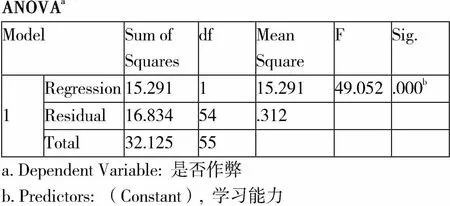
表7 回归方程方差分析
表8表示该回归方程的常数项和回归系数的显著性检验的t值和伴随概率值。两个P值均为0.000小于0.01。所以该回归方程的常数项与回归系数都达到了统计学意义,所以该方程为是否作弊等于3.331-0.510学习能力。
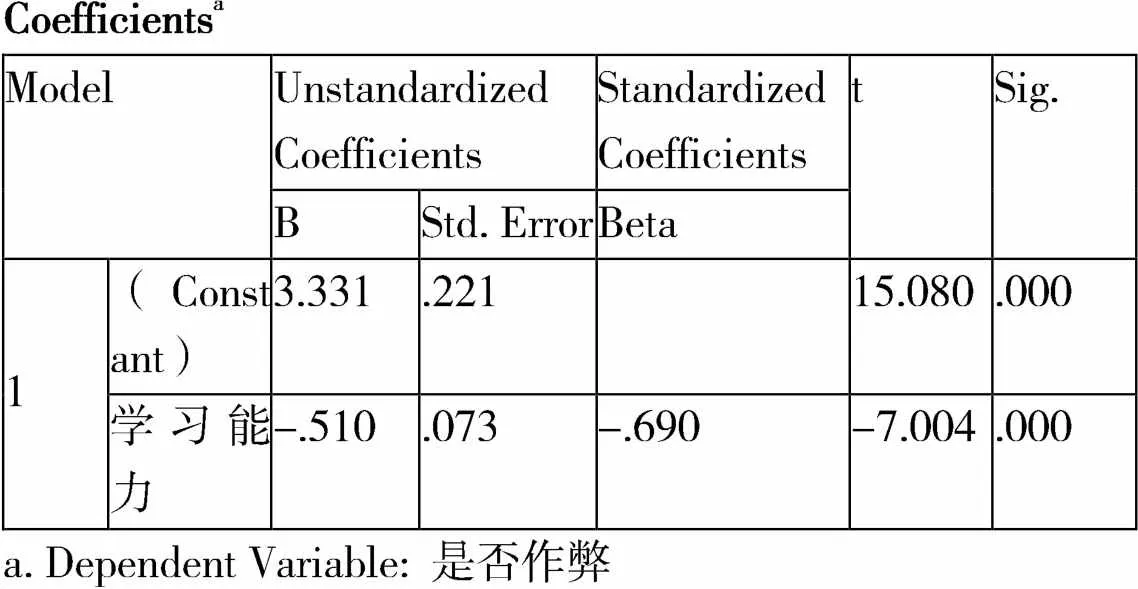
表8 回归方程
从相关分析和回归分析可得知,在保持其他因素不变的情况下,大学生的学习能力提高就会降低自身作弊情况。因此,提高大学生的学习能力,对促进大学生诚信考试有着显著的帮助作用。
四、结论与建议
通过问卷数据调查,对影响大学生考试作弊相关因素得出一些分析结论,并据此就杜绝学生作弊行为发生给出几点建议。
(一)研究结论
1.学习能力是影响大学生考试作弊情况发生的关键因素。
2.是否上过相关道德教育课程与大学生自身考试作弊情况呈负相关。
3.周围考试作弊情况越普遍,大学生考试作弊的可能性越高。
(二)几点建议
1.学校要注重培养大学生的学习能力,提升大学生的学习水平。学生只有自身学习能力不断提高,才能更好地规范自己的学术行为,探索更有价值的学习成果。学校应在学生录取时对其学习能力进行评测,教师在传授相关学习知识的同时,也要不断地培养提高学生的学习能力,使大学生真正具备相应的学习能力。
2.学校要提高道德教育课程的普及力度,注重学生的道德诚信培养。在增加相关道德教育课程数量的同时,也应注重提升道德教育课程的质量,真正地做到促进学生的德智体美劳全面发展。
3.学校要加大考试作弊检查力度以及强化惩戒考试作弊行为规范。如果学校不加以检查并惩戒考试作弊行为,只会使得学生考试作弊现象更为普遍。因此,学校应该注重对考试作弊行为的惩戒力度,为学生营造良好的学习环境以及校园文化。
[1]郭兰成.大学生诚信现状的反思与对策.中国高等教育[J].2007(08):23-30.
[2]熊平安.从考试作弊浅析当代大学生的诚信教育[D].武汉:华中师范大学.2007:5-17.
(责任编辑:杨书元)
