双叉式叶尖结构对风力机风轮振动的影响

代元军，贺凯，李保华，翟明成

(1. 上海电机学院机械学院，上海 201306； 2. 新疆农业大学机电工程学院，新疆 乌鲁木齐 830091； 3. 新疆工程学院能源工程学院，新疆 乌鲁木齐 830091)

当今社会正面临化石燃料枯竭和环境保护问题，迫切需要稳定和清洁的能源供应，于是人们便把目光投向了新能源[1].风能是新能源的一种，风力机通过风能带动风轮旋转，从而驱动发电机运行并产生电能.风轮是风力机的主要部件之一，风轮的设计应综合考虑环境、温度等情况，使叶片具有足够的强度和刚度，符合运行寿命要求，其中风轮运行过程中产生的振动对其损害较大，因此对风轮的振动研究成为研究热点[2].

在风力机风轮振动特性研究方面，孙国勇等[3]探究了利用动力学模态分解方法实现非定常流场的分解、 重构和预测.马剑龙等[4]和吕文春等[5]探究了翼型凹变对风轮叶片刚度及动频的影响，发现凹变可以提高风轮一阶、二阶固有频率及其阻尼比，且提升叶片静刚度与动刚度.蒋祥增等[6]研究了风力机风轮应变与塔架振动之间关系机制.武浩[7]以数值模拟的方法探究了高风速下风力机振动特性变化规律.代元军等[8]对V形叶尖改型叶片风轮进行模态试验和动态振动特性试验.张立等[9]研究了考虑自重对大型风力机复合材料叶片结构力学特性影响.HAGHDOUST等[10]研究了在风力机叶片材料里加入形状记忆合金来抑制风力机的振动.CHEN等[11]设计了一种调谐液体阻尼器来抑制风力机振动.JOKAR等[12]建立水平轴风力机襟翼方向叶片的动力学模型并对其开展振动分析.LORENZO等[13]介绍了一种基于风力机叶片振动的叶片裂纹识别方法.根据文献研究可知，目前对于风力机风轮振动特性的研究比较热门，但是从叶片设计角度研究风力机风轮振动特性较少.

风力机叶片叶尖是载荷变化最强烈的地方，所以改型设计主要针对叶尖.文中提出一种双叉式叶尖改型设计方案，探究双叉式叶尖结构对风力机风轮振动特性的影响.双叉式叶尖结构的改型设计思路来源于民用客机的双叉式叶尖结构机翼，双叉式叶尖结构机翼可削减翼尖涡强度，从而增强机翼的气动性能与结构动力学特性.试验所用风轮为课题组设计并通过正交试验开发，风能利用系数及功率较好的一组，相关研究结论可为小型风力机风轮的减振研究提供一种新思路.

1 试验方案设计

对于双叉式叶尖结构风力机风轮的振动特性研究，共进行两项试验，一项是风轮模态试验，探究双叉式叶尖结构改型设计后对风轮静态振动特性的影响.另一项是风轮振动特性试验，探究双叉式叶尖结构改型设计后对风轮动态振动特性的影响.

1.1 风轮模态试验方案设计

1.1.1 被测对象

试验采用100 W小型风力机叶片，风轮叶片数为三叶片，未改型叶片与双叉式叶尖结构叶片三维图见图1.额定来流风速设计为8 m/s，额定转速设计为600 r/min，叶片参数：z为叶片数，z=3;l为叶片长，l=0.65 m；d为风轮直径，d=1.3 m；额定叶尖速比为5,叶尖弦长为0.041 m，最大展弦比为4.14,相对厚度为10.26%，叶片翼型为S825.

图1 叶片三维图

双叉式叶尖结构包括叶尖夹角θ，叶尖长度a和叶尖宽度h.叶尖结构见图2，叶尖结构1，2，3的叶尖长度都为47 mm,叶尖宽度分别为24.0,45.0,63.5 mm,夹角分别为30°,60°和90°.

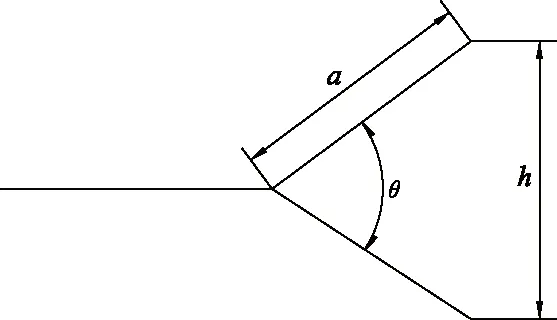
图2 双叉式叶尖结构

1.1.2 试验设备

力锤采用B&K8206型敲击力锤，加速度传感器采用4507-B-004加速度传感器，数据采集系统由3660-C-1005模块无线LAN机箱和3053-B-12/型高密度12通道数据采集前端组成.试验设备如图3所示.

图3 风轮模态试验设备

1.1.3 试验方法

采用瞬态激振法，手持力锤对叶片施加激励，叶片受激励后振动产生的原始振动信号由BK振动测试分析系统中的18个加速度传感器组成的振动传感器阵列采集，并由数据采集前端与无线LAN机箱组成的数据采集系统对采集到的原始信号保存、转换并传输给计算机，通过测试系统中的BK Connect软件完成对数据的处理分析，数据分析后可得到叶片的模态参数.

1.1.4 测点布置

为激励出风轮所有模态参数，试验采取多点激励、多点响应方法.在叶片相关位置布置18个测点，测点布置如图4所示，1—18为加速度传感器布置点，19—33为力锤激励点.风力机风轮振动疲劳破坏与共振通常发生在低阶，所以模态测试加速度传感器频率测试范围选择为0～400 Hz，适合此频率范围力锤为橡胶头力锤，设置力锤激励触发量级为15 N，每个力锤激励点的激励次数为5次.BK Connect软件自带敲击检查功能，当检测到的触发量级与设置一致时，会对原始振动数据进行保存，当检测到的触发量级与设置不一致时，会提示重新激励且不记录数据，此功能有效的保证触发量级的准确性.

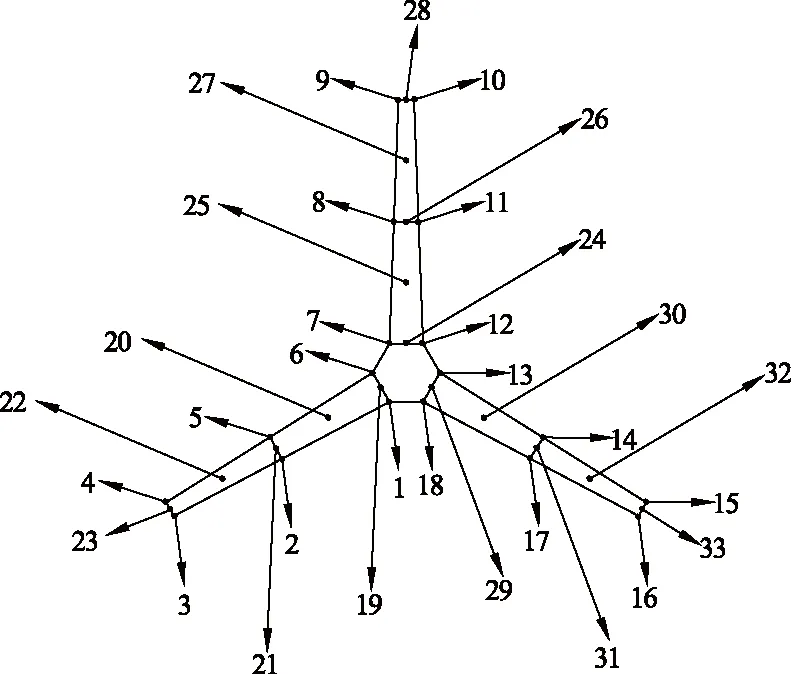
图4 风轮模态试验测点布置图

1.2 风轮振动特性试验方案设计

1.2.1 试验设备

被测对象与风轮模态试验一致，风轮振动特性试验在风洞实验室进行，采用直流低速风洞，开口段最大风速为15 m/s，开口段尺寸为19.5 m×3.0 m×3.0 m.三向加速度传感器采用B&K公司的4524-B型，此型号传感器采用CCLD供电.为了便于后期的数据处理，接入激光测速探头来获取转速信息，激光测速探头采用B&K公司的2981型，此型号测速探头采用CCLD供电.为实现试验所需的工况，需接入电子负载仪来调节风力机风轮的转速，电子负载仪采用爱德克斯公司的IT8512A+型，试验设备如图5所示.

图5 风轮振动特性试验设备

1.2.2 试验方法

采用频谱分析法，先将风力机安装在风洞前，风轮旋转平面距离风洞开口端平面0.5 m，风轮旋转中心对准风洞开口端中心，调节风洞以一定的风速工作，风轮受气动载荷作用而旋转时，用BK振动测试分析系统中的三向加速度传感器组成振动测试系统采集风轮的原始振动数据，并由数据采集系统对采集到的原始信号保存、转换并传输给计算机，通过测试系统中的BK Connect软件完成对数据的处理分析，通过数据处理结合频谱分析法，即可得到风轮的振动频率与振动加速度幅值.

1.2.3 测点布置

测点布置如图6所示，一共布置2个三向加速度传感器，分别位于发电机靠近风轮的前端与中端，通过振动特性试验得到的动态振动频谱图结合模态试验得到的静态振动频谱图并运用频谱分析法可识别出风轮的振动频率与振动加速度幅值.通过对比分析静态振动频谱图与动态振动频谱图，发现位于发电机前端加速度传感器的动态振动频谱图与静态振动频谱图相似度较高，故数据分析以发电机机头前端的加速度传感器为准.

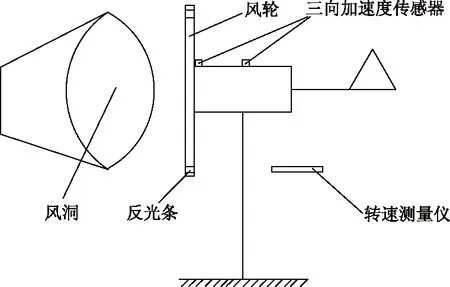
图6 风轮振动特性试验测点布置图

2 试验数据分析

试验数据采用BK Connect软件进行处理，风轮模态试验的数据通过软件的分析模态模块处理，采用Rational Fraction Polynomial-Z的算法进行整体求解，最大迭代40次，可计算出所需的模态参数.风轮风洞试验通过软件的数据处理模块对原始振动信号进行快速傅里叶变换，通过频谱分析法可得到风轮的振动频率与振动加速度幅值.

2.1 双叉式叶尖结构对风轮模态参数的影响分析

2.1.1 固有频率

图7为风轮各阶固有频率fn曲线，双叉式叶尖结构风轮整体的固有频率规律增大.与未改型风轮相比，双叉式叶尖结构风轮一阶固有频率降低，二阶至四阶固有频率增大，五阶、六阶规律性不明显.固有频率改变会影响结构的共振特性，当风轮外界激振频率接近或等于固有频率时，风轮便会发生共振.所以双叉式叶尖结构使风轮二阶至四阶固有频率提高，使风力机风轮共振发生的概率变低.

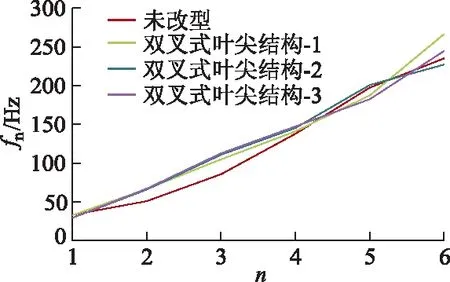
图7 风轮各阶固有频率

通过上述分析可知，双叉式叶尖结构能使风轮二阶至四阶固有频率规律增大，结合数据分析可知：与未改型风轮相比，双叉式叶尖结构-1风轮在二到四阶固有频率分别提高30.87%，22.31%，2.15%，双叉式叶尖结构-2风轮在二到四阶固有频率分别提高29.39%，29.40%,5.45%，双叉式叶尖结构-3风轮在二到四阶固有频率分别提高31.48%，31.46%，6.84%，双叉式叶尖结构风轮在二阶到四阶的固有频率得到明显的提高.其中双叉式叶尖结构-3风轮的提升效果最好，此规律对以后降低风轮振动有一定的参考价值.

2.1.2 阻尼比

图8为风轮各阶阻尼比ζ曲线，双叉式叶尖结构风轮整体的阻尼比规律增大.与未改型风轮相比，双叉式叶尖结构风轮一阶阻尼比降低，二阶至四阶阻尼比增大，五阶、六阶规律性不明显，此规律性与固有频率类似.阻尼比表示结构在受激振后振动的衰减形式，对于风力机风轮，阻尼比越大结构稳定性越好.所以双叉式叶尖结构使风轮二阶至四阶阻尼比提高，使风轮更具稳定性，改良了风轮的静态振动特性.

通过上述分析可知，双叉式叶尖结构能使风轮二阶至四阶阻尼比规律增大，结合数据分析可知：与未改型风轮相比，双叉式叶尖结构-1风轮在二到四阶阻尼比分别提高147.88%，22.53%，23.81%，双叉式叶尖结构-2风轮在二到四阶阻尼比分别提高186.06%，40.66%，30.77%，双叉式叶尖结构-3风轮在二到四阶阻尼比分别提高407.88%，10.99%，80.59%.双叉式叶尖结构风轮在二阶到四阶的阻尼比得到明显提高，其中双叉式叶尖结构-3风轮的提升效果最好，且双叉式叶尖结构-1风轮的提升效果最差.

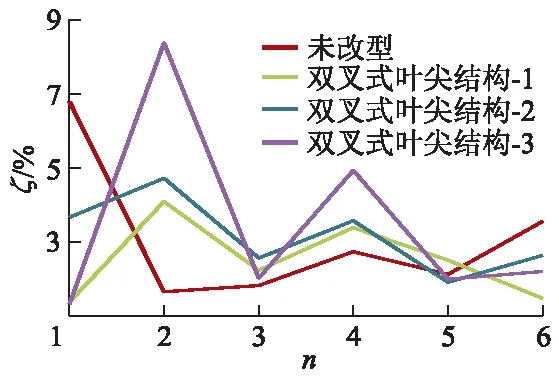
图8 风轮各阶阻尼比

2.2 双叉式叶尖结构对风轮振动特性的影响分析

2.2.1 坎贝尔图分析

分析坎贝尔图横坐标为转速，纵坐标为动频频率.图中射线为激振频率射线(风轮基频的n整数倍)，对于三叶片风力机，认为基频的三倍频(3P)为主激振源频率，所以将主激振源频率的±10%区域设置为共振区.振动频率曲线与共振区2个交点所对应频率之间的差值为振动频率曲线穿过共振区的频宽，振动频率曲线与3P交点对应的转速即为共振点所对应的转速.振动频率曲线穿过共振区的频宽越宽，共振点所对应的转速越接近额定转速，证明共振概率越大，反之则越小.

因为风力机的共振一般发生在低阶，所以振动特性试验数据分析以一阶振动频率为主要分析对象.图9为风轮一阶坎贝尔图.风轮振动频率fv随着转速增大而升高，通过软件数据定位，可知未改性风轮振动频率曲线穿过共振区的频宽为0.97 Hz，共振点所对应转速为362.68 r/min，双叉式叶尖结构-1风轮振动频率曲线穿过共振区的频宽为0.86 Hz，共振点所对应转速为358.96 r/min，双叉式叶尖结构-2风轮振动频率曲线穿过共振区的频宽为0.74 Hz，共振点所对应转速为356.99 r/min，双叉式叶尖结构-3风轮振动频率曲线穿过共振区的频宽为0.65 Hz，共振点所对应转速为351.52 r/min.通过对比分析可知双叉式叶尖结构风轮振动曲线穿过共振区的频宽较未改型风轮更窄，双叉式叶尖结构可使风轮进入共振区的时间变短，使风轮更快脱离共振区.双叉式叶尖结构风轮共振点所对应的转速较未改型风轮更远离额定转速，使风力机风轮发生共振的概率变小.其中双叉式叶尖结构-3风轮振动频率曲线穿过共振区的频宽最窄，且共振点所对应的转速远离额定转速最多，所以双叉式叶尖结构-3风轮的改型效果最好.此外还进行了风轮二阶坎贝尔图分析，得到的结论与一阶相似.

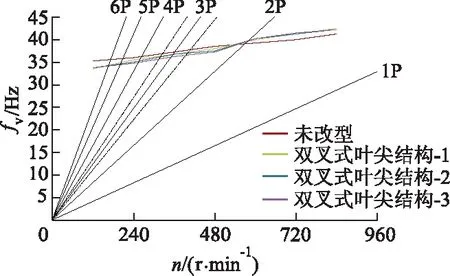
图9 风轮一阶坎贝尔图

2.2.2 振动加速度幅值分析

图10为风轮一阶振动加速度幅值a曲线，风轮整体的一阶振动加速度幅值增大，在转速为360 r/min时一阶振动加速度幅值产生突增，分析原因是试验风轮的共振转速为351～363 r/min，共振使风轮的一阶振动加速度幅值产生突增.通过对比分析可知，双叉式叶尖结构不会使一阶振动加速度幅值的突增消失，而是降低突增时振动加速度幅值的数值，结合图9的坎贝尔图分析可知双叉式叶尖结构不会使风轮的共振消失，而是使风轮能够更快速地穿过共振区，减小共振加速度幅值.

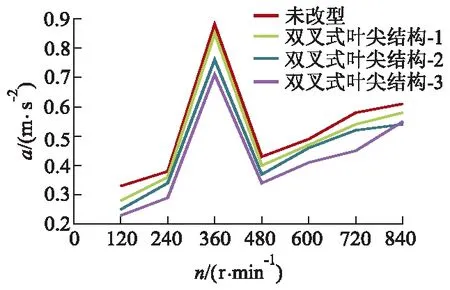
图10 风轮一阶振动加速度幅值

与未改型风轮相比，在共振转速为360 r/min和额定转速工况为600 r/min时，双叉式叶尖结构-1风轮的一阶振动加速度幅值分别降低3.41%和4.08%，双叉式叶尖结构-2风轮的一阶振动加速度幅值分别降低13.64%和6.12%，双叉式叶尖结构-3风轮的一阶振动加速度幅值分别降低19.32%和16.33%，通过以上在共振转速与额定转速工况下对比分析风轮的振动加速度幅值可知，双叉式叶尖结构可以降低风轮的振动，其中改型效果最好的双叉结构-3风轮，其整体的一阶振动加速度幅值最低.

3 结 论

1) 通过对风轮固有频率与阻尼比的分析可知，双叉式叶尖结构能使风轮二阶到四阶的固有频率与阻尼比规律增大，双叉式叶尖结构可改良风轮的静态振动特性.

2) 通过对风轮的坎贝尔图与振动加速度幅值分析可知，双叉式叶尖结构不会使风轮的共振消失，但可以使风轮进入共振区的时间变短，风轮更快地穿过共振区，共振点所对应的转速远离额定转速且可降低风轮的振动加速度幅值.

3) 找到双叉式叶尖结构的叶尖夹角是影响振动特性改良效果的主要因素，在0°～90°内，叶尖夹角越大的双叉式叶尖结构的改良效果越好，其双叉式叶尖结构-3风轮具有最佳的减振性能.