气液两相流工况下泵内气相特征数值计算
2022-03-22刘厚林杜欣来吴贤芳谈明高
刘厚林,杜欣来*,吴贤芳,谈明高
(1. 江苏大学国家水泵及系统工程技术研究中心, 江苏 镇江 212013; 2. 江苏大学能源与动力工程学院, 江苏 镇江 212013)
population balance equation;numerical simulation
叶片泵输送的介质并不局限于纯液体,在某些工业生产过程中,会产生气液混合物,如油气输送、核反应堆、污水处理、生物化学反应等.双叶片泵主要用于污水处理过程中,在污水中容易存在气体,包括硫化氢、甲烷等,当气体进入泵内,会影响泵系统的稳定运行,如果不能及时排出,将导致污水泵能量性能和内流性能下降[1].
在叶片泵内气液两相流数值模拟广泛采用双流体模型(two-fluid model,TFM)[2],文献[3-5]基于TFM模型对叶片泵内气液两相流动进行了数值模拟研究.但TFM模型采用固定气泡尺寸,在高含气率下精度较低,忽略气相的破碎、聚并行为,也不能很好地反映流体之间的相互作用.
HULBURT等[6]率先提出在气液两相计算中使用群体平衡模型(population balance model,PBM),清楚地描述了气泡的尺寸分布及气泡的聚并、破碎现象,该模型已广泛应用于多组分离散气泡和液体流动的数值模拟研究[7-9].戈振国[10]和YAN等[11]分别在Fluent软件中采用CFD-PBM模型对离心式混输泵内气相分布进行了模拟,并采用离散法求解群体平衡方程,研究了泵内气相分布、速度分布和压力分布等.LO[12]在TFM模型和PBM模型的基础上提出多尺寸组(multiple size groups,MUSIG)模型,并在ANSYS-CFX软件中得到应用,其采用离散法求解群体平衡方程,将气相按照尺寸大小离散为一系列气泡组,然后建立各气泡组的群体平衡方程.
综上所述,与TFM模型相比,群体平衡方法具有许多优势,能够获得气泡或液滴的尺寸分布,计算结果更符合实际.为此,文中采用均一MUSIG模型对叶片泵内气相的运动、分布规律进行研究,将气相按照尺寸大小划分为10组不同直径的气泡组,分析不同直径气泡的分布规律以及平均直径气泡在泵内流道的分布规律等.
1 数值模型
CFD模型采用以TFM模型为基础的MUSIG模型,耦合Prince-Blanch模型[13]和Luo-Svendson模型[14]描述气泡聚并和破碎过程.液相湍流模型采用SSTk-ω模型,气相采用零方程理论模型.
1.1 TFM模型
TFM模型的控制方程包括连续性方程和动量方程,即

(1)

∇·τq+αqρqg+Mq,
(2)
式中:αq为第q相的体积分数;ρq为第q相的密度;vq为第q相的速度;p为所有相的压力;τq为第q相的应力张量;g为重力加速度矢量;Mq为由于界面力(考虑了阻力和升力)引起的连续相和分散相之间的动量交换.
1.2 均一MUSIG模型
1.2.1 群体平衡方程
群体平衡方程是利用MUSIG模型进行数值模拟的基础,它是描述多相流动系统中颗粒分布随时间、空间连续变化的偏微分方程,其表达形式为
BB-DB+BC-DC,
(3)
式中:Ui为气泡的运动速度;n(m,t)为单位时间、单位空间内颗粒数量的分布函数;BB,DB,BC,DC分别为由于气泡破碎或聚并而导致的数量变化.
那,难道她有点爱上了老易?她不信,但是也无法斩钉截铁地说不是,因为没恋爱过,不知道怎么样就算是爱上了。
1.2.2 各组质量方程
(4)
1.3 气泡破碎模型
Luo-Svendson模型建立了多相湍流弥散系统中离散相的破碎理论模型,其假设气泡都是二元破碎.破碎是由涡的能量水平决定的,当涡的长度尺度与气泡直径相比较小或相当时,会诱发振荡.以质量表示的气泡破碎速率计算公式为
(5)
其中
(6)
式中:fBV为随机破碎体积分数;ζ为各向同性湍流惯性子区间中涡的量纲一尺寸,ζ=λ/di;FB为修正系数;εc为连续相涡流耗散率;σ为表面张力系数;β为常数,取β=2.0.
1.4 气泡聚并模型
Prince-Blanch模型考虑了湍流随机碰撞对气泡聚并的影响,由气泡的碰撞频率和碰撞导致聚并的概率可求出气泡的聚并率.以质量表示的气泡聚并速率计算公式为
(7)
2 几何模型和数值计算方法
2.1 模型泵
以一台双叶片泵为研究对象,其主要设计性能参数分别为流量Qd=41.4 m3/h,扬程H=7.0 m,转速n=1 200 r/min,比转数ns=111;主要设计几何参数分别为叶轮进口直径D1=90.0 mm,叶轮出口直径D2=201.0 mm,叶轮出口宽度b2= 45.0 mm,叶轮叶片数Z=2.模型泵的计算域如图1所示.

图1 模型泵计算域
2.2 网格划分及边界条件设置
采用前处理软件ICEM CFD对模型泵流体计算域网格进行绘制,并进行网格无关性验证. 采用ANSYS-CFX软件进行流场数值计算[15-16],其中进口边界条件设置为压力进口(101.325 kPa),并给定入口气体体积分数IGVF,出口边界条件为质量流量出口.
将气相划分为10组气相粒组,气泡尺寸等直径离散分布,气泡直径分别为0.50,0.72,0.94,1.17,1.39,1.61,1.83,2.06,2.28,2.50 mm.进口气相直径设为1.39 mm.为描述初始两相工质的组分,定义入口气体体积分数为
IGVF=Qg/(Qg+Ql),
(8)
式中:Qg为气体体积流量;Ql为液体体积流量.
气液两相流工况下泵的扬程H为
(9)
式中:Hl,Hg分别为对液体、气体产生的扬程.
3 计算结果与分析
3.1 压力分布
图2为液体流量1.0Qd,IGVF分别为1.0%,2.0%和3.0%时叶轮流道中间截面的压力分布,可以看出,随着入口气体体积分数增大,靠近叶片吸力面的流道内低压区面积逐渐增大,而工作面高压区面积逐渐减小.这是由于气体的存在减少了流道面积,使得叶片对水做功减少,且增加了流动损失,从而使叶轮增压能力变弱.
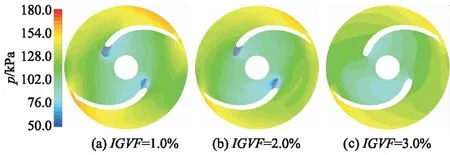
图2 设计工况下不同进口气体体积分数时叶轮流道中间截面压力分布
3.2 气相体积分数分布
图3为液体流量1.0Qd,IGVF分别为1.0%,2.0%和3.0%时泵内流道中间截面的气相体积分数分布,可以看出:整体上,叶片吸力面和蜗壳靠近出口处气相体积分数较大,IGVF=1.0%,2.0%和3.0%时,泵内最大气相体积分数分别为85.6%,89.2%和99.9%;随着入口气体体积分数的增大,叶片吸力面高气相体积分数区域面积增加,叶轮和蜗壳流道内气相弥散区域面积扩大;当入口气体体积分数达到3.0%时,叶片吸力面较大面积区域内气体体积分数超过80.0%,蜗壳近壁区气体体积分数低于1.0%,这是因为叶片吸力面是低压区,由于压力梯度的作用,气相容易在叶片吸力面聚集形成气团,而在蜗壳近壁区内,静压较大,且液相受惯性力作用而集中在蜗壳壁面附近,所以蜗壳近壁区气体体积分数极低.
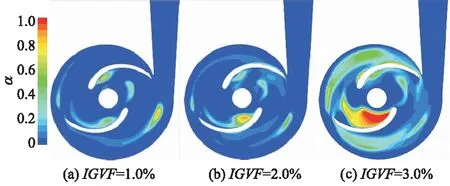
图3 设计工况下不同进口气体体积分数时叶轮流道中间截面气相体积分数
图3中2个叶片吸力面气相体积分数大小有一些差异,位于下方的叶片吸力面气相聚集区内气相体积分数较大,这主要是由于位于上方的叶片掠过蜗壳出口,大部分气体随液相运动而离开叶轮和蜗壳流道.
3.3 不同直径气泡分布
图4为液体流量1.0Qd,IGVF=3.0%时,泵内流道中间截面的气相粒组分数AGSF分布.可以看出,叶轮进口区域和叶片吸力面气相聚集区内主要是大直径气泡,而叶片吸力面气相尾迹区、蜗壳近壁区和蜗壳出口段内主要为小直径气泡,几乎没有直径大于1.39 mm的气泡.这是因为在泵进口段,流场压力较低,气液相间的相对速度较低,气泡受到的相间作用力较弱,容易发生聚并行为,因此气泡尺寸较大.叶片吸力面是低压区,气泡集中度高,气泡容易聚并形成大直径气泡,而在气相尾迹区,流动较为紊乱,气泡容易破碎为小直径气泡.在蜗壳近壁区内,气泡间距较大,直径较小.在蜗壳出口,流场压力较大,气泡破碎的概率较大,故能保持较小直径.

图4 设计工况下IGVF=3.0%时气相粒组分数分布
3.4 气泡平均直径分布
图5为液体流量1.0Qd时,IGVF分别为1.0%,2.0%和3.0%时泵内流道中间截面的气泡平均直径分布,可以看出:叶轮进口区域及叶片吸力面附近区域气泡平均直径较大,蜗壳近壁区和蜗壳出口段内气泡平均直径较小,且与叶轮内相比,蜗壳流道内气泡平均直径较小;随着进口气体体积分数的增大,叶轮流道内气泡平均直径有所增大,蜗壳流道内气泡平均直径增大幅度较小,这可能是因为随着进口气体体积分数增大,气泡在叶轮流道内聚集形成气团,因此叶轮流道内气泡平均直径增大;蜗壳流道内的压力较高,而气泡间距较大,气泡尺寸增加程度较小,因此蜗壳流道内气泡平均直径增大幅度较小.

图5 设计工况下不同进口气体体积分数时泵内流道中间截面气泡平均直径
4 试验验证
4.1 扬程和效率验证
图6为设计工况下数值计算和试验得到的扬程和效率曲线对比,可以看出,当进口气体体积分数分别为0.5%,1.0%,1.5%,2.0%,2.5%和3.0%时,数值计算和试验的扬程相对误差分别为4.3%,3.9%,4.0%,3.0%,2.9%和3.0%,效率相对误差分别为4.9%,4.7%,3.7%,3.5%,3.2%和3.3%.计算值和试验值较接近,各工况下扬程和效率的相对误差都在5%以内,说明均一MUSIG模型可以较为准确地预测叶片泵的水力性能.

图6 数值计算和试验的性能曲线对比
4.2 气相分布验证
图7为设计工况下IGVF=1.0%时数值计算和高速摄影可视化试验得到的叶轮内气相分布,可以看出,数值计算和试验得到的叶轮内气相分布基本相符,气泡主要分布在叶片吸力面和流道中部区域;数值模拟的叶轮流道内气相体积分数相对试验较少.这主要是MUSIG模型设置的离散气泡尺寸范围不够大,组数不够多,与实际情况存在差异,所以模拟结果和试验会存在一些差异.总体上,数值模拟与试验拍摄图片比较吻合.

图7 数值计算和可视化试验的叶轮内气相分布对比
5 结 论
将以TFM模型为基础的MUSIG模型应用于叶片泵内气液两相流场数值计算,分析了压力分布、不同尺寸气泡分布和气泡平均直径分布等,并进行了试验验证,得到如下结论:
1) 随着入口气体体积分数增大,叶片压力面流道高压区面积逐渐减小,叶片吸力面气相聚集区和叶片吸力面尾迹区内气体体积分数增加,高气相体积分数区域面积扩大.
2) 叶片吸力面气相聚集区主要是大直径气泡,而叶片吸力面气相尾迹区、蜗壳近壁区和泵出口段主要为小直径气泡.
3) 随着入口气体体积分数的增大,泵内各处气泡平均直径都增大,叶片吸力面存在气泡平均直径较大的区域.
