新疆地区潜在蒸散量计算模型适用性评价

殷昌军，桂东伟*，刘云飞，张 磊，薛冬萍，刘 毅

（1.中国科学院 新疆生态与地理研究所 荒漠与绿洲生态国家重点实验室，乌鲁木齐830011；2.新疆策勒荒漠草地生态系统国家野外科学观测研究站，新疆 策勒848300；3.中国科学院大学，北京100049）

0 引 言

【研究意义】潜在蒸散量是区域水文循环和能量平衡中一个重要环节，是影响气候与环境变化的最重要因素之一[1-2]，在不同时空尺度能量和水文循环中发挥关键作用[3]。特别是在生态脆弱和对全球变化敏感的干旱地区[4]，各自然要素时空分布极不均匀，潜在蒸散量的准确计算对于该区域实际蒸散量的估算、干旱程度的评价和气候变化趋势的预测等方面具有重要意义[5-6]。

【研究进展】潜在蒸散量的计算方法较多，大体上按影响因素可以分为综合法、辐射法、质量传输法和温度法4 类[7-9]。以往针对干旱区潜在蒸散量的研究主要关注蒸发量在不同时空尺度上的变化[10-11]。然而，研究中所使用的蒸发计算模型并不是在每个地区都适用。其中最常用的就是将联合国粮农组织建议的Penman-Monteith（P-M）公式[13]的计算结果作为基准值与其他模型相比较[14-18]，并判断这些模型的适用性。但是Rosenberry 等[19]研究发现P-M 公式这类同时需要太阳辐射和空气温度的方法计算结果有时并不比基于空气温度的方法具有优势，并且基于温度的方法在某些研究区域更经济有效，计算结果也更精准。Majidi 等[20]在研究中发现，在使用月时间步长数据时，Makkink 等辐射-温度方法具有合理的精度。阴晓伟等[21]研究发现中国西北干旱区1964—2018年不同时期，潜在蒸散量受到不同气象因素的影响程度具有一定的区别。钟巧等[22]在对新疆博斯腾湖流域潜在蒸散量的归因分析时发现山区和平原地区的潜在蒸散量变化的主导因素存在差异。【切入点】由于不同地区影响潜在蒸散量的因素具有差异，不同模型对不同气象要素的敏感程度不同，在计算潜在蒸散量时需要选取适宜当地的模型以提高计算精度，不能简单地以P-M 公式计算结果作为潜在蒸散量的基准值，它在不同地区的适用性同样需要进行评价。特别是在新疆地区，由于相关研究较少，南北疆气候条件（如地表反射率、风速、水汽压和云量等）存在差异[23]，这些差异必然会导致同一潜在蒸散量估算方法在不同地区得到的蒸发量计算结果存在差异性[24-25]。【拟解决的关键问题】有必要验证估算方法的区域适用性，确保所选方法的计算结果能够较为精确地反映当地蒸发情况。

本研究利用新疆16 个气象站点1970—2015年的实测气象资料，采用不同方法计算各站历年逐月潜在蒸散量，对不同站点的潜在蒸散量的变化趋势进行分析，并以实测蒸发数据估算的潜在蒸散量为标准，使用随机森林模型对不同气象要素的权重进行分析，最后选取“逼近理想解的排序法”即TOPSIS 模型[26]，通过每种计算方法的相关性、精度、灵敏度指标对模型的适用性进行排序，提出适合于新疆不同区域的蒸发量计算模型。

1 研究区概况及数据资料

新疆地处东经 73°40′—96°18′ ， 北纬34°25′—48°10′之间，幅员辽阔，地形复杂，为明显的温带大陆性气候。天山横亘于新疆中部，将新疆分为南北两半，天山以北为北疆，天山以南为南疆。新疆气温温差大，降水量少，气候干燥，年平均降水量约为150 mm，但各地降水量相差很大，与北疆相比，南疆的气温更高、降水更少。

地区之间的气候差异巨大，因此潜在蒸散量在地区之间存在很大差异。本文选取在新疆均匀分布的16 个站点的气象数据进行研究分析，站点的分布如图1 所示，所使用的数据主要为1970—2015年的逐日实测气象数据。该数据来源于中国气象数据共享服务网（http://data.cma.cn）。其中潜在蒸散量标准值由各台站内E601B 型蒸发皿实测数据，结合前人研究得到的全国蒸发皿系数分布结果[27]计算得到。

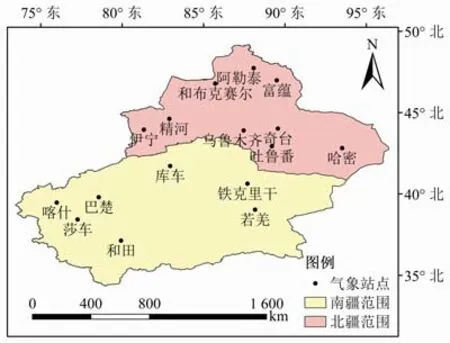
图1 新疆地区气象站点空间分布示意Fig.1 Spatial distribution of meteorological stations in Xinjiang

2 研究方法

2.1 蒸发计算方法

本文共使用了7 种潜在蒸散量估算方法，包括1种综合法（Penman-Monteith（P-M，简称）[28]）、3 种辐射法（Priestley-Taylor（P-T，简称）[29]、Hargreaves（Harg，简称）[30]、Makkink[31]）、1 种质量传输法（Penman[32]）以及2 种基于温度的估算方法（Hamon[9]、Mc Cloud（MC，简称）[33]）进行比较分析（表1）。

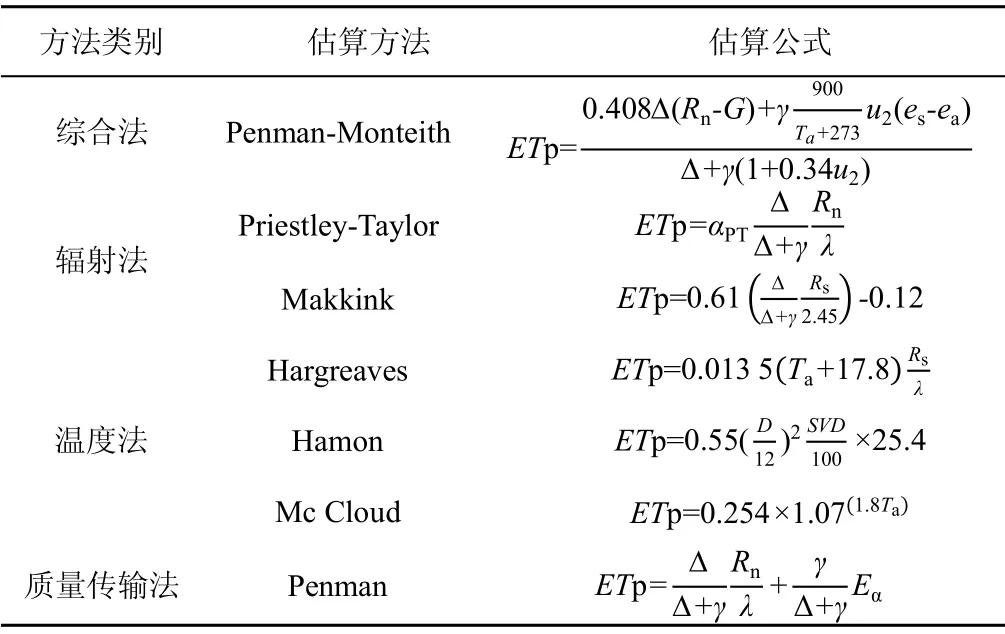
表1 潜在蒸散量估算方法Table 1 Methods of estimating potential evapotranspiration

表1 中ETp为潜在蒸散量（mm/d）（在后续公式中如若特殊说明，ETp单位均为此）；G为土壤热通量密度（MJ/（m2·d））；Rn为作物表面的净辐射（MJ/（m2·d））；γ为干湿计常数（kPa/℃）；Ta为2 m 高处的日平均气温（℃）；es为饱和水汽压（kPa）；ea为实际水汽压（kPa）；Δ为温度-饱和水气压关系曲线T处的斜率（kPa/℃）；u2为2 m 高处风速（m/s)；其中G值较小，在计算过程中忽略不计；αPT是经验系数，假设无平流的条件下Priestley-Taylor 推荐取1.26；λ为汽化潜热，取值2.45（MJ/kg）；Rs为短波辐射（MJ/（m2·d））；D为日照时间（h）；SVD为平均温度下的饱和水汽密度（g/m²)；Eα=（6.43（1+0.54u2（es-ea））/λ)；其余符号意义及单位与相应参考文献相同。

2.2 影响排序方法决策的指标基础

2.2.1 准确度指标

为了客观地评价分析结果，采用相关系数（r）、纳什效率系数（NSE）、均方根误差（RSME）和平均相对误差（MRE）4 种评价指标来评价7 种方法和实测数据的相关性、结果误差和模型质量，r越接近1，RMSE越小，MRE越接近于0，表明计算结果和标准结果差异越小，反之则差异越大。NSE取值为负无穷至1，NSE接近1，表示模型质量好，模型可信度高；NSE接近0，表示模拟结果接近观测值的平均值水平，即总体结果可信，但过程模拟误差大；NSE远远小于0，则模型是不可信的。

为了探究不同站点潜在蒸发量的主要影响因素，选择随机森林算法判断平均气温、最高气温、最低气温、相对湿度、风速和净辐射量对潜在蒸散量的影响程度。随机森林算法通过抽取多个不同的训练样本集和随机选取节点分类特征来增大分类模型之间的相异性，从而提高模型的泛化和预测能力，具有精度高和性能稳定的特点，可用来进行分类、拟合和预测。另外，随机森林还能计算指标的相对重要性，模型提供2 种参数重要性的评价指标，平均准确度下降值（Mean Decrease Accuracy）和Gini值（Mean Decrease Gini），2 种指标均为无量纲。本文选取平均准确度下降值作为参数重要性的评价指标，该指标的基本思想是把一个变量变为随机数后，观测随机森林预测准确性的降低程度，该值越大表示该变量的重要性越大。

2.2.2 敏感性指数

在通常情况下，数据和输入变量的不确定性通常是未知的[34]。每个蒸发公式都各自包含一组变量。这些变量的测量或多或少都会存在一定的误差，这些误差可能源于仪器校准不当、测量地点不合适、外部因素对测量装置的影响以及读取数值时的误差。每个蒸发公式都对所涉及的变量表现出敏感性。本文评估了蒸发公式对输入变量的敏感性，允许这些变量在其观测值的±10%范围内确定或随机变化[34]。

根据误差的来源和类型，设置了5 种情景来计算和分析模型的敏感性。第1 场景和第2 场景分别对模型的每个变量施加+10%或-10%的变化，而其他变量保持不变，以评估计算结果相对于受变化的变量的百分数的敏感性。第3 场景和第4 场景单独为模型的每个输入变量施加一个（0，+10%）或（-10%，0）范围的随机变化。第5 个场景则是对模型的每个变量施加1个（-10%，+10%）范围的随机变化。

每个模型的总灵敏度是针对不同情境下的每个变量计算的。将蒸发计算模型对应的5 种情景总灵敏度计算式为：

式中：Aij为第i种方法对灵敏度情景j的总灵敏度；M为样本总数；Yijk为第i种方法对其第k个变量的灵敏度，并与灵敏度情景j相对应。并非所有变量都存在于每种方法中，这意味着对于第i种方法中不存在的变量，其灵敏度为0。

2.3 适用性评价方法

TOPSIS 模型又称“逼近理想解的排序法”，是一种距离综合评价法。其原理为检测出评价对象与最优值、最劣值的加权欧式距离，再计算评价对象与理想值的贴近度，进行优劣排序。

实现TOPSIS 的步骤首先是创建一个判断矩阵V（式（2）），设有样本数为m，指标数为n：

第一步，数据标准化：由于不同指标的量纲可能不同，为使各指标具有可比性，需要对评价指标进行归一化处理，即标准化，得到决策矩阵Y：

第二步，确定指标权重，构建加权的决策矩阵：采用熵值法确定指标权重Wn，建立加权判断矩阵Z：

第三步，根据加权判断矩阵确定各指标的最优解和最劣解

第四步，计算各目标值与理想值之间的欧氏距离和

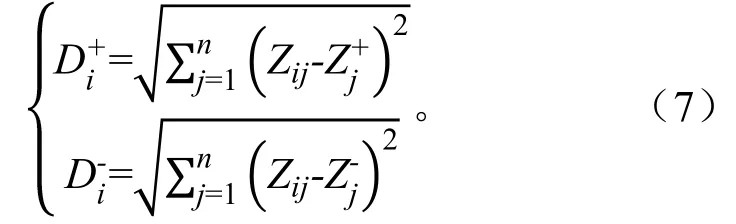
第五步，确定贴进度Ci：

Ci值越接近于1，证明该对象与理想值越靠近，即对象相对较优，最终按贴进度由大到小进行排序。

3 结果与分析

3.1 潜在蒸散量计算结果比较

7 种潜在蒸散量计算模型与标准值在所有站点计算的多年月均潜在蒸散量的变化过程如图2 所示。

从图2 可以看出，7 种估算方法得到的潜在蒸散量与标准值的多年月均值变化趋势基本一致，均表现为“夏季高，冬季低”的变化特征，最高值出现在7月，最低值出现在1月或12月。在大多数站点Makkink模型与P-M 模型的计算值与标准值最为接近，Hamon模型的计算值与其他方法相差最大。MC 模型的计算值则与其他模型的变化趋势最不一致，这可能是由于温度法仅将温度作为唯一考虑的气象因子有关。

图2 基准值与7 种模型计算ETp 的多年月均变化比较Fig.2 The comparison of multi-year average ETp by month estimated by benchmark value and other seven methods

为了进一步比较这些模型的计算结果与潜在蒸散量值的相似性与准确性，利用r、MRE、RSME与NSE对其进行误差分析，结果见表2。

从表2 可以看出，温度法（Hamon、MC）的计算结果与标准值的r在所有地区都为最小值，其中Hamon 模型的相关系数虽然较MC 方法略高，但是其NSE在所有站点都为负数，且远小于0，说明其在这些地区计算结果质量较差。与此同时，Hamon 与MC 模型的MRE和RSME都高于其他模型计算结果，说明这2 个模型质量较差，是不可信的；辐射法在所有站点的计算结果与蒸发皿估算值的相关系数均在0.94 以上，NSE都较接近于1，并且MRE和RSME在所有模型中也处于较低水平，说明辐射法整体计算结果较好，可信度较高；综合法P-M 模型与Penman模型相比，其各指标参数结果在所有站点都较为稳定，没有出现在某个站点与标准值的计算差异过大，说明P-M 模型在所有站点具有一定的广泛适用性，而Penman 模型计算得到的指标参数则在不同站点表现出明显的差异性，说明其具有明显的地区适用性。

结合图2、表2 可知，各站点的综合法P-M 模型计算结果与标准值的变化过程基本保持一致，NSE总体上在0.8 左右，但MRE较辐射法略高；质量传输法中的Penman 模型的r、MRE和NSE在所有模型中均处在中间水平，但变化过程与蒸发皿估算值吻合度不如辐射法和P-M 法；辐射法中的Makkink 模型计算结果与标准值的变化过程吻合度很高，r均在0.95以上，平均相对误差和均方根误差总体较低，整体估算质量要优于质量传输法和辐射法中的其他方法。

表2 基准值与7 种模型计算月ETp 的结果Table 2 Monthly ETp calculated by benchmark value and seven methods

综合来看，7 种估算方法中，辐射法整体估算精度优于其他方法，其中Makkink 模型计算精度最佳，综合法P-M 模型和标准值的相关性最好，Penman 模型精度次于辐射法和P-M 模型，温度法精度最差，辐射法中的Harg 模型与温度法相比，由于考虑了除温度以外的大气边缘太阳辐射，其计算结果相对较好。

3.2 潜在蒸散量影响因素分析

为了探究新疆不同地区潜在蒸散量的主要影响因素，本文使用随机森林模型，选取平均气温、最高气温、最低气温、相对湿度、风速和净辐射量的月均值作为输入值与潜在蒸散量的月均数据进行拟合，并通过平均准确度下降值判断各个要素对潜在蒸散量的影响程度，值越大说明对潜在蒸散量的影响越大。为避免随机森林模型出现过拟合，对各个参数进行了归一化处理。

不同气象因素对潜在蒸散量的影响结果如图3所示，影响新疆地区不同站点蒸发量的因素主要为净辐射量和气温，这一结果与前人的研究[21-23]相似，但南北疆有一定的差异，南疆潜在蒸散量的主要影响因素为平均气温、最低气温和净辐射量，北疆则主要为平均气温、最高气温和净辐射量，并且不同站点之间也略有差异。因此在新疆气象数据较为缺乏的区域可以选择基于辐射量和气温参数较为简单的模型进行计算，由于不同区域受到的影响具有一定的差异性，因此，新疆地区潜在蒸散量的计算应考虑模型对不同气象要素的敏感程度，选取更为准确的方法。

图3 不同气象因素对潜在蒸散量的影响程度Fig.3 Influence of different meteorological factors on potential evaporation

3.3 蒸发模型的适用性评价

在利用TOPSIS 模型进行适用性评价之前，除了上述不同方法的精度指标外，还需要计算不同地区，7 种估算方法在5 种情境下的总敏感性。

再依据表2 的精度指标与计算得到的5 种情景的总敏感性作为TOPSIS 排序法的评价指标，对不同地区不同计算方法进行适用性排序。不同模型的TOPSIS 法排名结果如表3 所示。

表3 不同地区不同计算方法的总体排名Table 3 Overall ranking of different calculation methods in different regions

从最终的结果上看，在北疆地区计算潜在蒸散量适用性最好的是辐射法，Penman 模型与P-M 模型次之；在南疆地区适用性最好的是辐射法中的Makkink模型和综合法P-M 模型，质量传输法的Penman 模型处于中间水平。2 个地区适用性最差的模型均为温度法中的2 个模型。

4 讨论

本文中所有模型的多年月均值计算结果之间虽然存在差异，但是总体趋势相近，均表现为“夏季高，冬季低”的趋势。同时通过随机森林模型对引起潜在蒸散量变化的主要因子进行判别后发现主要影响因子为净辐射、气温，其次为相对湿度，这些都与前人研究[11，35]相似。

TOPSIS 模型是潜在蒸散量计算模型比较评价中的一种新方法[26]，在排序过程中对原始数据进行了规范化处理，并能充分利用原始数据的信息，所以能够充分反映不同模型之间的差距，具有真实、直观、可靠的优点，而且对于样本资料没有特殊要求，使得应用更加方便广泛。其中综合法P-M 模型基于能量平衡和传质理论，在理论上是最合理的[36]，但是在本文中的适用性评价中却不是最佳的，甚至在北疆部分站点的计算中排名靠后，仅高于基于温度这一单一变量的模型。造成这一现象的原因可能是综合法模型较复杂，所涉及的参数的多样性和数据量大给潜在蒸散量估算带来了较高的敏感性。而且，与辐射法等方法相比，基于传质理论的模型的一个缺点是需要根据当地的实际蒸散量来确定校准的传质系数，而辐射法中只需要标准气象数据就可以进行计算[37]。因此，尽管综合法的精确度相对较好，但其在北疆地区排名较低，并且在不同地区的适用性差异较大，而辐射法在新疆地区的适用性整体上要好于其他方法。其他仅考虑温度的方法虽然适用性排名较差，但是考虑到他们的简便性，以及可以通过部分实测数据对模型参数进行矫正以提高精确度[19]，在部分数据难以获取的地区具有很高的成本效益。

5 结论

1）全疆范围内，综合法P-M 模型计算值与潜在蒸散量的月相关性最好，辐射法次之，温度法最差。辐射法整体计算结果较好，可信度高；综合法的P-M模型在所有站点的计算结果都较为稳定，具有一定的广泛适用性，而Penman 模型的计算结果在不同站点表现出明显的差异性，具有明显的地区适用性；温度法中的Hamon 和MC 模型计算结果最差。

2）新疆地区潜在蒸散量的主要影响因素为净辐射量和气温，在新疆气象数据较为缺乏的区域可以选择基于辐射量和气温参数的较为简单的模型进行计算。

3）在南疆地区，辐射法中的Makkink 模型与综合法P-M 模型适用性最好，P-T、Harg 等辐射法次之，温度法最不适用；在北疆地区，辐射法适用性最佳，Penman 模型和P-M 模型次之，温度法最不适用。