基于平均能耗并融合整车状态的续驶里程估算
2022-03-21王鹏翔王芸芳
舒 航,史 强,袁 凯,王鹏翔,王芸芳
(陕西汽车控股集团有限公司,西安 710200)
0 引言
电动汽车具有节能环保、综合使用成本低、驾驶品质好等一系列优势,普及率越来越高[1-2],但纯电动汽车的续驶里程短、能量补充速度慢,导致用户产生里程焦虑[3],限制了其推广普及。为解决此问题,一方面需要开发高能量密度的电池及其相应的快充技术[4];另一方面提供一个准确的续驶里程估算结果有助于用户进行行程规划,提升电动车用户使用感受,缓解焦虑情绪[5]。因此,续驶里程估算的准确性研究成为当下电动汽车发展的研究要点。
目前,关于续驶里程的研究无论是应用聚类法识别工况进行续驶里程估算[6-7],还是利用车辆运行积累的大数据进行组织分析得到剩余能量对行驶距离估计[8-9],方法多单纯集中在对车辆典型运行工况的研究,存在运行工况不能全覆盖的风险,也没能考虑车辆自身状态对续驶里程的影响,且计算量大,工程应用性不强。本研究通过累计计算、周期更新车辆平均能耗,并在此基础上增加载荷状态判断、辅机能耗及时反馈和末端SOC剩余能量修正等功能,对纯电动汽车续驶里程进行估算。通过离线仿真和实车试验,验证了其有效性和工程应用性。
1 续驶里程估算
本研究按照时间累积方法实时估算续驶里程,估算算法流程图如图1所示:
估算算法由平均能耗估算、电池剩余能量估算和续驶里程估算3部分组成。
(1)平均能耗估算。车辆处于不同载荷状态时,单位里程能耗差别较大。引入载荷判断功能,依据不同载荷选择相应单位里程能耗作为初始平均能耗,以此估算续驶里程初值;初始平均能耗更新周期对后续由累计计算得到的平均能耗的稳定性有很大影响,通过定义评价指标,运用统计分析的方法确定初始平均能耗更新周期;大功率辅机开闭对续驶里程影响显著[10],本研究在空调/暖风开闭时刻对平均能耗进行同步修正,将辅机开闭对续驶里程的影响及时反馈给用户。
(2)电池剩余能量估算。在末端SOC阶段,由于BMS对电池的过放保护,导致在末端SOC的剩余能量估算误差较大[11]。根据动力电池母线电流、电压信号,实时计算电池剩余能量。在末端SOC引入电池剩余能量修正算法,提高剩余能量估算精度。
(3)续驶里程估算。由车辆行驶工况,根据得到的平均能耗和电池剩余能量,实时更新续驶里程估算值。

图1 基于平均能耗的续驶里程实时估算流程图Fig.1 Flowchart of real time estimation of driving range based on average energy consumption
1.1 平均能耗估算
1.1.1 平均能耗初值确定
车辆上电后的续驶里程初值是用户关注点之一,特别是商用车使用过程载荷变化较大,平均能耗区别明显[12]。为了续驶里程估算初值的准确性,需要根据整车状态确定车辆平均能耗初值。本研究由车辆启动加速过程中获得的整车动力参数,运用能量守恒原理快速计算整车质量,判断载荷状态,选择相应的平均能耗作为初值,流程如图2所示。
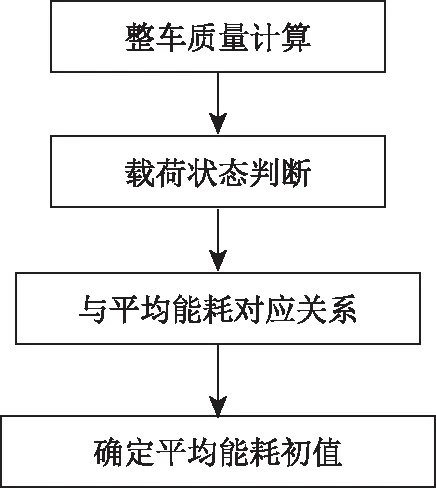
图2 平均能耗初值确定流程Fig.2 Process of determining initial value of average energy consumption
应用2种方法计算车辆起步过程用于驱动的能量:
(1)通过动力电池母线电压、电流计算,即
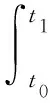
(1)
式中,E1为驱动车辆消耗的能量;Eo为车辆起步过程中附件能量消耗;ηS为电机的系统效率,与电机输出相关,即ηS=f(T,n),可以通过查询电机系统效率map得到;ηT为机械传动效率;uDC为直流母线电压;iDC为直流母线电流;t0,t1分别为加速过程的起止时间。
(2)通过电机输出的转矩、转速计算[13],即
(2)
式中,E2为驱动车辆消耗的能量;Ttq为电机输出转矩;n为电机转速。
考虑到车辆起步阶段,电机与电控的系统效率ηS较小且变化大,电机输出转矩亦不能真实测得,两种方法均存在一定的误差,所以通过权重系数w(0≤w≤1)将二者融合,减小能量E计算结果误差。对于信任度较高的计算方法可以给予其较高的权重系数。
E=w·E1+(1-w)·E2。
(3)
最后根据公式(4)计算整车质量,给出车辆的状态,输出相应的平均能耗初值,计算得到续驶里程初值。
(4)
式中,M为计算出的整车质量;v0为车辆加速过程初速度;vt为加速过程末速度。
应用上述方法,取权重系数w=0.4,利用某款轻型纯电动厢式物流车(车辆基本参数如表1所示)

表1 某轻型纯电动厢式物流车整车参数Tab.1 Parameters of a type of light-duty electric logistics van
在平坦道路的20次空载起步过程动力参数数据进行计算分析,结果如图3所示。计算得到的整车质量均在2 500 kg以下,平均相对误差为8.4%,计算结果相对集中,本研究将采用能量守恒法计算所得的整车质量作为车辆载荷状态判断输入。

图3 轻型纯电动厢式物流车整车质量计算结果分布Fig.3 Distribution of calculation results of mass of light-duty electric logistics van
本研究将上述轻型纯电动厢式物流车载荷划分为空载、半载和满载3种状态,分别对应的整车质量为2 500 kg以下、2 500~3 500 kg之间和3 500 kg 以上,通过计算出的整车质量所在区间来判定车辆相应的载荷状态。所提出的方法已在目标车型上针对不同载重、不同驾驶行为进行了超300次试验验证,载荷状态判断准确率达95%。
通过前期试验,获得车辆在3种载重下工况运行时的平均能耗,如表2所示。以此3种平均能耗分别作为空载、半载和满载状态下用于续驶里程估算的平均能耗初值,即可通过判断的车辆载荷状态来确定平均能耗初值。

表2 整车质量与平均能耗对应关系Tab.2 Correspondence between vehicle mass and average energy consumption
1.1.2 初始平均能耗更新周期确定
车辆上电起步短时间内车辆状态变化剧烈且数据量较少,计算得到的行驶平均能耗波动较大[14]。为了确定初始平均能耗更新周期T1大小,针对平均能耗以固定周期更新的计算方式,提出衡量周期平均能耗波动程度的指标δ,表征周期长度Tx与周期平均能耗波动之间的关系。将车辆行驶数据按不同时间周期Tx进行划分,计算周期平均能耗的波动性δ,计算方法为:
(5)
式中,n为划分的周期个数;eavg(i)为第i周期内行驶平均能耗;eavg_total为全程平均能耗;Tx为平均能耗更新周期长度;ttotal为车辆行驶总时长。
本研究借助积累的大量不同载重状态下轻型厢式物流车车辆城市工况行驶数据,通过统计分析来确定T1大小。得到图4所示波动程度与平均能耗更新周期长度变化关系,图中同一种符号代表一组工况行驶数据。

图4 平均能耗波动性与平均能耗更新周期长度关系Fig.4 relationship between volatility and update cycle length of average energy consumption
由图4可知,28组数据整体上随着周期时间长度增加,周期平均能耗波动越来越小,表明周期平均能耗与全程平均能耗逐渐接近。平均能耗更新周期超过1 800 s后波动程度集中在0.03以下、整体变化趋缓,因此,本研究取T1=1 800 s作为该车型平均能耗初值更新周期。
在设定初始更新周期T1内,平均能耗采用由载荷状态判断得到的初始值。上电时间超过T1后,通过累积的行驶里程和电池放电能量,计算得到行驶平均能耗作为下一周期续驶里程估算的依据,该过程中包含了车辆过去的行驶工况信息。平均能耗具体计算公式如(6):
(6)
式中,eavg为行驶平均能耗;Eout为累积电池放电能量;S为本次行程已行驶累积里程;eavgInit为行驶平均能耗值初值。
利用实车运行数据,进行离线仿真计算得到车辆某次工况运行eavg随时间变化情况,如图5所示。在T1=1 800 s的时间段内,由载荷判断得到eavgInit,该值与全程平均能耗0.19 (kW·h)/km吻合,说明载荷判断的有效性,可以确保续驶里程估算初值的准确性。在第1 800 s时平均能耗若直接由初值向累计计算值切换会有0.015 (kW·h)/km幅度的跳变,虽然整个过程平均能耗最大浮动为0.02 (kW·h)/km,1 800 s 处的跳变幅度尚可接受,但是会引起续驶里程估算结果的突变。因此在T1=1 800 s对平均能耗初值和累计计算值进行比较,若二者不等,则平均能耗则由初值线性向累计计算值过渡,过渡过程中当二者误差小于0.002 (kW·h)/km或者二者大小关系反向时,平均能耗随即采用累计计算值。另外,1 800 s 后平均能耗波动较小,说明初始平均能耗更新周期确定为1 800 s用于数据积累计算的合理性。
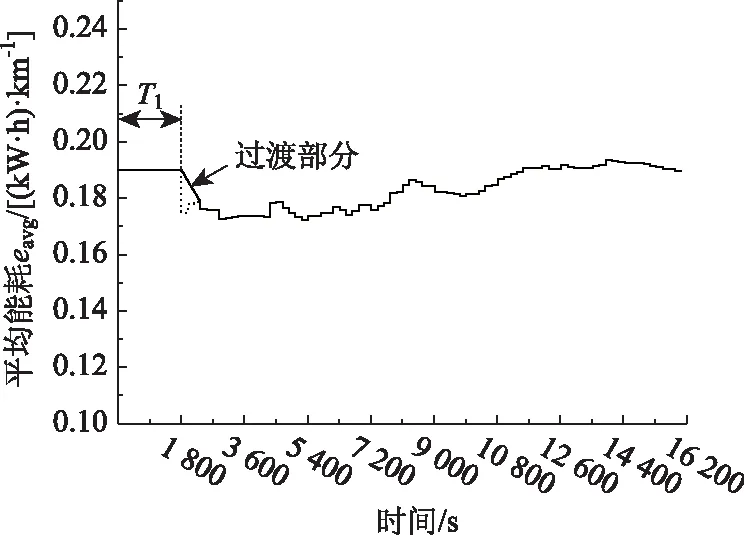
图5 整车平均能耗仿真计算Fig.5 Simulative calculation of vehicle average energy consumption
1.1.3 辅机能耗及时反馈
空调/暖风等大功率耗电辅机对纯电动汽车续驶里程有显著影响[15-16],为提高空调/暖风开闭时刻续驶里程估算结果的实时性,本研究考虑空调/暖风对续驶里程估算结果的影响,以空调为例进行说明。
当空调开启时,通过在eavg基础上增加空调平均能耗进行及时修正,保持ton_hold时间后,恢复到eavg。因为eavg本身是由Eout以及S计算得到,空调开启对eavg的影响会随着平均能耗周期更新逐渐体现;当空调关闭时,在eavg基础上减去eAC进行及时修正,保持toff_hold时间后恢复。通过以上方式确保平均能耗及时变化,增强驾乘人员的直观感受。计算过程如式(7)所示:
(7)
式中,Vehavg为平均能耗;g(t),h(t)分别为平均能耗修正时机调节函数;eAC为空调开闭时刻平均能耗修正量;tAC_on,tAC_off分别为空调开启和关闭时刻;PAC为空调功率;ton_hold,toff_hold分别为空调开启和关闭时平均能耗修正量保持时间;StAC_on,StAC_off分别为tAC_on和tAC_off对应车辆行驶里程;ε(t)为关于时间t的单位阶跃函数。
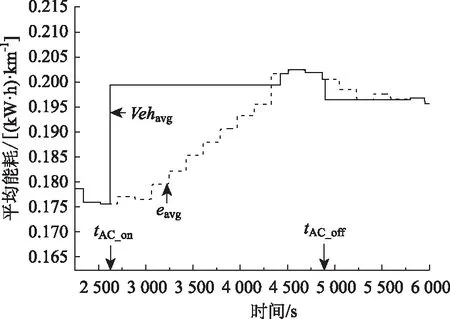
图6 空调开闭对车辆平均能耗的影响仿真Fig.6 Simulation of influence of on/off of air conditioning on average vehicle energy consumption
离线仿真得到空调开闭过程整车平均能耗变化过程如图6所示,仿真时取ton_hold=1 800 s,toff_hold=900 s。在空调开启瞬间整车平均能耗Vehavg由0.176上升到0.199 (kW·h)/km,1 800 s后平均能耗更新周期Vehavg与eavg保持一致,空调关闭瞬间平均能耗变化过程类似,与此同时反映到实时计算的续驶里程上,实现大功率辅机开闭瞬间对续驶里程影响的及时反馈。
1.2 电池剩余能量估算
动力电池在使用过程中,根据放电快慢可分为两大阶段:放电初期至中期,下降较慢,称为放电平台阶段;在放电末期,端电压急剧下降,称为放电末端阶段[17]。在放电末端阶段,由于SOC误差可能较大,BMS对电池的过充过放保护,导致在末端SOC的电池剩余能量估算误差较大,且因为续驶里程提前预警存在的问题[11],导致续驶里程估算误差较大,而该阶段的续驶里程正是驾驶员对充电时机判断的重要依据。
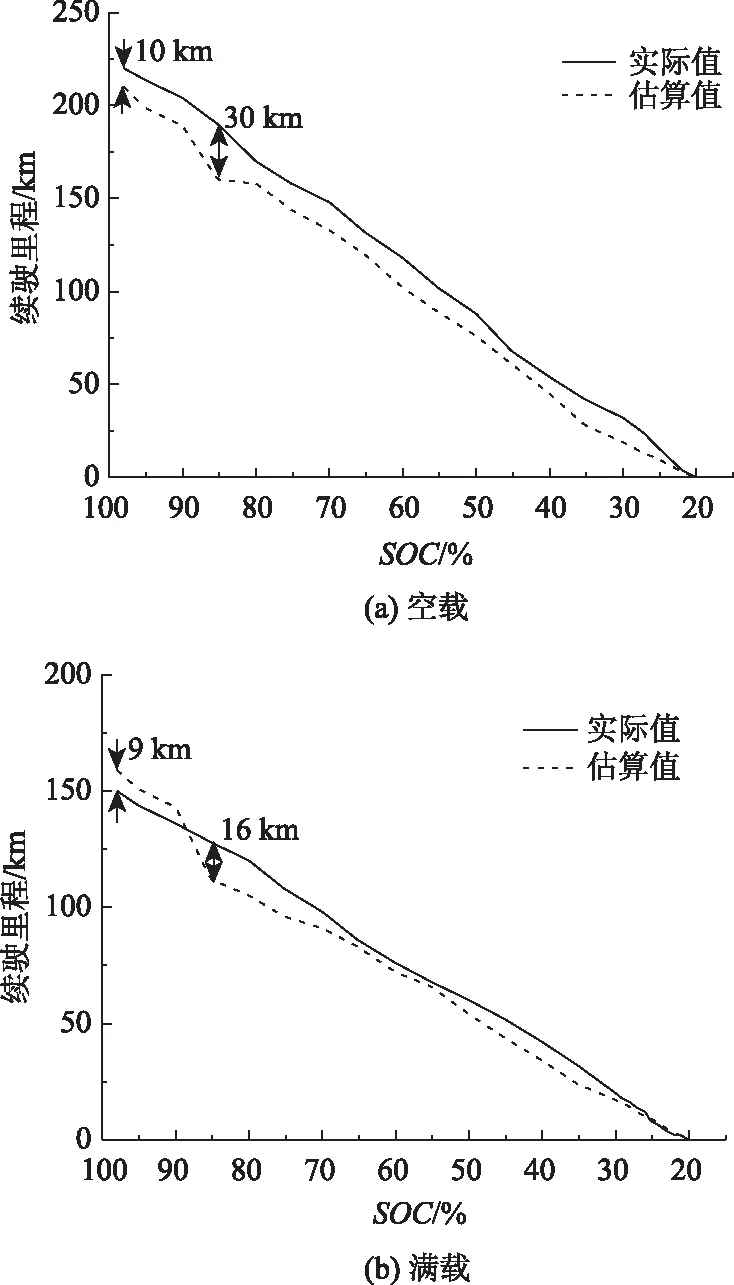
记录上电时SOC初值SOCInit,根据动力电池相关信号以及电能的流动路径[10,18],累积计算整车能量消耗Ereq,制动能量回收能量Erec,实时计算电池剩余能量BatAva。为提高末端SOC电池剩余能量的估算精度,设置末端SOC修正阈值SOCt,在SOClim (8) 图7 剩余能量修正前后仿真结果对比Fig.7 Comparison of simulation results of residual energy before and after correction 图8 修正前后续驶里程仿真值与实际值对比Fig.8 Comparison between simulation value and actual value of driving range before and after correction 式中,BatAva为电池剩余能量;Battotal为电池总能量;SOH为电池健康度;SOClim为放电截止SOC;Batdisabled为SOC=SOClim对应的电池剩余能量;BatSOCt为SOC=SOCt时的剩余能量。 本研究的试验车辆SOClim=20%,取修正阈值SOCt=30%进行仿真计算,对比修正前后末端SOC可用剩余能量以及续驶里程的变化情况。由图7可以看出,修正前的剩余能量估算值在SOC等于25%时已经为0,此时电池放电还未到达截止SOC,不符合实际情况;修正后的剩余能量估算更加精确,实时计算持续到截止SOC,和车辆实际行驶情况相一致。在图8中,末端SOC修正前的续驶里程仿真值与实际值误差较大,平均绝对误差在3.8 km左右;修正后的仿真值和实际值误差明显降低,平均绝对误差减小至1.7 km。 根据公式(7)得到的平均能耗与公式(8)得到的电池剩余能量,实时计算车辆续驶里程: (9) 式中VehRange为续驶里程。 为验证本研究所提续驶里程实时估算算法的有效性和准确性,建立续驶里程估算模型,根据上述厢式物流车空载和满载状态的城市运行工况数据对所提算法进行离线验证。 将车辆空载和满载运行数据输入模型进行仿真计算,续驶里程仿真值与实际值对比如图9所示。车辆空载状态时,仿真得到的续驶里程初值与实际值绝对误差为4.3 km,相对误差为2.4%;仿真值与实际值最大绝对误差为18.4 km,平均误差为5.2 km。满载状态时,仿真得到的续驶里程初值与实际值绝对误差为5.0 km,相对误差为3.3%;仿真值与实际值最大绝对误差为13.1 km,平均误差为3.2 km。 图9 车辆续驶里程实际值与仿真值对比Fig.9 Comparison of actual value and simulation value of vehicle driving range 以轻型纯电动厢式物流车为试验用车,对续驶里程估算算法进行实车测试验证。行驶路线为根据西安地区新能源物流车运营大数据构建[19]的西安典型行驶工况,其中之一的特点如图10所示,试验车辆工作循环数据统计特征如表3所示。试验过程中不开启空调暖风,驾驶员根据道路情况正常驾驶,初始平均能耗周期T1=1 800 s,电池电量从98%以上放电至截止SOC,试验车辆分别在空载、满载状态下进行试验。 图10 西安地区纯电动物流车典型行驶工况之一Fig.10 One of typical driving conditions of battery electric logistics vehicle in Xi’an 表3 纯电动物流车典型工作循环数据统计特征Tab.3 Statistical characteristics of typical work cycle data of battery electric logistics vehicle 车辆空载续驶里程实车试验结果如图11(a)所示,初始时刻续驶里程估计值与实际值绝对误差为10 km,相对误差为5.4%。全程估计值与实际值之间最大绝对误差为30 km,平均绝对误差为9.9 km。 车辆满载试验结果如图11(b)所示,初始时刻续驶里程估计值与实际值绝对误差为9 km,相对误差为6%。全程估计值与实际值最大绝对误差为16 km,平均绝对误差为5.3 km。 图11 车辆续驶里程实际值与估算值对比Fig.11 Comparison of actual value and estimated value of vehicle driving range 空载和满载试验结果充分表明本研究的续驶里程估算算法是有效的,并能保证一定的精度。 (1) 通过累积计算、周期更新车辆平均能耗,结合车辆载荷判断、辅机能耗及时反馈机制和末端SOC剩余能量修正等功能,实现对纯电动汽车续驶里程实时估算。 (2) 分别在车辆空载和满载状态进行离线仿真和实车验证,充分证明所加功能的合理性,及续驶里程实时估算算法的有效性和工程实用性,为纯电动汽车的续驶里程实时估算提供一个新方法。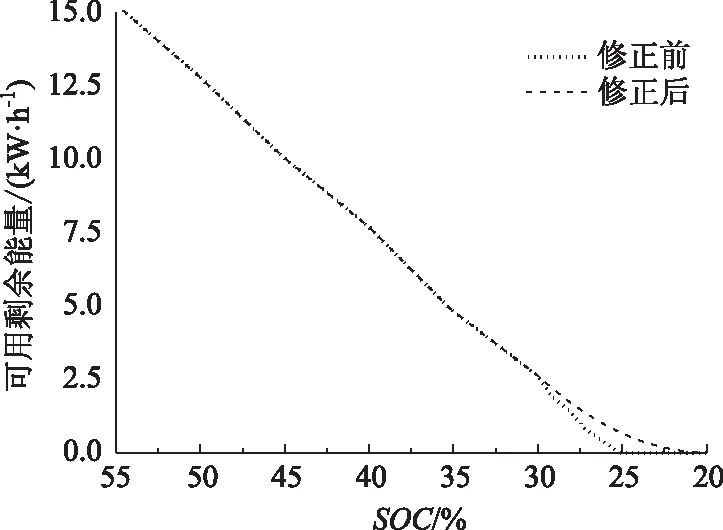

1.3 续驶里程估算

2 试验验证及结果分析


3 结论
