基于身管地磁感应场的弹丸炮口速度测量方法
2022-03-21王廉斌
王廉斌,李 凯,韩 焱
(中北大学信息探测与处理山西省重点实验室,山西 太原 030051)
0 引言
弹丸炮口速度是影响火炮射击精度和弹丸命中率的关键参数之一,对其实现精确测量具有十分重要的意义。
目前常用测量方法大致可分为外测法与内测法,其中外测法形式众多。雷达测速法较为成熟[1],美国的M90、俄国的UAABS等装置,均依据雷达测速原理。区截法的使用较为广泛,文献[2]设计了一种软件计时和FPGA控制相结合的双光幕测速系统,提高了测速准确性和灵活性。文献[3]提出一种X射线和光幕靶结合的方法,解决了火炮发射时炮口烟焰强烈等问题。文献[4]设计了一套基于ARM和FPGA利用网靶测量弹丸速度的系统,结构简单、成本较低。文献[5]将两线圈装在炮口处,利用弹丸飞过线圈造成的磁场扰动测来测量弹丸初速,适合高炮发射弹丸。文献[6]根据红外线信号对炮口高炮射弹的遮挡效应,利用红外区截法可完成炮口后效区弹丸初速测量,可靠性较高。还有一些其他方法,文献[7]使用高速摄影系统测出弹丸速度,精度高,但易受天气等限制。
内侧法多为弹载传感器形式。文献[8]等利用电子测压器得到火炮膛底压力曲线,推出弹底压力后,积分解算出炮口速度,方法具有创新性。文献[9]利用线圈式传感器产生的感应电动势中所携带的弹丸角速度信息,测出了炮口角速度,结合炮口缠度计算出了弹丸炮口速度。文献[10—11]陆续对该方法进行了深入研究,使得弹载磁传感器法的实用性得到了进一步验证和发展。
目前对于炮口速度测量的研究较多,但外测法不能实现弹丸自主智能化调控;弹载内测法往往需要通过测量其他参数间接解算出速度,无法直接测量,过程较为复杂。针对上述问题,本文提出基于身管地磁感应场的弹丸炮口速度测量方法。
1 身管地磁感应场分布理论
一般火炮身管铁磁性材料的相对磁导率μr≫1,故其磁阻远小于空气磁阻。因此当火炮处于地磁环境中时,不论外部地磁场为何种方向,身管材料都会对其产生屏蔽效应,膛内磁场变小,当地磁场为某方向时屏蔽现象如图1所示。
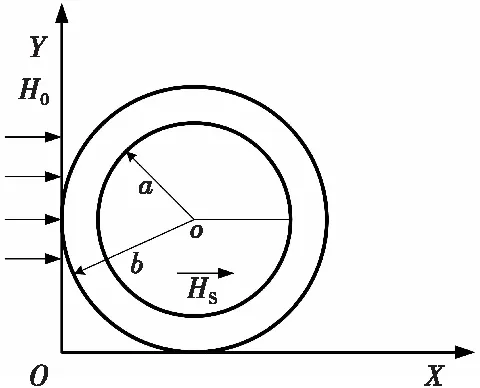
图1 身管磁屏蔽示意Fig.1 Body tube magnetic shielding schematic
屏蔽效果可由式(1)表示[12]:
(1)
式(1)中,H0为外部磁场强度,Hs为膛内磁场强度,a和b分别为火炮的内、外半径。
出炮口后,磁场屏蔽作用消失,但炮口附近存在边缘聚磁效应,其磁力线分布如图2所示[13]。
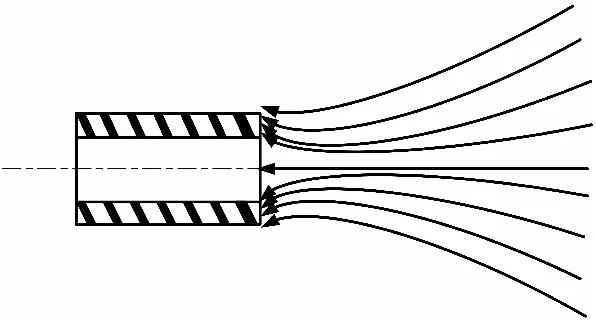
图2 炮口磁力线分布示意图Fig.2 Schematic diagram of the muzzle magnetic field line distribution
由上文分析可知,当火炮处于地磁环境中时,由于身管铁磁性材料和炮口结构突变的影响,导致身管不同位置磁场分布不同,产生了独特的地磁感应场。在此基础上,弹丸又常为导磁材料,因此在其发射过程中会对身管磁场造成扰动。这些扰动信息与弹丸运动过程密切相关,通过在弹丸上设置磁感应传感器获取扰动后的磁场信息,可实现弹丸运动参数的测量。
2 弹丸炮口速度测量方法
2.1 身管磁场分布特征仿真分析
为了研究利用地磁信息进行弹丸运动参数测量的可行性,本文首先对身管磁场分布进行仿真。由理论分析可知地磁场在火炮系统中存在磁屏蔽和边缘聚磁现象,利用COMSOL软件对身管内有无弹丸情形分别进行仿真。


图3 施加地磁场Fig.3 Applied geomagnetic field
2.1.1无弹丸情况磁感应强度仿真
1) 沿径向磁感应强度分布
当膛内没有弹丸时,沿身管径向的某条直线路径上磁场表现如图4所示。由仿真结果看出,径向上环境地磁场的磁感应强度约为2.1×104nT。由于身管为铁磁材料,磁场在身管壁中聚集,磁感应强度增强了约两个数量级,达到了约1.1×106nT。而通过身管壁进入膛内后,因为磁屏蔽作用,磁场减小了近3个数量级,约为3.7×103nT,为外部环境磁场的17%。
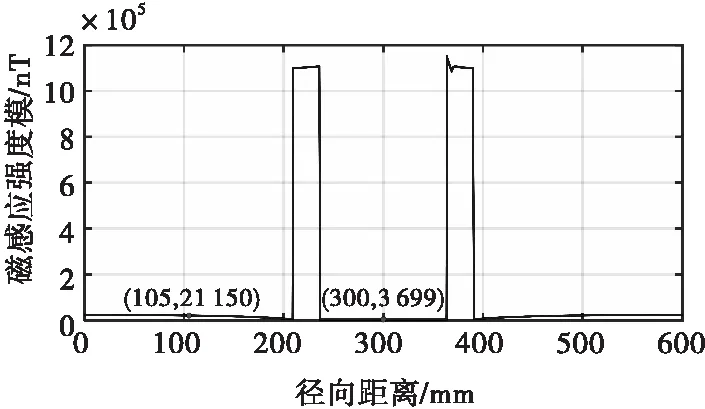
图4 沿径向路径磁感应强度分布Fig.4 Magnetic induction intensity distribution along the radial path
2) 沿轴向磁感应强度分布
沿身管中心轴线方向磁感应强度分布如图5所示。由仿真结果看出,膛内磁感应强度很小,最大值在3.7×103nT左右,接近平稳,约为此时外部环境地磁场5.4×104nT的7%。接近炮口时,磁屏蔽作用减小,身管的聚磁作用突显,在150 mm的距离内磁感应强度达到了约7.76×104nT,约为所施加地磁场的1.4倍。经过约500 mm的距离,趋于地磁场大小。由此可见,在炮口附近磁感应强度发生了剧烈变化。
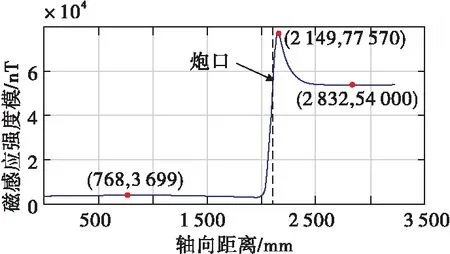
图5 沿轴向路径磁感应强度分布Fig.5 Magnetic induction intensity distribution along the axial path
2.1.2有弹丸情况磁感应强度仿真
在已有身管模型的基础上,设置弹丸模型,高度为660 mm,弹丸壁厚15 mm,底端存在两条弹带,如图6所示。将弹带材料设为铜,弹丸壁材料的相对磁导率设为300,引信材料的相对磁导率设为1。对弹丸模型在身管中运动到中某一位置时的情况进行仿真。
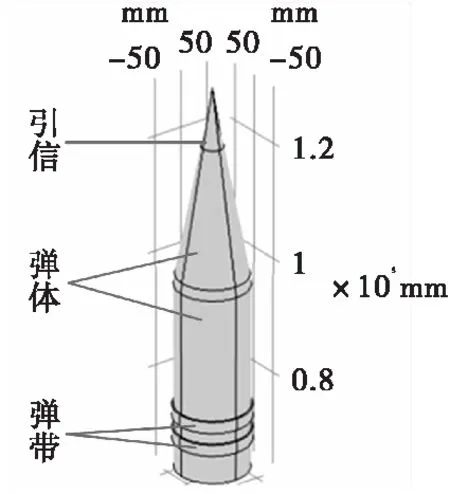
图6 弹丸模型Fig.6 Projectile model
1) 沿径向磁感应强度分布
在弹丸锥体形状处取一条沿身管径向的直线路径,其上磁感应强度分布如图7所示。由仿真结果看出,身管外部环境磁场和身管壁中磁场与无弹丸时大小几乎一致。区别在于进入膛内后,身管壁与弹丸锥体壁之间的空气中磁感应强度明显增大,在1.5×104nT左右,约为无弹丸时膛内空气磁感应强度的4倍,这是由于弹丸材料的铁磁性质导致膛内也产生了聚磁效应。之后磁场在弹丸壁材料中聚集,磁场又增大。通过弹丸壁材料进入弹丸内部后,由于身管壁和弹丸壁的双重屏蔽作用,磁感应强度迅速下降到8.6×102nT左右,数值极小。

图7 弹丸在膛内某一位置时径向磁感应强度分布Fig.7 Radial magnetic induction intensity distribution when the projectile is at a certain position in the bore
2) 沿轴向磁感应强度分布
沿身管中心轴线方向磁感应强度分布如图8所示。由仿真结果,易得到弹丸具体位置。膛内起始部分磁场在3.6×103nT左右;遇到弹丸时,磁场在弹底材料中聚集,增强了约两个数量级;通过弹底材料进入弹体内部后,磁场被双重屏蔽;到弹丸头部时,又产生一次较小的聚磁效应;通过弹头后进入膛内空气中,直到炮口,该段磁场分布与无弹丸时表现基本一致。
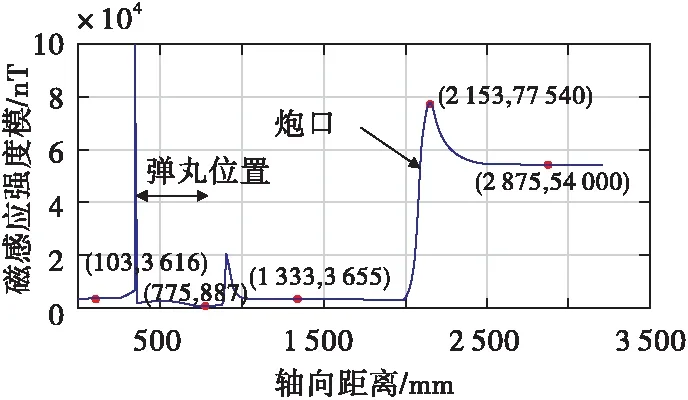
图8 弹丸在膛内某一位置时轴向磁感应强度分布Fig.8 Axial magnetic induction intensity distribution when the projectile is at a certain position in the bore
由图8可知,弹丸在膛内运动到某一位置时,会对无弹丸时中心轴线方向上磁场产生极大影响。弹丸发射是动态过程,其从膛内运动到膛外,图中弹丸位置标注的磁场趋势有无数个,即整条路径上磁场都会发生变化。
2.2 弹丸运动过程中磁场分布
由2.1可知,弹丸运动到某一位置,则运动路径上该位置附近磁场会发生变化,取弹丸头部刚到炮口、弹丸出膛一部分、弹丸完全出膛瞬间三个位置进行仿真研究,结果如图9所示。由图9(a)可看出,膛内弹丸颜色不明显,其磁场较小;由图9(b)可看出,弹丸出膛一部分后,除引信外的出膛部分磁感应强度变大,未出膛的部分磁场仍较小;由图9(c)可看出,弹丸全部出膛后,除引信和弹带外,弹体其他部分整体磁感应强度变大。且图9(a)、(b)、(c)中身管磁场分布也有所区别,故空气中磁场受弹丸和身管壁影响亦有差别。这表明,弹丸运动到不同位置,会使得整体模型的磁场分布产生不同程度的变化。
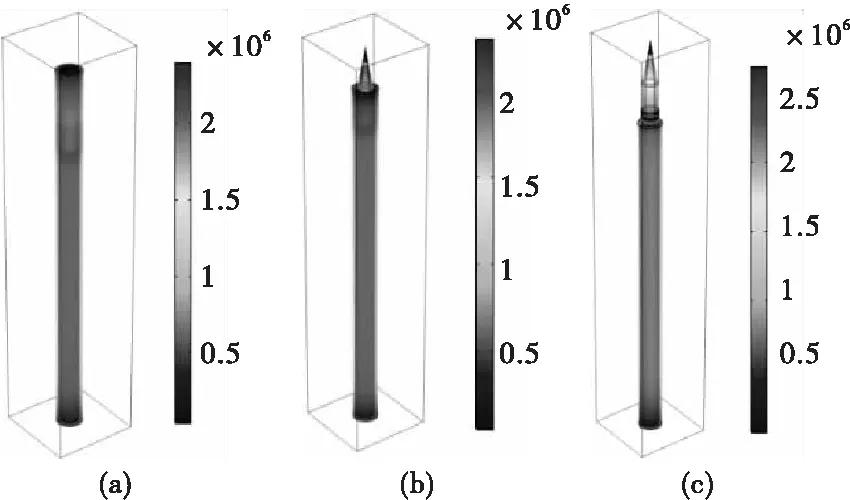
图9 磁感应强度模分布云图Fig.9 Magnetic induction intensity distribution cloud map
由图9可知,弹丸从膛内飞出过程中不同时刻模型的磁场不同,本文假设磁传感器位于引信表面,与身管壁距离为26 mm,对弹丸运动过程中其感知磁场进行仿真。
选择弹丸从膛内发射到膛外过程中的50个位置进行仿真,分别得到对应每个位置处传感器对应磁感应强度值,使用MATLAB中的Smoothing Spline函数对其进行光滑拟合,获得弹丸飞行过程中该路径上近似磁场分布,结果如图10所示。图中圆点为各个位置对应的磁感应强度值,曲线为光滑拟合曲线。由图10可知,由于受弹丸影响,有弹丸时磁感应强度值为无弹丸时的2~4倍。炮口处磁场在约400 mm的距离内增加到1.7×105nT,且在200 mm内磁场接近稳定状态,这与无弹丸时曲线特征差别极大,最大值并不是只有一个峰值。经过约100 mm的距离下降到约1.55×105nT,之后逐渐趋于稳定,磁场保持在约1.53×105nT。稳定后的磁感应强度值几乎为所施加地磁场的3倍左右,此时弹丸已经完全出膛,这表明即使弹丸已经离开炮口一段距离,但其本身的聚磁效应仍旧增强了该路径上磁场。
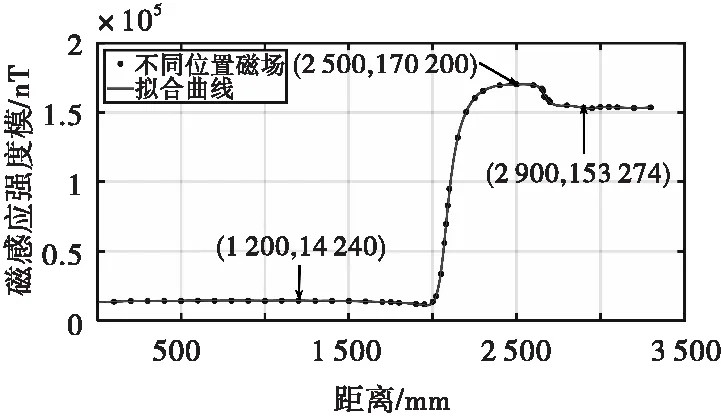
图10 弹丸运动过程中磁场变化趋势Fig.10 Trend of magnetic field during projectile motion
由图10可看出,弹丸运动过程中,整条路径上磁感应强度都得到增强。但膛内和炮口的磁场波动幅度则存在较大差别,远离炮口的膛内磁场波动比较平稳。炮口附近急速上升过程的磁场变化约为1.6×105nT,下降到稳定过程的磁场变化约为1.5×104nT,数值较大。故存在利用炮口附近的磁场变化来进行速度测量的可能性。
2.3 不同射向和射角下炮口速度测量方法
接下来需进一步研究炮口附近的磁场特征,但2.2节中磁场规律仅为图3情况下的分布。不同型号的火炮射角有所不同,例如中国W1968年式122 mm榴弹炮的射角为-7°~+22°,且射向也不固定,这导致火炮射击方向与地磁矢量的夹角不为定值,变化范围较大。因此,对两者夹角进行设置,仿真0°、33°、45°、57°、60°、70°、80°、90°下炮口附近磁场分布,对比结果如图11所示。图中3条黑色竖线分别标注了弹丸头部开始出膛、传感器出膛和弹丸完全出膛的位置,后图同样如此标注,不再赘述。
由仿真结果可知,随着身管射击方向与地磁矢量夹角增大,磁场上升和下降部分趋势逐渐不明显。因此易知:当磁场方向完全与射击方向平行或在身管方向上的平行分量较大时,磁感应强度值较大,上升和下降规律明显,完全平行时曲线趋势表现最好;与之相反,当磁场完全与射击方向垂直或平行分量较小时,磁场下降趋势较差,完全垂直即90°时,下降趋势最差。
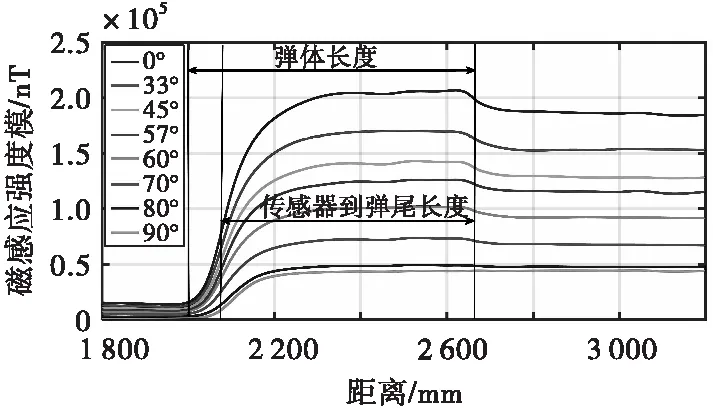
图11 炮口附近磁场拟合曲线对比Fig.11 Comparison of the fitted curves of the magnetic field near the gun port
特此说明,当射向射角改变时,两者夹角可能会出现钝角等情况。为方便说明,假设地磁矢量方向改变,大小不变,分别为70°、110°、250°、290°,射向不变,如图12所示。这四个角度的地磁矢量在射击方向和与射击方向垂直的方向上分量大小相同,则其磁感应强度大小曲线也相同,因此认为四种情况下两者夹角一致,故为避免重复,上文图11不绘制90°之后的角度。
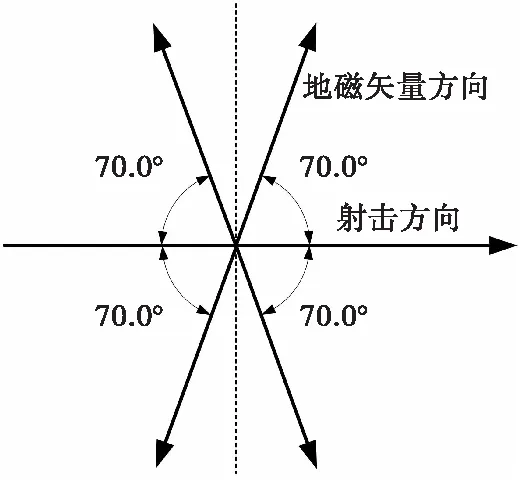
图12 夹角角度Fig.12 Angle of clamping
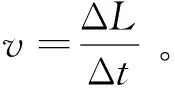
本方法利用炮口处随弹丸运动导致的磁场的急剧变化特征,测量该变化过程,实现测速。其中借鉴了弹载磁传感器法[9-11]的传感器安装方式和区截法[2-6]的测量原理,但与弹载法相比,本方法可实现直接测量,无需得到其他参数后间接解算炮口速度;与区截法相比,本方法依据磁场在运动路径上的变化规律获取特征点得到固定距离,无需在炮口安装区截装置。
3 仿真分析及验证
3.1 特征点确定及验证
为更准确地分析磁场变化特征,验证上文方法,对图11中所有曲线求一阶导函数,结果如图13所示。
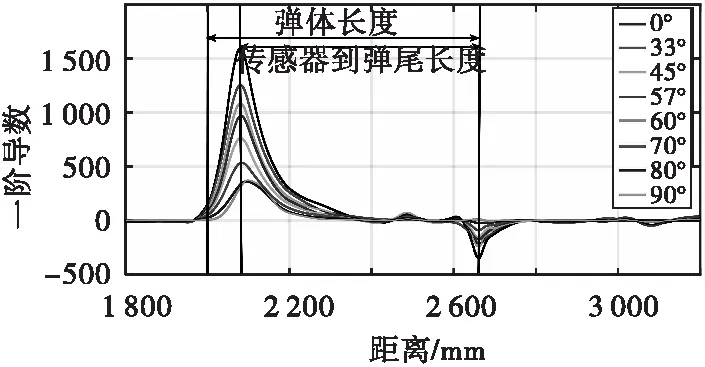
图13 一阶导函数曲线对比Fig.13 Comparison of first-order derivative function curves
由图13可看出,在第一条黑色竖线之前,膛内磁场变化率极小,接近于0。当磁场方向与身管射击方向完全平行或平行分量较大时,曲线整体数值偏大,且存在如下规律:在弹丸头部开始出膛时,磁场变化率快速增大,在传感器出膛时变化率达到一个正向峰值。之后变化率开始减小,当弹丸接近完全出膛时,开始出现负的变化率,到完全出膛时达到一个负的峰值。之后变化率增加,逐渐趋于稳定,接近于零。
将传感器出膛点和弹丸完全出膛点设为特征点,两个峰值处位置分别命名为lmax和lmin。
当磁场方向逐渐趋于与身管方向垂直时,曲线值较小,且正峰值逐渐向第一个特征点右侧偏移,负峰值越来越小,逐渐趋于0。
夹角小于等于70°时,正峰值几乎与第一个特征点重合,负峰值与第二个特征点重合;大于70°时,正峰值向第一个特征点右侧偏移,负峰值极小。此时两峰值间距离正好对应于两特征点间距离,即传感器安装位置到弹尾的长度,L0=lmax-lmin。
为了得到特征点更多信息,对图11中曲线进行二阶求导,结果如图14所示。同上文结论一致,当磁场方向与身管射击方向完全平行或平行分量较大时,可看出,二阶导函数曲线在两个特征点处正好为过零点,且在特征点两侧曲线变化幅值较大;当磁场逐渐趋于与身管方向垂直时,过零点逐渐向第一个特征点右侧偏移,第二个特征点处所有曲线都近似过零,但特征点两侧幅值变化极小,不到1。
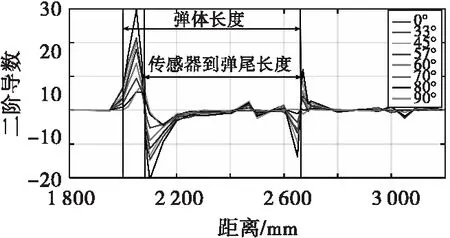
图14 二阶导函数曲线对比Fig.14 Comparison of second order derivative function curves
从图上数值观察,当夹角70°时,负峰值约为-3.3,已经很小,故测量时两者夹角最好保持小于70°。但不必过于在意这一点,实际测量中,即使火炮射向射角改变,也几乎不可能出现两者夹角近似或完全垂直的情况。
从上述炮口磁场变化特征分析可看出,当地磁方向与射击方向夹角小于70°时,弹丸在炮口附近的磁场变化具有显著的信号特征,即传感器出膛和弹丸完全出膛会产生磁场的变化率极值点;且两点都为磁场分布曲线二阶导数的过零点,即拐点。基于上述特征即可实现对弹丸炮口速度的测量。假设弹丸由lmax到lmin的运动时间为t0,则弹丸的炮口速度近似为:
(2)
图15为测量示意图。对该过程进行分析,假设测量系统对传感器信号的采样速度为Δt,在某时刻Δti=ti-ti-1信号采样期间的弹丸位移Δli=li-li-1,磁感应强度变化为ΔBi=|Bi-Bi-1|,传感器输出信号为ΔVi=Vi-Vi-1,每次对采集到的信号进行判别是否为最大值,检测到ΔVi为最大值,计数器开始计数,当检测到最小值时,停止计数。假设计数器最终输出为N,则t0=N·Δt,则根据式(2)可计算得到炮口速度。图16为测量流程图。
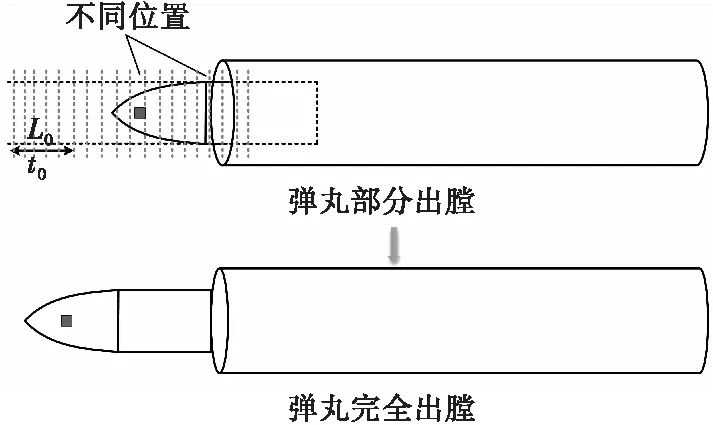
图15 测量示意图Fig.15 Measurement diagram
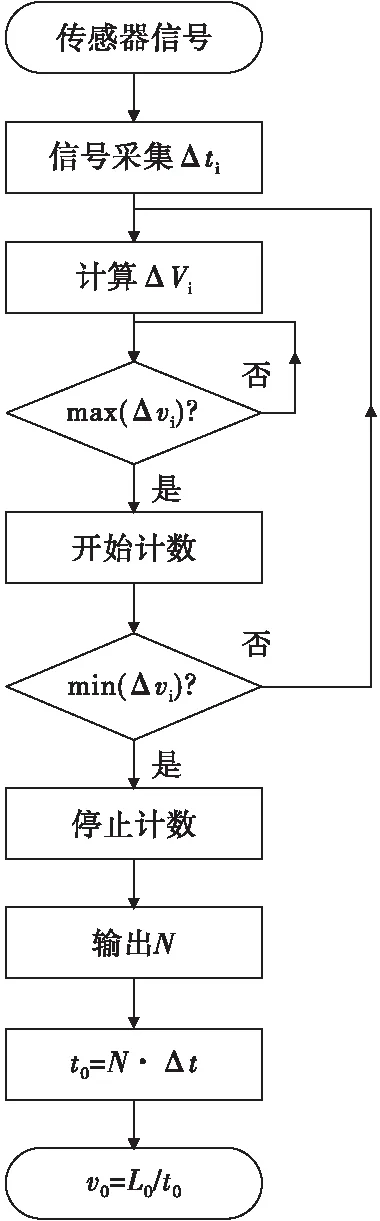
图16 测量流程图Fig.16 Measurement flow chart
3.2 测量影响因素分析
3.2.1干扰因素分析
弹丸运动过程中,除地磁场外,存在很多干扰因素,主要有[15]:1)火药气体电离形成的等离子体运动导致出现复杂电磁场,这是弹药发射复杂电磁环境的主要来源,对出炮口阶段影响极大;2)仪器、电子设备产生的电磁波等。两种干扰相较于几乎稳定的地磁场频率较高,对地磁检测系统影响有限,采集到信号后可进行高频滤波等相关手段得到地磁信号。
3.2.2测量可行性分析
本文方法既有优点,又存在一定局限性:1)根据本文测量原理,由距离除以时间得到速度,不再必须测得转速后间接获取速度,使得弹载测速法可用于非高旋弹种;2)由前人研究[13,16],可得炮口附近磁场变化近似符合本文所述趋势,但实测时存在弹丸,弹丸对炮口曲线的影响需要高精度传感器才可测得。
4 结论
本文提出基于身管地磁感应场的弹丸炮口速度测量方法。该方法通过有限元仿真,得到弹丸运动过程中炮口磁场幅值变化明显,且其导函数曲线中两特征点对应距离固定的分布特征,根据两点间距离除以磁传感器对应运动时间可实现炮口速度测量。仿真实验结果表明,当地磁矢量方向与射击方向夹角小于70°时,特征点极易识别,理论上可实现炮口速度的直接测量,为今后进一步的实际测试提供了参考。
