微惯性接电开关载荷识别机构设计中的能量分析法

黄 巍，聂伟荣，席占稳，曹 云

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

微机电系统(micro electro mechanical systems，MEMS)因其功耗低、尺寸小、易集成、可批量生产等优点在工业生产中得到了迅速发展，在汽车、消费电子、航天航空、生物医疗、智能通信等行业领域得到了广泛的应用[1-2]。微惯性开关又被称作微加速度开关、微阈值加速度计，是基于MEMS工艺技术加工、集传感器与执行器于一体的微惯性器件，通常情况下其处于断开状态，只有在外部施加的加速度载荷超过特定值(阈值)时才会闭合并接通电路[3]。发展日益完善的微惯性开关，因MEMS技术的独特优势而逐渐应用在汽车安全、智能穿戴和武器准备等领域中[4-6]。

针对某些特定应用场景使用的微惯性开关，如应用于引信电源系统的微惯性接电开关(以下简称为接电开关)，除了要能够稳定导通以外，为防止运输或其他勤务处理时因意外跌落导致出现安全问题，还应具备发射载荷和勤务跌落载荷的载荷识别功能，保证在勤务跌落环境下接电开关不会闭合而在发射环境下可以正常闭合。为实现这一功能，研究者们在接电开关中加入了载荷识别机构。文献[7]基于曲折槽式后坐保险机构分析并设计了相应的环境识别机构，然而该种类型的机构由于层间结合力较小，导致其在高过载下容易出现分层脱离现象。文献[8—9]设计了抗高过载性能更为优秀的齿形结构。文献[8]仅从位移响应上对机构的特征参数进行了分析与设计，没有从工作原理上进行阐述和分析；文献[9]将载荷识别机构等效为一阻尼常数，结果表明整体位移响应曲线更加匹配，然而这一等效阻尼模型无法描述单次碰撞过程，亦无法描述机构特征参数的影响。本文在文献[9]的基础上，针对原有设计方法中存在的局限性，提出一种能量分析法，这种方法从载荷识别机构的工作原理进行分析，并且能够更好地描述单次碰撞过程，从而描述特征参数对机构的影响，可以作为辅助设计方法。

1 载荷识别机构工作原理

1.1 接电开关工作原理

载荷识别机构为接电开关的一部分，要想解释机构的工作原理需要先分析接电开关的工作原理。开关物理模型如图1所示，为两个质量-弹簧-阻尼系统的串联系统。质量块m1、弹簧k1和阻尼c1组成环境响应模块，用以感受外部加速度并产生质量块m1的位移响应y(t)；锁头m2、弹簧k2、阻尼c2和闭锁梁则组成接电模块，这一部分为开关的电极部分，用以和外部电路连接。质量块m1在惯性力作用下运动到与锁头m2相碰后，推动锁头m2一起运动，锁头m2撑开闭锁梁并继续向前运动一段位移后，发生弹性回落并在闭锁梁限制下形成闭锁，实现电路的稳定接通。

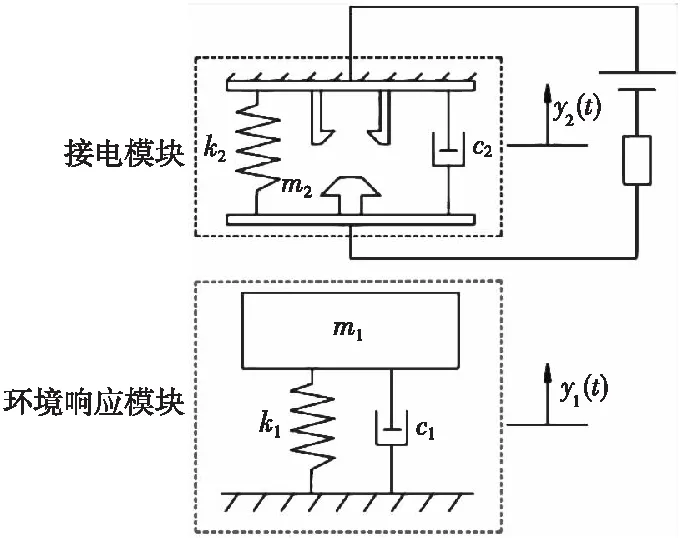
图1 微惯性接电开关物理模型示意图Fig.1 Schematic diagram of physical model of micro-inertial power switch

1.2 载荷识别机构结构分析

载荷识别机构为图2所示的齿形机构，作用于环境响应机构。单齿的特征参数包括齿形角β、齿高H和重合度γ，其决定了单齿的结构。该机构包括多组齿对，其中附加在质量块m1上的齿作为主动齿对，附加在两侧固定杆上的齿为被动齿对。质量块m1在外部载荷的作用下向敏感方向运动，在运动过程期间主动齿与被动齿发生碰撞，从而发生能量损失，在不同类型载荷下能量损失存在差异，进而实现载荷的识别。

图2 齿形载荷识别机构示意图Fig.2 Schematic diagram of teeth damping mechanism

2 能量分析法

能量分析法从系统能量得失角度去研究问题。在环境响应系统的运动过程中，能量来源为惯性力所做的正功，而能量损耗主要为齿与齿之间的碰撞(与接电模块接触前)。以下分别从惯性力正功和碰撞动能损失两方面介绍能量分析法。为便于分析，以两种典型载荷：幅值8 000g、脉宽2 ms的发射载荷(以下简称载荷1)和幅值15 000g、脉宽100 μs的勤务跌落载荷(以下简称载荷2)为研究对象。

2.1 惯性力正功

环境响应模块的能量来源是惯性力所做正功，即惯性力在质量块m1达到最大位移前做的功，可由式(1)求得：

(1)

式(1)中，tr为环境响应模块达到最大位移的时间，F是惯性力，v是环境响应模块的速度。以上值均可通过以下各式求得[9]：

F(t)=ma0sinω0t

(2)

(3)

(4)

图3 惯性力对环境响应模块所做正功Fig.3 Positive work done by inertia force to environmental response module

2.2 碰撞动能损失

(5)

式(5)中，vy为碰撞物体的屈服临界速度，是一个与物体材料属性、表面形貌等相关的参数。由式(5)可以得到物体的动能变化：

(6)

由式(6)可知，当碰撞物体结构和材料属性确定时，其动能变化量只与碰撞初速度vi相关，其变化曲线如图4所示，动能损失随碰撞初速度vi增大而增大。故而可以通过分析质量块m1在两种载荷下的碰撞初速度来判断其产生的动能损失差异。

图4 动能损失与初速度之间的关系Fig.4 The relationship between kinetic energy loss and initial velocity

设载荷1作用下质量块m1的速度为v1，碰撞动能损失为ΔE1；载荷2作用下质量块m1的速度为v2，碰撞动能损失为ΔE2。由式(3)、式(4)计算得到的不同位移和固有频率下的v1和v2如图5所示。可以看出，相同位移、相同固有频率下v1始终小于v2，即ΔE1<ΔE2。

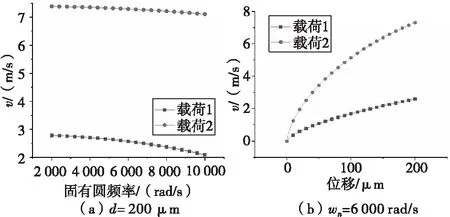
图5 质量块m1速度的变化曲线Fig.5 The variation curve of m1 velocity of mass block

综上所述，对于环境响应模块固有圆频率小于8 500 rad/s的接电开关，均满足ΔE1<ΔE2(相同位移下)和W1>W2的条件，通过设计合理的齿形载荷识别机构特征参数，即可实现对载荷1和载荷2的识别，且应可以实现对具有不同幅值、脉宽的两种载荷的识别，即具有普适性。

3 仿真分析

3.1 基于能量分析法的齿形特征参数分析

应用能量分析法，对载荷识别机构特征参数进行能量分析，并结合工艺要求提出对特征参数选取的要求。载荷识别机构通过影响环境响应模块运动过程中的动能损失工作，对惯性力正功影响较小，故以下只分析各特征参数对动能损失的影响。表1列出了接电开关的相关参数，作为仿真计算的基础数据。

表1 微惯性接电开关相关参数Tab.1 Parameters of micro inertia power switch

齿形角对动能损失的影响如图6(a)所示。系统的动能损失量和动能损失变化率均随着齿形角的增大而减小。齿形角是比较敏感的结构参数，应尽量减小加工误差带来的影响，因此齿形角应优先选择钝角；并且考虑到过大的齿形角参数会导致整体机构在敏感方向上的尺寸较大，因此应综合考虑影响后选择一个折中值。

动能损失与齿高的关系如图6(b)所示。齿高对动能损失的影响不大，只有非常小的波动。这是由于齿高的改变并没有改变碰撞的接触面积，整体上看对动能损失几乎没有影响。齿高决定了齿形的基本大小，齿高过大会导致整体尺寸过大，而齿高过小则不宜于加工。因此在这一参数对性能影响较小的情况下，应取一个中间数值。

重合度γ是指一组齿之间齿顶的相对间隙。通过计算得到的不同速度下动能损失与重合度的关系如图6(c)所示。由图所示，重合度对系统动能损失的影响整体上是线性的。这是由于重合度对齿与齿之间的接触面积的影响是线性的，而接触面积对摩擦力做功的影响也是线性的，所以重合度对动能损失的影响也是线性的。重合度是一组齿对之间的重要参数，在工艺加工中也是最容易出现较大加工误差的参数。由于过大的重合度会增大加工误差的影响，所以重合度应控制在较小的数值。

图6 各齿形结构参数对动能损失的影响Fig.6 Effect of tooth structural parameters on kinetic energy loss

通过上述单齿特征参数能量分析，结合工艺要求，确定单齿特征参数为：齿形角125°，齿高32 μm，重合度4 μm。由于多次碰撞是一个连续过程，因此需要对整体过程的能量得失进行分析。以下针对幅值8 000g、脉宽2 ms的发射载荷(载荷1)和幅值15 000g、脉宽100 μs的勤务跌落载荷(载荷2)，对载荷识别机构的齿数比进行能量分析。同理，主要对碰撞动能损失进行分析。

通过仿真计算得到在不同齿数比的齿形载荷识别机构作用下的质量块m1的动能损失曲线如图7所示。设载荷1下的动能损失为ΔE1m，载荷2下的动能损失为ΔE2m。图7(a)表示了不同齿数比下ΔE1m和ΔE2m的变化情况，在同一齿数比下，ΔE1m始终小于ΔE2m，这与之前的分析是一致的。图7(b)显示了不同齿数比下动能损失比ΔE1m/ΔE2m的变化，理论上这一值越小，质量块m1在两种典型载荷下由于齿形载荷识别机构产生的碰撞动能损失差异越大，载荷识别效果越好。然而这一数值来看，1∶2的齿数比应该具有最好的载荷识别效果，但是无法说明载荷识别的可靠性，故要结合位移响应分析进一步分析。

图7 不同齿数比下质量块m1的动能损失Fig.7 Kinetic energy loss of massm1 under different teeth number ratio

设质量块m1与齿形载荷识别机构作用后的最大位移分别为y1max(载荷1作用)和y2max(载荷2作用)。图8为不同齿数比下y1max和y2max比较的柱状图，其中各基准线为在各个齿数比下质量块m1上主动齿全部通过固定杆被动齿的最小位移，为实现可靠区分，y1max应大于这一值而y2max应小于这一值。(由于固定杆本身体积对质量块存在阻挡作用，使其后续运动受到限制，所以其最大位移只有1.26 mm。)由图8可知，当齿数比为1∶2时未能实现可靠载荷识别，故单从能量方面无法验证载荷识别的可靠性，需要结合位移响应进行分析。而单从位移响应方面无法得到最优的特征参数，当齿数比为2∶3、3∶2、3∶3时均可实现可靠的载荷识别，而通过能量分析，即可从这些备选参数中选择最优值，即动能损失比最小的2∶3。

图8 不同齿数比下质量块m1的最大位移Fig.8 The maximum displacement of mass m1 under different teeth number ratio

3.2 基于能量分析法的载荷识别普适性分析

设发射载荷的幅值为A1，脉宽为T1；勤务跌落载荷的幅值为A2，脉宽为T2。通常情况下，A1在1 000～30 000g之间，T1在2～8 ms之间；A2在8 000～15 000g之间，T2在100～300 μs之间[12-13]。以下基于能量设计法，对载荷识别机构的适用性进行计算分析，验证其能否适用于不同幅值、脉宽的发射载荷和勤务跌落载荷的载荷识别。设定基础参数初始碰撞距离为200 μm，环境响应模块的固有圆频率为1 000 rad/s。

图9为惯性力所做正功W1和W2分别随T1和T2变化的关系曲线。由图9可知，W1随T1增大基本呈上升趋势，当T1≈5 ms时达到最高点，之后又减小；W2随T2增大而增大，当T2=300 μs时达到最大值。除A1=1 000g外，W1的曲线基本均在W2的上方，对于大部分载荷均满足W1>W2。

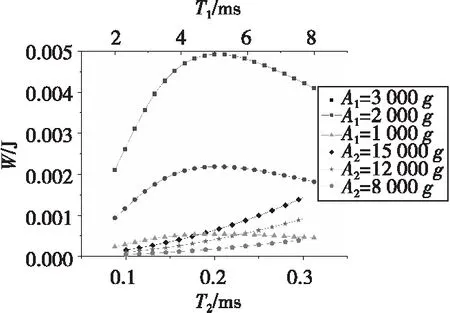
图9 不同载荷下惯性力所做正功Fig.9 Positive work done by inertia force under different loads

图10为相同位移下质量块m1的速度v1和v2分别随T1和T2变化的关系曲线。图10中，v1随T1增大先短暂增大，当T1≈3 ms时达到最高点，之后则减小；v2随T2增大而减小，当T2=300 μs时达到最小值。可以看出，v1始终小于v2，即碰撞动能损失ΔE1始终小于ΔE2。

图10 不同载荷下质量块m1碰撞初速度Fig.10 Collision velocity of mass m1 under different loads

综上所述，通过设计不同的齿形载荷识别机构的特征参数(齿形角、尺高、重合度、齿数比等)，可实现对不同幅值、脉宽的两种类型载荷的载荷识别，即齿形载荷识别机构对于载荷识别具有普适性。

4 结论

本文提出微惯性接电开关载荷识别机构设计的能量分析法，该方法基于载荷识别机构的工作原理，通过不同类型载荷下碰撞的能量损失的差异来实现载荷识别，从开关系统的能量得失角度，即惯性力正功和碰撞动能损失两方面对开关对于发射载荷和勤务跌落载荷的识别能力进行分析。仿真验证结果表明，可以更好地描述单次碰撞过程并且在载荷识别机构的设计中，该方法可以作为辅助设计方法以得到设计参数的优选值，并且基于此方法对载荷识别机构的适用性进行了分析，结果表明该机构具有普适性。