基于角点移位的三维地质断层快速建模算法

刘少华，吕瑞龙，伍东

1.长江大学地球科学学院，湖北 武汉 430100 2.中国石油集团工程技术研究院有限公司信息中心， 北京 102206

计算机相关技术的发展，使得如今能够通过三维建模的方式，为地下复杂的地质构造建立对应的实体模型，并提供可视化方法，这不仅能够大大提高非专业用户对于地质知识的认识与理解能力[1]，而且还为地质学家等的研究提供了一种新的方式。断层是在地壳中分布极为广泛的地质构造类型，断层活动影响着地层的沉积与剥蚀，控制着凹陷的形成和演化[2]，不仅影响着油气藏的形成与分布，还对油气开发、剩余油的分布具有重要的影响，因此构造清晰准确的断层模型对油气田勘探开发人员更准确地进行油气藏评价及开发管理有着重要意义。

对三维地质模型及地质断层模型的问题，国内外已进行了较为广泛的研究。在三维地质建模时，主要通过使用钻孔数据对地层模型进行插值，在插值算法方面，CHEN等[3]对深度变化时剪切波速度的变化进行研究，结合钻孔数据，使用克里金插值算法构建了苏州城区的三维地质模型；ARFAOUI等[4]等研究了克里格算子在研究地区重力面预测方面的优势; GONCALVES等[5]对地质结构隐式建模的机器学习算法进行了探讨。目前，国内外对于三维断层建模的方式主要分为整体法和局部法。整体法是先得到无断层的三维地质模型，再在此基础上根据断层数据生成包含断层的三维地质模型，适用于断层断距较小、断层数量较少的地质体；局部法是基于分区插值的方法生成断层模型，适用于断层数据较多、断距较大的地质体。三维地质模型的建模方式主要有表面数据模型、体元数据模型、混合结构数据模型，其中体元数据模型主要有三棱柱、四面体和六面体网格模型等[6]。表面数据模型建模所需数据量小，因此建模速度较快，但在表达地质体内部属性方面不如体元模型[7]，针对体元模型的剖切是当前断层模型构建的热点研究内容[8]。SADEGH等[9]分析了地震测量地质构造的相关参数，刻画了研究区的地层及地层的断裂情况；LIU等[10]采用VC++结合OPENGL，构建了一个地质建模的平台，通过研究地层的断裂等对矿区的塌陷进行预测；马钧霆等[11]采用剖切广义三棱柱生成多个四面体的方法，提出了对广义三棱柱的剖切算法；王海起等[12]采用垂向剖切的方式对六面体网格模型进行剖切生成剖切面，效率较高，然而不能生成斜剖面；张文东等[13]采用了分层投影求交点的方法解决六面体网格求剖切面的问题，需要多次判断是否相交并标记每一行的剖切六面体元的位置，实际剖切过程中会耗费较多资源；李定林等[14]利用三角网中三角网格的空间拓扑关系提高了获取三角网格的效率，但是在大数据量网格的情况下，维护三角网格的拓扑关系需要花费较多的时间，影响剖切效率；李昌领等[15]使用切割三棱柱生成多面体，再将多面体转化为多个四面体，在进行建模时需要进行多种数据结构的转换，较为复杂；张适[16]基于面元对地层进行建模，对地层模型剖切后会产生空洞，还需对空洞进行缝合。成熟的商业软件中，Petrel使用最优的基于阶梯化网格封堵性分析算法，RMS使用非阶梯化网格算法，控制条件繁杂，建模流程繁琐，适用于复杂断层建模。笔者提出一种基于角点移位的断层快速建模算法，基于整体法[17]思路，先不考虑断层对地层进行建模，计算断层面剖切的角点网格单元，将这些角点网格的角点按照一定方法移至断层面上，实现角点自适应断层模型。算法的优点在于维护了数据结构的完整性和体元个数的不变性，从而提高建模效率及稳定性。

1 建模流程

基于整体法的三维断层模型构建需要先构造不含断层的三维地质模型，再根据断层数据对三维地质模型进行修改，恢复地质体发生断裂的真实状态。生成断层模型算法主要流程如下：

1)使用分层数据进行地层划分，对目标地层生成六面体角点网格，根据层位点使用反距离加权插值算法计算六面体网格点的高程数据，构建不含断层的地质模型；

2)融入断层数据，对断层数据进行计算处理，生成断层上盘的顶面和底面、下盘的顶面和底面的断层线；

3)将三维地质模型沿断层线划分为上盘和下盘，对其进行分区插值；

4)根据断层线计算断层在三维地质模型中的位置，对断层线经过的六面体单元角点进行移位，完成对包含断层的地质体三维模型的构建。

2 地层模型构建

2.1 模型介绍

该研究基于六面体元结构生成三维地层模模型。每个体元由8个角点组成，根据建模范围、六面体的长、宽设置六面体元8个角点的X、Y方向坐标，高程坐标需要根据钻孔的层位数据，使用插值算法对每个六面体元的角点进行插值，适用的插值算法主要有克里金算法、反距离加权插值算法等。反距离加权插值算法具有很好的普适性，对断裂起伏地层的刻画更为明显[18]。可以通过设置六面体元的长、宽、层数，来控制建模范围内的六面体元个数，长、宽越小，层数越多，生成的三维地层模型中单位体积内体元数量越多，构建的模型就越精细。

2.2 模型构建流程

1)首先确定建模范围、六面体网格中每个六面体元的长(X方向步长)和宽(Y方向步长)，以及建模的层数；

2)确定建模的目标地层；

3)对目标地层构建六面体网格，根据建模范围及在X方向、Y方向的步长确定每个六面体元角点的X、Y方向坐标。

4)使用钻孔顶层控制点对当前层的所有六面体网格的顶面角点进行插值计算，使用底层控制点对六面体网格底面角点进行插值计算。

5)遍历所有目标地层，重复步骤3)和4)，即可完成模型构建。

3 断层数据及计算

3.1 断层数据说明

1)控制点。所需控制点为断层上盘顶面断层线上的已知点的三维空间坐标，且控制点个数应不少于2个。使用前2个控制点计算断层线在XOY平面投影线的直线方程，后续的点仅用来作为分区插值时的控制点。

2)断层倾角。断层面与六面体网格顶面的二面角。

3)层厚。断层处地层的厚度。

4)地层断距。断层上下两盘对应位置的垂直距离，上盘上升为正，下盘上升为负。

3.2 计算公式

对于一个地层模型来说，不含断层时只用考虑地层的顶、底2个面，包含断层时断层将地层断裂为上盘和下盘2个部分，因此断层模型就需要考虑上盘的顶面和底面、下盘的顶面和底面共4个面，导入的断层线数据中的控制点为上盘顶面断层线上的点，因此还需要根据断层倾角、层厚、断距来计算控制点在其余各面的对应点坐标。

若A(x1，y1，z1)、B(x2，y2，z2)为断层上盘顶面断层线上的2个点，层厚为h1，断层倾角为θ，断层断距为h2，则A点在其他各面对应点(说明：如果A点位于上盘的顶面时，则要计算的是上盘底面、下盘的顶面和底面对应的点)的三维坐标P(x，y，z)计算公式如式(1)～(3)所示：

(1)

(2)

z=z1-h

(3)

式中:h为各面对应点与上盘顶面控制点在垂直方向的距离，当计算上盘底面时，A点与上盘底面对应点在垂直方向上距离为地层厚度，即h=h1；当计算下盘顶面时，A点与下盘顶面对应点在垂直方向上距离为断距，即h=h2；当计算下盘底面时，A点与下盘底面对应点在垂直方向上距离为层厚加断距，即h=h1+h2。

4 断层入网

断层入网即在三维地质模型的顶面和底面上，断层线相交于网格线，把断层线经过的六面体元角点修改为相应的断层线与网格线的交点，把断层线作为断层上盘和下盘的边界，最后再对网格角点进行插值计算，得出移位后角点的高程值，插值时考虑断距及层厚数据，即可将断层的上盘与下盘分裂开来，从而实现模拟地层的断裂。在不考虑断层线平行于坐标轴的情况下，将断层入网问题分为逐行剖切和逐列剖切2种形式。

4.1 逐行剖切

将地层模型和断层线垂直投影至XOY平面，如图1(a)所示的断层线位置，即在每一行上，断层线切割六面体网格顶面不超过2个六面体元，此时断层线在XOY平面的投影直线斜率k∈(-∞，-K)∪(K，+∞)(K为六面体元宽与长之比，下同)。

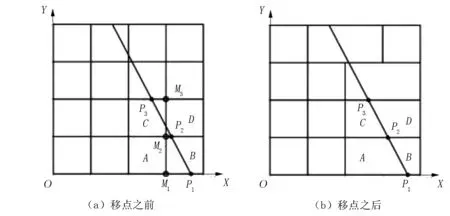
图1 断层线入网(逐行剖切)Fig.1 Fault line into the network (line by line division)

以六面体网格顶面为例，将六面体网格投影至XOY平面上得到如图1(a)所示四边形网格，逐行剖切方式算法步骤如下：

1)从四边形网格的第1行(沿Y轴正方向)开始，计算断层线m与该行网格的上下2个交点P1、P2；

2)如果相交单元格是该行最后一个，如图1(a)中单元格B，则将单元格B的左角点M1、M2分别移至交点P1、P2，由于相邻单元格角点不共用，因此需将单元格A的右角点M1、M2分别移至P1、P2；如果相交单元格不是该行最后一个，如图1(a)中单元格C，则将单元格C的右角点M2、M3分别移至P2、P3，将单元格D的左角点M2、M3分别移至P2、P3，移点效果如图1(b)所示；

3)重复步骤1)、2)，直至对模型最后一行进行移点；

4)按断层线将地层模型分区，对网格所有角点进行分区插值，完成断层建模。

计算六面体元网格中第i行被断层线剖切的六面体元的列号Ir的计算公式如式(4)所示：

(4)

式中：a、b、c为断层线方程ax+by+c=0的系数；Δx为六面体元在X轴方向的长度；Δy为六面体元在Y轴方向的长度；i为该行在六面体网格的行号。

4.2 逐列剖切

将地层模型和断层线投影至XOY平面，如图2(a)所示断层线位置，即在每一列上，断层线切割六面体元不超过2个，此时断层线在XOY平面的投影直线斜率k∈[-K，0)∪(0，K]。逐列剖切算法思路与逐行剖切相同，区别只是对六面体网格逐列进行分析，具体流程在此不进行赘述。

计算六面体元网格中第j列被断层线剖切的单元格索引Ic的计算公式如式(5)所示：

(5)

图2 断层线入网(逐列剖切)Fig.2 Fault line into the network (column by column division)

图3 断层位置的特殊情形Fig.3 Special case of fault location

式中:j为该列在六面体网格的索引。

式(4)和式(5)组成了快速判定断层线与六面体元网格相交的计算模型，加快了定位相交六面体元的速度，大大提高了断层入网的速度。

特殊地，针对断层线位于地质模型一角的情况，为了保证六面体元结构的统一性及六面体元个数的不变性，防止模型超出建模范围，将如图3(a)所示顶面为ABCD的六面体元N顶面的左角点A、B进行修改，将A点坐标修改为断层线与线段AB的交点坐标，由于断层线与线段DC所在直线交点位于建模范围之外，因此将D点坐标修改为C点坐标，然后修改六面体元N同行的上一个六面体元M顶面的右侧两点坐标为修改后的A、D两点坐标。如图3(b)所示为断层线位于一角时移点完成后效果图，此时整个六面体元网格中，六面体元个数保持不变，且六面体元结构仍为8个顶点(六面体元N顶面的C、D点重合)。

5 算法应用

使用所提出的算法对包含断层的地层进行三维建模，算法应用的计算机环境为：①操作系统：Windows 7 旗舰版 64位；②CPU规格： CPU @2.50GHz；③内存：金士顿 4G。算法应用选择了A工区12口井的钻井数据，建模地层有一条断层穿过。经测试，当网格大小设置为71m×90m×1层时，网格数量有7396个(网格角点数量59168)，建模时间为1650ms。而文献[13]对于六面体元的剖切，当数据点个数58275时，模型剖切时间为5684ms，在网格数量相等情况下，笔者所提出的算法效率比其高3倍。如图4所示为对2个地层进行三维断层建模的前后对比效果图，其中地质模型建模设置为横向范围为6040m，纵向范围为7680m，网格大小设置为120m×120m×1层。

6 结论

笔者提出了一种基于整体法的三维地质模型可视化表达方法，对含断层的地层进行快速建模，该算法通过对断层数据进行处理，判断断层面剖切六面体网格的剖切类型，设计了断层表达数学模型以计算断层线在断层上、下盘的顶面和底面上的位置，提出了快速判定断层线与六面体元网格相交计算模型，从而快速解算出逐行或逐列方向上，断层线相交六面体元的索引，并对六面体元的角点进行移位，从而使得模型表达更符合地层断裂的真实状态。对于单断层建模，该算法具有以下优势：

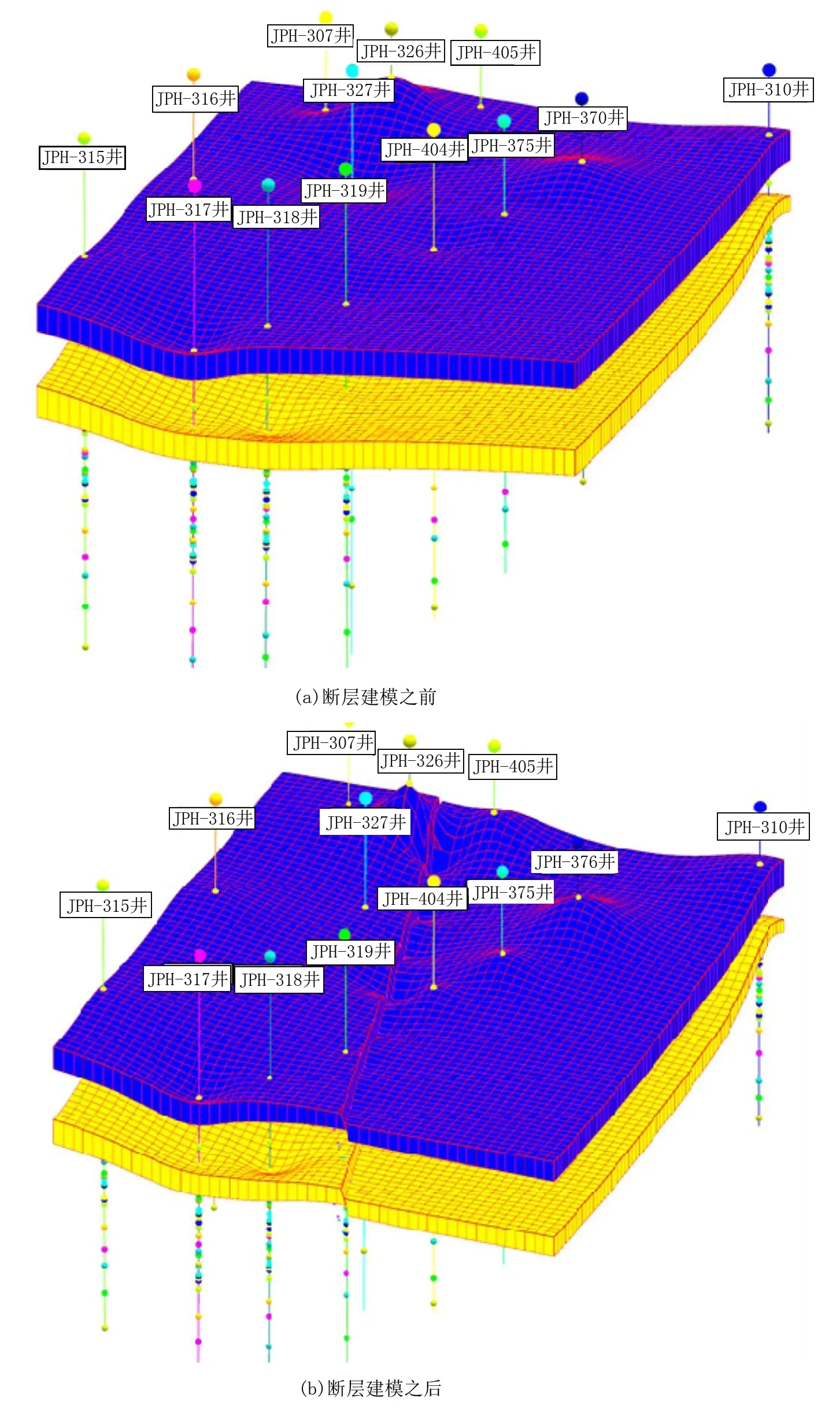
图4 三维地质断层模型Fig.4 3D geological fault model

1)保证数据结构稳定。传统的方法[8,13,15]是六面体直接被断层面切割，会导致一个六面体被切割为2个不同类型的体，不能保证一分为二后的体都为六面体(8个角点)，其结果不仅会导致六面体元结构不统一，造成体元表达困难，而且增加了体元个数，不便于模型的数据管理和运算处理。该算法在不修改每个六面体元具有8个角点的数据结构条件下，通过对角点坐标进行移位，能够全面分析并展示平面剖切六面体元的情况，同时不修改体元数据量，为后续模型的分析应用提供了方便。

2)降低时间复杂度，提高建模效率。该算法通过对已经生成的三维模型六面体网格进行处理，计算断层线与角点网格的交点及交点高程，对相应六面体元角点坐标进行移位，使之自适应断层面，从而能够快速地完成断层模型的生成。