以操作过程观照学生的概念理解水平

毛艳津

【编者按】数学学科素养是具有数学基本特征的、适应学生个人终身发展和社会发展需要的思维品质与关键能力。在当前书面测评仍是评估学生学业水平的主要方式的情况下，为适应学生未来发展的需要，教师如何以学生学科素养发展为导向，对传统测评方式做出创新设计，如何优化考查内容并有效利用反馈数据，成为亟待解决的问题，本期话题一起来探讨。

概念本质特征的建构水平，一般表现在学生对相关概念的理解与应用中。对概念理解水平的考查，有时候不能用一些简单的客观题加以实现，而是需要通过一些有过程性材料呈现的测评才能作较为深入的分析与了解。比如说对“圆概念”的理解，只是设计一些诸如“一个圆的直径是3厘米，那么这个圆的半径是（  ）厘米”这样的习题，还不能全面考查学生对圆概念的理解水平，而且通过此类习题最终获得的测评数据也只能反映学生对相关概念单一层面的了解，而无法从能力与素养维度了解学生的整体理解水平和学习状况，因此这样的监测结果对实际的教学指导与改进缺少足够的支持。唯有设计有过程视角的，反映学生能力与素养水平的测评题，才能从更加全面的角度了解学生的学习状态，找到学生学习过程中的问题所在，从而提出更有针对性的教学建议。

本文以某校小学六年级（第一学期）数学“能力素养”监测卷中的一道关于“圆的认识”的操作题为例，谈一谈基于学科素养立意测评题的设计、数据分析，以及改进“圆的认识”一课教学的建议，以供一线教师参考。

原题：王老师想从一张边长为20厘米的正方形纸片中剪一个最大的圆。请在右图中画出这个最大的圆，并将画的过程记录下来。

我们先来看此题的测评意图。从知识层面分析，本題检测学生对“圆的特征”的理解水平，体现为两个层次：层次一，概念的认识，即对“圆心确定圆的位置，半径确定圆的大小”的认识;层次二，简单应用，即能够应用概念特征解决问题。再来看素养层面，本题测评中还有“将画的过程记录下来”的要求。显然，我们不仅想看到结果，还想通过看到学生完成任务的过程印记，了解学生在画圆过程中表现出来的不同能力水平与素养差异。

从测评结果来看，本题的正确率为58%，有超过一半的学生，能够在此正方形中正确画出圆，且过程印记也比较清晰、合理。而有42%的学生，作答过程存在着不同程度的缺陷。再对作答错误的情况进行分析，可以发现学生错误作答（包括不够严谨的）的情况主要表现为三类：一类是完全错误（包括没做），占错误人数的11%;一类是凭感觉在正方形内作图且接近正确答案的，占错误人数的13%;还有一类位置、大小两个维度只考虑其中一种情况的，占错误人数的76%。

具体可以用以下表格加以呈现。

结合上表，我们再将知识、能力、素养等综合起来对错误（或不完善）的答案反映出来的学生的学习水平进行深入剖析。

如果将“概念认识与应用割裂”作为概念理解的一级水平，那么这个水平层次的学生，虽然记住了概念，如“圆有圆心、半径”等要素，知道“半径能够确定圆的大小”等概念，却不能结合情境加以简单应用。笔者认为，这样的学习仍然属于机械性的，尚未实现知识与能力的转换，更没达到信息加工与回馈应用的素养水平。

我们可以将“对图形间关系的把握能力不足”作为概念理解的二级水平进行解读，处于此水平层次的学生，对圆的相关要素特征是理解的，比如“同一圆内，直径与半径间的2倍关系”等，但缺少与其他图形的联系与沟通，造成其在解决简单的整合问题时，概念知识的综合应用力不足，综合分析与知识提取的学科素养水平不高。

“整体把握图形特征的能力不足”反映的是学生动手操作解决问题的能力水平，与上一种“对图形间关系的把握能力不足”问题的不同之处在于，学生就圆概念的理解已经比较到位了，但在操作应用时思考问题不够完善，造成某一方面存在问题。从概念知识的应用与问题解决的状态来看，可以认为学生对圆概念的理解基本达成，但在借助操作工具呈现结果时，整体把控能力还有待提升。

通过对以上监测数据的分析，笔者思考：在教学“圆的认识”时，针对学生对圆概念的深度理解不足，综合分析与解决问题的素养不强的问题，是否可以将问题解决作为载体，引导学生从整体上认识圆的特征，理解圆中各要素间的关系，从而达到在帮助学生深度理解圆概念的同时，发展学生综合素养的目的。

一、从解释生活现象入手，引导学生对“圆的特征”的探索

圆在生活中有着广泛的应用，它到底有什么特征和奥秘？为什么生活中那么多物体的外形都要做成圆的？从生活中常见的圆引入，唤起学生对圆的认识的生活经验，并以“车轮为什么要做成圆的”这个值得探究的问题引发学生思考，进入到学习的状态。教学时，可分成两个层次。

（一）层次一：借问题引发学生对圆的特征的思考

师：我们在生活中见到的车轮都是圆的，可是车轮为什么要做成圆的呢？

1. 想象：我们用圆、正方形、椭圆代替车轮来滚一滚，想象一下会是怎样的呢？（用正方形、椭圆做车轮，物体在运动时会不平稳，没有办法滚动）

师：这都是同学们的推测，到底真实的原因是什么？圆有什么特征呢？

2. 观察：课件演示滚动的过程。

师：请你仔细看，它是怎么动的，和你想的一样吗？

比一比：你发现了什么？（圆的滚动轨迹是一条直线）

3. 思考：为什么滚动时圆的中心是在一条直线上呢？

结合视频，初步感知“圆，一中同长”的本质特征，即所有在圆上的点到圆心的距离是一样长的。

选择“车轮为什么做成圆的”这一问题进行实践探究：一是唤起学生对身边常见事物的思考，激活探究事物的好奇心;二是能够将具体活动与生活实例结合起来，更贴近学生的认知特点;三是借助问题思考与解释的过程认识圆的特征，增加了综合分析与思考的要求，利于发展学生的综合学习素养。

（二）层次二：从具体的事物，迁移到数学几何图形

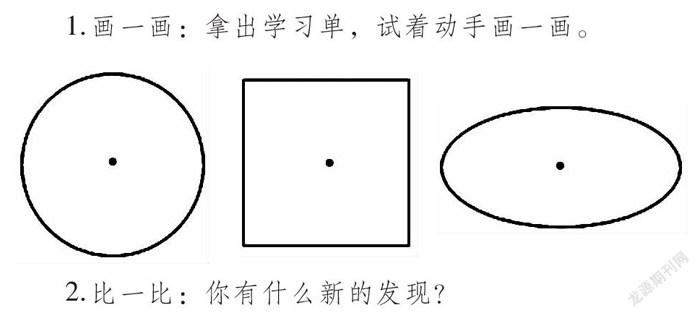
师：同学们，在模拟车轮滚动的实验中，我们发现中心点运动的痕迹就是中心点到地面距离的变化轨迹。拿出学习单，自己动手画一画，观察不同图形的中心点到它边上的距离，有什么不同？

1. 画一画：拿出学习单，试着动手画一画。

2. 比一比：你有什么新的发现？

发现：圆的中心点到图的边上的距离都相等。

3. 理一理：通过刚才的实验，我们发现车轮做成圆的是运用了圆的什么特征呢？

在这个过程中，学生通过探究椭圆、正方形、圆三种不同图形的中心点到边上的距离，在教师设计的画一画、比一比、理一理等系列活动中积累探究图形特征的活动经验，一步步引导学生在操作、观察与思考中发现，车轮做成圆的真正原因在于应用了圆的本质特征，即圆心到圆上的距离都相等。显然，在整体学习探索的过程中，因为有结合具体学习材料的操作、比较与讨论，对学生的数学活动经验的积累与综合学力的培养均相当有利。

二、结合有层次的练习，强化对“圆，一中同长”本质特征的理解

作为圆本质特征“一中同长”的两个核心要素：圆心和半径，其一决定了圆的位置，其二决定了圆的大小。只要有了圆心和半径，就决定了这个圆，也就决定了圆的周长与面积。因此圆心和半径对圆来说是最关键的，我们要让学生对此有深刻的认识，让他们在对圆的实际应用中能首先想到寻找圆心和半径。

例如，设计一组练习，强化学生对圆心和半径的理解。

1. 画规定大小的圆，r=1 cm。

2. 按要求画圆。

（1）以点O为圆心，画两个大小不同的圆。

（2）分别以O1、O2为圆心，画出半径都是1 cm的圆。

（3）请你在正方形里用圆规画一个最大的圆。

我发现：圆心决定圆的（  ），半径决定圆的（  ）。

此组练习，有圆的知识技能训练，也有结合其他图形的问题解决，从单一知识的巩固到综合性的简单应用，很好地帮助学生回归到以图形整体视角来认识圆，理解圆的一些特征。同时，“练”不是目的，“练中悟”“练中构”才是此组练习的目的，即希望通过此组练习，学生不但能巩固对圆特征的认识，还能够在比较、分析与发现、归纳等数学学习的基本方法层面有所得、有所悟。

三、拓展练习应用空间，丰富“圆的特征”的认识经验

当学生对圆的特征“一中同长”有一定的理解后，教师可以设计一些实践活动作为拓展练习，从而积累数学基本活动经验，发展学生应用知识解决实际问题的能力。

1. 用学过的知识解釋生活现象。

呈现课堂交流时出现的圆桌、井盖等图片，请学生再来解释“为什么要把它们做成圆的”。

2. 在操场上画圆。

提出问题：活动课上，同学们要在操场上做游戏，需要画一个半径是2米的圆，你有什么办法吗？

学生分组自主活动，借助皮尺、标志杆、绳子等物品画圆。

在数理层面上，学生理解了“一中同长”，并能够利用圆心和半径画圆。当然，我们不能简单地将学生引向“画圆只要用圆规就好了”的结果思维和操作技能上来，而是更希望通过本节内容的学习，能够深刻理解“圆内各要素间的关系”，并能以所学知识解释或解决一些实际问题，类似于前文要求学生“能用圆的特征解释生活中的实际现象”或“能不用圆规画一个圆”等。唯有通过此类问题的解答过程，才能最大限度地引导学生积累起“圆的认知”经验，逐渐发展“图形认识”的能力素养。

最后想强调的是，数学学科素养立意的测评，需要结合学生在学习相关知识内容过程中能力水平的解构与素养特征的描述，教师才能设计出有针对性的测评工具，从而获取相应的测评数据。比如，学生对“圆概念”的理解水平，教师至少要能够结合课程目标、学习目标梳理出两至三个水平层次，如前文中的测评意图分析。唯如此，能力立意、素养立意测评才会体现其不仅能诊断学生基础的学习水平，还能了解学生能力水平与素养水平，从而实现发展学生综合素养的意义。

（作者单位：浙江省嘉兴市辅成教育集团）

1484500511298