地震荷载作用下运营隧道的受力性状分析研究

作者简介：

周杰之（1986— ），高级工程师，主要从事公路工程投资、建设、运营管理工作。

摘要：文章为了获得在地震与车辆耦合作用下的隧道结构变形与应力分布情况，建立了三维有限元数值模型进行动力学分析计算。通过计算与分析表明：隧道地铁结构的最大变形值（28.05 mm）发生于地震峰值加速度时刻，其位于隧道的仰拱底部;在地震峰值加速度时刻，隧道结构产生最大的水平向剪应力，这在隧道工程设计中应引起重视。

关键词：地震;隧道结构;变形;数值模型;地震峰值加速度

中国分类号：U452.2+8A401463

0 引言

随着国家“一带一路”建设的推进，我国交通基础设施得到快速发展。截至2020年年底，我国投入运营的铁路隧道达到16 798座，总长约19 630 km，作为交通行业基础设施之一发挥着重要的作用。很多学者研究地震荷载下隧道的力学性状，例如，李笑穹等人[1]研究了地铁车站[CD*2]隧道连接段结构在地震荷载下的响应，其研究表明强震作用下的车站中柱顶、底端均会产生拉与压的应力，另外侧墙与土体会发生脱开的现象;刘妮娜[2]基于Marc有限元软件建立了含地裂缝的地铁隧道数值模型，探讨了地震激励下隧道结构的剪应力分布，并得出地震作用下隧道的底部产生最大的主应力与动加速度的结论。基于此，本文以我国西南地区某地铁隧道作为研究对象，探讨其在强震与车辆耦合作用下的受力与变形状况，以期为类似的工程设计与施工提供借鉴与参考。

1 数值工况简述与模型的建立

我国某西南地区为高烈度地震区域，该地区某市建设有地铁隧道，其中某段地铁隧道距地面埋深约45 m，隧道管片为钢筋混凝土，隧道半径为3 m（含隧道厚度0.3 m）。本文结合圣维南原理建立三维有限元数值模型，模型的尺寸取隧道半径的3～5倍，其长、宽、高分别为90 m、20 m、60 m，其计算模型如图1所示。模型均选用C3D8R进行网格划分，共划分为36 482个单元。

建立的模型尺寸是截取地铁的有限段分析，因此模型的边界条件必须要参照实际工程进行设置。在算例当中，模型的顶部处于自由状态，而底面与左右面均为约束的状态。因此，固定模型的底部位移，即限制X、Y与Z方向的移动（U1=U2=U3=0），模型的左右两侧限制X与Y方向移动（U1=0），其余面均为自由态。根据岩土地震工程学，假设地震发生于无穷远处，其释放出的部分能量通过土体介质以[JP+2]剪切波（横波）和压缩波（纵波）的形式传播至地面，当剪切波到达地面时，其振动最为强烈且对地面的构筑物影响损坏最大。同时，许多研究也表明，构筑物因地震而引起的破坏主要是来自于剪切波。因此隧道地铁在进行地震荷载的分析时，主要考虑水平地震荷载的作用，并对模型作位移的约束，即底部约束X与Y两方向的位移（U1=U2=0），左右两侧仅约束Y方向的位移（U2=0）。

1.1 模型参数的选择

在保证精确度的前提下，为了减少计算量，本文对模型进行了简化。为此，对模型的建立和分析计算提出了以下5个假设：（1）在地震作用前，土体与隧道在自重应力状态下固结，土体原位应力和性状的改变不考虑;（2）不考虑地震的过程对土体力学参数的影响，不考虑渗流的影响;（3）隧道为理想弹性体，周围土体为弹塑体，服从Mohr-Coulomb库伦强度准则;（4）该地铁隧道里的地铁车辆作用等效为静荷载的形式（采用的荷载标准值为10.5 kN/m）。

另外，通常在路基或岩土工程分析中采用土体的内摩擦角（φ）和粘聚力（c）参数计算土体在受外部荷载作用下其内部各应力应变的状态，在满足工程上的精确度后又能提高工作的效率，因此通过对本隧道地铁获取现场土样，对其常规的力学相关参数进行试验以获取数值仿真计算所需的参数。

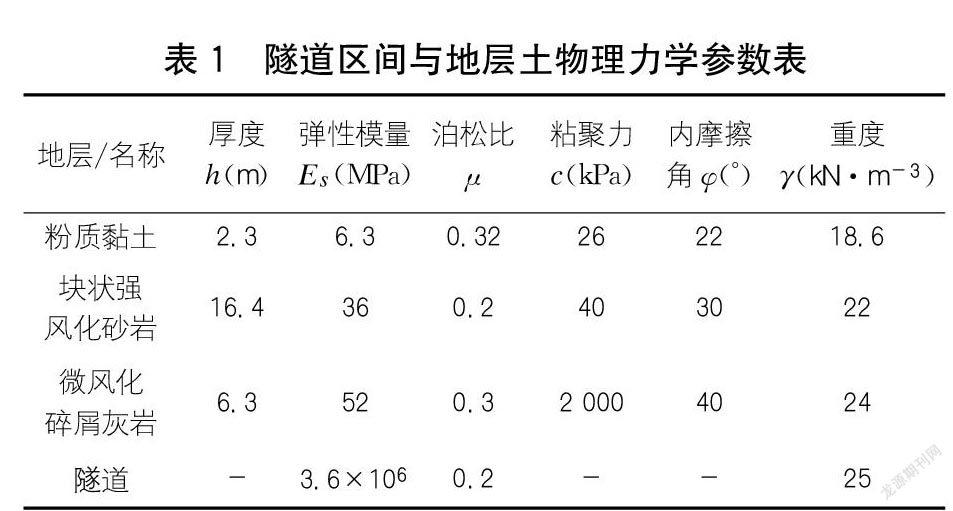
其中，测取土样的密度时利用环刀法测量土样的密度，将备好的环刀（内径为6.8 cm）在其內壁涂上凡士林，对重塑的土样进行切成型、整平，而后再烘干测量。结合现场快速、不排水填筑施工的情况，本次试验采用应变控制式直剪仪对每组试验制作三个土样进行快剪试验，以获取更贴近现场的实际参数，即抗剪强度的黏聚力与内摩擦角参数。土层与隧道的计算参数如表1所示。

1.2 接触面的设置

考虑到隧道地铁结构与地基土层之间的材料力学差异较大，其隧道结构与土层间存在着界面摩擦作用，因此需对其设置界面摩擦接触面，以模拟地震荷载下可能发生的相对滑移现象。在本文当中，对隧道-地基土层之间的接触采用Coulomb摩擦模型进行表征，其接触面间的接触压应力为p，则摩擦模型中的极限摩擦力值为τcrit=μp，其中μ为隧道结构与地基土层间的界面摩擦值，通常取值μ=tanφ。本次计算μ=0.4[3-4]。

1.3 地震波的选取与阻尼的设置

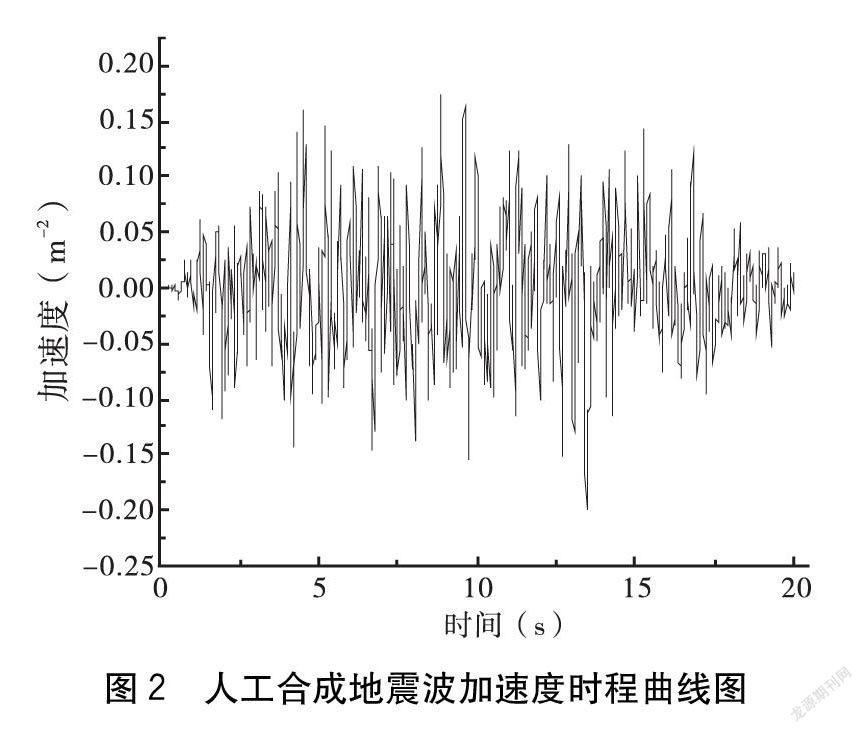
在岩土工程中，对地震波的选取计算通常基于以下几种方法：（1）根据地震工程原理合成地震波;（2）按照已有的强震地震波记录进行计算;（3）将地震波等效为正弦或者余弦剪切波进行数值计算;（4）根据设计规范反应谱，进行合成人工地震波。本文采取第四种方法，即基于公路工程抗震设计规范反应谱进行人工合成地震波，按照《中国地震动参数区划图》[5]可确定该区域抗震设防烈度为8度，Ⅱ类场地，进而得出水平设计基本峰值加速度为0.2 g，为此合成的该地震波其水平向的动峰值加速度为0.2 g，其时间间隔为0.02 s。为了节省计算时间，本文选取该地震波的前20 s激励于模型底部，进行动力分析的计算。其地震波形图如图2所示。

通常，在动荷载的作用下物体会发生被迫运动，但随着时间的推移，物体消耗大部分的能量，直至停止运动，这一过程称之为物体的阻尼作用。在ABAQUS软件中，对动力的分析总共提供了4种设置阻尼的方法，分别为直接模态阻尼、结构阻尼、整体阻尼及瑞利阻尼。在本文的数值计算中，采用瑞利阻尼的方法设置，即阻尼为物体质量与刚度的线性组合。

对土层与隧道体结构设置阻尼作用，在实际工程中采用瑞利阻尼可满足工程上的精确度，通常取结构体的前两阶自振率计算，即取i=1与j=2。本文对土层与隧道结构体进行第一阶与第二阶振型的阻尼比取为0.05[6]。

2 数值计算结果分析

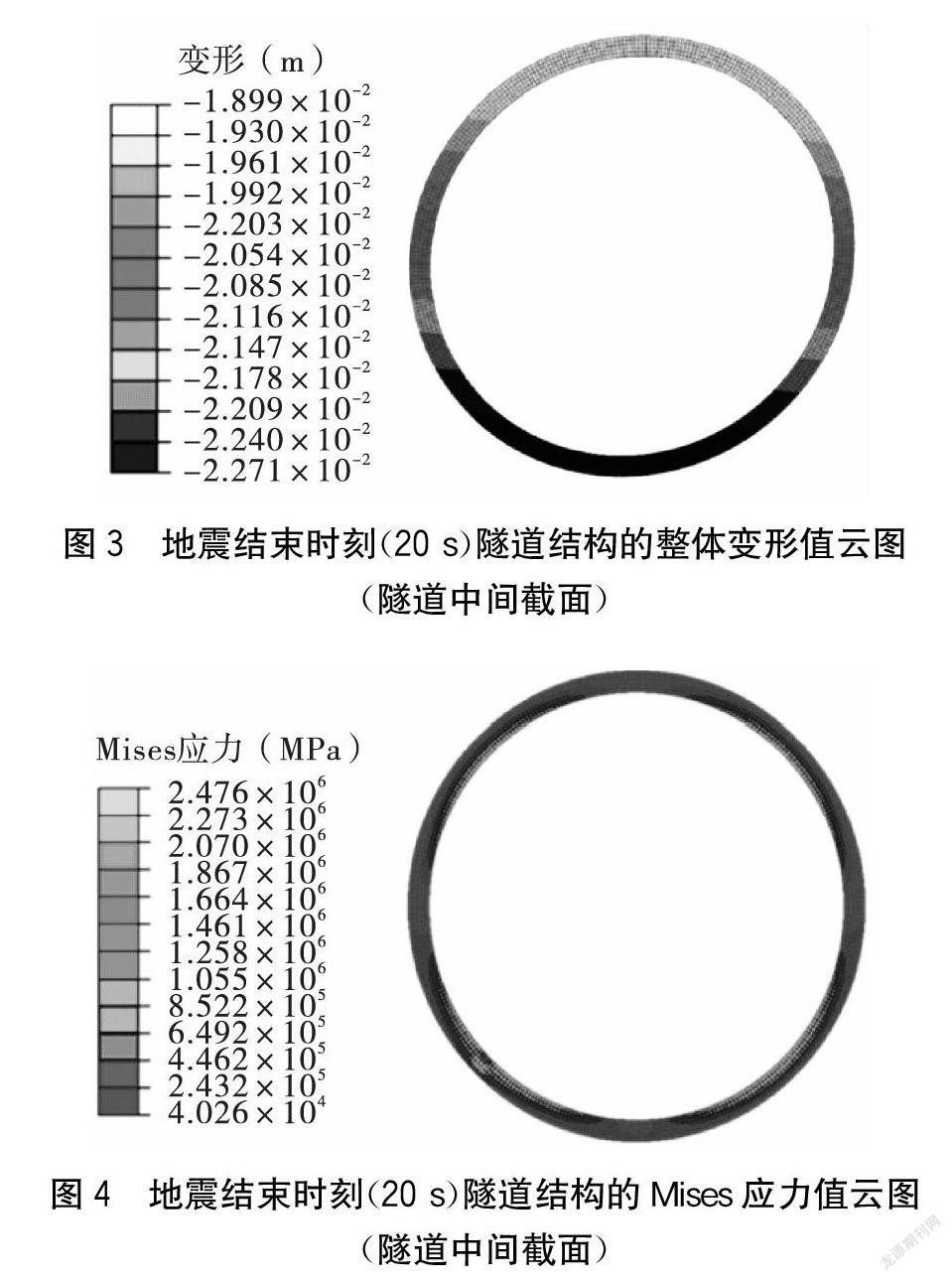
在强震的作用下，隧道结构受到附加荷载的作用，产生较大的变形与内力作用。提取隧道中间断面在地震结束时刻的总变形与米塞斯应力的分布值，分别如图3与图4所示。图3显示，在地震结束后，隧道中间断面的最大位移发生于其底部，该值为22.71 mm。由图4可知，隧道中间断面的最大米塞斯应力为2 476 000 MPa。

2.1 地震作用下隧道结构时程变形与应力的分析

据已有研究表明，地震作用下的结构所产生最大

位移与应力值均发生于地震的过程中。为此，本文分别提取隧道拱顶与仰拱底部的时程位移与应力曲线。其中，隧道的仰拱在地震峰值加速度时刻（13.44 s）达到最大位移值28.05 mm;隧道的拱顶在10.04 s时达到最大位移值21.73 mm。隧道拱顶与仰拱底部均在靠近峰值加速度时刻达到最大水平应力值，其底部水平应力为-3 531 000 MPa，拱顶的水平应力值为1 712 000MPa。由此说明，在地震作用的隧道承受到水平剪应力较大。

3 结语

本文基于ABAQUS有限元数值计算研究了隧道地铁结构在地震作用下的变形与受力状况。其中，数值计算大致可分为两步骤，先是使隧道结构与周围土层获得地应力而无位移的状态，在地应力平衡后再对其进行施加地震动荷载的计算。通过计算分析，在水平地震作用下，隧道地铁结构会与周围土层发生局部的脱开现象。另外，隧道结构在地震峰值加速度时刻达到最大位移。

参考文献：

[1]李笑穹，李忠献.地铁车站-隧道连接段结构地震响应分析[J].北京工业大学学报，2014（8）：1 213-1 218.

[2]劉妮娜.地裂缝环境下的地铁隧道-地层地震动力相互作用研究[D].西安：长安大学，2010.

[3]路德春，王 欣，罗 磊，等.土与结构接触特性对地下结构地震反应的影响研究[J].防灾减灾工程学报，2017，37（2）：177-186.

[4]罗 磊.土与结构接触特性对地下结构地震反应的影响研究[D].北京：北京工业大学，2016.

[5]GB 18306-2015，中国地震动参数区划图[S].

[6]姜 龙.城市地下综合管廊典型节点地震响应分析[D].南宁：广西大学，2018.

[7]晏启祥，张 煜，王春艳，等.剪切波作用下盾构隧道地震效应的拟静力分析方法研究[J].工程力学，2015（5）：192-199.

[8]孙靖云，陈利琼，夏 燕，等.地震载荷工况下隧道内油气管道应力分析研究[J].应用力学学报，2017，34（4）：795-801.

3993501908229