让生成性课堂活力飞扬

张洁

[摘  要] 随着新课改的提出，不少教师更新了自身的教学理念与教学方式. 文章在“以学为本”的教学改革的推进下，通过对教学案例的分析，探讨了构建生成性课堂的策略：合理设计具有弹性的情境，为生成营造氛围;加强师生间的互动交流，给生成一个支点;以巧妙设问完善课堂探究，铺就通向生成的路径.

[关键词] 新课改;课堂教学;生成性课堂;探索

传统教学模式下，教师习惯于将教学视野局限于理论层面上，或浅析概念，或解题应用，致力于探究数学知识和引导运用方式，导致的结果是，表面上学生可以按照一定的模式去解题，实则学生的创造性思维和灵活性思维逐步减弱，并没有真正理解数学概念、定理的本质.

新课改风向标下，数学课堂教学改革强调学生在教学中的主体地位，关注学生的发展，使得与之匹配的各种各样的教学方式应运而生，这在很大程度上改进了数学课堂教学的现状，提升了学生的学习能力. 笔者在推进这种“以学为本”的教学改革中开展了生成性课堂教学的实践研究，对课堂教学模式进行反复试验与矫正，取得了一定的进展，现将具体的实施策略抛出，与同行们一起探讨交流.

[⇩] 合理设计具有弹性的情境，为生成营造氛围

由于生成性课堂教学是建立在充分预设之上的动态生成，从而，教师需对学生的需求有一个准确的判断，合理设计有效的、具有弹性的教学情境，来为学生的有效生成营造氛围，并在课堂教学进程中不断调整教学策略，以促进学生更加富有个性、更加有效地学习数学.

案例1 以“点到直线的距离”的教学片段为例

问题情境：如图1，已知平面内的一点P（x，y）与直线l：Ax+By+C=0，试求出点P到直线l的距离d.

经过一番探讨之后，学生如笔者预设一般得出课本中呈现的常规解法和等积法这两种解法.

师：好，对于这一题的探究就进行到这里，下面……（此时，忽然一名学生举手. ）

生1：老师，我还有其他的求距离d的方法. （这名学生的回答显然已经与笔者课前的预设有较大的出入. 笔者本想岔开话题进入下一环节的学习，但又觉得不妥.）

师：看来，有同学的确如老师所愿进行了有效的课前预习. 生1，你说一说呢？

生1：其实这里只须设求出点H（x，y）的坐标即可.（此时，有的学生面露狐疑，有的开始演算. 笔者对这一方法没有进行充分预设，脑海中无法显示完整计算过程，此时，何不与学生一起试着探究一番.）

师：你的方法非常独特，不过这种方法老师也没有研究过，能具体说一说吗？

生1：设H（x，y），则有Ax+By+C=0，而k=，所以=，则B（x-x）-A（y-y）=0. 由Ax+By+C=0，可得Ax-Ax+By-By=-C-Ax-By，所以A（x-x）+B（y-y）=-（Ax+By+C）.

师：很好！老师明白你的想法了，那接下来该如何得到距离d呢？下面给大家一些时间，通过合作探究尝试找出答案.

……

课堂上的思维火花源于学生的创造性思维，它们都是稍纵即逝的，需要教师用心采摘. 以上案例中，原本的预设是推导与运用公式，但教师尊重课堂教学的可生成性资源，通过合理设置教学情境将课堂教学的重心放在了推导公式上，弱化了公式的运用，将其作为课堂的点缀. 这样的教学过程，看似没有实现教学目标，实则由于教师给予了学生共同思考、探究和发现的空间与机会，有效地培养了学生的探究性思维，促进了课堂教学的动态生成.

[⇩] 加强师生间的互动交流，给生成一个支点

数学课堂教学中，教师、学生、教材间的多向交流和多边互动是形成生成性课堂的关键所在，而在这样多角度的活动下，师与生的互动尤为重要. 现代教学论认为，一节课成功与否主要在于学生在参与中是否实现自主成长与进步，那么，倘若教学中缺了學生的参与，少了师生间的互动，无论教学语言多么精彩，教学内容多么丰富，教学手段多么高明，都无法发挥真正的教学价值. 所以，生成性课堂教学需要加强师生间的互动与交流，创造和谐平等的师生关系，充分调动教与学的积极性，给课堂教学一个生成的“支点”，建构生成性数学课堂.

案例2 以一道数学竞赛题的探究为例

问题：设单位圆O内分布着60个点，求证：在☉O上有一点P，使得该点到这60个点的距离之和不超过80.

师：因为这是一道国际数学竞赛题，所以难度肯定是有的，大家有没有信心解决它.

（学生信心十足，志在必得）

师（拾级而上）：我们在日常生活中，是不是觉得同伴互助可以带来更多的便利？其实，在解题中亦是如此. 本题可以用什么方法呢？

生1：可以试一下构造的思想.

师：如何构造？

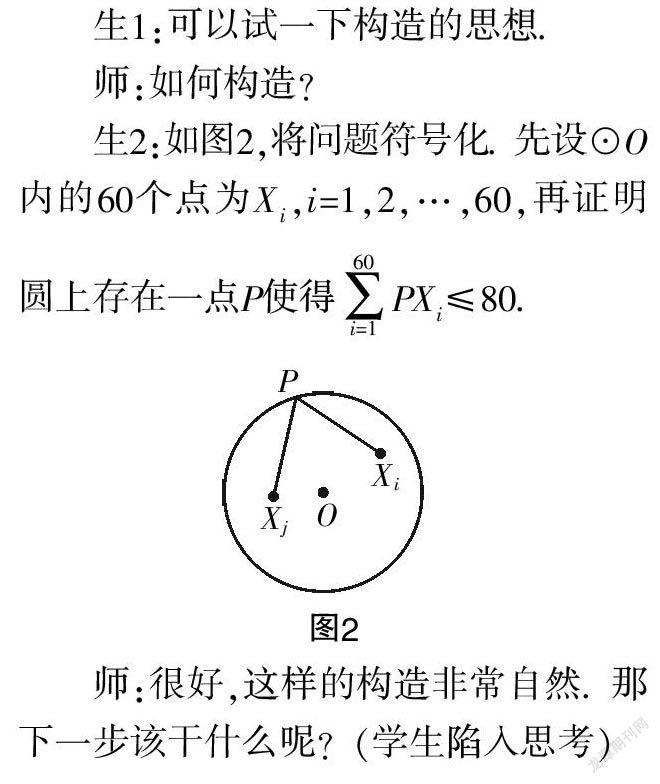
生2：如图2，将问题符号化. 先设☉O内的60个点为X，i=1，2，…，60，再证明圆上存在一点P使得PX≤80.

师：很好，这样的构造非常自然. 那下一步该干什么呢？（学生陷入思考）

师（点拨）：是不是该找寻点P的“同伴”呢？大家看，对于☉O上的任一点P，都有PX<弦长≤直径=2，即PX<120，而此处需要证明的是圆上存在一点P使得PX≤80. 该如何是好呢？（学生思考片刻后，豁然开朗）

生3：可以找寻到点P所在直径的另一个端点Q，借助圆与直角三角形的性质求解.

师：很好，谁能简要说一说解法.

师：哇！通过构造出点Q，我们距离成功越来越近了. 下一步该做什么呢？

生（齐）：再找一个“伴”.

……

从生成性的角度，我们可以发现教师注重与学生的沟通和交流，有目的、有意识地采用教学策略促使学生有效地进行生成性学习，促进学生思维的深化，让学生在深入思考下进行构造，优化学生的创造性思维. 在策略运用的过程中，教师不仅关注到以生为本的理念实施，还充分认识到问题的核心价值，使得学生成为学习探究的行动者，促进了课堂中的动态生成，同时提升了教师的课堂教学艺术.

[?] 以巧妙设问完善课堂探究，铺就通向生成的路径

在充满生成的课堂中，不仅要关注情境的创设和师生的交流，更重要的是通过设计精巧的问题来完成课堂探究. 设计精巧的问题，让学生积极主动地参与到问题的探究中去，鼓励学生亲身经历数学知识的产生、发展和应用，铺就通往生成的路径.

案例3 以“函数的恒成立与存在性问题研究”的教学为例

问题1：已知函数f（x）=-ax+4，对于任意的x∈[1，2]恒有f（x）>0，试求出实数a的取值范围.

问题2：已知函数f（x）=x2-ax+4.

（1）任意x∈[1，2]，恒有f（x）>0，试求出实数a的取值范围;

（2）存在x∈[1，2]，有f（x）>0，试求出实数a的取值范围.

问题3：已知函数f（x）=x3-ax2+4，对于任意的x∈[1，2]恒有f（x）>0，且a>0，试求出实数a的取值范围.

问题4：根据题意编写题目，并解答. （在____上填“任意”或“存在”）

已知函数f（x）=x3-ax2+4，g（x）=ax2+4（a>0）.

（1）_______x∈[1，2]，_______x∈[1，2]，有f（x）>g（x）成立;

（2）在（1）的情况下，试求出实数a的取值范围.

数学育人的本分在于培养学生的思维习惯，发展学生的理性精神. 单从这一点来看，数学就是不断探索和自然生成的过程. 以上案例中，教师以学生的已有知识结构为起点，朴素地提出数学问题，课堂中没有花哨的教学手段和空泛的教学活动，只有学生的合作探究和教师的实时点拨. 从一次函数到二次函数，再到三次函数的研究都是由简单的数学模型串联而成的，并依照恒成立和存在性这两种模型去解决问题. 在逐层探究下，学生自然逼近数学本质，强化了对数学本质的思考，加深了对数学本质的理解，使得数学思维有了价值性的提升，学生的创造性思维得到长足发展. 在这一过程中，教师铺就通向生成的路径，同时彰显智慧教学的魅力.

总之，生成性是新课程课堂的基本价值追求，着重关注学生的成长. 动态生成的教学方式要从特例走向常态，需要教师合理设计具有弹性的问题情境，加强师生间的互动交流，以巧妙设问完善课堂探究，真正使数学课堂教学焕发生命的活力. 愿教师的“教”充满灵性，学生的“学”充满悟性.

3808501908296