基于问题引领的课堂设计

刘洋　刘春红

[摘  要] 以对数的运算性质为例，立足问题，引领、引导学生探究，揭示知识的本质，培养学生思维的深刻性，以促进学生数学核心素养的生成.

[关键词] 对数;性质;问题;高中数学

问题的引出

数学，从某种意义上讲，也是一门逻辑学，处处讲究严密的推理. 限于篇幅，高中教材的一些定理或公式的推理过程往往被弱化了，呈现给学生的大多是结论，这就需要教师补充被教材忽略的内容. 以对数的运算性质为例，教材只是给出了有关公式，没有详细加以论述[1].为了让学生能知其然并知其所以然，笔者认为，有必要引导学生进行探究，揭示知识的本质，培養学生思维的深刻性. 基于此，笔者以问题为导向，设计了一堂对数运算性质的探究课.

课堂设计

1. 创设情境，明确目标

问题1：不借助于计算器，你能很快地计算出下列式子的值吗？

（1）64×128;

（2）8192÷256;

（3）642;

（4）.

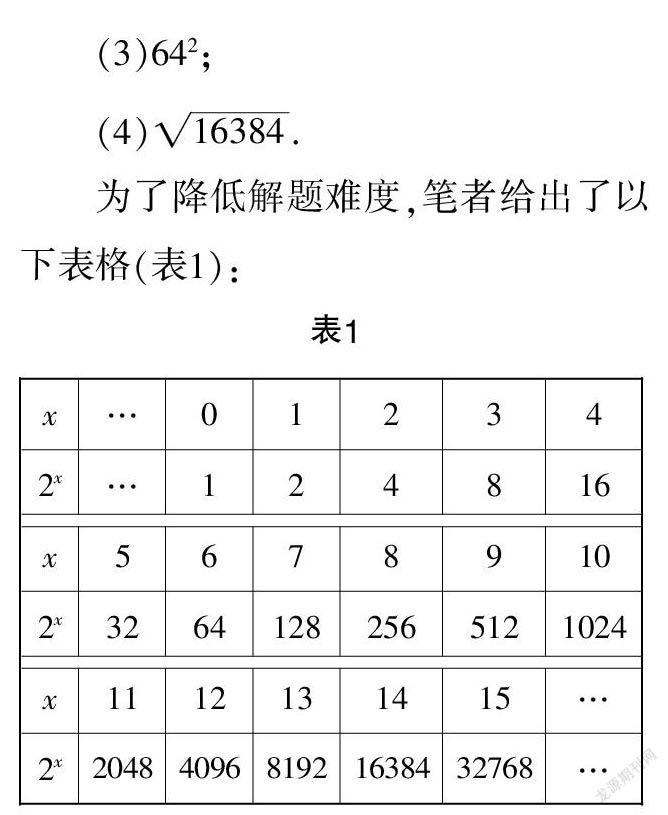
为了降低解题难度，笔者给出了以下表格（表1）：

学生惊喜地发现，借助于表格可以快速地求出各式的值.

问题2：为什么可以计算得如此快速？

学生马上说道：先将各式中的数都表示成同底数幂2a的形式，然后借助于指数运算性质可以快速地计算出来.

问题3：以第（1）题为例，64×128=26×27=213=8192，这是从幂的角度出发的.如果从指数的角度出发呢？

学生能很快答出：6+7=13.

问题4：6，7，13分别是哪个数的指数，如何求指数？它们之间有怎样的等量关系？

学生认为，6=log264，7=log2128，13=log（64×128），进而得出log264+log2128=log（64×128）.

问题5：通过上式的解答，你得到了什么启发？请计算1025×365.

学生计算1025×365时受挫了，因为出现了不同底数的幂的运算，没有运算性质可以运用. 此时启发和引导学生：64×128能够迅速计算出结果的根本原因在于两数可化为同底数幂的形式.基于此，着力点找到了：可先将1025×365的两数化为同底数幂的形式. 那么该化为以多少为底数的幂的形式呢？因为日常计算中，通常是用十进制表示一个数，可引导学生将两数化为以10为底数的幂的形式. 那么365该怎么表示成以10为底数的幂的形式呢？这时就将问题5转化为了学生熟悉的对数（此时也正好考查学生在上节课中是否真正掌握了对数），得到1025×365=1025×1065×lg3=1025+65×lg3.

2. 观察对比，认识关系，建构联系

问题6：通过上述例子，你对大数的计算有何想法？当M，N为两个很大的正数时，如何计算M·N的值？

通过上述例子的铺垫，学生基本能够想到将正数M，N表示为同底数幂的形式，但是不确定以何为底数. 为了引出本课的主题，笔者引导学生将其化为以a（a>0，且a≠1）为底数的幂的形式.

问题7：正数M，N为什么可表示成以a（a>0，且a≠1）为底数的幂的形式？该如何表示？

通过几何画板画出函数y=ax（a>1）的图像，再画出函数y=b（b>0）的动态图像，通过滑动参数b发现：无论b如何改变，两函数的图像都存在唯一交点.这时学生能够发现：当b=M时，该交点的横坐标就是此时的指数.通过简单的指数式化对数式，写出M=alogaM，N=alogaN，这就是对数恒等式.

问题8：请分别从幂的角度和指数的角度写出计算过程.

幂的角度：M·N=alogaM·alogaN=alogaM+logaN;

指数的角度：loga（M·N）=logaM+logaN.

这时学生发现这个过程不仅给出了对数的第一条运算性质“loga（M·N）=logaM+logaN”，而且给出了该运算性质的证明过程. 而这一切都是基于非常自然合理的探究过程的，有效避免了这个公式“从天而降”的尴尬与证明过程的“唐突”.

问题9：当M，N为两个很大的正数时，如何计算的值？不妨从上述例子借鉴一下技巧.

幂的角度：==alogaM-logaN;

指数的角度：log=logaM-logaN.

3. 创设新的情境，培养学生思维的灵活性

问题10：请参考对数表（以10为底数），试比较2100和365的大小.

基于问题7的提前预设，学生能够想到任何一个正数均可以表示成一个给定常数的幂的形式，于是将两数均表示成以10为底数的幂的形式，然后通过查对数表比较两数的大小.

问题11：对数表是如何制作的？现以10为底数，你能提供怎样的制作思路？

通过逐步逼近的方法的使用（借助于计算器让学生演示逼近的过程，逐步渗透“二分法”的思想），逐个得到使得10x=1，2，3，4…的x的值.

问题12：大家基本对对数表的制作过程有了大致了解，我们发现这是一个工作量很大的工程，尽管理论很简单，但是操作起来非常麻烦. 接下来请大家计算log365等于多少. 除了重新制作以3为底数的对数表外，你还有其他办法吗？

引导学生使用方程思想去计算，设log365=x，转化为指数幂的形式3x=65. 因为已知以10为底数的对数表，于是将指数式的两边同时取以10为底数的对数，得到xlg3=lg65⇒x=. 然后查阅对数表，就可以计算出log365的值了.

这里学生如果不理解为什么要将指数式的两边同时取以10为底数的对数，可以向学生解释这是从指数的角度表示的等式.

问题13：如果事先给一张以c（c>0，且c≠1）为底数的对数表，请计算logab（a>0，且a≠1，b>0）等于多少. 这一问题的提出，可以很好地解释为什么要研究换底公式，为什么可以换底.

问题14：（开放性问题）试判断2100是几位数.

研究一个指数幂形式的大数的数量级是天文学需要解决的一大难题，而换底公式恰好可以完美地解决这个问题.

结论：假设一个正的大数为N，则它是[lgN]+1位数.

一点感悟

世界上的任何角落，数学家都不是“无土栽培”而产生的. 而“土壤”源于课堂，“养分”始于启发，探究始于问题[2]. 传统的灌输式教学往往给学生制造了一种“好事者故意为之”的牵强与不自然，没有正常合理的问题导向、任务驱动，缺少必要的探讨和交流，长此以往，学生的思维仍在原地打转，数学思想自然无法形成.

数学思想是内在的，数学方法是数学思想得以体现和实现的有效手段之一. 而数学思维比数学方法更深刻，它更能反映数学对象间的最本质的内在联系[3]. 从对数的发展历史来看，最初动因就是为了解决天文学中出现的一系列大数的计算问题. 当然，在教学过程中，教师无须重现这一历史进程，但需要教师艺术地加以“浓缩”，通过师生合作研究学习，让一系列思想方法在课堂再现.

学习数学的目的是应用数学，教师在引导学生完成基本的数学建构后，可进行恰当的变式和拓展训练，进一步提出更为深刻的问题，这是促进学生思维发展的关键步骤. 当然，这也是数学发展（由简单到复杂）必经的过程.

参考文献：

[1]  黄光玉. 从历史过程中找寻数学知识的意义——“对数的运算性质”教学思考[J]. 数学通报，2020，59（10）：46-52.

[2]  杨军，布威麦尔耶姆·艾力. 基于理解的“对数运算性质”教学设计[J].中小学数学（高中版），2019（06）：35-37.

[3]  张灿. “对数的概念与运算性质”教学设计与反思[J]. 中国数学教育，2019（08）：28-30+33.

3859501908236