冻融循环和不均匀冻胀下寒区隧道的塑性解答1)

张常光 *, 高本贤 ** 周 渭 * 李海祥 *

* (长安大学建筑工程学院,西安 710061)

† (地质灾害防治与地质环境保护国家重点实验室,成都 610059)

** (长安大学公路学院,西安 710064)

引言

季冻区隧道含水围岩的负温冻胀受支护约束,产生的冻胀力反作用于支护上,对隧道安全造成不利影响[1-2].作为寒区隧道工程设计的重要环节,冻胀力解析计算已得到深入研究.Lai 等[3]利用黏弹性模型建立寒区隧道冻胀力的黏弹性解,Feng 等[4]假定围岩为各向同性均匀冻胀得到寒区隧道冻胀力的Mohr-Coulomb (MC)准则解答.实际上,寒区隧道围岩冻胀在3 个方向上是存在差异的,冷空气使得寒区隧道在径向上呈现明显的温度梯度,继而围岩冻胀表现为以径向冻胀为主,切向和纵向的冻胀次之且程度相同[5-6].Lü等[7]考虑围岩冻胀的不均匀性,基于MC 准则求得寒区隧道的冻胀力塑性解.

季冻区隧道围岩冻结圈形成后会经历长期冻融循环,每次冻融循环都将导致岩体一定程度的损伤、可能形成新裂隙,融化的水会充满裂隙再次冻结,如此循环使得围岩孔隙率升高、承载性能劣化,冻胀力也随之增大,最终造成支护开裂或因荷载明显增加而失效[8-9].前面所提到的寒区隧道冻胀力解答[3-4,7]均针对单次冻结,未考虑冻融循环对围岩承载性能的劣化效应.大量的岩石冻融试验表明[10-14]:冻融次数的增加会引发岩石的孔隙率增大,弹性模量、黏聚力和内摩擦角呈明显下降趋势,进而使岩石承载能力降低.刘泉声等[15]认为围岩冻融损伤伴随原有裂隙的发展、贯通以及新裂隙的出现.张慧梅等[16]利用CT 扫描研究了冻融岩石的细观损伤演化规律,指出岩石有效承载区随冻融次数的增加而减小.Liu 等[17]假设每次冻融造成岩石细观损伤的程度相同,基于弹性解答提出考虑冻融循环损伤的寒区隧道冻胀力计算模型;刘红岩等[18]引入未冻结围岩约束作用和冻融循环下微裂纹扩展规律及岩石冻胀率变化,改进了文献[17]中的寒区隧道冻胀力弹性解.

可见,目前鲜有冻融循环下寒区隧道冻胀力的解析计算,文献[17-18]已有研究只进行了弹性分析且未考虑围岩冻胀的不均匀性.当围岩承载能力低、冻胀显著或受高地应力作用时,季冻区隧道围岩易进入屈服状态,冻胀力的弹性解答不再适用.因此,本文合理考虑寒区隧道围岩不均匀冻胀和冻融循环劣化效应,以MC 准则为屈服判据推导寒区隧道冻胀力、应力与位移的塑性解答,同时给出相应的弹性解答,继而对所得结果进行可比性分析、给出适用性判定方法,并与文献塑性解答[7]进行对比验证,最后探讨冻融循环、不均匀冻胀和体积冻胀率对季冻区隧道性能的影响规律.

1 基本假定

为得到便于工程应用的季冻区隧道塑性解答,特做以下基本假定:

(1) 采用冻融圈整体冻胀模型[1],忽略围岩的实际冻胀过程,也不计隧道开挖和支护的时间,将铺设保温层、设置排水沟等防冻措施改善寒区隧道洞壁位移、冻胀力等现场数据变化的实际成效,通过综合对比本文理论计算结果纳入年冻融次数Na的调整.

(2) 圆形隧道受等值地应力作用(实际隧道断面非圆形按面积相等的当量半径转化为圆形[19]),支护与围岩的受力分析简化为平面应变绕轴对称问题,并以压应力为正.

(3) 隧道围岩属于以径向冻胀为主、切向和纵向冻胀次之且程度相同的不均匀冻胀,忽略冻胀对围岩物理力学性能的各向异性影响[5-7];冻结围岩为符合MC 准则的理想弹塑性材料,未冻结围岩不发生屈服;支护为均质弹性的等厚混凝土圆环衬砌,不考虑支护区混凝土的冻融损伤.

(4) 开放条件(在隧道施工和运行中均有地下水补给,使得冻结过程中的水分迁移显著,围岩也更易发生冻胀[20])下冻结围岩经N次冻融后的体积冻胀率为[11,21]

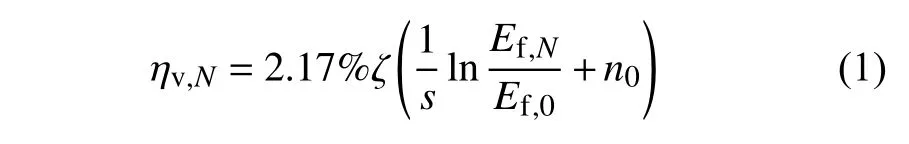
式中,下标N代表冻融次数与状态,0 代表冻结-未融化状态;ζ为水热迁移系数,取值与围岩冻胀敏感性有关[21],冻胀敏感围岩取1.58,冻胀非敏感围岩取1.0;s为拟合参数,可依据岩石冻融循环试验拟合获得;E为弹性模量,下标f 代表冻结围岩(后文亦有上标f,意同);n0为冻结-未融化状态下围岩的孔隙率.需注意的是,本文所有上/下标均指代唯一、全篇通用.

(5) 冻融循环造成冻结围岩的长微裂纹扩展但形状不变,文献[18]基于Griffith 断裂理论及细观损伤力学提出冻融循环下以长微裂纹条数变化描述冻结围岩弹性模量的劣化规律为

式中,ρo为单位面积微裂纹条数即微裂纹密度,lN为经N次冻融后的微裂纹扩展半长,lc为微裂纹分布参数;为第i次冻融循环所导致的微裂纹扩展半长;ω为微裂纹长轴与短轴的长度变化量之比;以上参数均可由冻融循环下岩石CT 技术获得;m为温度降低引起的围岩弹性模量放大系数,通常取1～ 2[18];KI为冰的体积模量.

2 寒区隧道弹塑性解答

寒区隧道冻胀力、应力与位移的弹塑性解答以冻结围岩是否进入屈服状态分为塑性解答(冻结围岩部分屈服)、弹性解答(冻结围岩未屈服).

2.1 塑性解答

由岩体冻胀性分级[19]和基本假定知,式(1)～式(2)对围岩均匀冻胀和不均匀冻胀均适用.假设冻结围岩已部分进入屈服状态,此时寒区隧道的塑性力学模型如图1 所示,其中季冻区围岩冻结范围可根据隧道多年实测温度场与当地经验或半解析法确定[22].在图1 中,ro为支护的内半径,r1为支护的外半径,rp为冻结围岩的塑性区半径,r2为冻结围岩的弹性区外半径;po为初始地应力,P1为冻结围岩与支护交界处的径向正应力,P2为冻结围岩与未冻结围岩交界处的径向正应力,Pp为冻结围岩弹-塑性交界处的径向正应力.

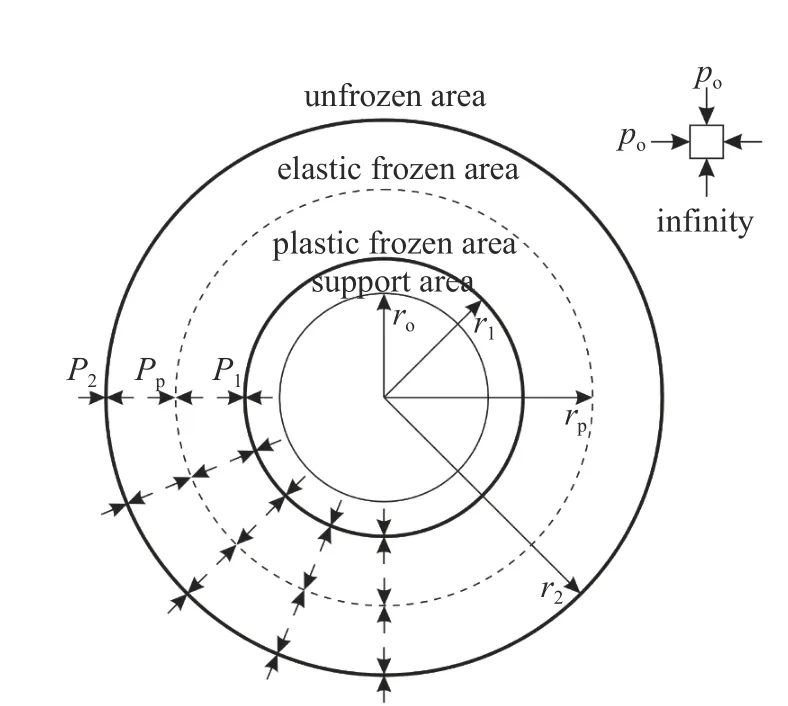
图1 寒区隧道塑性力学模型Fig.1 Plastic mechanical model of a cold region tunnel

在构建寒区隧道塑性解答时,未冻结围岩区和支护区均符合弹性力学的厚壁圆筒理论,冻结围岩弹性区以平面应变增量弹性本构方程为基础,冻结围岩塑性区需结合MC 准则,同时各区交界处要满足应力连续条件和位移连续条件(r=r1处支护区与冻结围岩塑性区交界、r=rp处冻结围岩弹-塑性交界、r=r2处冻结围岩弹性区与未冻结围岩区交界).

2.1.1 未冻结围岩区和支护区

根据弹性力学厚壁圆筒理论,得未冻结围岩区与支护区的应力分别为[23]

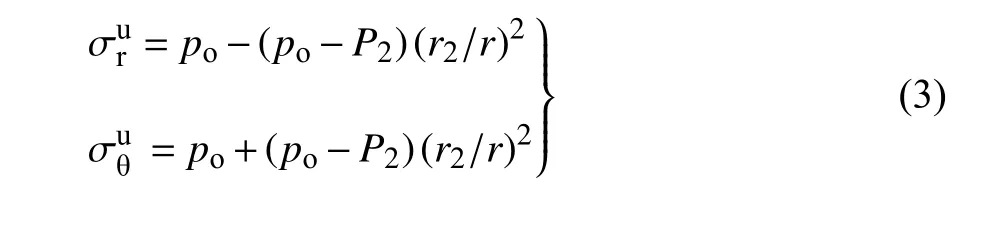
式中,σr为径向正应力,σθ为切向正应力;下标r 代表径向,θ 代表切向;上标s 代表支护、u 代表未冻结围岩(后文亦有下标s 和u,意同);r为极坐标下支护或围岩中某点到隧道中心的距离.相应的径向位移分别为

式中,u为位移,以指向隧道中心为正;μ为泊松比.

2.1.2 冻结围岩弹性区

冻结围岩线应变包括应力变化部分和冻结膨胀部分,其表达式即平面应变增量本构方程为[5]

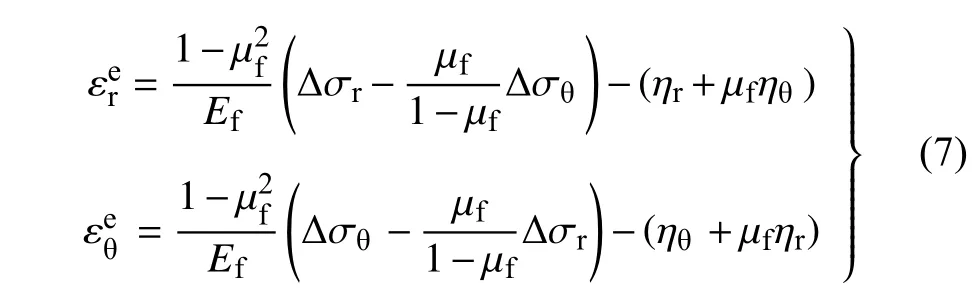
式中,εr为径向线应变,εθ为切向线应变,上标e 代表弹性状态;Δσr,Δσθ为径向与切向的正应力增量,且有Δσr=σr-po,Δσθ=σθ-po;ηr,ηθ,ηz为寒区隧道径向、切向和纵向的线冻胀率,且切向与纵向的冻胀程度相同即ηθ=ηz,体积冻胀率ηv=ηr+ηθ+ηz=ηr+2ηθ;不均匀冻胀系数k=ηr/ηθ,一般忽略冻胀过程中微/宏观裂隙扩展演化而假定为1～ 3 的常数[1],并有ηr=kηv/(k+2),ηθ=ηz=ηv/(k+2),冻结区水分的不均匀分布加剧了寒区隧道径向主冻胀,使得不均匀冻胀系数k和体积冻胀率ηv均有所增加.

冻结围岩的平衡方程为

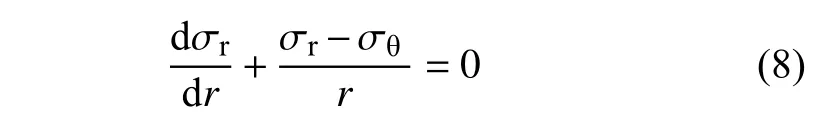
2.1.3 冻结围岩塑性区

以MC 准则作为冻融循环后围岩的屈服准则[24],在冻结围岩塑性区内σθ为大主应力σ1,σr为小主应力σ3,则

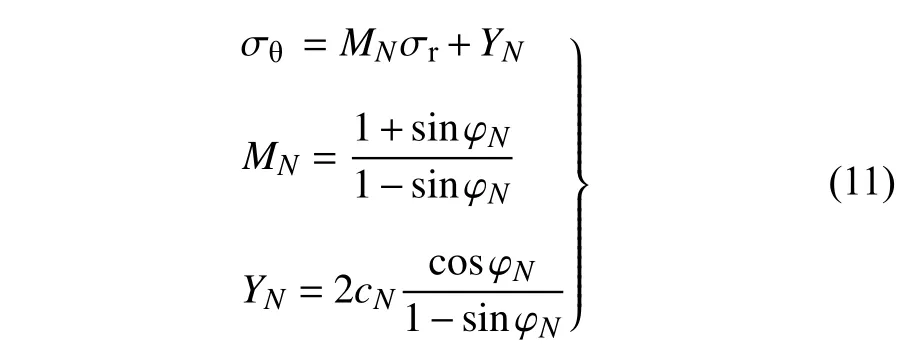
式中,MN,YN为方程参数;c,φ为冻结围岩的黏聚力和内摩擦角,且有[13]cN=ca+cbeαN,φN=φa+φbeξN,其中ca,cb,α和φa,φb,ξ均为拟合系数,可通过岩石冻融循环直剪试验确定.

联立式(8),式(11)和应力边界条件σr|r=r1=P1,积分得冻结围岩塑性区的应力为

式中,上标p 代表塑性状态.

采用线性非相关流动法则,结合几何方程εr=dur/dr,εθ=ur/r与式(7)和式(12),以弹-塑性交界处为位移边界条件,得冻结围岩塑性区的径向位移为

式中,β为剪胀特征参数.

2.1.4 冻胀力

在弹-塑性交界处冻结围岩弹性区的应力也满足MC 准则即式(11),则

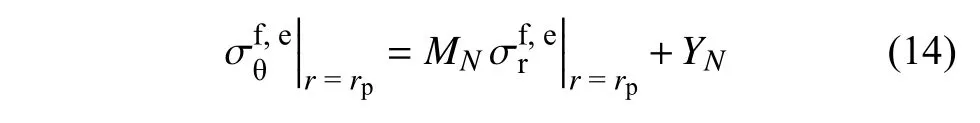
将式(15)代入式(6)并令r=r1,得寒区隧道的洞壁位移ua为

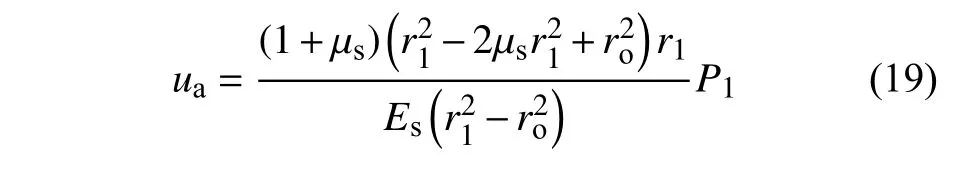
由式(15)求得的P1为总支护压力,包括冻结前围岩作用在支护上的初始径向正应力(按支护与未冻结围岩双层厚壁圆筒计算)[25],故寒区隧道围岩作用在支护上的冻胀力ΔP1为

2.2 弹性解答及弹-塑性状态判定

寒区隧道冻结围岩未进入屈服状态时,应采用其弹性力学模型,如图2 所示.相比寒区隧道塑性力学模型及其解答,此时冻结围岩完全弹性而不存在弹塑性分区,只剩r=r1处支护区与冻结围岩区交界、r=r2处冻结围岩区与未冻结围岩区交界,冻结围岩内缘r=r1处应力不满足MC 准则,其他求解思路同2.1 节.

图2 寒区隧道弹性力学模型Fig.2 Elastic mechanical model of a cold region tunnel

未冻结围岩区及支护区的应力和位移仍为式(3)～式(6),而冻结围岩区应力与位移表达式中的A1,A2变为

将式(21)分别代入式(9)和式(10),得弹性状态下寒区隧道冻结围岩区应力与位移的具体表达式.

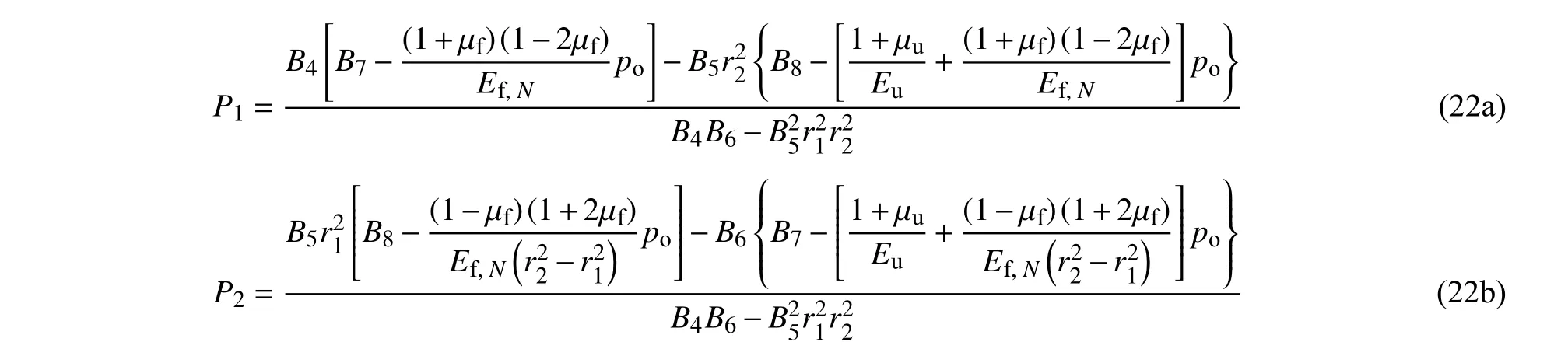
式中

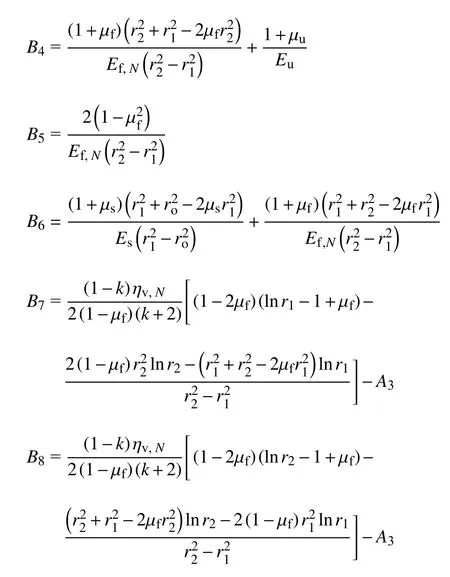
将式(22a)分别代入式(19)和式(20),得寒区隧道弹性状态下的洞壁位移ua与冻胀力ΔP1.

对于寒区隧道的弹-塑性状态判定,可将式(22)代入式(21),再将结果代入式(9)并令r=r1,得弹性状态下冻结围岩内缘处的应力,继而将其代入MC准则即式(11)进行判定:当σθf,e＜MNσrf,e+YN时冻结围岩保持弹性状态、无塑性区,否则进入屈服状态.也可通过冻结围岩塑性区半径rp与支护外半径r1的相对大小进行判断:当rp＜r1时冻结围岩保持弹性状态、无塑性区,否则进入屈服状态.

3 可比性及验证

本文综合考虑寒区隧道围岩不均匀冻胀属性和冻融循环对冻结围岩性能的劣化效应,采用MC 准则建立了寒区隧道冻胀力、应力与位移的塑性解答:式(20)为冻胀力解答,式(3)、式(4)、式(9)和式(12) 为应力解答,式(5)、式(6)、式(10) 和式(13)为位移解答,式(16)为塑性区半径的隐式计算方程,还给出了冻结围岩弹-塑性状态的判定方法,同时得到了寒区隧道的弹性解答,可为季冻区隧道设计提供一定的理论指导.所建立的寒区隧道MC 准则解答在一定条件下可退化为其他理论解.例如,系数k=1 时为各向均匀冻胀解答[4,17-18],次数N=0 对应不考虑冻融循环损伤的解答[3-5,7].因此,本文结果具有很好的可比性,可根据工程实际情况进行合理选择,具有重要的理论意义和应用价值.

Lü等[7]推导了不均匀冻胀寒区隧道的MC 准则解答,但未考虑冻融循环对围岩性能的劣化效应.当冻融次数N=0 时,本文结果退化为文献[7]解答.取表1 寒区隧道的塑性状态参数进行计算和对比,如图3 所示.可见,本文塑性解(N=0)与文献[7]的冻胀力、塑性区半径完全吻合,验证了本文退化结果的正确性.

表1 寒区隧道的塑性状态参数[7]Table 1 Plastic state parameters of a cold region tunnel[7]

图3 本文塑性解(N=0)与文献[7]解答的对比Fig.3 Comparisons between plastic results from this study with N=0 and Ref]7]

4 参数分析

对于未铺设保温层或防冻措施不佳的季冻区隧道,本文综合考虑短周期和季节性两类冻融[26],建议年冻融次数Na取2～ 3;对于铺设保温层、设置排水沟且实测温度表明防冻有效、围岩未经历冻融的寒区隧道,年冻融次数Na可谨慎地取0～ 1,并根据温度实测动态调整年冻融次数Na.探究冻融循环、不均匀冻胀以及体积冻胀率对寒区隧道应力分布、塑性区半径、洞壁位移和冻胀力等的影响规律具有工程实际意义.长期冻融循环对季冻区隧道安全造成不利影响,借助冻融次数N可量化冻融循环劣化效应;不均匀冻胀可通过不均匀冻胀系数k来体现;体积冻胀率ηv反映围岩的冻胀程度,受微裂纹密度ρo,微裂纹分布参数lc,水热迁移系数ζ和拟合参数s等的直接或间接影响.采用表2 所示寒区隧道参数进行本节的计算和分析.

表2 寒区隧道参数[13,18]Table 2 Parameters of a cold region tunnel[13,18]

4.1 冻融循环

当系数k=1.5 时,由节2.2 知冻结围岩内缘在冻融次数N=29～ 30 之间进入屈服状态,即N≤29 时冻结围岩处于弹性状态、N≥30 时冻结围岩处于塑性状态.弹性状态下N=0,15,29 时寒区隧道的应力分布如图4(a) 所示,图中区域划分及应力标注以N=15 时为例;塑性状态下N=45,60,75 时寒区隧道的应力分布如图4(b)所示,图中区域划分及应力标注以N=60 时为例;冻融次数N对寒区隧道冻胀力和塑性区半径的影响如图4(c)所示,对隧道洞壁位移的影响如图4(d)所示.

图4 冻融循环的影响Fig.4 Influences of freeze-thaw cycles

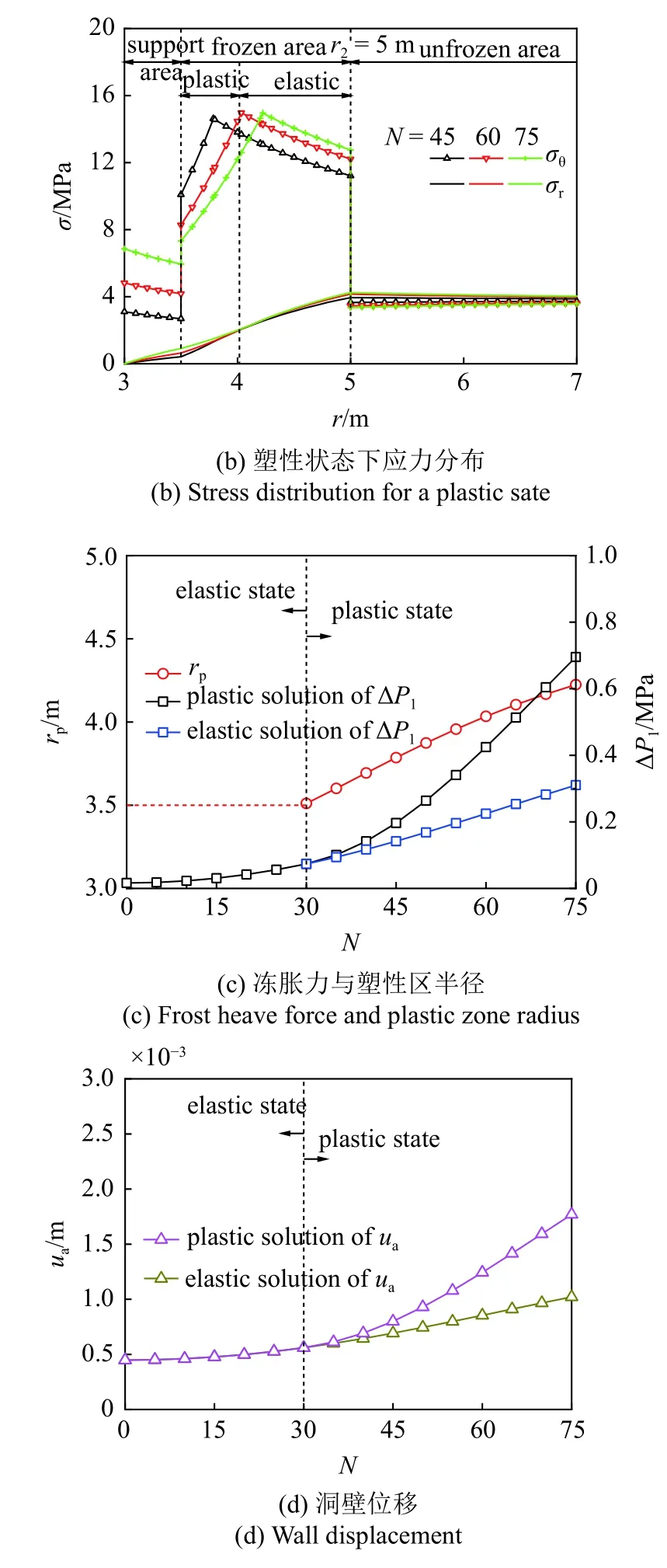
图4 冻融循环的影响(续)Fig.4 Influences of freeze-thaw cycles (continued)

由图4(a),图4(b)可知,随着冻融次数N的增加,径向正应力σr逐渐增大,切向正应力σθ在支护区和弹性状态下冻结围岩区呈递增趋势,而在未冻结围岩区和塑性状态下冻结围岩区逐渐减小,弹-塑性交界面处切向正应力σθ的峰值有所增大;冻结围岩内外缘处的切向正应力σθ均出现跳跃,这是由于内缘处冻结围岩与混凝土支护、外缘处冻结围岩与未冻结围岩的材料参数不同.

由图4(c)和图4(d)可知,塑性区半径、冻胀力及洞壁位移均随冻融次数N的增加而增大,且系数k=1,3 时的变化趋势一致.当N从30 增加至75 时,塑性区半径由3.51 m 扩大至4.43 m 而增大了20.3%,冻胀力塑性解增大了8.44 倍,洞壁位移塑性解增大了2.16 倍.这些都说明冻融循环对寒区隧道安全具有非常不利的影响,季冻区隧道工程设计时需重视并量化冻融循环导致的冻结围岩性能劣化效应,采取良好的防排水和防冻措施.另外,N越大弹性解与塑性解的差异就越大,故面对复杂多变的寒区地质条件宜采用本文塑性解答.

4.2 不均匀冻胀

结合节2.2 中冻结围岩弹-塑性状态的判别方法,当冻融次数N=60 时,无论不均匀冻胀系数k在[1,3]区间内取何值,冻结围岩都会进入屈服状态.冻胀力与塑性区半径随系数k的变化,如图5 所示.

由图5 可知,当k从1 增加到3 时,冻胀力增大了42.8%,塑性区半径仅减小了0.01 m,这表明围岩不均匀冻胀仅在很少程度上限制了隧道塑性区的发展,但冻胀力随围岩不均匀冻胀程度的增加而明显增大,冻融次数N=70,80 时冻胀力和塑性区半径的变化规律相同,应考虑围岩不均匀冻胀对寒区隧道冻胀力的显著影响,采取一定保温防冻措施既能减轻围岩冻融循环劣化又会降低隧道径向主冻胀危害.

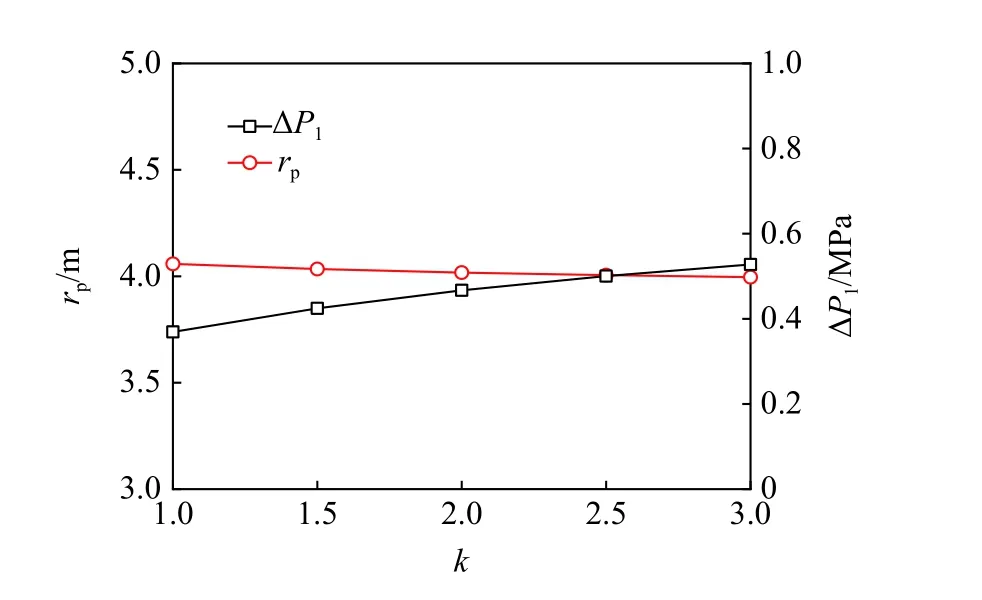
图5 不均匀冻胀的影响Fig.5 Influences of the non-uniform frost heave

4.3 体积冻胀率

微裂纹密度ρo、微裂纹分布参数lc、水热迁移系数ζ以及拟合参数s通过体积冻胀率ηv对寒区隧道冻胀力、塑性区半径的影响,如图6 所示,其中N=60,k=1.5.

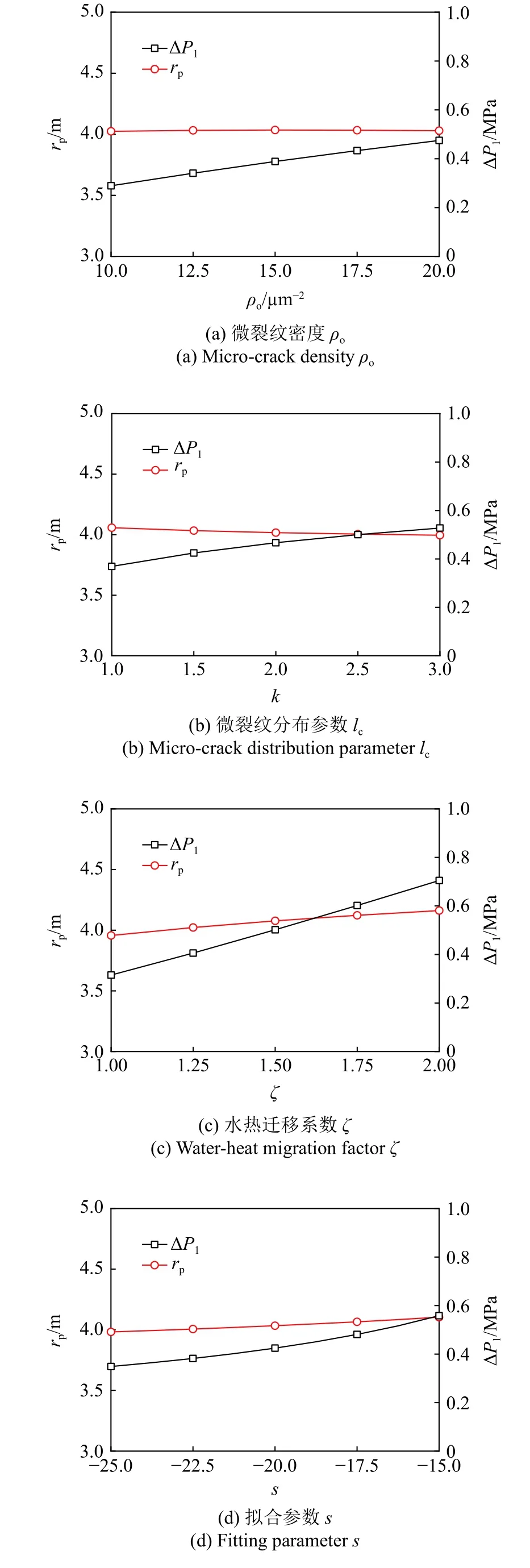
图6 体积冻胀率的影响Fig.6 Influences of the volumetric frost heave ratio

由图6 可知,4 种体积冻胀率参数对冻胀力和塑性区半径的影响趋势相似,且塑性区半径的变化均不明显.当微裂纹密度ρo由10 μm-2增加到20 μm-2、微裂纹分布参数lc由0.5 μm 增加到0.6 μm、水热迁移系数ζ由1 增至2、拟合参数s由-25 增加到-15 时,冻胀力分别增大了64.2%,33.6%,123.6%和60.1%,可见水热迁移系数ζ的影响最明显,即冻胀敏感性围岩的冻害程度最大.因此,应结合岩石冻融循环实测数据和CT 技术对体积冻胀率相关参数进行针对性测定或拟合取值,以保证季冻区隧道冻胀力计算的有效性.

5 结论

(1) 所建立的寒区隧道塑性解答合理考虑了冻融循环引起的围岩性能劣化与围岩冻胀的不均匀性,具有很好的可比性且得到文献[7]塑性解答的退化验证,可为季冻区隧道工程设计提供理论参考.

(2) 冻胀力和洞壁位移的塑性解答相比弹性解答大的多,受冻融次数的影响也更显著.季冻区隧道围岩由于长期冻融循环的性能劣化效应易进入屈服,采用塑性解答更能反映隧道的实际服役性态.

(3) 冻胀力、塑性区半径和洞壁位移均随冻融次数增加而增大,其中冻胀力增大达8 倍之多;冻胀力与围岩不均匀冻胀程度成正比,4 种体积冻胀率参数特别是水热迁移系数对冻胀力的影响显著.

需指出的是,本文寒区隧道塑性解答是在诸多假定下构建和验证的,可在以下4 个方面进一步完善:①依据塑性区与冻结围岩区的相对大小,提出塑性区超过冻结围岩区而扩大至未冻结围岩区[27]或冻结围岩区、未冻结围岩区同时部分屈服的力学模型,并考虑支护区混凝土的冻融损伤;② 确定不均匀冻胀系数与微观裂隙走向、形状、长度以及冻结区水分不均匀分布的几何定量表达式[28-29],且反映宏观裂隙开裂拓展引发的围岩劣化、导水通道贯通等,对体积冻胀率亦然;③表征冻结温度对冻结区范围、冻结围岩强度、体积冻胀率的综合作用[30],以分析冻结温度对寒区隧道应力分布、塑性区半径、洞壁位移和冻胀力的影响特性;④ 囿于应用本文寒区隧道塑性解答要由岩石冻融循环试验和CT 技术测定或拟合体积冻胀率细观参数以及围岩强度劣化规律,暂未查询到可供对比的寒区隧道模型试验、现场实测或数值模拟数据,结合具体寒区岩体工程有针对性地开展隧道现场监测与模型试验、岩石冻融循环试验,持续优化参数数目及确定方法,对所建立的寒区隧道塑性解答进行充分性验证及工程实践推广.