中性线修正型变截面梁类构件压电控制1)

于香杰 * 游斌弟 魏 承 * 赵 阳 * 夏 斌 刘朝旭 *

* (哈尔滨工业大学航天学院,哈尔滨 150001)

† (哈尔滨工业大学(威海)海洋工程学院,山东威海 264200)

引言

近年来,随着在轨航天器轻量化设计的提出,具备低质量特性的异性复合材料及变截面质量优化方式逐步被应用于各类航天器构件的设计中,形成复合变截面柔性航天构件[1].变截面梁是根据大型梁类航天构件的不同边界条件及结构应力差异对其质量进行重新分配所形成的典型变截面结构,该方式可有效增加航天器有效载荷重量,提高航天运载效率.然而,大型梁类构件通过变截面质量优化方式来提高工作能力的同时,不可避免的会引起系统整体结构刚度降低、模态阻尼减小[2],使其结构振动控制更为复杂化[3].此类振动将耦合热辐射环境、结构非线性及运动状态等因素发生非线性扰动[4],该类扰动在空间微重力环境下易激发系统非收敛式振动,甚至引起航天器系统失效[5].

Thornton 和Kim[6]通过建立太阳帆悬臂结构在热载荷下的动态响应规律曲线成功预测了哈勃太空望远镜悬臂结构的非线性热致响应,以此验证空间热载荷对航天系统工作精度的重要影响.郭红军等[7]采用有限元法分析了阶梯式变截面桅杆在不同太阳热流方向下的固有频率及振型.张弛等[8]和王琳杰等[9]均对航天器结构属性与空间热载荷间的耦合规律进行总结分析,指出机-热系统中复杂的非线性耦合影响关系难以通过准确关系式进行表述.张军徽等[10]通过对太阳帆桅杆在轨交替热响应分析得出,仅通过提高桅杆壁厚无法缓解热致变形影响.上述文献分析结果均指出空间热载荷易激励航天器构件柔性变形及非线性振动,且难以通过被动控制方式对其变形进行抑制.同时,多数研究[11]均基于小变形假设,难以准确预测大变形状态下变截面梁类构件的变形及应变状态.

Shabana[12]于1997 年首次提出了绝对节点坐标法(ANCF),该方法通过绝对节点来表征有限单元的变形状态,可避免科氏加速度所引起的非线性附加项,从而提高大变形条件下变截面梁构件动态行为建模效率与精度.Shen[13]通过ANCF 建立了在轨柔性展开机械臂热动力学行为响应分析,其数值分析结果可有效预测热冲击作用下航天构件变形响应.Yoo 等[14]采用ANCF 建立了端部附加质量的连续变截面桅杆动力学方程,并利用高速摄像机获取了变截面桅杆的变形数据,验证了ANCF 求解大变形运动的有效性和准确性.刘铖等[15]利用第一类Piola-Kirchhoff 应力张量的方法推导了高效ANCF应变计算方法.传统ANCF 建立变截面梁类构件位移场的过程中,多以结构中性线变形状态作为参考基础[16-17],通过分析参考点与中性线间的位置关系来实现任意点的变形预测.然而在传统分析过程中,变截面梁类构件的中性线均被假设与结构几何中位线重合,忽略结构非线性及材料各项异性对构件中性线的偏差影响,由此难以准确描述参考点处的应变状态.

同时,随着智能材料及其附属结构的提出,采取主动抑振措施来降低结构振动已成为提高航天构件在轨工作性能的重要举措[18-20].压电材料鉴于其特有的正逆压电效应,不仅可根据外部构件变化调整自身传感及作动能力,同时还具备高灵敏度、高动态性、易加工、附重小以及频带宽等动态优势性能,因而被广泛应用于柔性航天器构件的智能抑振抑变结构中[21-23].

Alfredo 和Sergio[24]及Erturk 和Inman[25]分别建立了Euler-Bernoulli 梁下压电效应的解析算法模型,从而精确预测参考点处的变形状态.Azimi 等[26]利用拉格朗日公式分析验证了锆钛酸铅型压电片(PZT)在航天器回转过程中对柔性附件的变形及振动抑制能力,之后并成功将其应用于航天器姿态控制组件之中.Fazelzadeh 和Azadi[27]分别采用压电材料作为智能卫星系统的传感及作动结构,并利用拉格朗日-瑞利-里兹方法建立了航天系统在热冲击作用下的非线性控制方程,成功验证压电智能材料对柔性构件热致振动的抑制能力.Li 和Shi[28]及Zhang 等[29]分别通过微分求积技术及PID 控制对压电结构的自由振动和强迫振动进行抑制.上述文献均依靠于传感型压电片获取参考点处的应变状态,并利用相应控制算法获取作动型压电片的驱动控制电压,以实现主动抑振控制系统的搭建.

依据文献分析可知,精确描述压电参考点处的应变是实现航天器柔性构件主动控制的重要前提.然而目前变截面梁构件在建模过程中存在中性线等效及小变形假设等问题难以实现准确应变描述.针对于此类问题,本文采用ANCF 与负应变率控制策略,研究了变截面梁类构件在几何结构及材料属性影响下的中性线偏移问题,并依靠修正化模型完成变截面桅杆算例下的压电铺层控制优化及增益系数分析等工作,以期为变截面梁类构件在轨抑振抑变控制提供参考数据.

1 复合变截面梁类构件动力学方程建立

1.1 复合变截面梁单元空间位置描述

带有压电层的复合变截面梁类构件整体示意如图1 所示,变截面梁沿x轴方向的截面呈非线性变化,其中f1(x)和f2(x) 分别为变截面梁在oxy投影面的上边界曲线及下边界曲线,梁的宽度为b(x),整体长度为l,均为关于x的函数.其中压电层分为作动型压电层与传感型压电层,根据不同控制策略,两种压电层分别安装于变截面梁的上下表面.

图1 变截面梁构件结构示意图Fig.1 Structure of beam with variable cross-section

离散后的变截面梁单元如图2 所示,变截面梁单元的长度li、宽度b(x)、厚度h=f1(x)-f2(x)+hp、压电层厚度hp均如图所示.任意变截面梁单元均具备两个独立节点(如图2 中A和B所示),其位置矢量在绝对坐标系下分别为 (0,0,0) 和 (li,0,0) 处,在全局坐标系下的位置矢量分别表示为rA和rB.如图2所示,变截面梁上任意点P在全局坐标系下的空间位置矢量可写为

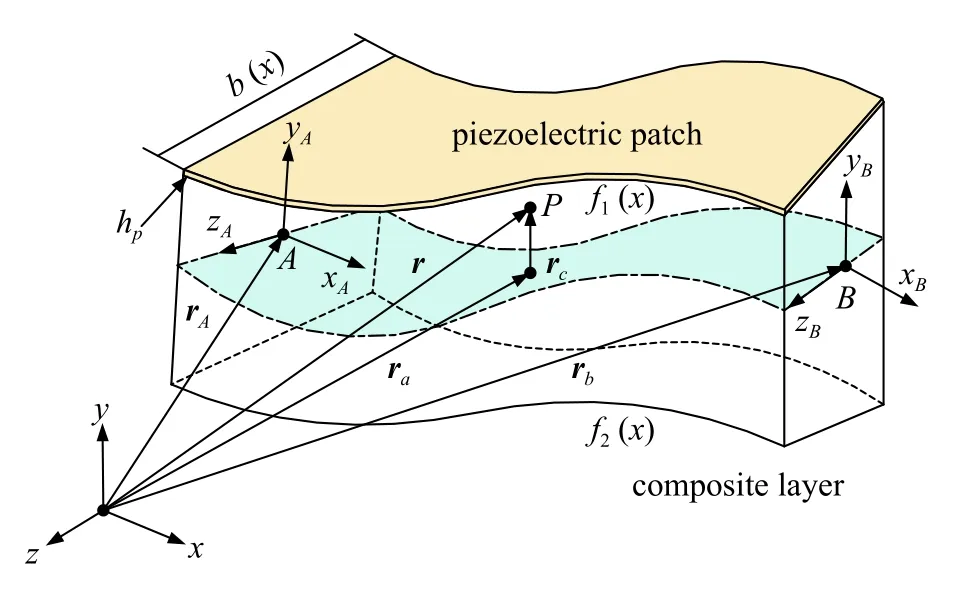
图2 变截面梁单元及空间位置描述Fig.2 Position description for beam element with variable cross-section

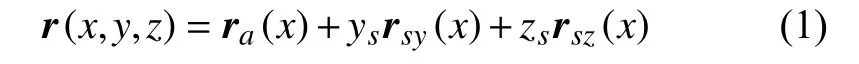
式中,ra为中性层上点的位置矢量,rsy和rsz分别为任意点P与中性层间沿y和z方向的方向矢量,ys和zs是任意点沿y和z方向与中性层间的距离.

传统ANCF 建模方法中均将中性层位置假设为几何结构中位面处,然而在变截面几何因素及复合材料各项异性的作用下,单元中性层与几何结构中位面不再重合,因此若仍以几何结构中位面为应变参考将会引起预测精度降低.为精确描述变截面梁单元中性层的位置,结合变截面几何结构及应力偏差[30]影响,论文将通过引入中性层偏差值对实际中性层进行修正

根据式(2),变截面梁单元的中性层投影曲线函数可表示

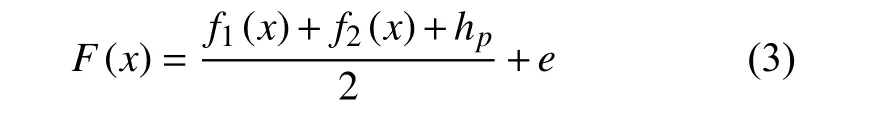
根据ANCF 特性可知,变截面梁单元的两个节点处分别具有12 个自由度,即变截面梁单元共具有24 个自由度,将两端点的自由度整理为矩阵形式

式中,qA和qB为A,B点在绝对坐标系下的位置矢量;表示节点斜率矢量,具体可写为

根据 Hermite 插值函数,式 (1) 可改写为

同理根据ANCF,任一点的位置矢量可通过形函数与节点坐标组合表示,因此引入形函数矩阵如式(6)所示

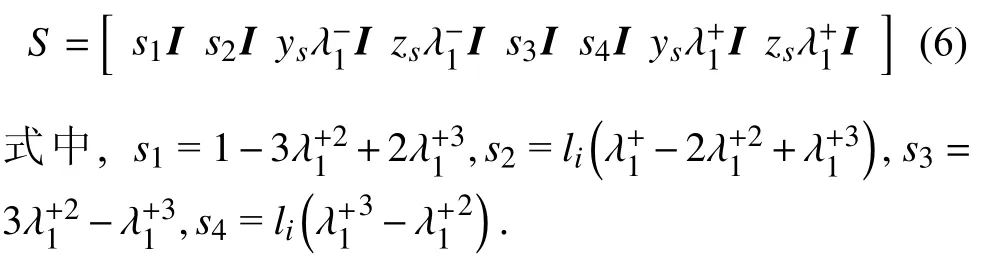
根据式(4)及式(6),变截面梁单元上任意点的空间位置可表示为

根据雅克比矩阵定义变截面梁上任意点的应变梯度为J,具体表示为

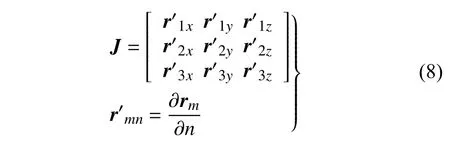
根据Green-Lagrange 应变张量公式,变截面梁单元的应变矩阵可表示为

对式(9)进行进一步运算,可得到公式的矩阵形式为

式中各项可表示为

将变截面梁单元的应变矩阵重组为列向量形式,式(10)可写为

根据式(11)及压电效应,变截面梁单元的非线性本构关系可表示为

式中,e1和e2分别为是正逆压电系数矩阵,μ 是介电常数矩阵,σE是电位移应变,k分别表示复合材料层及压电层,Qk是材料弹性矩阵,其通过材料弹性模量及泊松比确定,E为压电片两极板之间的电势差.

1.2 负应变率压电控制策略

为达到变截面梁单元最佳抑振效果,压电驱动电压应跟随变截面梁应变情况进行自适应调整,为此本文提出适用于ANCF 的负应变率控制策略.负应变率控制策略是以参考点应变作为输入变量的控制方法,根据式(11)所述,变截面梁单元任意点应变可表示为 ε,由于压电片的自感电压不受剪切应变影响,因此为便于计算可仅取应变矢量中的前3 项作为参考点输入应变,记为 εP.

引入G作为协调增益系数将应变信号调理为闭环电压信号,闭环电压信号可通过式(13)所述获得

结合式(10)和式(13)可改写为

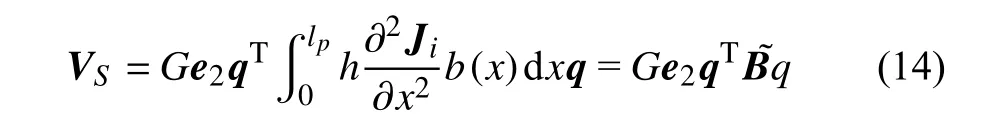
式中,i=x,y,z.

通过式(14)所获得的传感电压需再次结合增益调节系数转换为作动型压电片的工作电压,由此作用于压电片上的电压最终可表示为

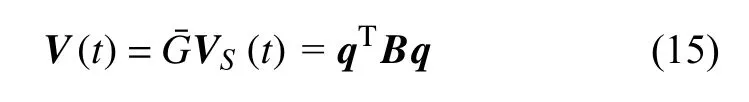
根据式(15)可知压电层沿x,y,z方向上任意点处的电场强度可表示为

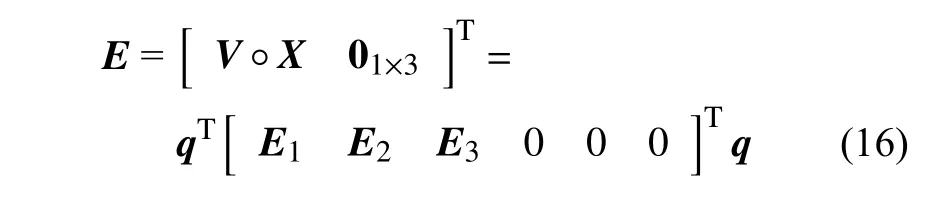
1.3 复合变截面梁单元动力学方程建立

根据式(7)可知变截面梁单元上任意点的空间位置矢量可为r(x,y,z),其中形函数矩阵为仅关于x,y,z的函数矩阵,节点矢量为时间t的函数矢量,因此变截面梁单元上任意点对时间的一阶导数可表示为,即任意点速度为

根据动能定理,任意变截面单元在运动过程中的单元整体动能可表示为

式中积分项表示单元体积,根据变截面梁单元的非线性几何关系可知,单元整体动能可进一步表示为

根据虚功原理对公式(19)进行变分,可得到

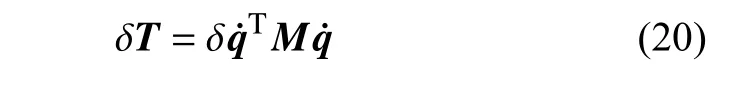
式中,M为变截面梁单元质量矩阵,该矩阵为常数矩阵.

进一步通过虚功原理对变截面梁单元的应变能矩阵进行变分,可得到变截面梁单元的应变虚功方程为

进一步整理后,式(21)可表达为

式中K为变截面梁单元的刚度矩阵,分别通过以下5 项确定

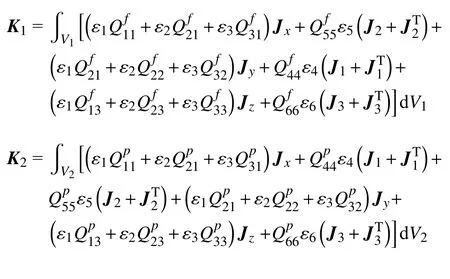
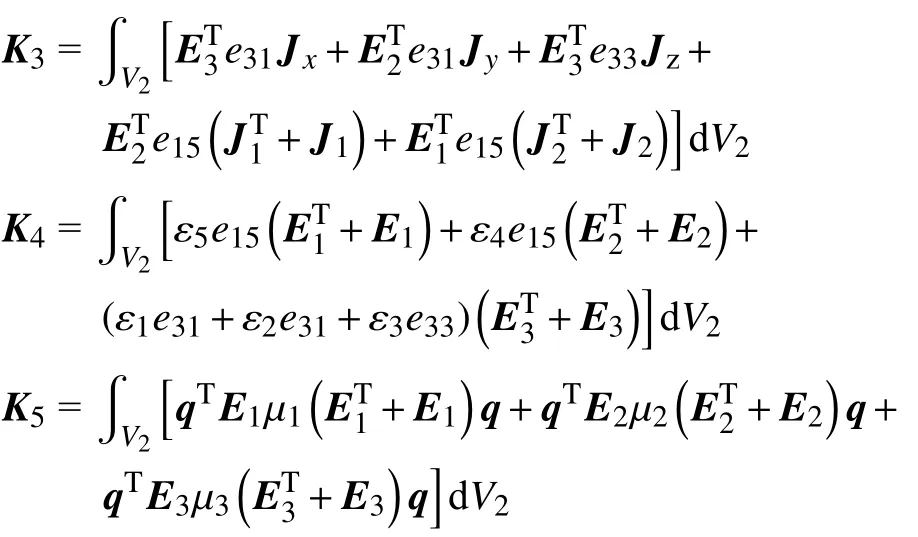
式中,V1和V2分别为变截面梁单元复合层及压电层的体积,eij为压电系数矩阵对应项,μi为介电常数矩阵对应项,分别为变截面梁单元复合层及压电层所对应柔度系数.

为降低在轨工作过程中热致振动对变截面梁构件的动态行为影响,需探究热辐射因素与变截面梁间的耦合机理,设定变截面梁单元在轨运行过程中所受到的空间热辐射矢量为

式中,θ和 α 分别为空间热流Q与绝对坐标系y,z方向的夹角.

由于压电层的厚度较小,且压电材料的热稳定较高,因此可忽略压电层热致响应的影响,变截面梁单元在该热辐射作用下的温度场分布可表示为

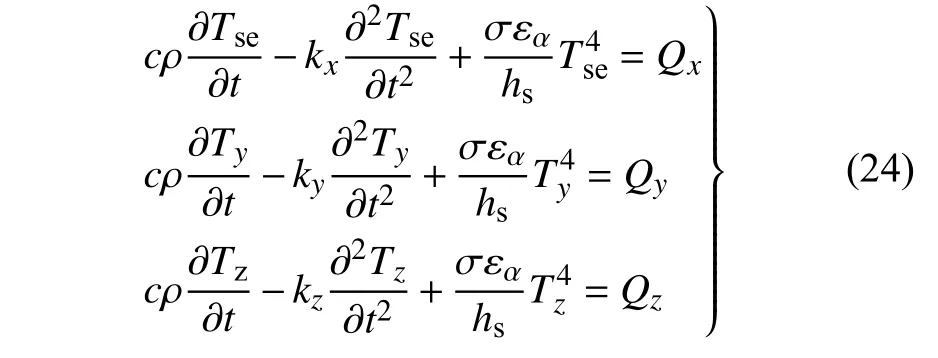
式中,c为复合材料热容,ρ 为复合材料密度,ki为复合材料沿i方向的导热系数,σ 为Stefan-Boltzman常数,εα为复合材料辐射系数,hs为桅杆截面壁厚,Tse为截面摄动温度,Ti为i方向的平均温度.

根据热致响应原理,截面摄动温度主要引起轴向热载荷,截面平均温度主要引起热弯矩载荷,则根据任意节点处截面平均温度及截面摄动温度的分析可知,任意节点的轴向热载荷及热弯矩载荷分别可表示为

式中,αT为热膨胀系数.

利用虚功原理可以得到热弯矩和轴向热载荷引起的外力矩阵.由于轴向热载荷的作用方向为x轴,则轴向热载荷所引起的外力虚功为

式中,Qr为轴向热载荷所引起的外力矩阵.

假定热弯矩载荷My和Mz在变截面梁单元中引起xy和xz方向的微小转动分别为 θy和 θz,则热弯矩对应虚功可表示为

其中,微小转动角 θy和 θz分别可根据xy截面和xz截面的几何关系确定,其具体可分别表示为

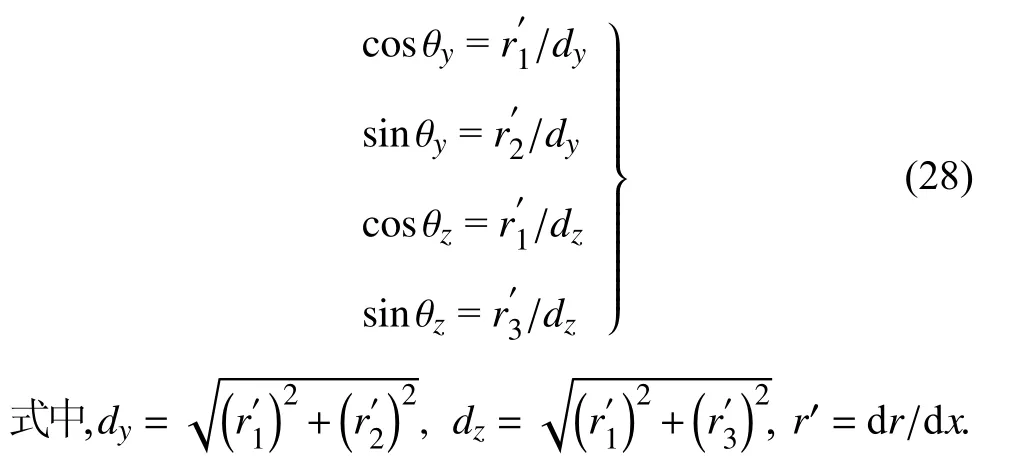
结合式(7)和式(27)可进一步写为

因此,变截面梁单元任意节点处沿zx平面及xy平面热弯矩载荷所引起的外力矩阵可表示为

通过布尔矩阵将变截面梁构件上所有节点处的外力矩阵进行整合,则变截面梁构件系统外力矩阵可表示为

式中,B1为布尔转换矩阵,Qs为变截面梁单元节点总合外力矩阵,具体可表示为Q=Qr+Qy+Qz.

结合式(20)、式(22)及式(31),变截面梁单元在考虑压电效应及空间热致响应耦合作用影响下的动力学方程可表示为

2 算例数值结果

2.1 模型验证

太阳帆桅杆作为一种典型的大型柔性变截面梁类构件,文献[10,31-32]均对其在空间热辐射作用下的热致动态响应进行了分析,但少有文献采用压电智能材料对其柔性变形及振动进行主动控制.为验证本文所提出ANCF 修正模型的准确性并揭示变截面梁类构件在机-电-热耦合作用下的动态行为响应规律,从而实现太阳帆桅杆在热辐射作用下的压电主动抑振控制,本节将以变截面太阳帆桅杆为研究对象,通过所述模型对其在轨实际工作过程进行数值分析.

本文所采用的变截面太阳帆桅杆如图3 所示,太阳帆桅杆共被分割为4 个变截面ANCF 单元.由于桅杆悬臂端末端点的整体变形较大,便于构件动态性能观察,因此以变截面太阳帆桅杆末端处的点P作为变形及应变参考点.作动型压电片根据不同分析策略安装于各变截面桅杆的上表面.

图3 二次型变截面太阳帆桅杆结构示意图Fig.3 Structure of solar-sail masts with parabolic section

变截面桅杆及压电片材料参数如表1 所示.

表1 桅杆碳纤维材料及MFC 材料属性参数Table 1 Material properties of carbon fiber and MFC

根据式(1)对中性层偏差修正模型描述可知,变截面太阳帆桅杆受其几何结构因素及材料各项异性等特点影响,其中性线不与几何中位线重合.结合压电层在变截面太阳帆桅杆上的实际安装位置,压电应变参考点P位于变截面桅杆单元的边线处.分别采用中性线修正方式以及传统中位线等效方式对变截面梁构件进行动力学预测,仿真输入参数分别如图4 和表1 所示,仿真时长为40.0 s,步长为0.01 s.点P在不同模型描述下的变形历程曲线如图5所示,为验证模型正确性,本文对比了该模型在ABAQUS 软件下的仿真结果.根据图5 所示,模型数值结果与ABAQUS 仿真结果具有较高一致性,因此可验证模型的计算合理性.由于修正后的中位线更接近于点P的位置,因此修正模型的变形仿真结果相较于原模型的结果略有减小,因此可证明修正模型更精确地描述参考点随时间的应变规律及空间相对位置状态.

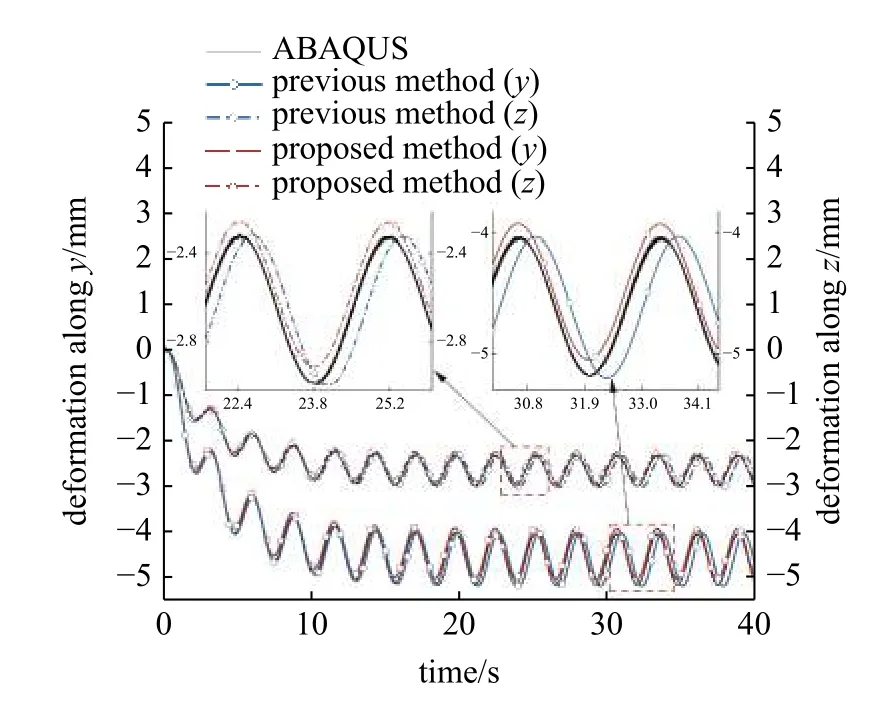
图4 不同模型下参考点P变形Fig.4 Deformation of Pwith different methods

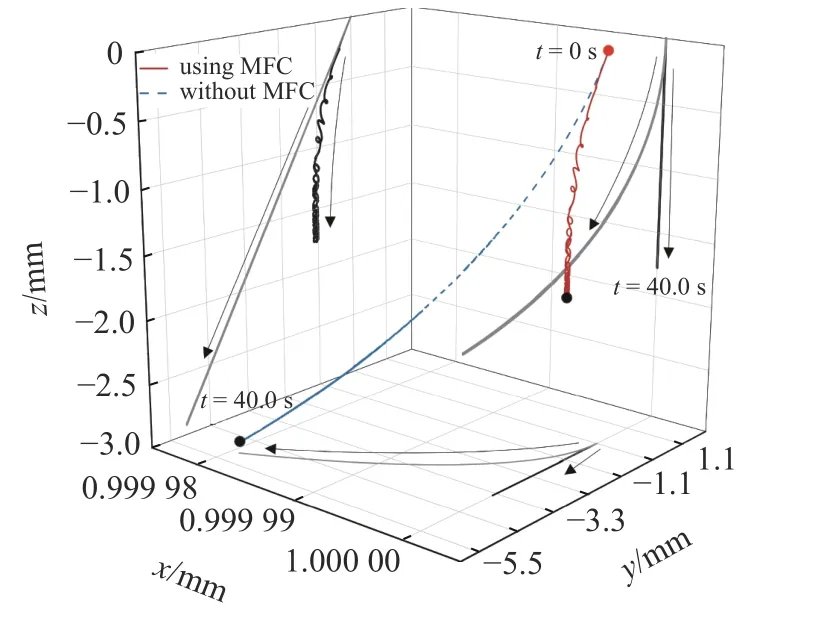
图5 点P空间位置时间历程曲线Fig.5 The position of point P

根据负应变率控制策略及式(14)可知,作动型压电片的驱动电压取决于传感式压电片参考点应变及调节增益系数,因此准确描述传感式压电片参考点应变是实现压电主动抑振控制技术的重要前提.在数值分析过程中,以作动型压电片安装于4 号变截面桅杆单元为例,根据式(11)所述应变场模型来捕获点P处的应变规律,并将应变信息输入至负应变率控制模型,当调节增益系数取0.03 时,点P在空间范围内的时间历程曲线如图5 所示.根据图示可知,在变截面太阳帆桅杆加入压电主动控制策略之后,点P的弹性变形得到有效抑制.根据点P在xy面的投影可知,点P在xy投影面及xz投影面均呈现直线状态,因此点P在x方向上几乎不发生变形;由于变截面桅杆沿y,z方向存在材料异性、几何结构及外力干扰等因素差异,点P在y,z方向上的应变呈现非线性同步,从而使得沿y,z方向的负应变率控制电压呈现非同步性输出,表现为点P在yz投影面上呈现非规则螺旋型下降状态.

2.2 压电铺层安装位置影响分析

上述分析均在负应变率压电控制机理层面进行讨论,然而为获得变截面太阳帆桅杆在空间热载荷作用下的最佳抑振抑变控制策略,需综合考虑作动型压电片的安装位置及式(15)中所述调节增益系数对变截面太阳帆桅杆运动状态的影响.当调节增益系数为固定值时,在不同数目及安装位置作用下,变截面太阳帆桅杆的最大应变状态如图6 所示.由图可知,不同作动型压电片的安装位置及数目对变截面太阳帆桅杆的最大变形状态具有显著影响.根据整体曲线对比可得,在变截面桅杆各单元均安装作动型压电片时(1-2-3-4),变截面太阳帆桅杆的整体变形较大.其原因为压电传感应变参考单元为4 号单元,各变截面桅杆单元间应变状态存在一定差异,因此使得控制过程中其他单元的电压输入量存在不同程度的超调与方向漂移,从而使得各作动型压电片之间的协调控制同步性能降低,最终导致抑振抑变效果削弱.

图6 变截面太阳帆桅杆在不同数目及安装位置下的最大应变状态Fig.6 The maximum deformation of solar sail mast with different assembling position of MFC

根据图6(b)和图6(c)对比可知,当1 号变截面桅杆单元安装有作动型压电片时,其沿y和z方向的变形量均大于其他压电控制方案,末端变形量分别达到了4.96 mm 与2.85 mm.同理,当仅有1，2 和3 号变截面梁单元组合控制时,1 号变截面梁单元处的作动型压电片为主要作用源,对比最小应变状态可知,其对变形抑制效果均产生削弱作用.对比图6(d)可知,当仅有4 号变截面桅杆单元采用作动型压电片时,其变形状态得到最佳抑制效果.其原因在于,传感型压电片被安装于4 号变截面桅杆单元,各作动型压电片输入电压均以4 号单元应变为控制参照,随着各作动单元与应变参考单元间的距离增加,其应变同步性逐步降低,因此使得各单元间的压电作动应变难以完全协同变截面太阳帆桅杆运动过程中的柔性应变.同时根据悬臂梁的特殊性质可知,相较于在悬臂端施加应力,固定端施加应力会伴有放大效应,从而对变截面太阳帆桅杆末端的变形状态产生更大影响,因此在压电控制过程中,靠近于固定端的作动型压电片将起主要影响.综上所述,当调节增益系数固定不变时,随作动单元与应变参考单元间的距离增加,应变协调同步性会随之降低,从而削弱压电控制效果;同时由于变形抑制过程中悬臂梁固定端所具有的放大效应,变截面太阳帆桅杆的最终变形抑制效果取决于靠近悬臂梁固定端的作动型压电片.

2.3 压电增益调节系数影响分析

增益调节系数在前述分析中均固定为0.03,由于增益调节系数的改变将直接作用于作动型压电片的驱动电压,因此论文将一步针对增益调节系数对抑振抑变效果的影响进行分析.

当作动型压电片采用1-2-3-4 排布方案,y和z方向的增益调节系数分别设定为0.03 与0.05 时,点P沿y和z方向的时间历程曲线如图7 所示.由图可知,相较于未施加压电控制,点P在运动过程中各方向的柔性变形及振动均得到了有效抑制.根据式(25)分析可得,作用于变截面桅杆单元y和z方向上的载荷大小存在差异,为综合比较不同增益调节系数对压电抑振效果的影响,本文引入变形抑制率作为无量纲化对比指标,定义抑制率η

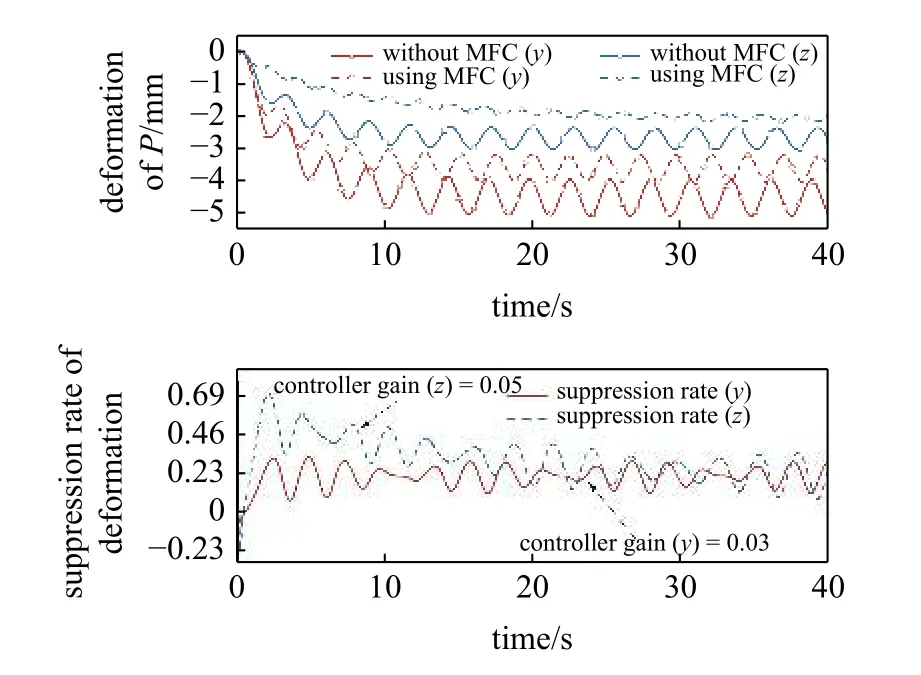
图7 不同增益调节系数影响对比Fig.7 Deformation of Pwith different controller gain

式中,pi为未施加压电控制下点P的柔性变形大小,pz为施加压电控制下点P的柔性变形大小.

点P在时间历程下的抑制率动态曲线如图7 所示.由图可知,由于变截面桅杆单元在z方向的增益调节系数大于y方向,因此在压电控制作用下,变截面桅杆单元沿z方向的变形抑制率总体高于y方向.同时在0～ 10.0 s 非稳定变形阶段,z方向的变形抑制率整体较高,其主要原因为该阶受非稳定性外力影响较大,从而使得变截面桅杆单元应变波动显著,因此可说明放大增益调节系数可增加作动型压电片对单元应变的敏感程度,从而提高系统整体抑振抑变能力;点P在20.0 s 后趋于稳定振荡阶段时,z方向的最大变形抑振率接近于y方向,但沿z方向抑振率的变化幅值远小于y方向,因此可说明放大增益调节系数也可进一步提高压电控制效果稳定性,从而优化变截面太阳帆桅杆在运动过程中的动态行为参数.

为进一步验证增益调节系数在放大过程中对压电抑振抑变能力的影响,以增益调节系数为0.03 时,点P沿y方向在变形稳定阶段的数据为研究对象,绘制其庞加莱相图及截面图.其分析结果如图8 所示,当庞加莱截面允许误差在0.2 范围内时,庞加莱相图呈现规则圆形且庞加莱截面呈现有限的规律性散点,因此可证明在增益调节系数为0.03 时,当变截面太阳帆桅杆在稳定振动阶段(20.0 s 后),点P呈现周期性稳定振动,压电控制效应对系统整体稳定性具有正向作用.

图8 增益调节系数0.03 时稳定阶段庞加莱图Fig.8 The poincare map of Pwith 0.03 controller gain

当增益调节系数放大至0.1 时,点P在稳定振动阶段沿y方向变形的庞加莱相图及截面图如图9所示.根据图示所知,点P在稳定振动阶段的庞加莱相图呈现明显混沌现象,同时,其在一定周期内的庞加莱截面图呈现非规律性散点,由此可说明在该增益调节系数作用下变截面太阳帆桅杆在20.0 s 后处于非周期性振动.综上所述,增益调节系数对变截面太阳帆桅杆的压电抑振抑变效应存在非线性影响,在一定程度内提高增益调节系数可实现变截面太阳帆桅杆压电控制稳定性及灵敏性提升;然而当增益调节系数发生超调时,将会激励变截面太阳帆桅杆产生附加非周期性振动,从而影响系统整体动态行为响应,降低压电抑振抑变控制效果.

图9 增益调节系数0.1 时稳定阶段庞加莱图Fig.9 The poincare map of Pwith 0.1 controller gain

3 总结

传统ANCF 建模过程中多以几何中位线对构件中性线进行等效,此类方法难以对单元位移场进行精确描述.针对此类问题,本文提出了一种用于精确描述非线性变截面梁类构件变形的ANCF 建模方法.该模型综合考虑构件变截面结构及微观材料属性对梁单元中性线的偏差影响,通过修正应变参考点与中性线间的相对位置关系.并深入结合负应变率控制法建立了变截面梁构件在空间热载荷作用下的压电抑振抑变结构,通过对应数值分析结果验证了该模型的准确性及精度.

根据本文所提出的ANCF 修正模型,以典型变截面太阳帆桅杆在轨实际工作为算例,深入研究在不同作动型压电片数目、安装位置及增益调节系数下变截面桅杆结构的动态行为规律.数值分析结果表示,靠近于传感式压电片处的作动环节具有较高的控制同步性,随作动型压电片与传感型压电片间的距离增加,作动单元与传感单元间应变描述非同步性提升,使得控制性能降低;其次,在一定范围内提高增益调节系数可增加控制系统的稳定性及灵敏性,但增益调节系数超调将会激励变截面桅杆产生非周期性振动,从而降低系统动态响应稳定性.