软体连续机械臂动力学建模与仿真1)

白争锋 孔清峰 赵 起

(哈尔滨工业大学(威海)机械工程系,山东威海 264209)

引言

软体机器人以其无限自由度、被动变形适应环境和柔顺接触等优势在医学、航天、农业、汽车、制造、核能、医疗保健和康复、环境保护和海洋勘探、反恐侦察等方面有着广阔的应用前景[1-3].在过去十多年中,软体机器人成为众多学者研究的对象.仿象鼻、章鱼触手等结构的机械臂式连续体机器人,以其固有的柔顺性,安全性及适应非结构化环境的优良特性使其显示出巨大的应用潜力,成为目前机器人领域的热门研究方向之一[4-8].

目前,研究人员针对软体机械臂进行了一系列的研究,并取得了一些研究成果.Walker 等[9-13]对软体机械臂建模做了大量研究,Renda 等[14]设计的仿章鱼软体机械臂样机,基于Cosserat 梁理论将软体机械臂轴线表示为空间中的一维曲线,并考虑了缆索驱动机器人的相关弹性力、驱动力和重力,建立了肌腱驱动的软体机械臂运动学及静力学模型;基于Kelvin-Voight 线性黏弹性本构方程建立Cosserat 应变模型[15],建立软体章鱼臂机器人在水下环境中的动力学模型;其后提出一种基于离散化Cosserat 理论的分段恒应变[16]方法,并建立了软体机械臂的运动学和动力学模型.然而该方法推导出的动力学方程是一组耦合偏微分方程,在数值求解上十分困难.Kang 等[17-19]利用章鱼生理解剖结构,基于分布式的弹簧-阻尼模型模拟章鱼臂4 个纵向和4 个径向肌肉,建立了章鱼机械臂的三维动力学模型,但是该模型没有从能量的角度考虑集中质量模型,并且使用欧拉递推法建立动力学方程,方程推导十分繁琐.Rone 和Ben-tzvi[20]使用一组有限的运动学变量来捕获机械臂的曲率变化,基于虚功原理为肌腱驱动的软体机械臂建立了动力学方程;在推导动力学方程中考虑了惯性、致动、摩擦、弹性和重力等效应.然而该方法推导连续臂的动力学方程会导致复杂的非线性积分,除了固有的数值不稳定性之外,这些积分在计算上是不可行的,因此该方法有一定的局限性.

Tatlicioglu 等[21]基于恒定曲率和分布式质量建立了可变长度连续体机械手平面动力学模型,并考虑了重力势能项和弹性势能项,使模型与机械臂的真实行为相一致.Falkenhahn 等[22-23]提出了一类称为仿生操作助手的连续机械手的动力学模型,该模型采用欧拉-拉格朗日方法,并基于分段常曲率假设,将每个段的质量看作集中质量放置在每段的末端位置.该模型虽然在数值计算上可行,但是将每段质量看作位于头部的集中质量并不能从能量上与实际的分布式质量相匹配.Giri 和Walker[24]建立了三段式平面软体机械臂动力学模型,然而该模型将每段的质量看作位于末端的集中质量.针对软体机器人变形后呈圆弧形状弯曲,Mazzolaii 等[25]提出分段常曲率(PCC)理论模型.对于变曲率弯曲问题,可将软体机器人本体结构分为多段,假设每段曲率恒定,每段形状可通过曲率半径、两截面所在平面间夹角以及两截面扭转角来描述[26-27],然后建立末端截面与坐标系的关系.

软体机械臂动力学模型数值求解精度与计算效率对于软体机械臂的动态控制至关重要.本文基于模态方法推导软体机械臂运动方程,明确地从能量的角度考虑软体机械臂动力学特性,提出一种基于质心集中质量的软体机械臂动力学模型,该模型将软体机械臂的分布质量等效为位于质心的集中质量,通过动能等效系数实现二者的动能匹配.与将集中质量放置在任意位置(例如,软体机械臂的末端)的集中质量模型相比,该模型兼顾了采用连续分布质量进行拉格朗日方法分析时的准确性,以及采用离散化的集中质量模型分析时的计算高效性.仿真结果表明,本文提出的将集中质量放置在与机械臂的能量行为相匹配的位置所建立的软体机械臂集中质量动力学模型,能够准确、高效地捕获软体机械臂的动力学特性,并且数值计算稳定.

1 运动学建模

1.1 软体机械臂模型抽象

将软体机械臂抽象为如图1 所示的结构,软体机械臂由三个结构完全相同的驱动器组成,且均布在间距为120°以r为半径的轻质圆形刚性框架上,刚性框架实现了三个驱动器在空间上隔离与固定.结构中也等间隔分布圆形刚性框架,以保持驱动器轴线方向始终平行于中性轴,假设刚性框架相对于驱动器的质量可以忽略不计.三个驱动器的初始长度均为 ℓ,各驱动器的总长度随时间变化规律为ℓ+ℓk(t),k∈{1,2,3},k表示软体机械臂上三个驱动器的编号,其中 ℓk(t) 表示各驱动器长度的变化量,并且驱动器长度的变化量在一定的范围内,即 ℓmin,ℓmax均为定值,其物理意义是驱动器的最大压缩量或最大伸长量.如图1(a)描述的是软体机械臂在空间中弯曲后的形状,软体机械臂在空间中弯曲成一段圆弧,C点表示圆弧的曲率中心,全局参考系 {R} 的原点O与软体机械臂下底面的中心重合,将驱动器1 的底端落在X轴正方向上的A点,驱动器2 和3 按逆时针方向布置,分别对应于B点和D点.

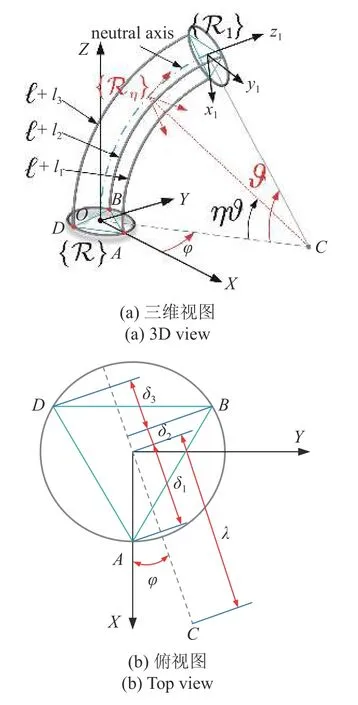
图1 空间软体机械臂示意图Fig.1 Schematic diagram of space soft manipulator

为了简化分析,在软体机械臂运动学建模时提出以下基本假设:

(1) 软体机械臂变形过程中,各驱动器假定为弯曲曲率相等的光滑连续曲线;

(2) 驱动器变形过程中不考虑扭转变形;

(3) 驱动器仅沿长度方向变化,径向尺寸不发生改变;

(4) 软体机械臂沿长度方向具有均匀面密度.

1.2 驱动空间到配置空间的映射

为描述软体机械臂的运动,引入如下坐标系:全局参考系 {R}固连在机械臂的底端,局部参考系{R1}固连在上端,并且z1轴与中性轴相切.根据假设(1),软体机械臂变形后在空间中的配置可以由一组曲线参数完全定义,曲率半径λ ∈(0,+∞),瞬时曲率中心C;弯曲张角ϑ,以及弯曲平面相对于X轴正方向的转角 φ∈[-π,π] .为了获得末端执行器的位姿与驱动器的长度变化量的关系,定义三个空间与两个映射.如图2 所示,三个空间分别为:代表驱动空间关节变量;代表配置空间关节变量;H代表局部参考系 {R1}到全局参考系{R}的齐次变换矩阵,x代表任务空间,即软体机械臂末端的笛卡尔空间.两个映射分别为:fspecific表示从驱动空间到配置空间的映射,即 κ=κ(q),fgeneral表示从配置空间到任务空间的映射,即H=H(κ) .根据文献[28]可以建立驱动空间到配置空间的映射关系为

图2 不同空间的运动学映射Fig.2 Kinematic mapping of different spaces

1.3 配置空间到任务空间的映射

考虑配置空间κ到任务空间x的映射关系,即求解局部参考系{R1}到全局参考系 {R} 的齐次变换矩阵H.齐次变换矩阵需要经过如图3 所示的5 个步骤得到,分别为:首先,绕全局坐标系 {R} 的Z轴旋转角度φ;然后沿着当前参考系X轴正向移动距离λ;接着绕当前参考系的Y轴旋转角度ϑ;再沿着当前参考系的X轴负方向移动距离λ;最后绕着当前参考系Z轴旋转角度-φ,最终得到配置空间到任务空间的齐次变换矩阵为

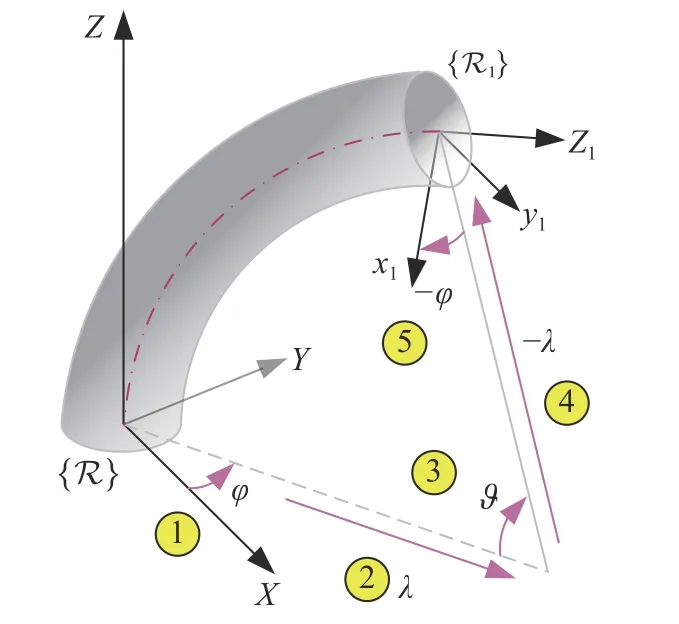
图3 齐次变换矩阵的生成步骤Fig.3 Steps of homogeneous transformation matrix

式中,Θ(κ)∈R3×3表示局部参考系 {R1} 到全局参考系{R}的旋转矩阵,ψ(κ)∈R3×1表示局部参考系{R1} 到全局参考系 {R} 的位置平移向量.

Ψ(κ,η)∈R3×1表示动参考系到全局参考系的位置平移向量,该向量中的3 个元素表达式如下

1.4 配置参数的局限性

式(3)给出的齐次变换矩阵包含关节空间中连续体中性轴上任意点的位置和方向,但该矩阵中的每个元素都是由三角函数构成.由于三角函数属于复杂的非线性函数,并且该式中使用的配置参数为λ和φ,这两项中的分母分别为和l2+l3-2l1,这将产生一个不可避免的问题,即当l1=l2=l3时,这两项的分母都将变为零,随之导致数值计算的奇异性与不稳定性.如果采取一种处理方式,将齐次变换矩阵中各元素近似为数值稳定的多元多项式,则可避免奇异性问题.不同类型的级数展开法,如幂级数、傅里叶级数以及泰勒级数均可用于简化复杂的非线性函数[29].考虑到软体机械臂连续变形的特性,多元泰勒级数展开不含三角项的多项式与具有驱动空间关节变量的分母,因此能够有效消除数值计算的奇异性与不稳定性.

本文在描述软体机械臂变形后的空间位置描时,使用模态方法代替配置参数导出的运动学方程,从而避免奇异性.模态方法是利用简单的多项式函数逼近复杂的非线性函数,同时,利用模态坐标将会极大提高动力学方程求解效率.鉴于此,将式(3)展开为三元泰勒级数,齐次变换矩阵H用模态齐次变换矩阵T近似表达,本文给出截断误差具有11 阶精度的模态变换矩阵的表达式,为表示方便,令

则模态变换矩阵T中模态旋转矩阵R的表达式如下

模态变换矩阵T中模态位置平移向量p的表达式如下

则软体连续臂中性轴上任意点到全局参考系的模态齐次变换矩阵为

基于泰勒级数的模态方法提供了一个直观和直接的选择,使齐次变换矩阵H中的每个元素产生唯一且精确的多项式函数,因此,它避免了模型转换和模型奇异性.此外,软体机器人正运动学和逆运动学都可以在空间关节中直接计算,而不需要额外的奇异性解决方法,并且所提出的方法可以简便地扩展到多节连续机械臂的动力学建模中.

2 连续机械臂动力学建模

通常认为机械臂的质量是沿臂的长度均匀连续分布的,如图4(a)所示.本节首先考虑机械臂的质量是沿臂的长度均匀连续分布的,基于拉格朗日方法建立软体机械臂动力学模型;然后提出基于质心集中质量的动力学模型,机械臂的质量位于质心处,如图4(b)所示.

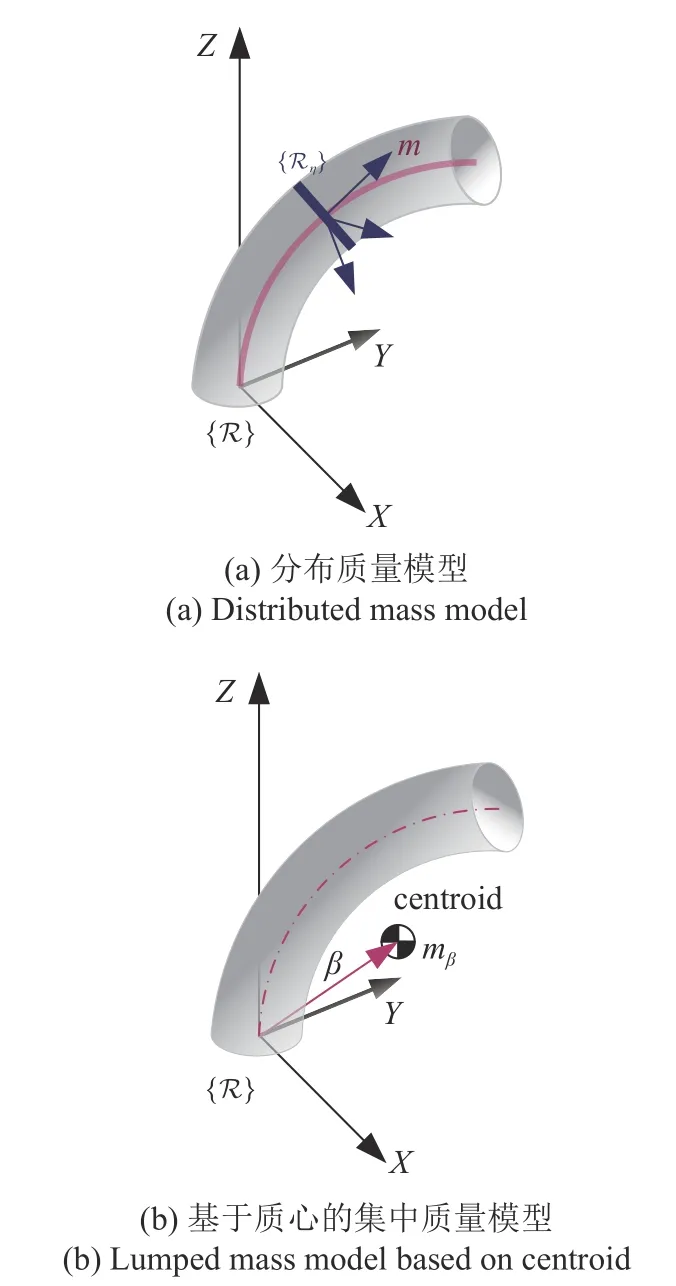
图4 两种动力学模型Fig.4 Two kinds of dynamics model

2.1 分布质量动力学建模

软体机械臂的拉格朗日函数可以写为 L=K-P,其中 K 表示软体机械臂的总动能,P 表示软体机械臂的总势能.总动能 K=Kυ+Kω,Kυ表示软体机械臂的平动动能,Kω表示软体机械臂的转动动能.总势能 P=Pg+Pe,Pg表示软体机械臂的重力势能,Pe表示软体机械臂的弹性势能.为获得以上各能量项的表达式,如图5 所示基于微分的思想将软体机械臂沿中性轴看作无穷多个切片组成,中性轴上η处切片的示意图如图6 所示,将切片看作质量为mdη,厚度为λϑdη,半径为r的均质圆盘.位于η处切片的动能与势能得到后,通过从底部到顶部对η从0 到1 积分确定软体机械臂的总能量.

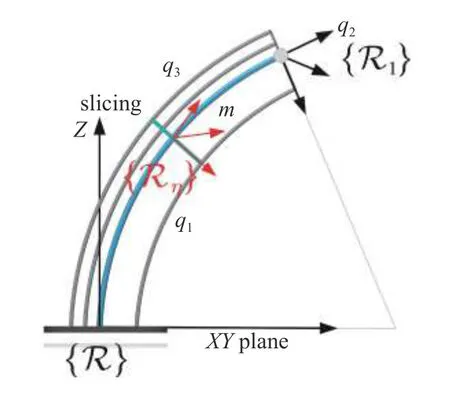
图5 切片示意图Fig.5 Schematic of slice

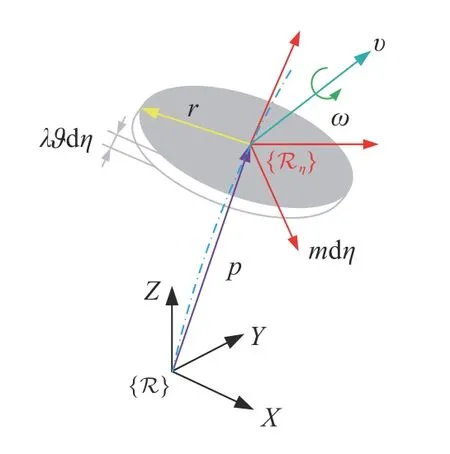
图6 切片放大示意图Fig.6 Slice enlargement

2.1.1 动能计算

为确定软体机械臂的总动能,采用式(9)推导的模态变换矩阵获得切片的瞬时速度,包括线速度ν与角速度ω.将式(8)对时间求导可得中性轴上任意点η处切片相对于全局参考系 {R} 的线速度为

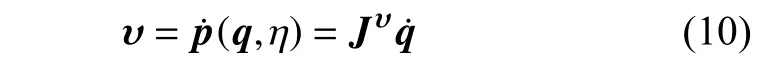
式中,线速度雅可比矩阵Jn表达式为

中性轴上点η处切片在体参考系 {R1} 中的角速度为

式中,操作符 ∨ 表示对反对称矩阵提取非零元素,且角速度的三个分量为

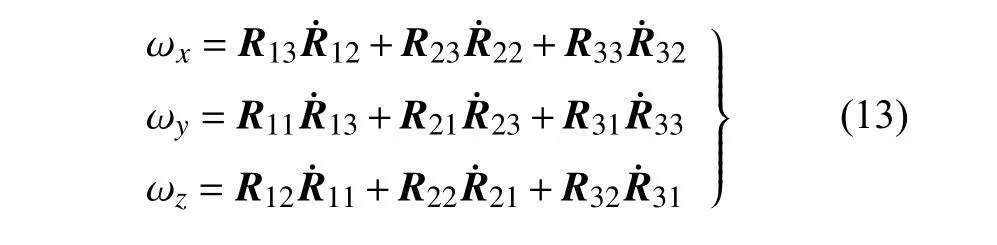
由于假定软体机械臂的质量恒定且具有均匀的面密度,因此切片质量mdη具有的线惯性矩阵为Mυ=mdηI3,I3为三阶单位矩阵.又由于假定切片具有圆形截面,因此其具有的惯性张量为Mω=Ixxdiag(1,1,2),其中表示对角矩阵.将质量相关的切片能量对 η 进行积分,则软体机械臂的平动动能为

同理,软体机械臂的转动动能为

则软体机械臂总动能为

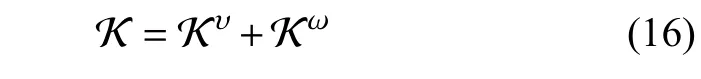
2.1.2 势能计算

软体机械臂的势能主要包括两部分,分别为重力势能和弹性势能,依次进行计算.中性轴上任意点η处切片具有的质量为mdη,则其重力势能为

故整个软体机械臂的重力势能为

式中,g=[0,0,g]T,g表示重力加速度常数.

弹性势能是由于三个驱动器的伸缩效应引起的.驱动器的弹性势能需要根据驱动器所使用的不同的材料建立不同的函数关系[30].一般而言,弹性势能是变形量的函数,即 Pe=f(q) .本文忽略驱动器材料的剪切变形,假设驱动器材料是线弹性的,即驱动器的弹性势能正比于伸长量的平方.因此,软体机械臂的刚度矩阵可以写为

从而软体机械臂的弹性势能为

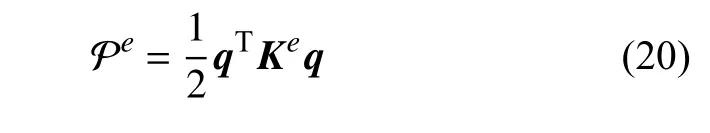
获得以上各能量项后,则软体机械臂的拉格朗日方程为

进而,该软体机械臂驱动关节空间中的拉格朗日动力学方程以矩阵形式表示为

式中,M∈R3×3为机器人的质量矩阵;C∈R3×3为离心力与科里奥利矩阵;G∈R3×3为保守力矢量;Q∈R3×3为外力矢量.

质量矩阵为

保守力矩阵为

2.2 能量分析与方程简化

由于软体机械臂的轴向尺寸远大于其径向尺寸,本节对软体机械臂的平动动能和转动动能进行定量评估.平动动能与转动动能是驱动空间变量q和驱动空间速度的函数,但驱动空间变量受驱动力的影响,随时间变化的规律多样,导致是变化多样的,尽管q与变化规律不定,但受到材料物理极限的限制,两者的变化量必位于某一范围内.假定软体机械臂驱动器的长度变化范围为 [0,30 mm],并且其速度变化范围为 [-50,50 mm/s],在此条件下,通过使用全局搜索计算得到 0≤Kω/K ≤3% .

进而,采用一具体的数值算例对动能进行分析,以便直观的揭示转动动能 Kω占总动能 K 的比值.假定软体机械臂的三个驱动器长度变化量随时间变化规律为,0≤t≤2π,根据驱动器的变化规律,首先计算软体机械臂末端的线速度与角速度,分别如图7 和图8 所示.

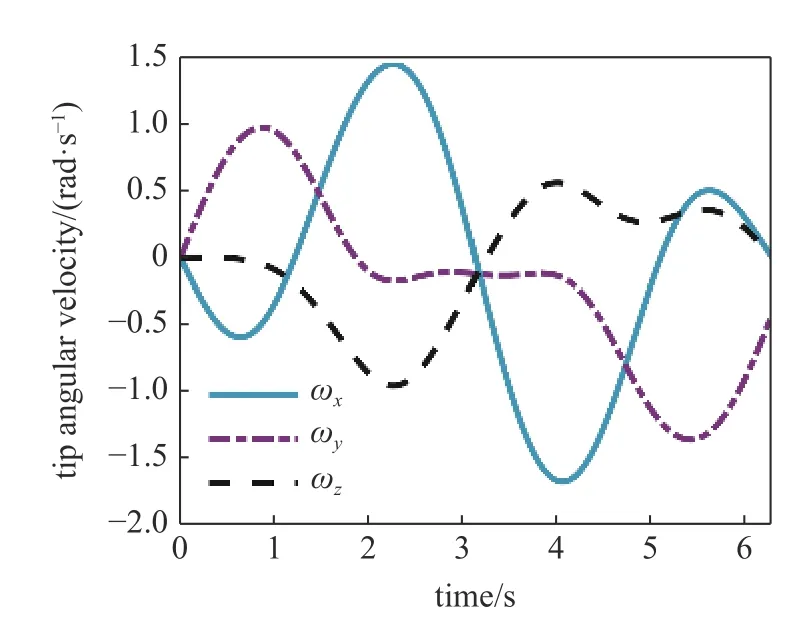
图8 角速度变化曲线Fig.8 Angular velocity

由图7 可以看出线速度的大小为每秒几十毫米,角速度的大小为1 rad/s 左右,这显然符合正常的速度值范围,因此无法通过线速度与角速度的大小关系来判断平动动能和转动动能的大小关系.值得注意的是,在推导二者表达式时得到软体机械臂的平移质量矩阵为 Mυ=mI3,转动质量矩阵为Mω=,两者的数量级是不同的,进而可以定性的判定出平动动能要远大于转动动能.

图7 线速度变化曲线Fig.7 Linear speed

进一步经定量计算得到二者随时间的变化规律如图9 所示,为 Kω和 Kυ随时间变化曲线,从图9 中可以直观地看出转动动能远小于平动动能.如图10所示为 Kω占总动能 K 的比值随时间的变化图,可以发现两者比值最大值不足 1.2%,由此可见,转动动能Kω占总动能 K 的比值很小.另外,根据式(11)和式(12)可以看出,角速度雅可比Jω的计算量要比线速度雅可比Jυ的计算复杂的多,然而其对整个动能的占比又非常小,因此为了简化计算,在建模过程中转动动能可以忽略不计.本文下述动力学分析过程中,均不考虑转动动能,即 K≈Kυ.

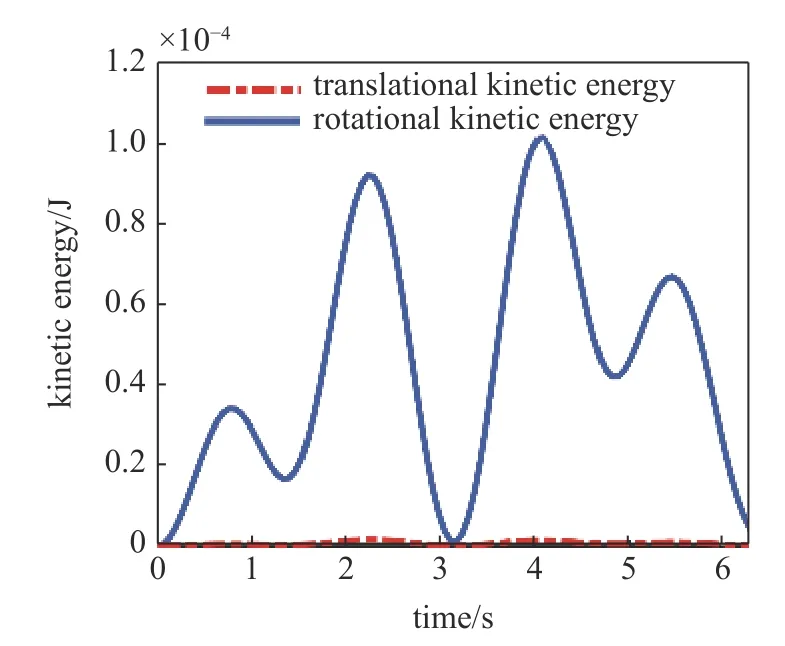
图9 动能变化曲线Fig.9 Kinetic energy

图10 转动动能占总动能百分比Fig.10 Percentage of rotational kinetic energy

如图11 所示为软体机械臂的弹性势能以及重力势能随时间的变化规律.初始时,软体机械臂处于未致动状态,此时三个驱动器的长度均未发生变化,因此弹性势能为零.但重力势能恰好为mgℓ/2=0.112 5 J,随着驱动器长度的变化,重力势能的变化范围并未出现较大的波动,这是因为软体机械臂的质心位置在Z 轴方向上的位移没有发生太大变化,该现象从图12 也能明显发现.弹性势能的变化范围较大,这主要是驱动器长度变化范围引起的.需要特别指出的是,弹性势能与重力势能的大小在同一数量级上,这一点不同于平动动能和转动动能,因此,二者均需要在动力学方程中考虑.

图11 势能比较Fig.11 Potential energy comparison

图12 质心轨迹Fig.12 Trajectory of mass center

通过以上对软体机械臂能量进行计算分析得出如下结论:第一,平动动能远远大于转动动能,因此在动力学方程中忽略转动动能;第二,重力势能与弹性势能处于同一数量级,二者均要在动力学方程中考虑.

2.3 基于质心集中质量动力学建模

考虑基于质心集中质量的动力学模型,质心在动力学分析中具有重要的地位,特别是在刚体力学中,其地位显得尤为重要.事实上在处理大变形问题时,也可以基于质心进行分析,在软体机械臂建模方面,已经提出了许多集中参数模型.然而,近似软体机械臂的平滑弯曲需要将其划分成很多小段或集中质量点,这显著增加了模型的自由度和计算的复杂性[31],迄今为止,集中质量建模研究的重点主要是降低计算复杂性,而没有充分考虑各种近似值在能量域中是否具有良好的匹配精度.本小节将从能量的角度考虑软体机器臂动力学,将集中质量放置在与机械臂的能量行为相匹配的位置(即质心位置).与将集中质量放置在任意位置(例如每个部分的尖端)的集中质量模型相比,基于质心集中质量的动力学模型更接近基于分布质量建立的动力学模型,且没有积分项,计算效率高,并且数值稳定.

2.3.1 基于质心的集中质量动力学建模

基于质心集中质量模型对软体机械臂进行动力学分析,随着驱动器长度的变化,软体机械臂在运动时,其构型时刻发生改变,导致其质心位置不断发生改变,并且软体机械臂在运动过程中,其质心位置不一定位于几何体上.图12 显示了随着机械臂的构型发生变化,其质心的位置也在不断改变.

尽管质心的位置在不断变化,但可以确定的是,软体机械臂质心位置矢量 β∈R3×3必然是驱动空间q的函数,且具有如下表达式

上式对时间求导可得质心的速度为

式中,Jβ表示速度雅可比矩阵且具有如下表达式

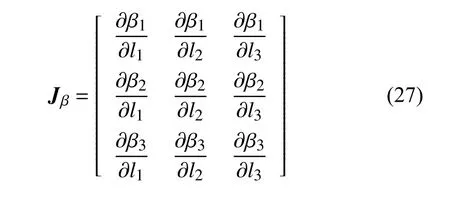
因此基于质心的动能为

同理,基于质心的重力势能为

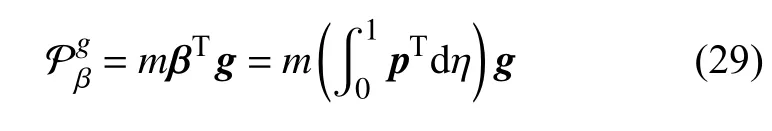
对比式(18)与式(29),不难发现基于质心集中质量模型所求软体机械臂的重力势能和采用连续分布质量所求的动力学模型相等.进一步分析基于质心所求的软体机械臂的动能 Kβ与采用连续分布质量积分所求的动能 K,显然,两种方式计算出的动能都是驱动空间变量q以及其导数的函数,但驱动空间受驱动力的影响,其随时间变化的规律是不确定的,将影响的变化,尽管其变化规律不定,但受到物理极限的限制,两者的变化必定位于某一范围内.为了比较 Kβ与 K 的数量关系,现假定两者的变化范围为[0,30 mm],[-50,50 mm/s],在该范围内随机生成10 000 个数据点来比较两者的数量关系,结果如图13 所示.

图13 随机样本下动能大小Fig.13 Kinetic energy under a random sample

显然两者的大小并不相等.进一步研究两者的比值关系,即对每一个随机数据点计算,计算结果如图14 所示,由图发现比值的范围落在区间 [0.5,0.75] 内,并且大致以0.56 为中心上下波动.将区间 [0.5,0.75] 以0.05 为间隔划分为五个子区间,对随机生成的10 000 个数据点落在各区间的数量进行统计,统计结果见表1.

表1 样本点落入各区间的个数Table 1 The number of sample points falling into each interval

图14 动能等效系数Fig.14 Kinetic energy equivalent coefficient

计算落在每个子区间的概率,绘制成如图15 所示的条形图,由图15 可知,落在0.5 到0.6 之间的概率约为 93% ,均值记为 ξ,计算结果为 ξ=0.56 .

图15 概率条形图Fig.15 Probability bar

接着,以积分动能 K 为横坐标,以质心动能Kβ为纵坐标绘制散点图,如图16 所示,显然散点数据大致散落在某直线附近,然后对数据进行最小二乘拟合,拟合结果为一条过原点的直线,从上面的分析可以看出该直线斜率的物理意义即为 ξ .

图16 积分动能与质心动能比值关系拟合曲线Fig.16 Fitting curve of the ratio between integral kinetic energy and center-of-mass kinetic energy

由此可见将软体机械臂的质量等效为位于质心处的集中质量所计算得到的质心动能 Kβ与实际的连续分布质量所计算得到的积分动能 K 是不相等的,但是二者的比值近似为一定值 ξ,将该定值称为动能等效系数,为了补偿二者的不等,引入基于质心的等效质量mβ,并且使mβ=m/ξ,如此,便可近似认为 Kβ≈K,从而使得基于质心所得的动能在能量上与分布式积分方法所得动能匹配起来.

综上分析,基于质心集中质量模型的软体机械臂拉格朗日函数为 Lβ=Kβ-Pβ,其中 Kβ由式(28)得到,.最终,将软体机械臂的质量等效为位于质心的集中质量模型的动力学方程以矩阵形式可以写为

3 数值仿真算例

本小节对上述建立的软体机械臂动力学模型进行数值仿真分析,动力学仿真参数参考文献[32],如表2 所示.

表2 动力学仿真数值Table 2 Parameters used in the dynamic simulation

3.1 纯伸长模拟

图17 驱动器长度变化曲线Fig.17 Actuator length

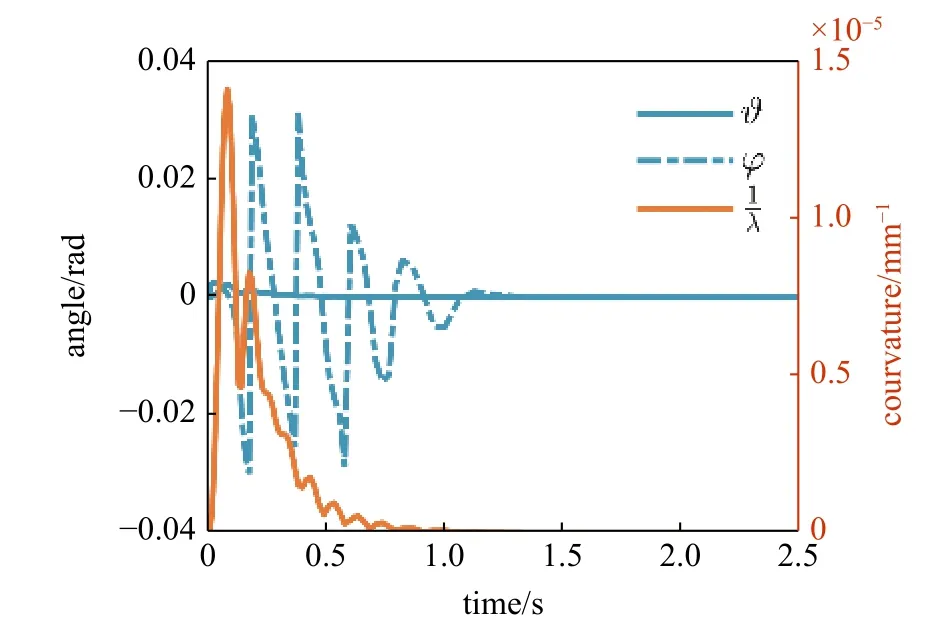
图18 配置空间变量变化曲线Fig.18 Configure space variables

3.2 计算效率比较

为了定量比较动力学建模过程使用的两种方法(即采用分布质量建立的积分动力学模型以及将质量等效成位于软体机械臂质心的集中质量动力学模型)的数值计算结果与计算效率,对相同输入条件下两种动力学模型的求解结果以及数值仿真时间进行比较.图19 表示的是采用分布质量的积分动力学模型求得的结果,图20 是采用基于质心的集中质量动力学模型所求结果,比较图19 和图20,可以发现二者的求解结果一致,但使用两种方法所用的时间却大不相同,表3 给出了相同条件下两种动力学模型的计算时间,结果表明基于质心的集中质量模型的求解效率比分布质量模型提高了大约8 倍.

表3 两种动力学模型的计算效率比较Table 3 Comparison of computational efficiency of the two models

图19 分布质量模型响应曲线Fig.19 Responses from distributed mass model

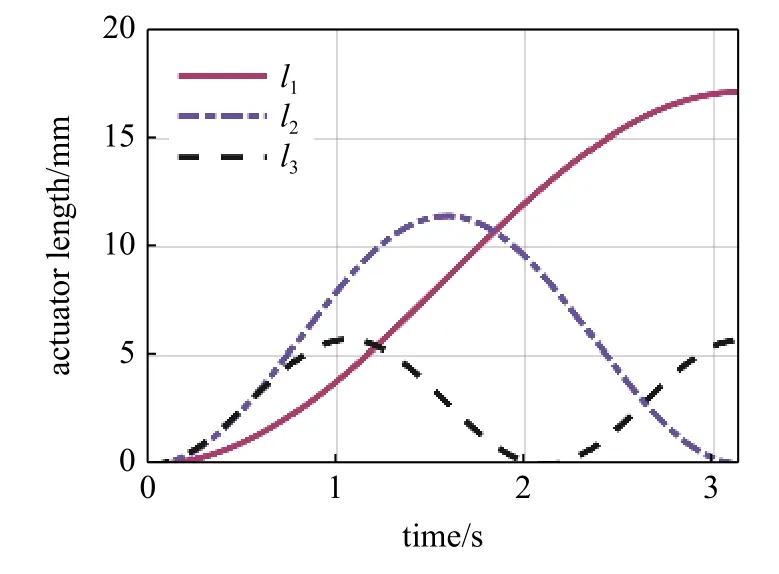
图20 基于质心的集中质量模型响应曲线Fig.20 Responses from concentrated mass model based on mass center

分析其原因在于本文所提出的基于质心集中质量动力学模型的主要优点是它不需要可积项乘积的预积分.例如,式(14)必须预先通过对中性轴上任意点对位置求导得到速度雅可比矩阵Jυ,而该矩阵是含有积分变量η的函数矩阵,这必然会导致(Jυ)TJυ是关于积分变量η更加复杂的矩阵,然后对η积分后才能得到动能.与之相反的是,使用基于质心的集中质量模型恰好避免了这一复杂的积分计算,这是因为式(25)是预先对积分变量η进行积分,显然这一步的积分运算是简单的,其后再求速度并计算动能,显著降低了计算的复杂性.

4 结论

本文以一类具有常曲率弯曲与伸长能力的软体机械臂为研究对象,对其空间运动学及动力学建模与仿真进行了研究,主要研究结论如下.

(1) 本文采用模态方法对软体机械臂进行运动学描述,该方法以多项式函数描述软体机械臂的变形场,能够简便地推导出精确、无奇异且唯一的模态变换矩阵,该方法在没有使用中间变换或曲线参数的情况下,直接以驱动关节变量推导软体机械臂运动学方程.仿真结果表明该方法既能有效模拟软体机械臂的弯曲行为,又可以模拟软体机械臂的纯伸长运动,不需要将纯伸长运动状态单独考虑,有效克服了以往模型假定软体机械臂变形后曲率不为零(只能模拟弯曲变形,而不能模拟直线运动)的局限性.

(2) 软体机械臂动力学建模时,转动动能计算复杂,影响动力学方程的求解效率,但与平动动能相比,在给定条件下,转动动能占总动能的百分比不超过3%,其对动力学结果影响很小.因此在动力学建模过程中可以忽略,进而提高动力学方程求解效率,为软体机械臂的实时动态控制奠定了理论基础.

(3) 本文提出的基于质心集中质量动力学模型,将软体机械臂的连续分布质量模型等效为位于质心的集中质量模型,利用统计的方法计算出动能等效系数,进而通过动能等效系数实现两种模型的动能匹配.仿真结果表明,本文所建立的模型既具有分布质量模型的准确性,又具有集中质量模型的计算高效性,能够准确、高效地获得软体机械臂的动力学特性.