基于沪深300ETF的期权定价实证研究

陈乐川 刘文文 何江

摘 要：本文以沪深300ETF为研究对象，利用沪深300ETF的日收盘价和沪深300ETF期权合约数据，检验沪深300ETF的对数日收盘价的正态性。根据B-S模型进行定价。由于B-S模型中波动率为常数，与现实市场观测到的“波动率微笑”曲线不符，故引入heston模型进行定价。对于heston模型中需要确定的5个参数，采用模拟退火算法进行估算，比较B-S模型及heston模型对于看涨期权和看跌期权的定价效果。从而对B-S模型的假设和局限性进行分析，最终得到结论：沪深300ETF对数收盘价不服从正态分布，B-S模型中第2个假设条件——股票对数价格符合正态分布不成立。B-S模型能较好地对沪深300ETF期权进行定价，heston模型定价效果优于B-S模型，两个模型对看涨期权的定价效果均优于看跌期权的定价效果，B-S模型中第6个假设条件——股票收益波动率σ为常数并已知不成立。

关键词：B-S模型；heston模型；模拟退火算法

一、引言

近年来我国金融市场发展迅速，大力推动了金融衍生品的产生和发展。在金融活动中，金融衍生工具也逐渐体现其重大价值。在金融衍生品中，期权具有独特的功能和用途。而研究期权定价，无论出于套期保值或者投机套利等目的都具有现实意义。由于我国金融发展起步较晚，市场尚未成熟，具体表现为市场中投机氛围较重，股市横盘震荡趋势明显，股票涨跌的不确定性较高，导致金融资产价格波动较大，投资者面临的风险较大，可能會造成损失。此时，利用期权构建投资组合，对冲风险，稳定收益，则十分重要。因此本文研究期权定价问题，具有现实参考价值。

期权定价一直是金融界的研究热点，许多学者对其进行了深入研究。宋海明和侯頔基于Black-Schole模型， 设计一种针对该模型的神经网络算法，并给出美式期权价格的数值近似，通过对比二叉树方法，证明该算法的有效性。于长福和陈婷婷使用上证50ETF的历史波动率作为其期望波动率，并使用B-S模型对上证50ETF期权进行定价。方艳、张元玺和乔明哲没有直接使用历史波动率，而是使用IGARCH模型和GARCH模型分别预测上证50ETF的波动率，将其作为期望波动率，并用蒙特卡罗法和B-S模型分别对上证50EFT期权定价。通过对比后发现，IGARCH模型对上证50ETF波动率的预测效果优于GARCH模型；当模拟次数大于1000时，蒙特卡罗法对上证50ETF期权定价效果略优于B-S模型。然而无论是用历史波动率还是预测波动率来作为期望波动率，都是将期望波动率视为常数。基于这种局限性，邓国和将波动率视为时变函数，使用heston模型进行期权定价，通过变换和求解特征函数，得出heston模型的期权定价公式。由于heston模型需要确定的参数较多，且无法直接求解，王林、张蕾和刘连峰采用模拟退火算法来估算heston模型中需要确定的5个参数，解决了heston模型参数求解困难的问题。姚艾嘉等基于VG过程刻画上证 50ETF 期权标的资产对数价格变化情况，对美国股市熔断前后各9支期权数据采用快速分数阶Fourier变换进行期权定价研究，实证表明：VG过程依然拟合较好，用快速分数阶Fourier变换数值方法具有一定优势。而刘莹和郑玉衡使用粒子群（PSO）智能算法估计了heston的6个参数进行期权定价研究，结果表明结合粒子群智能算法估计的heston模型参数进行期权定价效果较好。

本文以沪深300ETF为研究对象，利用沪深300ETF的日收盘价和沪深300ETF期权合约数据，检验沪深300ETF的对数日收盘价的正态性。根据B-S模型和heston模型进行定价，对于heston模型中需要确定的5个参数，采用模拟退火算法进行估算，比较两个模型对于看涨期权和看跌期权的定价效果。从而论证B-S模型的假设在实际市场中不成立，B-S模型具有局限性。

二、理论框架

1B-S模型

若连续随机过程{B（t），t≥0}满足以下性质：

①B（0）=0；

②对s∈［0，t），增量B（t）-B（s）～N（0，t-s）；

③对于不重复的区间［si，ti］，随机变量B（ti）-B（si）之间是相互独立的，则B（t）是一个标准布朗运动。

令ti∈0，T，i=0，1，…，N，并使间隔满足Π={0=t0<t1<t2<…<tN=T}，则对于f（t），有∑N-1i=0［fti+1-f（ti）］2。

对于一个连续且在0到T内处处可微的函数f（t），根据微分中值定理得到如下不等式

∑N-1i=0fti+1-fti2≤∑N-1i=0ti+1-ti2f′si2≤maxs∈［0，T］f′s2∑ti+1-ti2≤maxs∈0，Tf′s2maxiti+1-ti2T（1）

将连续可微函数f（t）替换为布朗运动B（t），可以看到随着对时间区间［0，T］的细分，maxiti+1-ti2趋近于0，布朗运动B（t）的二次变分为T，即

lim|Π|→0∑iBti+1-Bti2=T（2）

其中

Π=maxiti+1-ti2（3）

二次变分用无穷小量形式可以表示为（dB）2=dt。

给标准布朗运动加上一个仅和时间t有关的漂移项μt以及一个尺度参考σ，得到带漂移项的布朗运动，记作X（t）=μt+σB（t）。其满足X（t）～Nμt，σ2t，t≥0。若时间t为无穷小量，则上式可改写为

dX（t）=μdt+σdB（t）（4）

用X（t）表示股票的收益率，则令S（t）为股票价格，dS（t）为股票价格在微小间隔的变化量St+Δt-S（t），所以

dX（t）=dS（t）S（t）=μdt+σdB（t）（5）

因此，S（t）的随机微分方程为

dS（t）=μS（t）dt+σS（t）dB（t）（6）

上式表示股价S（t）满足几何布朗运动。令f（Bt）为布朗运动Bt的连续平滑函数，根据泰勒公式，有

fx+Δx=f（x）=f′（x）Δx+f″（x）2！（Δx）2+f（x）3！（Δx）3+…（7）

将x=Bt代入上式，得到

Δf（Bt）=fBt+ΔBt-f（Bt）=f′（Bt）ΔBt+f″（Bt）2！ΔBt2+f（Bt）3！（ΔBt）3+…（8）

因為（dB）2=dt，利用无穷小量形式忽略等式右边第三项开始之后的所有项，得到伊藤引理最基本形式

df（Bt）=f′（Bt）dBt+f″（Bt）2！dt（9）

由全微分公式可以得到

df=ftdt+fxdx（10）

把x=Bt代入上式，得到伊藤微积分

df=ftdt+fxdBt+122fx2（dBt）2

=ft+122fx2dt+fxdBt（11）

对于带有漂移项的布朗运动dX（t）=μdt+σdB（t），令a（X（t），t）和b（X（t），t）表示漂移和扩散系数，即aX（t），t=μ，bX（t），t=σ，则称如下随机微分方程（SDE）为伊藤漂移扩散过程。

令连续函数f（X（t），t）满足X（t）二阶可导，t一阶可导，得到

df=ftdt+fxdx+122fx2（dx）2（12）

将dX（t）=aX（t），tdt+bX（t），tdB（t）代入上式，得伊藤引理一般形式

df=ft+fxa+122fx2b2dt+fxbdB（t）（13）

对于股票价格S，满足dS（t）=μS（t）dt+σS（t）dB（t），此时布朗运动的漂移系数a=μS，扩散系数b=σS。令f=lnS，则伊藤引理一般形式为

df=d（lnS）=ft+fSa+122fS2b2dt+fSbdB（t）=μ-σ22dt+σdB（14）

将等式两边同时取积分，得到

∫T0d（lnS（t））=∫T0μ-σ22dt+∫T0σdB（t）（15）

lnS（T）S（0）=μ-σ22T+σB（T）（16）

S（T）=S（0）eμ-σ22T+σB（T）（17）

由于s∈［0，t），增量B（t）-B（s）～N（0，t-s）。当s=0时，Bs=0，有B（t）～N（0，t），B（t） t～N（0，1）。所以上式可以变为

S（T）=S（0）eμ-σ22T+σ Tε（18）

其中，S（0）表示初始时刻股票价格；μ为股票期望收益率；σ为股票期望收益率波动率；T表示经历的时间；ε服从标准正态分布，S（T）表示T时刻股票价格。

根据下列假设条件：

①期权合约是欧式期权；

②股票对数价格符合正态分布；

③允许做空证券，且证券可以被分割；

④市场无摩擦，不存在交易费用和税收；

⑤标的股票不支付股息；

⑥股票收益波动率σ为常数并已知；

⑦市场不存在无风险套利机会；

⑧股票交易连续；

⑨短期无风险利率r为常数并已知。

令CS，t表示由标的股票价格S和距离期权到期日的时间t所确定的欧式看涨期权的价格，简记为C。根据下式

df=ft+fSa+122fS2b2dt+

fSbdB（t）（19）

将f替换为C，由a=μS和b=σS得到

dC=CSμS+Ct+122CS2σ2S2dt+

CSσSdB（20）

将S，C，B，t离散化，即dC=ΔC，dB=ΔB，dS=ΔS，dt=Δt，得到

ΔC=CSμS+Ct+122CS2σ2S2Δt+

CSσSΔB（21）

ΔS=μS（t）Δt+σSΔB（22）

不难看出，ΔC和ΔS的表达式都含有布朗运动ΔB，所以同时做空1份期权，做多CS份股票，可以将ΔB完美对冲，用P表示该投资组合的价值，则在时间Δt内的变化为

ΔP=CSΔS-ΔC=

（-Ct-122CS2σ2S2）Δt（23）

因为该投资组合消除了全部风险，所以组合在Δt内收益为无风利率r，即ΔP=rpΔt。将ΔP和P=CSS-C代入上式可以得到：

Ct+rSCS+122CS2σ2S2=rC（24）

解偏微分方程得到B-S期权定价公式：

C=S（0）Nd1-Ke-rTN（d2）（25）

d1=lnS（0）K+r+σ22Tσ T（26）

d2=lnS（0）K+r-σ22Tσ T=

d1-σ T（27）

其中，C表示看涨期权的理论价格；S（0）表示标的资产当期价格；K表示看涨期权的行权价格；σ表示标的资产的年收益率波动率；T表示当前时间距离期权到期日的天数（按年计算）；r表示无风险利率；N表示标准正态分布累积密度函数。同理可以得到看跌期权的理论价格P

P=Ke-rTN-d2-S（0）N-d1（28）

2heston模型

由于上文中B-S模型的第6个假设条件：在期权期限内，标的股票年收益率的标准差σ为常数并已知，明显与现实市场观测到的“波动率微笑”曲线严重不符。且B-S模型的第5个假设条件：在期权期限内，标的股票不支付股息，也常常与现实市场不符，所以基于B-S模型进行改进。

假设t时刻的股票价格St和波动率vt服从几何布朗运动：

dSt=（r-q）Stdt+ vtStdW1t（29）

dvt=κ（θ-vt）dt+δ vtdW2t（30）

其中，q表示股票连续支付的红利率；v是一个不可观测的状态变量，满足均值回复平方根CIR過程；参数κ，θ，δ为非负常数。求解得出heston定价公式：

Cet，T，St，vt，K=Ste-q（T-t）P1-

Ke-rT-tP2（31）

Pj=12+1/π∫+SymboleB@

0Re［e-ilnKfj（x，v，τ;）i］d， j=1，2

（32）

fj（x，v，τ;）=exp［A（τ;）+B（τ;）v+ix］，   j=1， 2（33）

x=lnS（34）

A（τ;）=irτ+aδ2［（bj-ρδi+hj）τ-

2ln （1-gjehjτ1-gj）］（35）

Bτ;=bj-ρδi+hjδ2（1-ehjτ1-gjehjτ）］（36）

gj=bj-ρδi+hjbj-ρδi-hj（37）

hj= （ρδi-bj）2-δ2（2uji-2）（38）

其中，u1=1/2；u2=-1/2；a=κθ；b1=κ-ρδ；b2=κ；j=1，2；Re表示被积函数的实数部分，i为虚数单位；Cet，T，St，vt，K为欧式看涨期权的理论价格。根据平价公式可以得出，欧式看跌期权的理论价格为

Pet，T，St，vt，K=Cet，T，St，vt，K+

Ke-rT-t-Ste-q（T-t）（39）

由于本文研究的是滬深300ETF期权，没有红利，所以令q=0，即认为B-S模型中第5个假设成立。重点论证B-S模型中第2个假设条件和第6个假设条件是否在市场中成立。

三、实证分析

1数据来源及处理

本文选取沪深300ETF和华泰柏瑞沪深300ETF期权进行研究。时间上，本文选取从2020年1月1日到2020年12月31日的交易日数据，共有243个交易日。选择该区间的原因是在这段时间里，由于新冠肺炎疫情的影响，从2020年上半年的悲观消极到下半年的复工复产，沪深300ETF经历了大涨和大跌，横穿牛熊市，囊括了大盘周期，且数据比较新。标的物上，本文选取沪深300ETF在这243个交易日的日线行情数据，包括收盘价、收益率等；在期权合约方面，本文按照以下三个条件筛选出满足条件的期权合约数据进行研究。

（1）对于期权到期日距当前不足6个交易日的期权合约，由于这类合约包含的时间价值较少，价格波动较大，所以剔除这类合约。对于期权到期日距当前超过60个交易日的期权合约，由于这类合约流动性差，成交量少，所以剔除这类合约。

（2）对于执行价与当前价格相差两个价位（如交易平台的买三和买一）的期权合约，由于这类期权合约大多数为深度实值期权或深度虚值期权，成交量少，所以剔除这类合约。

（3）根据看涨期权和看跌期权的边界条件：

Ct≥max（St-Ke-rt，0）（40）

Pt≥max（Ke-rt-St，0）（41）

所以剔除不满足边界条件的期权合约，最终通过筛选得到沪深300ETF期权数据共4348条，其中看涨期权和看跌期权数据各2174条。本文全部数据均来源于tushare。

2正态性检验

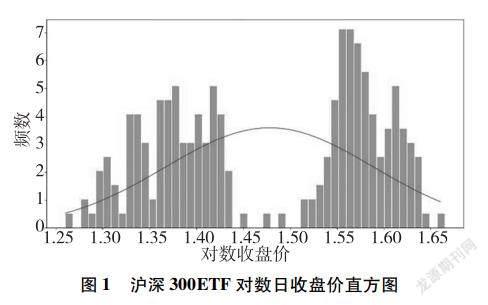
首先对沪深300ETF对数日收盘价的正态性进行分析，检验B-S公式第2个假设条件是否成立，结果如图1、图2和表1所示。

由图1和图2可以初步判断，沪深300ETF的对数收盘价不服从正态分布。根据图1所示，沪深300ETF的对数收盘价呈现中间低、两边高的现象，对数收盘价总体聚集在137和157附近，而中间145到15极少。根据图2所示，散点的分布除了少部分与直线重合外，大部分都偏离直线。表1是具体计算得到的结果。由表1可以看到，沪深300ETF的对数收盘价偏度是负的，说明左边是拖尾的；峰度为负数，与正态分布的峰度3相差很大；由于样本量仅为243个，所以选择Shapiro-Wilks检验其正态性，得到检验统计量为0181，检验p值为0，小于显著性水平005，拒绝其服从正态分布的检验。因此可以说明，沪深300ETF的对数收盘价不服从正态分布，即B-S公式第2个假设条件在实际市场中是不成立的。

3B-S模型定价效果

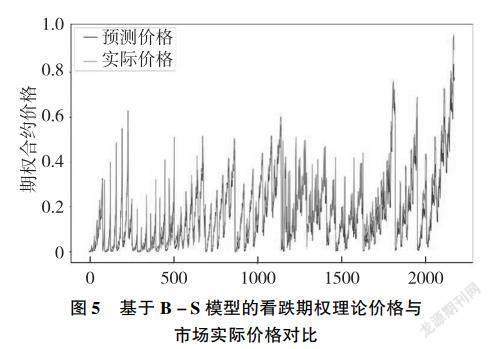
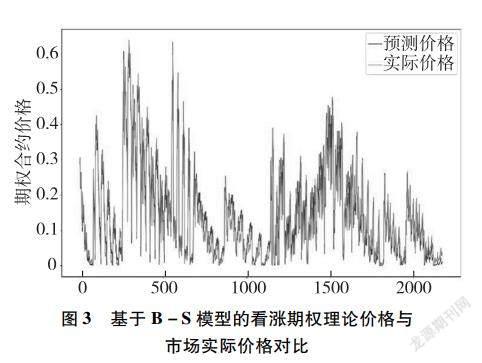
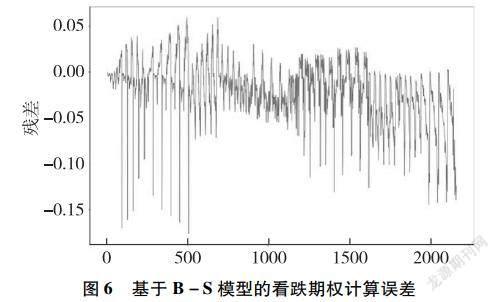
为了方便计算，我们设定B-S公式中无风险利率r为4%。将沪深300ETF 30日收益率标准差转化为年标准差，即波动率σ。对沪深300ETF看涨期权合约和看跌期权合约分别进行定价，得到结果如图3至图6所示。

由图3至图6可以看出，基于B-S模型的残差较小，曲线拟合效果较好。总体来看，基于B-S模型对看涨期权和看跌期权定价是可行的。

4heston模型定价效果

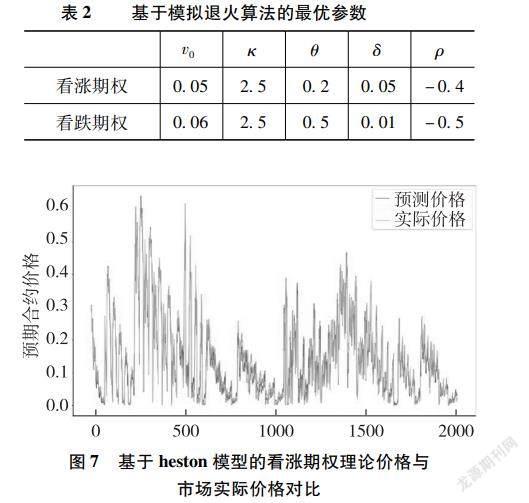
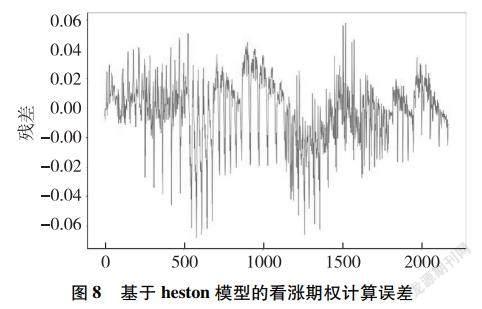
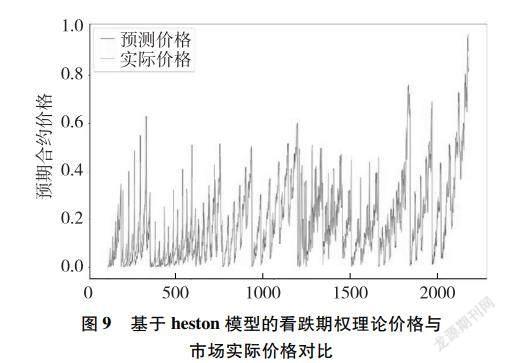
根据前文所述内容，由于heston模型的看涨期权价格公式和看跌期权价格公式比较复杂，无法通过直接求导，即令导数为0的方法来求解非线性最小二乘问题，只能用其他优化算法求得局部极小值。模拟退火算法是一种随机寻优算法，其基本思想是：设定初始温度和初始状态，通过内循环迭代，以Metropolis准则更新状态，得到稳定状态后根据快速降温公式降温，不断迭代直到最后温度低于设定的最低温度，此时稳定状态即为估算结果。相比于遗传算法、混沌算法而言，原理较为简单，易于仿真，且模拟效果好。所以本文采用模拟退火算法估计参数，得到结果如表2所示。根据表2得到的参数和B-S模型中的参数，对沪深300ETF看涨期权合约和看跌期权合约分别进行定价，得到结果如图7至图10所示。

由图7至图10可以看出，基于heston模型的残差较小，曲线拟合效果较好。总体来看，基于heston模型对看涨期权和看跌期权定价是可行的。

5两个模型定价效果对比

为了直观比较基于B-S模型和基于heston模型对看涨期权和看跌期权的定价效果，本文构建绝对平均误差MAE和均平方根误差RMSE这两个指标评估模型定价效果，结果如表3和表4所示。

MAE=∑Mi=1|ki-wi|M（42）

RMSE= ∑Mi=1（ki-wi）2M（43）

其中，ki表示模型预测数据；wi表示市场真实数据；M表示样本量。绝对平均误差MAE和均方根误差RMSE越小，表示模型预测效果越好；反之则反。

由表3和表4可以看出，heston模型对看涨期权和看跌期权的定价效果均优于B-S模型，说明将波动率视为时变函数优于视为常数，B-S模型中第6个假设条件不成立。B-S模型和heston模型对于看涨期权的定价效果优于对看跌期权的定价效果。总体而言，B-S模型和heston模型能较好地对看涨期权和看跌期权进行定价。

四、结论

本文以沪深300ETF为研究对象，利用沪深300ETF的日收盤价和沪深300ETF期权合约数据，检验沪深300ETF的对数日收盘价的正态性。根据B-S模型和heston模型进行定价，对于heston模型中需要确定的5个参数，采用模拟退火算法进行估算，比较两个模型对于看涨期权和看跌期权的定价效果。得到结论：沪深300ETF对数收盘价不服从正态分布，B-S模型中第2个假设条件不成立。B-S模型能较好地对沪深300ETF期权进行定价，heston模型定价效果优于B-S模型，两个模型对看涨期权的定价效果均优于看跌期权的定价效果，B-S模型中第6个假设条件不成立。

本文由于篇幅有限，仅对B-S模型中两个假设条件进行论证。实际上，B-S模型的其他假设条件在真实市场中也具有局限性，可以进行扩展研究。此外，本文研究的是平值期权，对于深度实值或深度虚值期权，B-S模型和heston模型定价效果可能较为一般。

参考文献

［1］潘军昌， 陶钧 股票市场投机资本运作现状探析［J］ 西安财经学院学报， 2015， 28（2）：19-22

［2］宋海明， 侯頔 Black-Scholes模型下美式期权定价的神经网络算法［J］ 吉林大学学报（理学版），2021， 59（5）：1089-1092

［3］于长福，陈婷婷基于B-S模型的上证50ETF期权定价的实证研究［J］金融理论与教学，2016（2）：7-11

［4］方艳，张元玺，乔明哲上证50ETF期权定价有效性的研究：基于B-S-M模型和蒙特卡罗模拟［J］运筹与管理，2017，26（8）：157-166

［5］邓国和Heston模型的欧式任选期权定价与对冲策略［J］广西师范大学学报（自然科学版），2012，30（3）：36-43

［6］王林，张蕾，刘连峰用模拟退火算法寻找Heston期权定价模型参数［J］数量经济技术经济研究，2011，28（9）：131-139，153

［7］姚艾嘉， 张艳慧， 李明阳，等 基于快速分数阶Fourier变换的期权定价——以上证50ETF期权为例［J］ 江西师范大学学报（自然科学版），2020， 44（6）：614-620

［8］刘莹， 郑玉衡 使用粒子群算法解决期权定价模型参数校准问题——以heston模型为例［J］ 科学决策， 2019（12）：34-46

［9］BLACK F，SCHOLES MSThe Pricing of Options and Corporate Liabilities［J］ Journal of Political Economy， 1973， 81（3）：637-654

［10］HESTON S L A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options［J］ Review of Financial Studies， 1993，6（2）：327-343

Empirical Research on Option Pricing Based on CSI 300 ETF

CHEN Lechuan LIU Wenwen HE Jiang

Abstract：This paper takes the CSI 300 ETF as the research object， and uses the daily closing price of the CSI 300 ETF and the CSI 300 ETF option contract data to test the normality of the log-day closing price of the CSI 300 ETF Pricing is based on the B-S model Since the volatility in the B-S model is constant， which is inconsistent with the“volatility smile”curve observed in the real market， the heston model is introduced for pricing For the five parameters that need to be determined in the heston model， the simulated annealing algorithm is used to estimate， and the pricing effects of the B-S model and the heston model for call options and put options are compared Therefore， the assumptions and limitations of the B-S model are analyzed， and the final conclusion is drawn： the logarithmic closing price of the CSI 300 ETF does not follow the normal distribution， and the second assumption in the B-S model， the log price of stocks， does not conform to the normal distribution. The B-S model can price CSI 300 ETF options better， the heston model has a better pricing effect than the B-S model， the pricing effect of both models on call options is better than the pricing effect of put options， and the sixth assumption in the B-S model， stock return volatility σ is constant and is known to be invalid

Keywords：B-S Model；Heston Model；Simulated Annealing Algorithm